На рисунке изображён график функции $y=f(x)$, определённой на интервале $(-4;10)$. Найдите количество решений уравнения $f'(x)=0$ на интервале $(-4;3)$.
Так как угловой коэффициент касательной $k = tg α = f′(x_0) = 0$, то это означает, что касательная к графику данной функции параллельна оси абсцисс.
На интервале $(-4; 3)$ построены три касательные, параллельные оси абсцисс.
Видео:✓Дифференцируемая функция. Дифференциал | матан #032 | Борис ТрушинСкачать
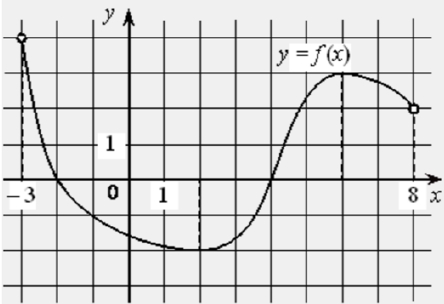
Решение №1891 На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (-3;8).
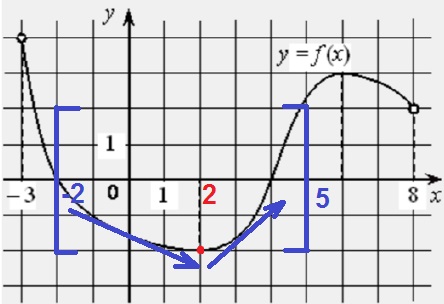
На рисунке изображён график дифференцируемой функции 𝑦 = 𝑓(𝑥), определённой на интервале (−3;8). Найдите точку из отрезка [−2;5], в которой производная функции 𝑓(𝑥) равна 0.
Производная функции 𝑓(𝑥) равна 0 в точках максимума или минимума, на отрезке [−2;5], одна такая точка х = 2 .
Ответ: 2.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Видео:Задание 7 ЕГЭ по математикеСкачать
Задание 6 ЕГЭ по математике (профиль)
Открытый банк заданий mathege.ru — тренажер задания 6 профильного ЕГЭ по математике-2022 (с ответами). Все прототипы задания 6 на исследование функций. Это задание на использование свойств производной при анализе функций, либо на геометрический смысл производной, либо на физический смысл производной, либо на первообразную функции. Номер заданий соответствует номеру заданий в базе mathege.ru.
Видео:Задача 7 ЕГЭ по математике #5Скачать
Использование свойств производной для исследования функций
27487 На рисунке изображен график функции y = f(x), определенной на интервале (-6; 8). Определите количество целых точек, в которых производная функции положительна.
27488. На рисунке изображён график функции y = f(x), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции отрицательна.
27490. На рисунке изображен график функции y = f(x), определенной на интервале (-2; 12). Найдите сумму точек экстремума функции f(x).
27491. На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 3). В какой точке отрезка [-3; 2] функция f(x) принимает наибольшее значение?
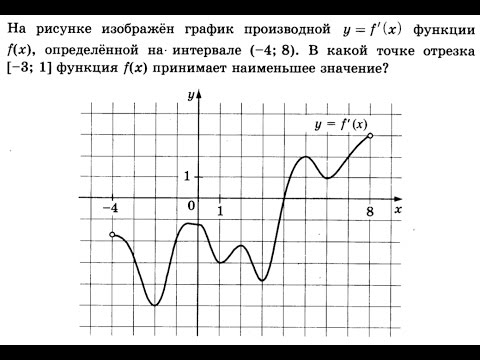
27492. На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 4). В какой точке отрезка [-7;-3] функция f(x) принимает наименьшее значение?
27494. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6;9].
27495. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-18; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-13;1].
27496. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-11; 11). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-10;10].
27497. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
27498. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
27499. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
27500. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
27502. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-4; 8). Найдите точку экстремума функции f(x), принадлежащую отрезку [-2; 6 ].
119971. На рисунке изображен график функции f(x), определенной на интервале (-5;5). Найдите количество точек, в которых производная функции f(x) равна 0.
317539. На рисунке изображён график функции y = f(x) и восемь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек производная функции f(x) положительна?
317540. На рисунке изображён график функции y = f(x) и двенадцать точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12. В скольких из этих точек производная функции f(x) отрицательна?
317541. На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек лежит на промежутках возрастания функции f(x)?
317542. На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек лежит на промежутках убывания функции f(x)?
Видео:Производные, номер 13.1, ЕГЭ по профильной математике.Скачать
Геометрический смысл производной
27485. Прямая y = 7x — 5 параллельна касательной к графику функции y = x 2 + 6x — 8. Найдите абсциссу точки касания.
27486. Прямая y = -4x — 11 является касательной к графику функции y = x 3 + 7x 2 + 7x — 6. Найдите абсциссу точки касания.
27489. На рисунке изображен график функции y = f(x), определенной на интервале (-5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
27501. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = -2x -11 или совпадает с ней.
27503. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
27504. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
27505. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
27506. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
40130. На рисунке изображен график y = f'(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 2x — 2 или совпадает с ней.
40131. На рисунке изображен график y = f'(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна оси абсцисс или совпадает с ней.
119972. Прямая y = 3x +1 является касательной к графику функции ax 2 + 2x + 3. Найдите a.
119973. Прямая y = -5x + 8 является касательной к графику функции 28x 2 + bx + 15. Найдите b, учитывая, что абсцисса точки касания больше 0.
119974. Прямая y = 3x + 4 является касательной к графику функции 3x 2 — 3x + c. Найдите c.
317543. На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
317544. На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
[s60u_expand more_text=»Ответ» less_text=»Свернуть» height=»1″ hide_less=»no» text_color=»#333333″ link_color=»#0088FF» link_style=»default» link_align=»left» more_icon=»» less_icon=»» /> [/su_expand]
Видео:Все Задания 8 ЕГЭ 2024 ПРОФИЛЬ из Банка ФИПИ (Математика Школа Пифагора)Скачать
Физический смысл производной
119975. Материальная точка движется прямолинейно по закону x(t) = 6t 2 — 48t +17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9 с.
119976. Материальная точка движется прямолинейно по закону x(t) = 1/2t 3 — 3t 2 + 2t, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6 с.
119977. Материальная точка движется прямолинейно по закону x(t) = -t 4 + 6t 3 + 5t + 23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3 с.
119978. Материальная точка движется прямолинейно по закону x(t) = t 2 -13t +23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
119979. Материальная точка движется прямолинейно по закону x(t) = 1/3t 3 — 3t 2 — 5t + 3, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Видео:21. Дифференциал функцииСкачать
Первообразная
323077. На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (-3;5). Найдите количество решений уравнения f(x) = 0 на отрезке [-2;4].
323078. На рисунке изображён график функции y = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) — F(2), где F(x) — одна из первообразных функции f(x).
323079. На рисунке изображён график некоторой функции y = f(x). Функция F(x) = x 3 + 30x 2 + 302x — 15/8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
323080. На рисунке изображён график некоторой функции y = f(x). Функция F(x)= -x 3 — 27x 2 — 240x — 8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
🌟 Видео
ЕГЭ 2017 Профильный №7 есть график производной, найти где функция минимальна #7Скачать
Дифференциал функцииСкачать
Профильный ЕГЭ 2023 математика. Производная. Задача 11Скачать
На рисунке изображён график —производной функции определённой на интервале . В какой точке отрезкаСкачать
Производные, номер 23.1, ЕГЭ по профильной математикеСкачать
Задача 7 ЕГЭ по математике #10Скачать
ЕГЭ математика профиль #1.18 задача 7🔴Скачать
Щелчок по математике I №7,11 Производная. Вся теория и решение прототипов ФИПИСкачать
Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать
Все задания №8 (раньше №7) с реального ЕГЭ по профильной математике! Производная на ЕГЭ.Скачать
Производные, номер 15.1, ЕГЭ по профильной математикеСкачать
АЛГЕБРА С НУЛЯ — Точки Экстремума ФункцииСкачать
На рисунке изображен график функции. Найдите количество точек в которых производная функции равна 0.Скачать
ЗАДАНИЕ №7 Производная и графики функции | PARTAСкачать
