Рассмотрим вопрос о зависимости решения задачи Коши от начальных данных. Пусть дана задача Коши
Если функция f(t, х) непрерывна по совокупности аргументов и имеет ограниченную производную 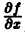

Справедлива следующая теорема о непрерывной зависимости решения от начальных условий.
Теорема:
Если правая часть f(t, х) дифференциального уравнения
непрерывна по совокупности переменных и имеет ограниченную частную производную 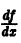
удовлетворяющее начальному условию 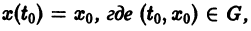
Иными словами, пусть через точку 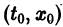
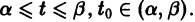
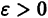
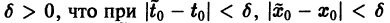
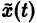
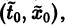
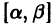
Аналогичная теорема справедлива и для системы дифференциальных уравнений
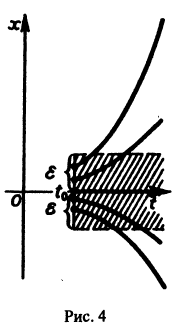
При выполнении условий теоремы (1) решение задачи Коши существует, единственно и непрерывно зависит от начальных данных. В этом случае говорят, что задача Коши поставлена корректно. Существенным является то обстоятельство, что отрезок [а, b] изменения t конечен. Однако во многих задачах нас интересует зависимость решения от начальных данных в бесконечном промежутке 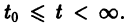
Остановимся вкратце на понятии о продолжаемости решения. Пусть имеем систему дифференциальных уравнений
где t — независимая переменная (время); 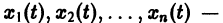
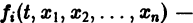
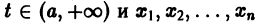
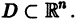
в их области определения непрерывны по совокупности аргументов и имеют ограниченные частные производные по 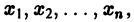
для каждой системы значений
существует единственное решение
системы (3), определенное в некотором интервале 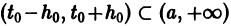
Введем следующее понятие. Пусть
— решение задачи Коши (3)-(4), определенное на некотором интервале I = (t1,t2). Это решение может бьггь продолжено, вообще говоря, на больший интервал времени. Решение
называется продолжением решения 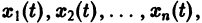
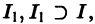
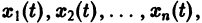
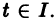
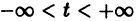
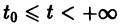
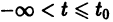
Для дальнейших рассмотрений важен вопрос о существовании решения хi(t), 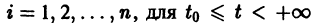
где 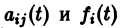
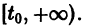
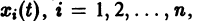
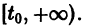
Не все системы обладают таким свойством. Например, для скалярного уравнения
непрерывна и имеет производные всех порядков по х. Нетрудно проверить, что функция
является решением задачи
Однако это решение существует только в интервале 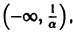
Уравнение (5) есть уравнение сверхбыстрого размножения, когда прирост пропорционален числу всевозможных пар. Его решение показывает, что при таком законе прироста населения количество населения становится бесконечным за конечное время (в то время как обычный закон прироста — экспоненциальный).
Задача:
Показать, что решения уравнения
нельзя продолжить неограниченно ни вправо, ни влево.
- Устойчивость по Ляпунову. Основные понятия и определения
- Устойчивость автономных систем. Простейшие типы точек покоя
- Простейшие типы точек покоя
- Метод функций Ляпунова
- Устойчивость по первому (линейному) приближению
- 23. Нормальные системы линейных однородных дифференциальных
- Обыкновенные дифференциальные уравнения
- Обыкновенные дифференциальные уравнения
- Основные понятия о дифференциальных уравнениях
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения с разделенными переменными
- Дифференциальные уравнения с разделяющимися переменными
- Однородные дифференциальные уравнения
- Линейные дифференциальные уравнения
- Дифференциальное уравнение Бернулли
- Обыновенное дефференциальное уравнение
- Основные понятия и определения
- Примеры с решением
- Системы обыкновенных дифференциальных уравнений
- Системы дифференциальных уравнений первого порядка
- Системы линейных дифференциальных уравнений с постоянными коэффициентами
- 📹 Видео
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Устойчивость по Ляпунову. Основные понятия и определения
Рассмотрим дифференциальное уравнение первого порядка
где функция f(t,x) определена и непрерывна для 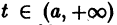
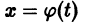
есть решение уравнения (1), удовлетворяющее начальному условию
Пусть, далее, функция
есть решение того же уравнения, удовлетворяющее другому начальному условию
Предполагается, что решения 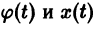
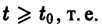
Определение:
Решение 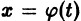
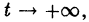
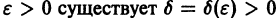
для всех 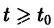
Это значит, что решения, близкие по начальным значениям к решению 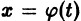
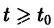
уравнения (1) устойчиво, если, какой бы узкой ни была е-полоска, содержащая кривую 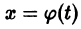
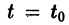
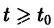
Если при сколь угодно малом 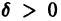
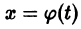
Определение:
Решение 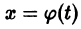
1) решение 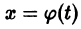
2) существует 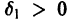
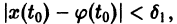
Это означает, что все решения х = x(t), близкие по начальным условиям к асимптотически устойчивому решению 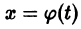
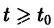
Вот простая физическая модель. Пусть шарик лежит на дне полусферической лунки (находится в положении равновесия). Если малым возмущением вывести шарик из этого положения, то он будет колебаться около него. При отсутствии трения положение равновесия будет устойчивым, при наличии трения колебания шарика будут уменьшаться с возрастанием времени, т. е. положение равновесия будет асимптотически устойчивым.
Пример:
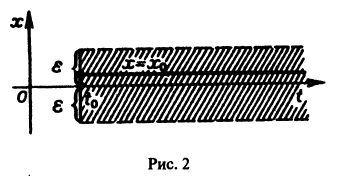
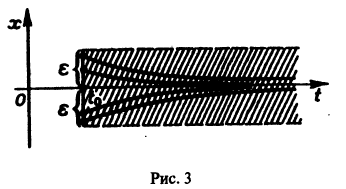
Исследовать на устойчивость тривиальное решение
Решение 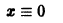
Решение уравнения (*), удовлетворяющее начальному условию
Легко видеть (рис. 2), что, какова бы ни была 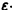
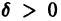
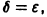
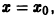
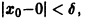
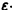
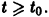
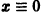
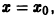
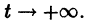
Пример:
Исследовать на устойчивость тривиальное решение 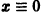
Решение уравнения (**), удовлетворяющее начальному условию
Возьмем любое 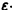
Поскольку 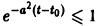
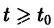
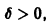
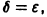
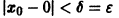
Согласно определению (1) это означает, что решение 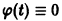
поэтому решение 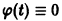
Пример:
Показать, что решение
В самом деле, при сколь угодно малом 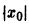
этого уравнения не удовлетворяет условию
при достаточно больших t > to. Более того, при любых 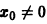
Рассмотрим теперь систему дифференциальных уравнений
где функции fi определены для 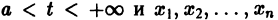
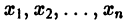
Определение:
системы (4) называется устойчивым по Ляпунову при 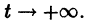
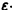
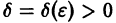
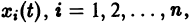
для всех 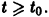
Если при сколь угодно малом 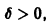
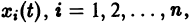
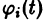
Определение:
системы (4) называется асимптотически устойчивым, если:
1) решение это устойчиво;
2) существует 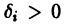
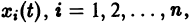
Пример:
Исходя из определения устойчивости по Ляпунову, показать, что решение системы
удовлетворяющее начальным условиям
устойчиво.
Решение системы (*), удовлетворяющее начальным условиям (**), есть
Решение этой системы, удовлетворяющее условиям 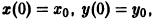
Возьмем произвольное 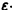
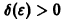
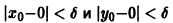
для всех 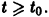
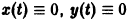
то при 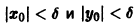
для всех 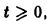
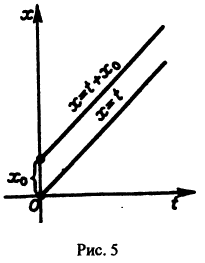
Из устойчивости нетривиального решения дифференциального уравнения не следует ограниченности этого решения. Рассмотрим, например, уравнение
Решением этого уравнения, удовлетворяющим условию х(0) = 0, является функция
Решение, удовлетворяющее начальному условию 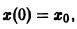
Геометрически очевидно (рис.5), что для всякого 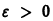
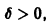
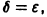
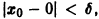
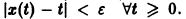
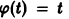
Из ограниченности решений дифференциального уравнения не следует устойчивости решений.
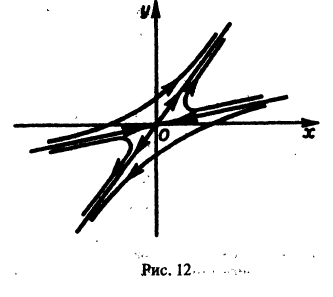
Рассмотрим уравнение
Оно имеет очевидные решения
Интегрируя уравнение (6), находим
Все решения (7) и (8) ограничены на 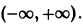
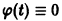
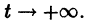
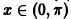
Таким образом, ограниченность и устойчивость решений являются понятиями, независимыми друг от друга.
Замечание:
Исследуемое на устойчивость решение
системы (4) всегда можно преобразовать в тривиальное решение
другой системы заменой
В самом деле, пусть имеем (для простоты) одно дифференциальное уравнение
и пусть требуется исследовать на устойчивость какое-либо решение 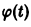
(величину 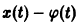
и подстановка в (*) приводит к равенству
Но 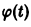
Обозначив здесь правую часть через F(t, у), получим
Это уравнение имеет решение 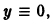
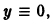
Таким образом, вопрос об устойчивости решения 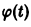
Видео:Дифференциальные уравнения 1. Зависимость решений от параметров и начальных данныхСкачать

Устойчивость автономных систем. Простейшие типы точек покоя
Нормальная система дифференциальных уравнений называется автономной, если ее правые части fi не зависят явно от t, т. е. если она имеет вид
Это значит, что закон изменения неизвестных функций, описываемый автономной системой, не меняется со временем, как это бывает с физическими законами. Пусть имеем автономную систему
и пусть (а1, a2, …, аn) — такая совокупность чисел, что
Тогда система функций
будет решением системы (1). Точку 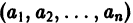
есть точка покоя этой системы. Обозначим через S(R) шар
и будем считать, что для рассматриваемой системы в шаре S(R) выполнены условия теоремы существования и единственности решения задачи Коши.
Определение:
Будем говорить, что точка покоя
системы (1) устойчива, если для любого 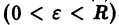
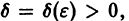
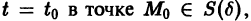
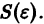
1) она устойчива;
2) существует такое 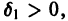
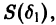
Поясним это определение примерами.
Пример:
Траектории здесь — концентрические окружности
с центром в начале координат — единственной точкой покоя системы. Если взять 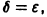
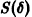
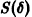
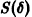
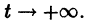
Пример:
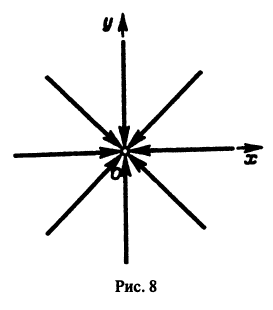
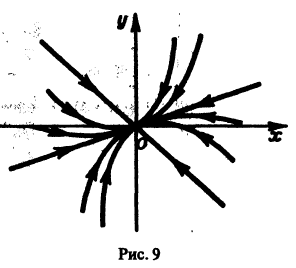
Пусть дана система
поэтому траекториями являются лучи, входящие в начало координат (рис.8). Можно снова выбрать 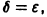
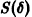
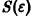
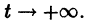
Пример:
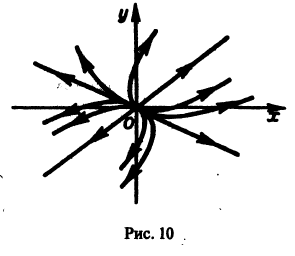
Возьмем, наконец, систему
и траекториями являются лучи, исходящие из начала координат, но в отличие от примера 2 движение по лучам происходит в направлении от центра. Точка покоя неустойчива.
Видео:Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать

Простейшие типы точек покоя
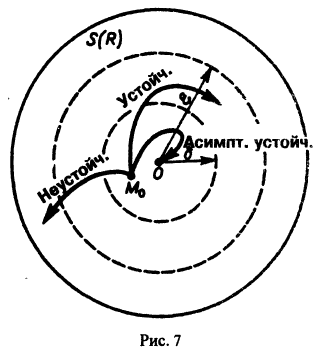
Исследуем расположение траекторий в окрестности точки покоя х = 0, у = 0 системы двух линейных однородных уравнений с постоянными коэффициентами:
Решение будем искать в виде
Для определения 
Величины 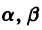
Возможны следующие случаи.
А. Корни 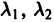
- Пусть
Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей
все точки каждой траектории, находившиеся в начальный момент
в произвольной
окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой,
окрестности начала координат, а при
стремятся к этому началу. Такая точка покоя называется устойчивым узлом
При С2 = 0 из (4) получаем
и траекториями являются два луча, входящие в начало координат с угловым коэффициентом
Аналогично, при С1 = 0 получаем еще два луча, входящие в начало координат с угловым коэффициентом
Пусть теперь 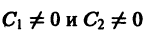
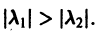
т. е. все траектории (исключая лучи 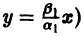
2. Если 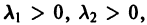
Пример:
Для нее точка О(0,0) — точка покоя. Характеристическое уравнение
имеет корни 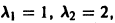
Оно имеет решения
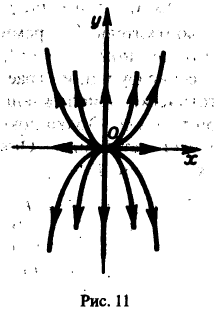
так что траекториями системы будут лучи падающие с координатными полуосями, семейство парабол, касающихся оси Oх в начале координат (рис. 11)
3. Пусть теперь 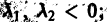
При С2 = 0 получаем решение
С возрастанием t точка этой траектории движется по лучу
в направлении от начала 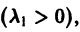
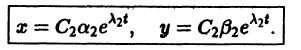
Отсюда видно, что при возрастании t точка движется по лучу
в направлении к началу координат 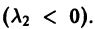
Пример:
Исследуем характер точки покоя О(0,0) системы
Характеристическое уравнение системы
имеет корни 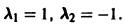
интегрируя которое получаем
Уравнение (6) имеет также решения
Таким образом, интегральные кривые этого уравнения (траектории системы (5)) — равнобочные гиперболы и лучи, совпадающие с координатными полуосями.
Б. Корни 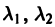
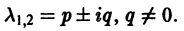
где C1 и C2 — произвольные постоянные, а 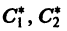
- Пусть
в этом случае множитель
стремится к нулю при
а вторые множители в (7) — ограниченные периодические функции. Траектории — спирали, асимптотически приближающиеся к началу координат при
Точка покоя х = 0, у = 0 асимптотически устойчива. Она называется устойчивым фокусом (рис. 13).,
- Если
то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.
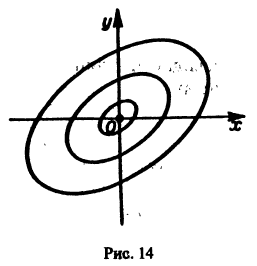
- Если же
то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение
не стремится к нулю при
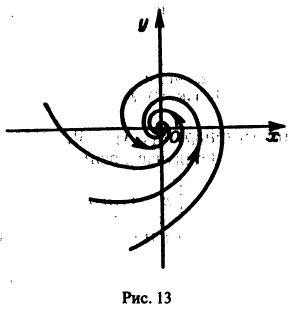
Пример. Рассмотрим систему уравнений
Характеристическое уравнение системы
имеет комплексные корни
Перейдем от системы к одному уравнению
и введем полярные координаты 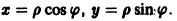
Используя уравнение (9), находим, что
Эти интегральные кривые являются логарифмическими спиралями, навивающимися на начало координат, которое достигается в пределе при 
Интегральные кривые этого уравнения — окружности с центром в начале координат, которое при а = 0 является точкой покоя системы (8) типа центра.
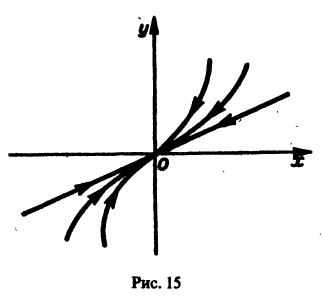
В. Корни 
( 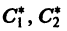
- Если
то из-за наличия множителя
решения х(t), y(t) стремятся к нулю при
Точка покоя х = 0, у = 0 асимптотически устойчива. Ее называют устойчивым вырожденным узлам (рис. 15). Он отличается от узла в случае А. 1 (там одна из траекторий имела касательную, отличную от всех остальных). Возможен также дикритический узел (см. рис. 8).
- При
замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.
Пример:
Для системы уравнений
имеет кратные корни 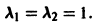
Поэтому все интегральные кривые проходят через начало координат, и все они имеют там ось Оу общей касательной.
Мы перебрали и исчерпали все возможности, поскольку случай 
Пример:
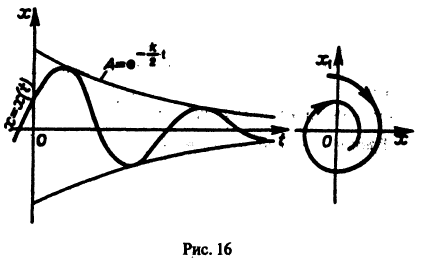
Исследовать уравнение малых колебаний маятника с учетом трения.
Уравнение малых колебаний маятника в этом случае имеет вид
где x — угол малого отклонения маятника от вертикали, к — коэффициент трения. Заменим уравнение (*) эквивалентной системой
Характеристическое уравнение для системы (**)
Если 0
— частота колебаний, а величины А, а определяются из начальных условий.
График решения и фазовая кривая при 0
Сформулируем результаты, касающиеся устойчивости решений системы п линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами
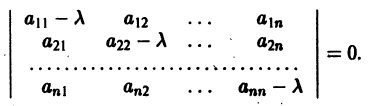
Рассмотрим для системы (10) характеристическое уравнение
Справедливы следующие предложения:
1) если все корни характеристического уравнения имеют отрицательную действительную часть, то все решения системы (10) асимптотически устойчивы. Действительно, в этом случае все слагаемые общего решения содержат множители 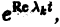
2) если хотя бы один корень 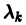
3) если характеристическое уравнение имеет простые корни с нулевой действительной частью (т. е. чисто мнимые или равные нулю корни), а остальные корни, если они есть, имеют отрицательную действительную часть, та все решения устойчивы, но асимптотической устойчивости нет.
Эти результаты относятся и к одному линейному дифференциальному уравнению с постоянными коэффициентами.
Следует обратить внимание на то, что для линейной системы все решения либо устойчивы, либо неустойчивы одновременна
Теорема:
Решения Системы линейных дифференциальных уравнений
либо все одновременно устойчивы, либо неустойчивы.
Преобразуем произвольное частное решение
системы (11) в тривиальное с помощью замены
Система (11) преобразуется при этом в линейную однородную систему относительно yi(t):
Следовательно, все частные решения системы (11) в смысле устойчивости ведут себя одинаково, а именно как тривиальное решение однородной системы (12).
В самом деле, пусть тривиальное решение
системы (12) устойчиво. Это значит, что для любого 
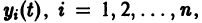
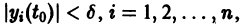
Замечая, что 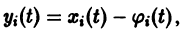
для всякого решения 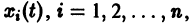
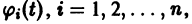
Это предложение не имеет места для нелинейных систем, некоторые решения которых могут быть устойчивыми, а другие — неустойчивыми.
Пример:
Рассмотрим нелинейное уравнение
Оно имеет очевидные решения
Решение x(t) = -1 неустойчиво, а решение x(t) = 1 является асимптотически устойчивым. В самом деле, при 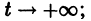
стремятся к +1. Это означает, согласно определению, что решение x(t) = 1 асимптотически устойчиво.
Замечание:
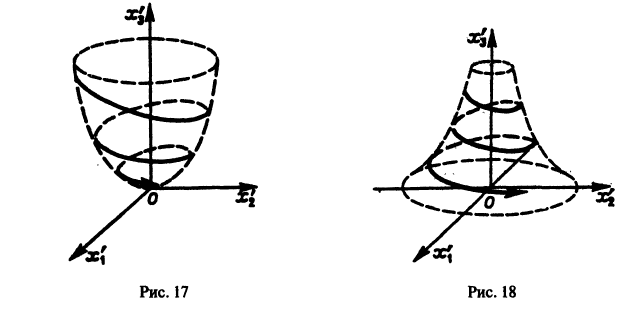
Как и в случае n = 2, можно исследовать расположение траекторий в окрестности точки покоя О(0,0,0) системы (10). Для n = 3 возможны так называемые узлофокусы (рис. 17), седлофокусы (рис. 18) и т. д.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Метод функций Ляпунова
Метод функций Ляпунова состоит в исследовании устойчивости точки покоя системы дифференциальных уравнений с помощью подходящим образом выбранной функции 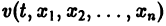
Ограничимся рассмотрением автономных систем
для которых Xi = 0, i = 1, 2,…, n, есть точка покоя.
Идея метода состоит в следующем. Предположим, что на устойчивость исследуется точка покоя 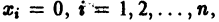
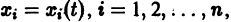
(производная вдоль траектории): Правая часть в (2) есть известная функция от х1, х2,…, хn, и можно исследовать ее знак. Если окажется, что 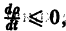
Определение:
Функция v(x1, х2, … xn), определенная в некоторой окрестности начала координат, называется знакоопределенной (знакоположительной или знакоотрицательной), если в области G
где h — достаточно малое положительное число, она может принимать значения только одного определенного знака и обращается в нуль лишь при
Так, в случае n = 3 функции
будут знакоположительными, причем здесь величина h > 0 может быть взята сколь угодно большой.
Определение:
Функция 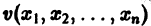
будет знакопостоянной (положительной). В самом деле, функцию v(x1, x2, x3) можно представить так:
отсюда видно, что она неотрицательна всюду, но обращается в нуль и при 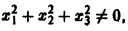
Пусть 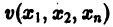
являются некоторыми функциями времени, удовлетворяющими системе дифференциальных уравнений (1). Тогда для полной производной функции v повремени имеем
Определение:
Величина 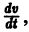
Определение:
Функций 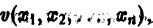
1) 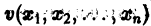
2) 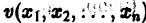
3) полная производная 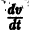
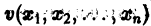
всюду в 
Теорема:
Теорема Ляпунова об устойчивости. Если для системы дифференциальных уравнений
существует дифференцируемая знакоопределенная функция 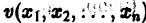
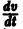
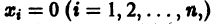
Приведем идею доказательства. Пусть для определенности 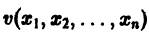
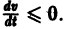
причем v = 0 лишь при 
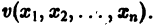
функции v являются, Как можно показать, замкнутыми поверхностями, внутри которых находится начало координат. Чтобы картина стала нагляднее, остановимся на случае n = 2. Так как 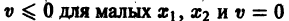
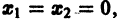
в общих чертах напоминает параболоид, вогнутый Вверх (рис. 19).
Линии уровня 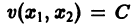
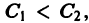
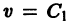
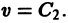
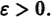
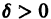
существует дифференцируемая знакоопределенная функция 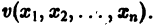
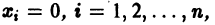
Пример:
Исследовать на устойчивость точку покоя О(0,0) системы
Выберем в качестве функции v(x, y) функцию
Эта функция знакоположительная. В силу системы (*) найдем
Из теоремы 3 следует, что точка покоя О(0,0) системы (*) устойчива (центр). Асимптотической устойчивости нет, так как траектория системы (*) — окружности.
Пример 2. Исследовать на устойчивость точку покоя О(0,0) системы
Таким образом, 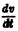
Теорема:
О неустойчивости. Пусть для системы дифференциальных уравнений
существует дифференцируемая в окрестности начала координат функция 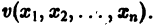
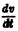
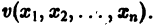
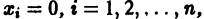
Пример:
Исследовать на устойчивость точку покоя О(0,0) системы
Для нее функция
знакоположительная. Так как сколь угодно близко к началу координат найдутся точки, в которых v > 0 (например, 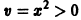
Метод функций Ляпунова оказывается универсальным и эффективным для широкого круга проблем теории устойчивости. Недостаток же метода в том, что достаточно общего конструктивного способа построения функций Ляпунова пока нет. В простейших случаях функцию Ляпунова можно искать в виде
Видео:Дифференциальные уравнения. Теоретический билет 13. Непрерывная зависимость от н.у. и параметраСкачать

Устойчивость по первому (линейному) приближению
Пусть имеем систему дифференциальных уравнений
и пусть 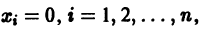
Будем предполагать, что функции 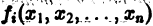
а слагаемые Ri содержат члены не ниже второго порядка малости относительно 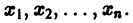
Так как понятие устойчивости точки покоя O(0,0,…, 0) связано с малой окрестностью начала координа’т в- фазовом пространстве, то естественно ожидать, что поведение решения (1) будет определяться главными линейными членами разложения функций fi по х. Поэтому наряду с системой (3) рассмотрим систему
называемую системой уравнений первого (линейного) приближения для системы (3).
Вообще говоря, строгой связи между системами (3) и (4) нет. Рассмотрим, например, уравнение
Здесь f(x) = 0; линеаризированное уравнение для уравнения (5) имеет вид
Решение 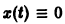
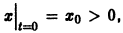
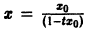
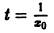
Теорема:
Если все корни характеристического уравнения
имеют отрицательные действительные части, то точка покоя 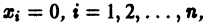
При выполнении условий теоремы возможно исследование на устойчивость по первому приближению.
Теорема:
Если хотя бы один корень характеристического уравнения (7) имеет положительную действительную часть, то точка покоя Xi= 0 системы (4) и системы (3) неустойчива.
В этом случае также возможно исследование на устойчивость по первому приближению.
Наметим идею доказательства теорем 6 и 7.
Пусть для простоты корни 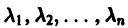
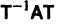
где 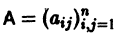
и система (4) преобразуется к виду
или, в силу выбора матрицы Т,
Система (3) при том же преобразовании перейдет в систему
причем в 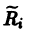
Рассмотрим следующие возможности:
1. Все корни 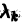
тогда производная 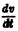
где 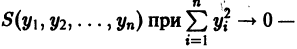
Таким образом, в достаточно малой окрестности 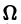
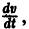
2. Некоторые из корней 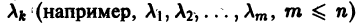
Отсюда видно, что сколь угодно близко к началу координат найдутся точки (например, такие, у которых 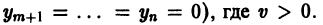
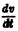
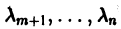
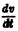
В критическом случае, когда все действительные части корней характеристического уравнения неположительны, причем действительная часть хотя бы одного корня равна нулю, на устойчивость тривиального решения системы (3) начинают влиять нелинейные члены Ri и исследование на устойчивость по первому приближению становится невозможным.
Пример:
Исследовать на устойчивость по первому приближению точку покоя х = 0, у = 0 системы
Система первого приближения имеет вид
Нелинейные члены удовлетворяют нужным условиям: их порядок не меньше 2. Составляем характеристическое уравнение для системы (**):
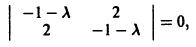
Корни характеристического уравнения 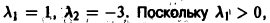
Пример:
Исследуем на устойчивость точку покоя О(0, 0) системы
Точка покоя х = 0, у = 0 системы (*) асимптотически устойчива, так как для этой системы функция Ляпунова
удовлетворяет условиям теоремы Ляпунова об асимптотической устойчивости. В частности,
В то же время точка покоя х = 0, у = 0 системы
В самом деле, для функции 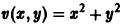
т.е. 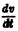
В силу теоремы 5 заключаем о неустойчивости точки покоя О(0,0) системы (**).
Для системы (*) и (**) система первого приближения одна и та же:
для системы (***) имеет чисто мнимые корни — критический случай (действительные части корней характеристического уравнения равны нулю). Для системы первого приближения (***) начало координат является устойчивой точкой покоя — центром. Системы (*) и (**) получаются малым возмущением правых частей (***) в окрестности начала координат. Однако эти малые возмущения приводят к тому, что для системы (*) точка покоя О(0,0) становится асимптотически устойчивой, а для системы (**) неустойчивой.
Этот пример показывает, что в критическом случае нелинейные члены могут влиять на устойчивость точки покоя.
Задача. Исследовать на устойчивость точку покоя О(0,0) системы
где функция f(х,у) разлагается в сходящийся отеленной ряд и f(0,0) = 0.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

23. Нормальные системы линейных однородных дифференциальных
Уравнений с постоянными коэффициентами.
При рассмотрении систем дифференциальных уравнений ограничимся случаем системы трех уравнений (n = 3). Все нижесказанное справедливо для систем произвольного порядка.
Определение. Нормальная система дифференциальных уравнений c постоянными коэффициентами называется Линейной однородной, если ее можно записать в виде:

Решения системы (2) обладают следующими свойствами:
Решения системы ищутся в виде:
Подставляя эти значения в систему (2) и перенеся все члены в одну сторону и сократив на Ekx, получаем:
Для того, чтобы полученная система имела ненулевое решение необходимо и достаточно, чтобы определитель системы был равен нулю, т. е.:
В результате вычисления определителя получаем уравнение третьей степени относительно K. Это уравнение называется Характеристическим уравнением И имеет три корня K1, K2, K3. Каждому из этих корней соответствует ненулевое решение системы (2):
Линейная комбинация этих решений с произвольными коэффициентами будет решением системы (2):
Пример. Найти общее решение системы уравнений:
Составим характеристическое уравнение:
Решим систему уравнений:
Для K1:
Полагая 
Для K2:
Полагая 
Общее решение системы:
Этот пример может быть решен другим способом:
Продифференцируем первое уравнение:
Подставим в это выражение производную У¢ =2X + 2Y из второго уравнения.
Подставим сюда У, выраженное из первого уравнения:
Обозначив 
Пример. Найти решение системы уравнений
Эта система дифференциальных уравнений не относится к рассмотренному выше типу, т. к. не является однородным (в уравнение входит независимая переменная Х).
Для решения продифференцируем первое уравнение по Х. Получаем:
Заменяя значение Z’ из второго уравнения получаем: 
С учетом первого уравнения, получаем:
Решаем полученное дифференциальное уравнение второго порядка.
Общее решение однородного уравнения:
Теперь находим частное решение неоднородного дифференциального уравнения по формуле
Общее решение неоднородного уравнения:
Подставив полученное значение в первое уравнение системы, получаем:
Пример. Найти решение системы уравнений:
Составим характеристическое уравнение:
Если принять g = 1, то решения в этом случае получаем:
Если принять g = 1, то получаем:
Если принять g = 3, то получаем:
Общее решение имеет вид:
Элементы теории устойчивости.
Теория устойчивости решений дифференциальных уравнений является одним из разделов Качественной теории дифференциальных уравнений, которая посвящена не нахождению какого – либо решения уравнения, а изучению характера поведения этого решения при изменении начальных условий или аргумента.
Этот метод особенно важен, т. к. позволяет делать вывод о характере решения без непосредственного нахождения этого решения. Т. е. даже в тех случаях, когда решение дифференциального уравнения вообще не может быть найдено аналитически.
Пусть имеется некоторое явление, описанное системой дифференциальных уравнений:

И начальные условия:
Для конкретного явления начальные условия определяются опытным путем и поэтому неточны.
Теорема. (о непрерывной зависимости решения от начальных условий)
Если правая часть дифференциального уравнения 








Эта теорема справедлива как для одного дифференциального уравнения, так и для системы уравнений.
Определение. Если 


(Ляпунов Александр Михайлович (1857 – 1918) академик Петерб. АН)
Т. е. можно сказать, что решение j(t) устойчиво по Ляпунову, если близкие к нему по начальным условиям решения остаются близкими и при T ³ T0.
Если 
Исследование на устойчивость по Ляпунову произвольного решения 


Система (2) имеет тривиальное (равное нулю) решение
Теорема. Решение 
Это тривиальное решение называется Положением равновесия Или Точкой покоя.
Определение. Точка покоя 


Теорема. (Теорема Ляпунова). Пусть задана система
Имеющая тривиальное решение 
Пусть существует дифференцируемая функция 
1) 
2) Полная производная функции V Вдоль фазовой траектории (т. е. вдоль решения Yi(T) системы (1)) удовлетворяет условию:

Тогда точка покоя 
Если ввести дополнительное требование, чтобы вне сколь угодно малой окрестности начала координат 
Где B — постоянная величина, то точка покоя 
Функция V называется Функцией Ляпунова.
Классификация точек покоя.
Рассмотрим систему двух линейных дифференциальных уравнений с постоянными коэффициентами
Характеристическое уравнение этой системы имеет вид:
Рассмотрим следующие возможные случаи:
1) Корни характеристического уравнения действительные, отрицательные и различные.
Точка покоя 
2) Корни характеристического уравнения действительны и


В этом случае точка покоя также будет устойчива.
3) Хотя бы один из корней 
В этом случае точка покоя 
4) Оба корня характеристического уравнения положительны 
В этом случае точка покоя 
Если полученного решения 

Возможны следующие случаи:

Устойчивый узел. Неустойчивый узел. Седло.
5) Корни характеристического уравнения комплексные 
Если Р = 0, т. е. корни чисто мнимые, то точка покоя (0, 0) устойчива по Ляпунову.
Такая точка покоя называется Центром.
Если P 0, то точка покоя неустойчива и называется Неустойчивым фокусом.
Уравнения математической физики.
Уравнения в частных производных.
Определение. Дифференциальным уравнением в частных производных Называется уравнение относительно неизвестной функции нескольких переменных, ее аргументов и ее частных производных различных порядков.
Порядком Дифференциального уравнения в частных производных называется порядок старшей производной, входящей в это уравнение. Решением Уравнения будет некоторая функция 
Видео:Сергеев И. Н. - Дифференциальные уравнения II - Зависимость решений от параметровСкачать

Обыкновенные дифференциальные уравнения
Содержание:
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Обыкновенные дифференциальные уравнения
При решении многих задач математики, техники, экономики и других отраслей науки бывает трудно установить закон, связывающий искомые и известные переменные величины. Но удается установить связь между производными или дифференциалами этих переменных, которая выражается уравнениями или системами уравнений. Такие уравнения называют дифференциальными уравнениями. Термин «дифференциальное уравнение» введен в 1676 году В. Лейбницом.
Мы рассмотрим только уравнения с функциями одной переменной и обычными производными, которые называют обычными дифференциальными уравнениями.
Основные понятия о дифференциальных уравнениях
Определение. Дифференциальным уравнением называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и еепроизводные или дифференциалы разных порядков, то есть уравнение

Важно понять, что искомая функция в дифференциальном уравнении входит под знак дифференциала или под знак производной.
Определение. Порядком дифференциального уравнения называется наивысший порядок производной от неизвестной функции, входящей в дифференциальное уравнение.
Так, уравнение y’ – 2 xy 2 + 5 = 0 является дифференциальным уравнением первого порядка, а уравнения y» + 2 y’ – y – sin x = 0 — дифференциальным уравнением второго порядка.
Определение. Решением дифференциального уравнения (7.1) называется такая функция y = φ (x), которая при подстановке в уравнение (7.1) превращает его в тождество.
Например, для дифференциального уравнения
y’- 2 x = 0 (7.2)
решением является функция y = x 2 . Найдем производную y’= 2x и подставим в уравнение, получим: 2x – 2x = 0, 0 ≡ 0.
Следует заметить, что y = x 2 не единственное решение уравнения. Это уравнение имеет бесконечное множество решений, которые можно записать так: y = x 2 + C.
Дифференциальные уравнения первого порядка
Определение. Дифференциальным уравнением первого порядка называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и ее первую производную:
F (x, y, y’) = 0. (7.3)
Поскольку производную можно записать в виде отношения дифференциалов, то в уравнение производная может не входить, а будут входить дифференциалы неизвестной функции и независимой переменной.
Если уравнение (7.2) решить относительно у’, то оно будет иметь вид:
y’= f (x, y) или 
Простые примеры показывают, что дифференциальное уравнение может иметь бесконечное множество решений. Это мы видим на примере уравнения (7.2). Легко убедиться также, что дифференциальное уравнение 


Как видим, в решение указанных дифференциальных уравнений входит произвольное число C. Предоставляя постоянной C различные значения, будем получать различные решения дифференциального уравнения.
Определение. Общим решением дифференциального уравнения (7.3) называется функция
у = φ (х, С), (7.5)
которая зависит от одной произвольной постоянной и удовлетворяет дифференциальное уравнение при произвольном значении C.
Если функция (7.5) выражается неявно, то есть в виде
Ф (х, у, С) = 0, (7.6)
то (7.6) называется общим интегралом дифференциального уравнения.
Определение. Частным решением дифференциального уравнения (7.3) называется такое решение, которое получается из общего решения (7.5) при некотором конкретном значении постоянной C.
Ф (х, у, С0) называется частным интегралом дифференциального уравнения.
На практике при решении конкретных задач часто приходится находить не все решения, а решение, которое удовлетворяет определенным начальным условиям. Одной из таких задач является задача Коши, которая для дифференциального уравнения первого порядка формулируется так: среди всех решений дифференциального уравнения (7.3) найти такое решение y, которое при заданном значении независимой переменной x = x0 равна заданному значению y0 , то есть y (x0) = y0 или 
Условие (7.7) называется начальным условием решения.
Покажем на примере, как найти частное решение дифференциального уравнения, когда известно общее решение и задано начальное условие.
Мы видим, что дифференциальное уравнение 

Ответ на вопрос о том, при каких условиях уравнение (7.4) имеет
решение, дает теорема Коши.
ТЕОРЕМА (о существовании и единственности решения). Если функция f (x, y) и ее частная производная 
Теорема Коши дает достаточные условия существования единого решения дифференциального уравнения (7.4). Заметим, что в условии теоремы не требуется существования частной производной 
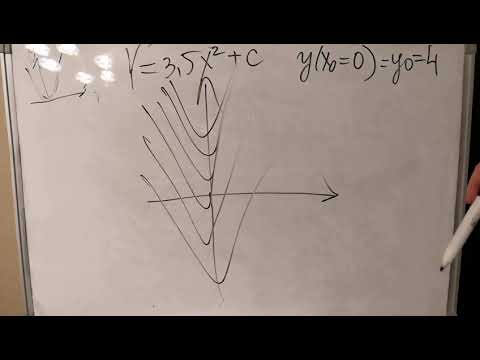
График произвольного частного решения дифференциального уравнения называется интегральной кривой. Общему решению отвечает семья кривых. Так мы проверили, что уравнение 
которые проходят через начало координат (рис. 1).
Уравнение 
Если задано начальное условие 
интегральных кривых мы выбираем проходящую через точку M0 (x0; y0).
Надо заметить, что нахождение решения дифференциального уравнения часто называют интегрированием уравнения. При этом операцию интегрирования функций называют квадратурой.
Общего метода решения дифференциальных уравнений первого порядка не существует. Рассмотрим некоторые методы решения отдельных типов дифференциальных уравнений.
Дифференциальные уравнения с разделенными переменными
Определение. Уравнение вида
f1 (y) dy = f2 (x) dx, (7.8)
где f1 (y) и f2 (x) — заданные функции, называется дифференциальным уравнением с разделенными переменными.
В этом уравнении каждая из переменных находится только в той части уравнения, где находится ее дифференциал. Уравнение dy = f (x) dx является частным случаем уравнения (7.8). Чтобы решить уравнение (7.8), надо проинтегрировать обе его части: 
Понятно, что произвольную постоянную С можно записывать в любой части равенства.
Пример 1. Решить дифференциальное уравнение: 
Решение. Проинтегрируем левую и правую части уравнения, причем для удобства потенцирования, произвольную постоянную запишем в виде ln |C| получим: 


Подставляя в общее решение начальное условие, найдем С: 2 = С.
Итак,

Дифференциальные уравнения с разделяющимися переменными
Определение. Уравнение вида
f1 (x) f2 (y) + g1 (x) g2 (y) = 0 (7.9)
называется дифференциальным уравнением с разделяющимися переменными.
В этом уравнении переменные еще не разделены, но, поделив обе части уравнения на произведение f2 (y) g1 (x), получим уравнение с разделенными переменными:
Интегрируя это уравнение, запишем 
Получили общий интеграл данного уравнения.
Пример 2. Решить дифференциальное уравнение
x (y + 1) dx – (x 2 + 1) ydy = 0.
Решение. Поделим обе части этого уравнения на (y + 1) (x 2 + 1), после чего получим 
Интегрируя, получим



Пример 3. Найти частное решение дифференциального уравнения (1 + x 2 ) dy + ydx = 0, удовлетворяющее начальному условию y (0) = 1.
Решение. Отделим переменные, поделив уравнение на y ⋅ (1 + x 2 ), и проинтегрируем данное уравнение:
Получили общий интеграл дифференциального уравнения.
Используя начальное условие, найдем произвольную постоянную С:
ln 1 + arctg 0 = C, откуда C = 0.
Найденную постоянную подставим в общий интеграл и отыщем частное решение:

Однородные дифференциальные уравнения
Определение. Функция двух переменных f (x, y) называется однородной n- го измерения, если выполняется условие
Например, f (x, y) = x 2 + y 2 , f (tx, ty) = t 2 f (x 2 + y 2 ) — однородная функция второго измерения.
Определение. Дифференциальное уравнение
y ‘= f (x, y) (7.10)
называется однородным, если функция f (x, y) однородная нулевого измерения.
Покажем, что это уравнение можно свести к уравнению с разделенными переменными.
Рассмотрим функцию f (tx, ty). Сделаем замену 

Тогда уравнение (7.10) запишется в виде 
В общем случае переменные в однородном уравнение не разделяются сразу. Но, если ввести вспомогательную неизвестную функцию u = u (x) по формуле

то мы сможем превратить однородное уравнение в уравнение с разделенными переменными.
Из формулы (7.12) найдем y’ = u + xu’ и уравнение 
то есть 

После интегрирования получим 
Отсюда находим выражение для функции u, возвращаемся к переменной y = xu и получим решение однородного уравнения.
Чаще всего не удается найти функцию u явно выраженной, тогда, после интегрирования, в левую часть следует подставить 
В результате получим решение уравнения в неявном виде.
Пример 1. Найти решение однородного уравнения
Решение. Заменой y = xu сведем заданное уравнение к уравнению


Отделяя переменные, найдем




Возвращаясь к переменной y, получим общее решение: 
Линейные дифференциальные уравнения
Определение. Линейным дифференциальным уравнением первого порядка называется уравнение, которое содержит искомую функцию и ее производную в первой степени без их произведения:
y’ + P (x) y = Q (x). (7.13)
Здесь P (x), Q (x) — известные функции независимой переменной x. Например, y’ + 2 xy = x 2 .
Если Q (x) = 0, то уравнение (7.13) называется линейным однородным и является уравнением с разделяющимися переменными.
Если Q (x) ≠ 0, то уравнение (7.13) называется линейным неоднородным, которое можно решить несколькими способами.
Рассмотрим метод Бернулли, с помощью которого уравнение (7.13) можно свести к интегрированию двух дифференциальных уравнений первого порядка с разделяющимися переменными.
Решение дифференциального уравнения (7.13) ищем в виде y = u (x) v (x) или y = uv, (7.14)
где u (x), v (x) — неизвестные функции. Одну из этих функций можно взять произвольную, а другая определяется из уравнения (7.13).
Из равенства y = uv найдем производную y’:
y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение (7.13):
u’v + uv’ + P (x) ⋅ u⋅ v = Q (x) или u’v + u (v’ + P (x) ⋅ v) = Q (x).
Выберем функцию v такой, чтобы v’ + P (x) v = 0. (7.15)
Тогда для отыскания функции u получим уравнение:
u’v = Q (x). (7.16)
Сначала найдем v из уравнения (7.15).
Отделяя переменные, имеем 
Под неопределенным интегралом здесь будем понимать какую-то одну первообразную от функции P (x), то есть v будет определенной функцией от x.
Зная v, находим u из уравнения (7.16): 
откуда
Здесь мы уже берем для u все первообразные.
Найденные функции u и v подставляем в (7.14) и получаем общее решение линейного дифференциального уравнения:

При решении конкретных примеров проще выполнять эти выкладки, чем применять громоздкую формулу (7.17).
Пример 1. Решить дифференциальное уравнение 
Решение. Решение ищем в виде y = uv, тогда y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение: 

Выражение, стоящее в скобках, приравниваем к нулю, имеем

Отделим переменные, домножив обе части уравнения на 

После интегрирования, получим ln |v| = ln |x| (здесь ограничимся одной первообразной), откуда v = x.
Подставим v = x в уравнение (7.18):
Общее решение запишется:
y = x (x + C) = x 2 + Cx.
Пример 2. Найти частное решение дифференциального уравнения 
Решение. Заданное уравнение — это линейное неоднородное уравнение первого порядка, решение которого ищем в виде y = u⋅v.
Тогда 
Подставим v в уравнение и найдем u:
Общее решение дифференциального уравнения будет:
Подставляем начальные условия в найденное решение и находим С:
Из общего решения получаем частное решение 
Дифференциальное уравнение Бернулли
Определение. Уравнения вида


называется дифференциальным уравнением Бернулли.
Данное уравнение отличается от уравнения (7.13) только множителем y» (или x») в правой части. Для того, чтобы права часть данного уравнения была такой, как в (7.13), разделим его левую и праву часть на y»:
Сделаем замену: 
Домножим левую и правую части полученного уравнения на (n + 1) и, используя замену, получим: 
Мы получили линейное дифференциальное уравнение относительно новой переменной
Пример 1. Найти общее решение дифференциального уравнения xy’ + y = y 2 ln x.
Решение. 
Сделаем замену 
Данное уравнение решим, сделав замену z = u (x) ⋅ v (x).
Выбираем функцию v (x) так, чтобы выражение в скобках равнялось нулю, и эта функция была бы частным решением уравнения
Тогда 
Проинтегрировав правую часть этого уравнения по частям, получим 
Видео:Общее и частное решение дифференциального уравненияСкачать
Обыновенное дефференциальное уравнение
Обыкновенным дифференциальным уравнением называется любое соотношение, связывающее независимую переменную 


Обыкновенное дифференциальное уравнение может быть приведено к виду
Здесь 
Число 
Обыкновенные дифференциальные уравнения первого порядка, разрешенные относительно производной. уравнения, интегрируемые в квадратурах
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Основные понятия и определения
Понятие об уравнении первого порядка, разрешенном относительно производной. В соответствии со сказанным во введении, уравнение первого порядка имеет вид
В этой главе мы будем рассматривать уравнение, разрешенное относительно производной:
Наряду с этим уравнением мы всегда будем рассматривать перевернутое уравнение
используя последнее в окрестности тех точек, в которых 
Во многих случаях оказывается целесообразным «место уравнении (2) и (2′) рассматривать одно равносильное им дифференциальное уравнение
Обе переменные 

Умножая обе части уравнения (3) на некоторую функцию 
где 


Иногда уравнение записывают *з так называемой симметрической форме:
Возможно вам будут полезны данные страницы:
Решение уравнения. Предположим, что правая часть уравнения (2), 




- Существует производная
для всех значений
из интервала
(Отсюда следует, что решение
представляет собою функцию, непрерывную ею всей области определения).
- Функция
обращает уравнение (2) в тождество:
справедливое для всех значений 





Так как наряду с уравнением (2) рассматривается перевернутое уравнение (2′), то и решения 
В этом смысле в дальнейшем мы будем для краткости называть решения уравнения (2′) решениями уравнения (2).
Примеры с решением
Пример 1.
является решением уравнения
в интервале 
справедливое при всех значениях
Пример 2.
Функция 

Пример 3.
является решением уравнения
в интервале
Иногда функцию 
Видео:Решение физических задач с помощью дифференциальных уравненийСкачать

Системы обыкновенных дифференциальных уравнений
При решении многих задач нужно найти функции y1 = y1 (x), y2 = y2 (x), . yn = yn (x), которые удовлетворяют системе дифференциальных уравнений, содержащих независимую переменную x , искомые y1 , y2 , . yn и их производные.
Пример. Пусть материальная точка массы m имеет криволинейную траекторию движения в пространстве. Определить положение точки в любой момент времени t, когда на нее действует сила 
Положение точки в любой момент времени t определяется ее координатами x, y, z; следовательно, x, y, z являются функциями от t. Проекциями вектора скорости точки на оси координат будут производные x’ , y’ , z’.
Положим, что сила

функции определяются из уравнений динамики:
Мы получили систему трех дифференциальных уравнений второго порядка. В случае движения, когда траектория является плоской кривой, лежит, например, в плоскости Оxy, получим систему двух уравнений для определения неизвестных функций x (t) и y (t):
Рассмотрим простейшие системы дифференциальных уравнений.
Системы дифференциальных уравнений первого порядка
Система n уравнений первого порядка с n неизвестными функциями имеет вид:

где x — независимая переменная, y1, y2, . yn — неизвестные функции.
Если в левой части уравнений системы стоят производные первого порядка, а правые части уравнений вовсе не содержат производных, то такая система уравнений называется нормальной.
Решением системы называется совокупность функций y1, y2, . yn, которые превращают каждое уравнение системы в тождество относительно x.
Задача Коши для системы (7.38) состоит в нахождении функций y1, y2, . yn , удовлетворяющих систему (7.38) и заданные начальные условия:

Интегрирование системы (7.38) делают следующим образом. Дифференцируем по x первое уравнение системы (7.38): 
Заменим производные


Дифференцируем полученное уравнение и, подставив в это равенство значения производных из системы (7.38), найдем 
Продолжая дальше таким образом, получим 
В результате получаем следующую систему уравнений:

Из первых (n-1) уравнений определим y2, y3, . yn:

и подставим их значения в последнее уравнение системы (7.40) для определения y1:
Продифференцируем это выражение (n-1) раз, определим


Для того, чтобы полученное решение удовлетворяло заданным начальным условиям, остается только найти значение произвольных постоянных из уравнений (7.42) и (7.43) так, как мы это делали для одного дифференциального уравнения.
Пример 1. Проинтегрировать систему 
когда заданы начальные условия 
Решение. Дифференцируем по x первое уравнение, имеем: 



Из первого уравнения системы найдем 

Общим решением этого уравнения является

и тогда 
Подберем постоянные С1 и С2 так, чтобы выполнялись начальные условия. На основании (*) и (**) имеем:
1 = С1 – 9; 0 = С2 – 2С1 + 14, откуда С1 = 10, С2 = 6.
Таким образом, решением системы, которое удовлетворяет заданным начальным условиям, будет:
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Система дифференциальных уравнений:

где коэффициенты aij — постоянные числа, t — независимая переменная, x1 (t), . xn (t) —
неизвестные функции, называется системой линейных дифференциальных уравнений с постоянными коэффициентами.
Эту систему можно решать путем сведения к одному уравнению n-го порядка, как это было показано выше. Но эту систему можно решить и другим способом. Покажем, как это делается.
Будем искать решение системы (7.44) в виде:

Надо определить постоянные α1, α2, . αn и k так, чтобы функции (7.45) удовлетворяли систему (7.44). Подставим функции (7.45) в систему (7.44):
Сократим на e kt и преобразуем систему, сведя ее к такой системе:

Это система линейных алгебраических уравнений относительно α1, α2, . αn. Составим определитель системы:
Мы получим нетривиальные (ненулевые) решения (7.45) только при таких k, при которых определитель превратится в ноль. Получаем уравнение n-го порядка для определения k:
Это уравнение называется характеристическим уравнением для системы (7.44).
Рассмотрим отдельные случаи на примерах:
1) Корни характеристического уравнения действительны и различны. Решение системы записывается в виде:
Пример 2. Найти общее решение системы уравнений:
Решение. Составим характеристическое уравнение:

Решение системы ищем в виде
Составим систему (7.46) для корня k1 и найдем 


Откуда 


Итак, мы получили решение системы:
Далее составляем систему (7.46) для k = 4:
Откуда 
Получим второй решение системы: 
Общее решение системы будет:
2) Корни характеристического уравнения различны, но среди них есть комплексные:
k1 = α + iβ, k2 = α – iβ. Этим корням будут отвечать решения:


Можно доказать также, что истинные и мнимые части комплексного решения также будут решениями. Таким образом, получим два частных решения:

где 

Соответствующие комбинации функций (7.49) войдут в общий решение системы.
Пример 3. Найти общее решение системы
Решение. Составляем характеристическое уравнение:

Подставляем поочередно k1, k2 в систему (7.46), найдем
Запишем уравнение (7.47) и (7.48) для наших данных
Перепишем эти решения в таком виде:
За частные решения можно взять отдельно действительные и отдельно мнимые части:
Общим решением системы будет
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
📹 Видео
ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Дифференциальные уравнения. Теоретический билет 10. Непрерывная зависимость решений от параметраСкачать

3. Условия существования и единственности решения задачи КошиСкачать

Пример 65. Решить задачу Коши (диффуры)Скачать

Частное решение дифференциального уравнения. 11 класс.Скачать

Дифференциальные уравнения 13. Зависимость решения задачи Коши от параметра.Скачать

1. Что такое дифференциальное уравнение?Скачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

ДУ Уравнения, не разрешенные относительно производнойСкачать


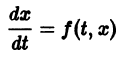
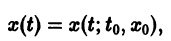
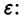
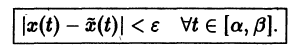
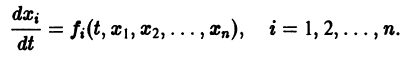
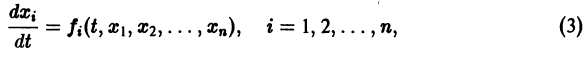
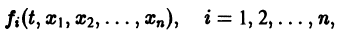
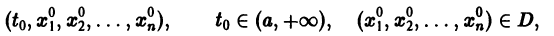
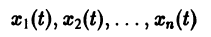
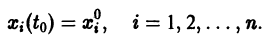
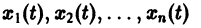
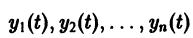
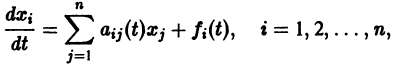
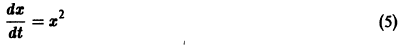
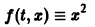
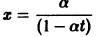
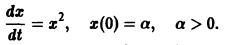
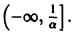
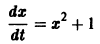


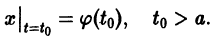
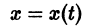
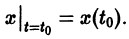


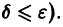

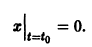
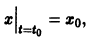
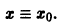
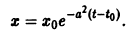
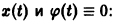
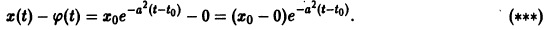
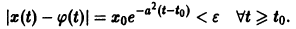
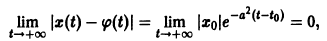
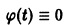
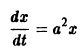
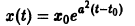
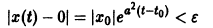
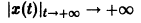
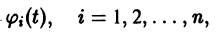
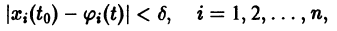
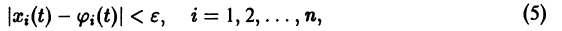
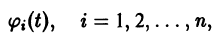
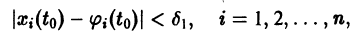
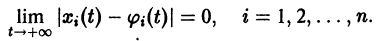


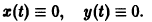
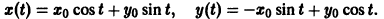
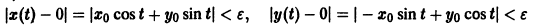
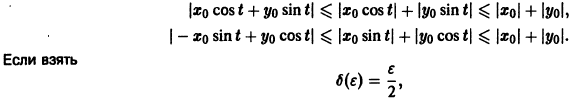
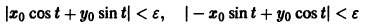
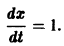
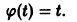
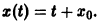


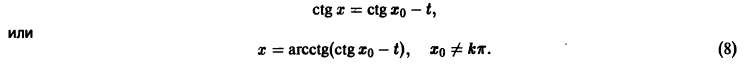
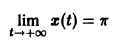
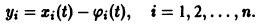

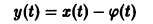
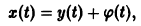

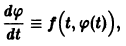
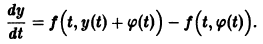

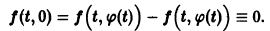
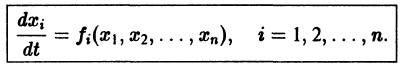
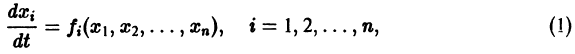
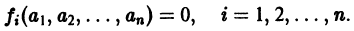
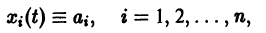
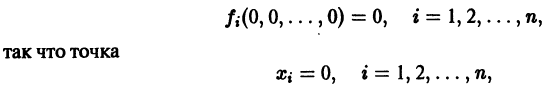
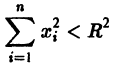
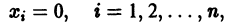
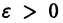
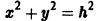
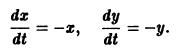
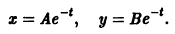
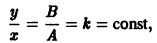
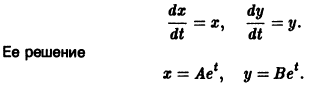
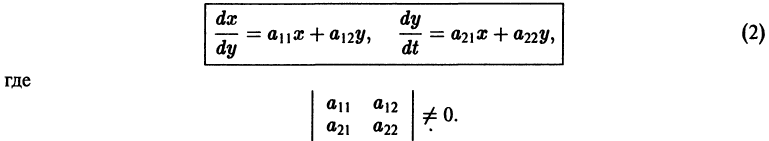
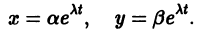
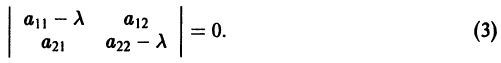
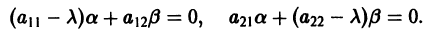
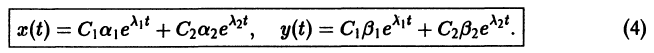
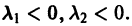 Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей
Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей 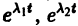 все точки каждой траектории, находившиеся в начальный момент
все точки каждой траектории, находившиеся в начальный момент 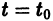 в произвольной
в произвольной  окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой,
окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой, 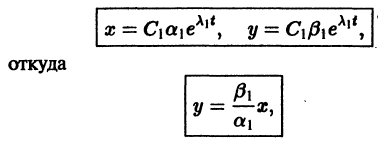
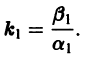
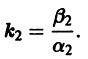
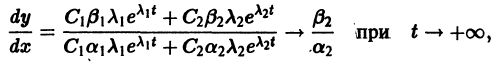
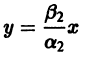
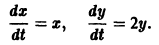
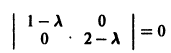
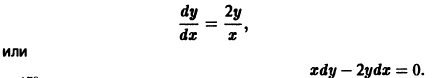

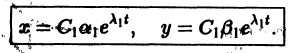
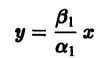
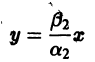
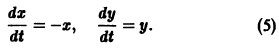
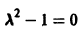
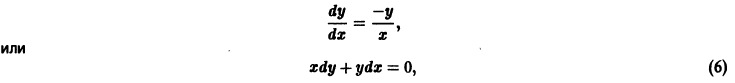
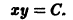
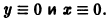
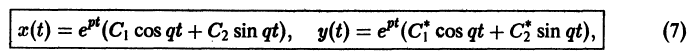
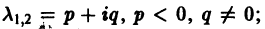 в этом случае множитель
в этом случае множитель 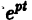 стремится к нулю при
стремится к нулю при 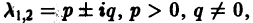 то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.
то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.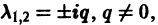 то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение
то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение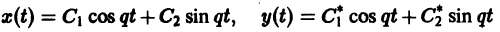
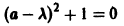
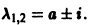

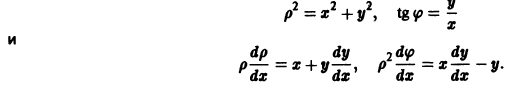
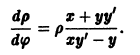

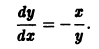
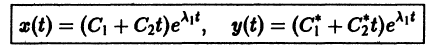
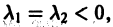 то из-за наличия множителя
то из-за наличия множителя 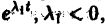 решения х(t), y(t) стремятся к нулю при
решения х(t), y(t) стремятся к нулю при 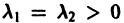 замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.
замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.
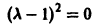
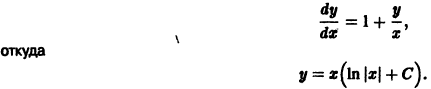
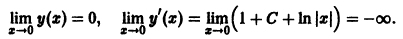
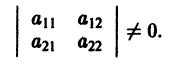



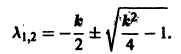
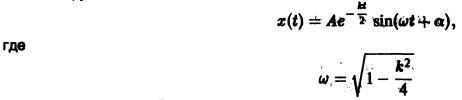
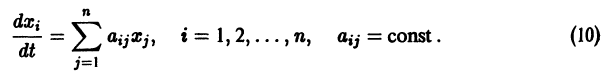
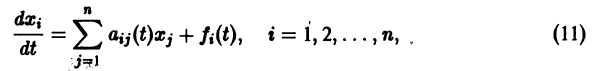
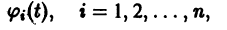
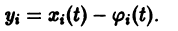
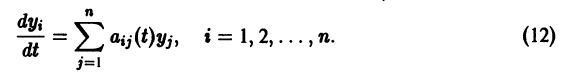
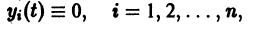
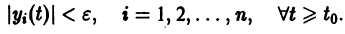
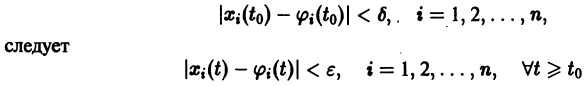
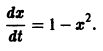
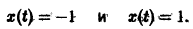
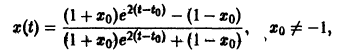
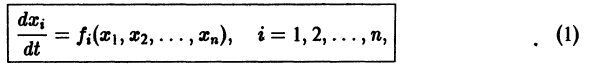
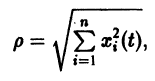
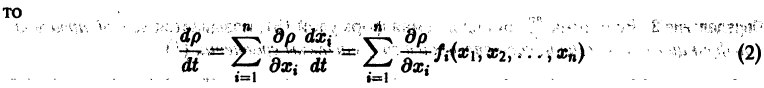
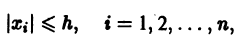



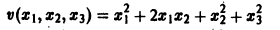
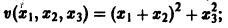
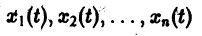
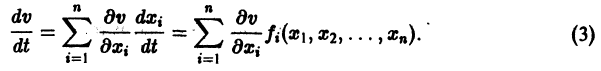
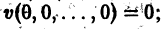
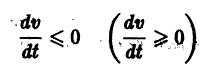
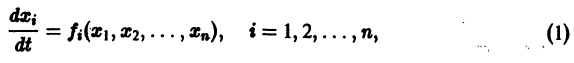
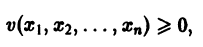
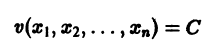
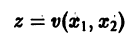
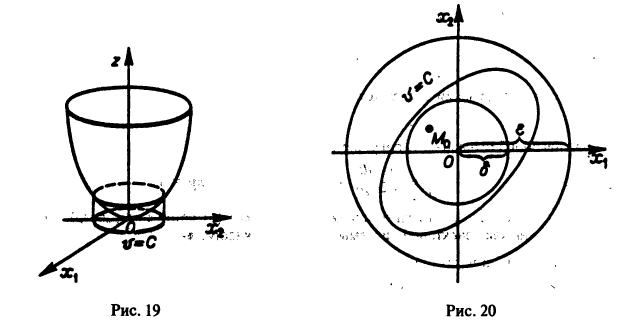
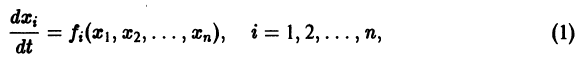

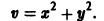
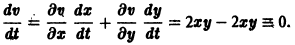
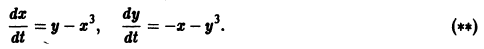
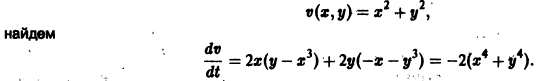
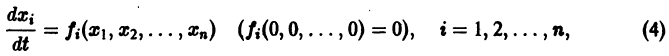
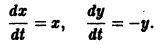
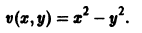
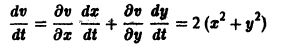
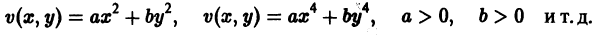
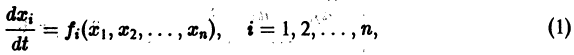
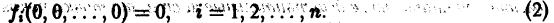
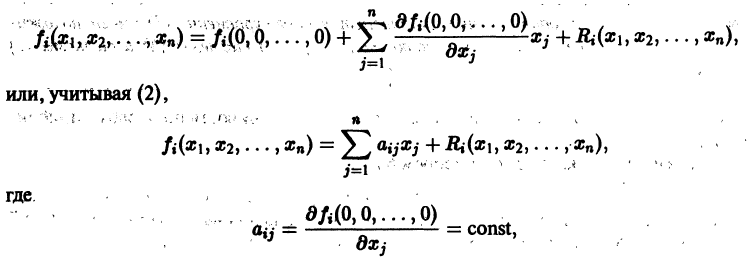
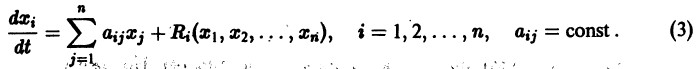
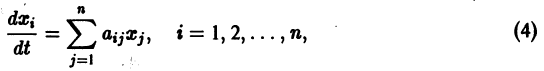

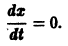
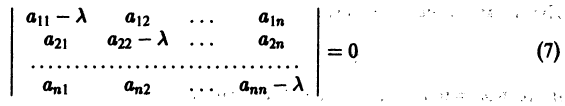
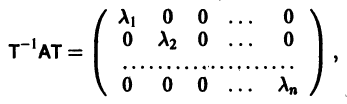
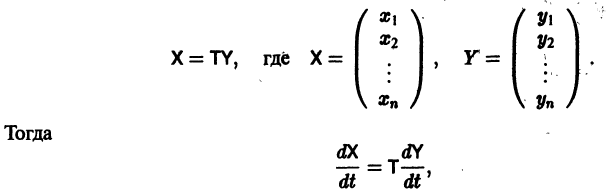
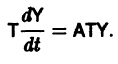
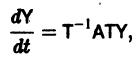
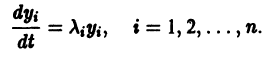
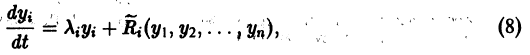
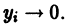
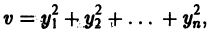
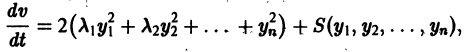
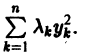
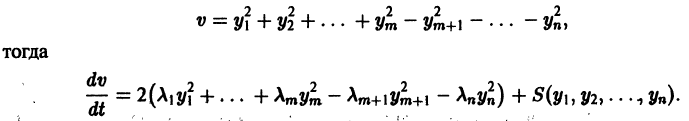
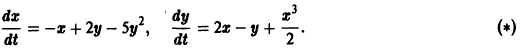
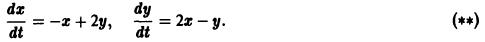

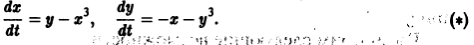
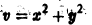
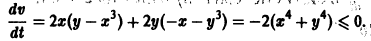

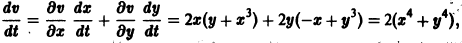
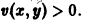

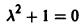
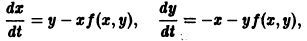






























































































 для всех значений
для всех значений  из интервала
из интервала  (Отсюда следует, что решение
(Отсюда следует, что решение  представляет собою функцию, непрерывную ею всей области определения).
представляет собою функцию, непрерывную ею всей области определения). обращает уравнение (2) в тождество:
обращает уравнение (2) в тождество: 


































