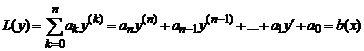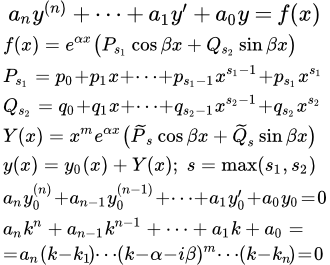Дифференциальные уравнения высших порядков со специальной правой частью

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Уравнения с правой частью специального вида

Общее решение y_ОН линейного неоднородного дифференциального уравнения L(y)=b(x) есть сумма общего решения y_ОО соответствующего однородного уравнения L(y) = 0 и какого — либо частного решения y_ЧН исходного неоднородного уравнения. Для уравнений с постоянными коэффициентами и правой частью специального вида это частное решение может быть найдено достаточно просто.

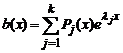
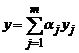
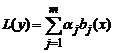
Функцию , где P_j(x) — некоторые полиномы (многочлены), назовём квазиполиномом. По теореме о наложении решений, если y_j , j=1,2. m — решения уравнений L(y) = b_j(x), то есть решение уравнения . Поэтому, не умаляя общности, будем считать, что правая часть уравнения L(y) = b(x) с постоянными коэффициентами имеет вид b(x) = P(x)e λx . В частности, если λ=α+βi — комплексное число, то наиболее общей правой частью указанного типа является функция

(1)

у которой P(x)и Q(x)- некоторые полиномы. Справедлив следующий результат.

Теорема. Линейное дифференциальное уравнение

с постоянными коэффициентами и правой частью вида (1) имеет частное решение

,

где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x) , S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x) , Q(x).

Видео:Дифференциальные уравнения высших порядков, допускающие понижение порядкаСкачать

Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Определение общего решения по известному частному решению

Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами n-го порядка:
(1) ,
где – действительные числа; – действительная функция. Если известно частное (любое) решение уравнения (1), то можно найти его общее решение по формуле:
,
где – общее решение однородного уравнения:
.

Если неоднородная часть может быть представлена в виде суммы функций:
,
то частное решение также может быть представлено в виде суммы частных решений:
,
каждое из которых удовлетворяет уравнению с правой частью в виде одной из функций :
.

Как правило, легче найти частные решения от более простых неоднородных частей, а затем получить частное решение для всего уравнения суммированием полученных частных решений.

Видео:14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Метод решения линейных ДУ с постоянными коэффициентами со специальной неоднородной частью

Рассмотрим линейное неоднородное уравнение со специальной неоднородной частью в виде комбинации многочленов, экспоненты, синусов и косинусов:
(2) ,
где – многочлены степеней и , соответственно:
;
;
– известные коэффициенты.

Это уравнение можно решить общим методом понижения порядка. Однако существует более простой способ, основанный на том, что частное решение такого уравнения имеет определенный вид. Суть этого метода заключается в следующем.

Вначале ищем общее решение однородного уравнения:
(3) .

Далее устанавливаем вид частного решения исходного уравнения (2). Оно выражается через многочлены, экспоненту, синусы и косинусы, которые входят в частное решение с неизвестными коэффициентами. Установив вид частного решения, подставляем в уравнение (2). Приравнивая левую и правую части, находим неизвестные коэффициенты.

После этого общее решение исходного уравнения (2) равно сумме общего решения однородного уравнения плюс частное решение неоднородного:
.

Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Установление вида частного решения

Установим вид частного решения уравнения (2). Для этого вначале ищем решение однородного уравнения (3) в виде . В результате, для k , получаем уравнение, которое называется характеристическим уравнением:
(4) .
Решаем это уравнение. Получаем n корней . Тогда характеристическое уравнение (4) можно представить в виде произведения множителей:
(5) .

Часть корней (или все) в (5) могут быть комплексными. Поэтому выразим корень через действительную и мнимую части:
.
Для действительного корня .

Некоторые корни в (5) могут быть кратными:
.
Здесь p – кратность корня. Кратный корень кратности p входит в произведение (5) в виде множителя .

Если среди корней характеристического уравнения (4) нет корня со значением
,
то частное решение уравнения (2) имеет вид:
,
где – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами , которые подлежат определению подстановкой в уравнение (2).

Если среди корней характеристического уравнения (4) есть корень кратности p со значением

то частное решение уравнения (2) имеет вид:
,
где также – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами .

Когда вид частного решения установлен, подставляем Y в уравнение (2) и находим неизвестные коэффициенты , приравнивая левую и правую части уравнения. После чего получаем общее решение уравнения (2):
.

Видео:ЛНДУ II п. со спец. правой ч. (sin, cos)Скачать

Частные случаи

Неоднородность в виде многочлена

Теперь рассмотрим некоторые более простые виды специальной неоднородности. Начнем с неоднородной части в виде многочлена:
,
где – многочлен степени s . Этот случай принадлежит к общему виду специальной неоднородности (2), в котором . Основываясь на вышеизложенном, получаем следующие правила составления вида частного решения.

Если среди корней характеристического уравнения (4) нет нулевого корня
,
то частное решение имеет вид:
.
То есть оно является многочленом степени s с неопределенными коэффициентами .

Если характеристическое уравнение (4) имеет нулевой корень кратности p :
,
то частное решение имеет вид:
.

Неоднородность в виде произведения экспоненты и многочлена

Теперь рассмотрим неоднородную часть в виде произведения многочлена степени s и экспоненты:
.
Этот случай принадлежит к общему виду (2), в котором .

Если среди корней характеристического уравнения нет действительного корня со значением α :
,
то частное решение является произведением многочлена степени s и экспоненты:
.

Если характеристическое уравнение (4) имеет действительный корень α кратности p :
,
то частное решение имеет вид:
.

Неоднородность в виде суммы произведений многочленов на косинус и синус

Наконец рассмотрим неоднородную часть в виде суммы произведений многочленов степеней на косинус и синус:
.
Этот случай принадлежит к общему виду (2), в котором .

Если среди корней характеристического уравнения нет чисто мнимого корня со значением iβ :
,
то частное решение является суммой произведений многочленов, косинуса и синуса:
,
где – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами .

Если характеристическое уравнение (4) имеет чисто мнимый корень iβ кратности p :
,
то частное решение имеет вид:
.
То есть частное решение как и в предыдущем случае, но умноженное на .

Автор: Олег Одинцов . Опубликовано: 30-07-2013 Изменено: 14-09-2020

Видео:Дифференциальные уравнения, 9 урок, Линейные дифференциальные уравнения высших порядковСкачать

Дифференциальные уравнения высших порядков: ЛОДУ, примеры решения.

Можно выделить 5 возможных метода для определения y₀ — общего решения линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами:

1. В случае, когда все решения характеристического уравнения являются действительными и различными, значит, линейно независимые частные решения принимают вид:

,

а общее решение линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами записывают так:

.

Найти общее решение ЛОДУ 3-го порядка с постоянными коэффициентами:

.

Для начала записываем характеристическое уравнение и находим его корни, перед этим произведя разложение многочлена в левой части равенства на множители методом группировки:

Каждый из трех корней характеристического уравнения являются действительными и различными, значит, общее решение линейного однородного дифференциального уравнения 3-го порядка с постоянными коэффициентами принимает вид:

.

2. Когда каждое решение характеристического уравнения оказывается действительными и одинаковыми, т.е.,

,

значит, линейно независимые частные решения ЛОДУ n-ого порядка с постоянными коэффициентами принимают вид:

,

а общее решение линейного однородного дифференциального уравнения (ДУ) принимает вид:

Найти общее решение ДУ

.

Характеристическое уравнение этого линейного однородного дифференциального уравнения 4-го порядка выглядит так:

.

Обратившись к формуле бинома Ньютона, переписываем характеристическое уравнение как , из чего видим четырехкратный корень k₀ = 2.

Т.о., общим решением заданного ЛОДУ с постоянными коэффициентами является:

.

3. Когда решениями характеристического уравнения ЛОДУ n-ого порядка с постоянными коэффициентами оказываются разные комплексно сопряженные пары , n=2m, тогда линейно независимые частные решения такого линейного однородного дифференциального уравнения принимает вид:

а общее решение записывается так:

Проинтегрировать ЛОДУ 4-го порядка с постоянными коэффициентами .

Характеристическое уравнение этого линейного однородного дифференциального уравнения:

.

Произведя некоторые несложные преобразования и группирования имеем:

Откуда находим 2 пары комплексно сопряженных корней характеристического уравнения и . Тогда, общим решением заданного ЛОДУ n-ого порядка с постоянными коэффициентами является:

4. Когда решениями характеристического уравнения оказываются совпадающие комплексно сопряженные пары , тогда линейно независимые частные решения ЛОДУ n-ого порядка с постоянными коэффициентами выглядят так:

,

а общим решением этого линейного однородного дифференциального уравнения является:

Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами:

.

Первым шагом записываем характеристическое уравнение этого ЛОДУ с постоянными коэффициентами и определяем его корни:

Т.е., решением характеристического уравнения является двукратная комплексно сопряженная пара . Тогда общее решение заданного ЛОДУ с постоянными коэффициентами будет:

.

5. Могут возникнуть любые комбинации случаев, описанных выше, т.е., некоторые корни характеристического уравнения ЛОДУ n-ого порядка с постоянными коэффициентами являются действительными и различными, некоторые являются действительными и совпадающими, некоторые являются различными комплексно сопряженными парами и некоторые совпадающими комплексно сопряженными парами.

Найти общее решение ДУ

.

Характеристическое уравнение этого ЛОДУ с постоянными коэффициентами выглядит так:

.

Многочлен в левой части равенства можно разложить на множители. Из делителей свободного члена вычисляем двукратный корень k₁=k₂=2 и корень k₃=-3. Далее, применяя схему Горнера, приходим к разложению:

.

Из квадратного уравнения находим оставшиеся корни .

Т.о., общее решение заданного ЛОДУ с постоянными коэффициентами выглядит как:

.

🎬 Видео

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

18. Линейные неоднородные дифференциальные уравнения 2 порядка с постоянными коэффициентами. часть 3Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Видеоурок "Нахождение частных решений по виду правой части"Скачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

4. Однородные дифференциальные уравнения (часть 1)Скачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Математика без Ху!ни. Линейные неоднородные дифференциальные уравнения 2 порядка.Скачать