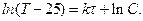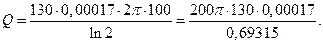Методика составления и решения прикладных задач теории обыкновенных дифференциальных уравнений
Составление дифференциального уравнения по условию задачи (механической, физической, химической или технической) состоит в определении математической зависимости между переменными величинами и их приращениями.
В ряде случаев дифференциальное уравнение получается без рассмотрения приращений — за счет их предварительного учета. Например, представляя скорость выражением 
, мы не привлекаем приращений ∆s и ∆t, хотя они фактически учтены в силу того, что
.
Ускорение в какой-нибудь момент времени t выражается зависимостью:
.
При составлении дифференциальных уравнений приращения сразу же заменяются соответствующими дифференциалами. Изучение любого процесса сводится:
1) к определению его отдельных моментов;
2) к установлению общего закона его хода.
Отдельный момент процесса (т. н. элементарный процесс) выражается уравнением, связывающим переменные величины процесса с их дифференциалами или производными — дифференциальным уравнением; закон общего хода процесса выражается уравнением, связывающим переменные величины процесса, но уже без дифференциалов этих величии.
Исчерпывающих правил для составления дифференциальных уравнений нет. В большинстве случаев методика решения технических задач с применением теории обыкновенных дифференциальных уравнений сводится к следующему:
1.Подробный разбор условий задачи и составление чертежа, поясняющего ее суть.
2.Составление дифференциального уравнения рассматриваемого процесса.
3.Интегрирование составленного дифференциального уравнения и определение общего решения этого уравнения.
4.Определение частного решения задачи на основании данных начальных условий.
5.Определение, по мере необходимости, вспомогательных пара
метров (например, коэффициента пропорциональности и др.),
используя для этой цели дополнительные условия задачи.
6. Вывод общего закона рассматриваемого процесса и число
вое определение искомых величии.
7. Анализ ответа и проверка исходного положения задачи.
Некоторые из этих рекомендаций в зависимости от характера
задачи могут отсутствовать.
Как и при составлении алгебраических уравнений, при решении прикладных задач по дифференциальным уравнениям многое зависит от навыков, приобретаемых упражнением. Однако здесь еще в большей степени требуется изобретательность и глубокое понимание сути изучаемых процессов.
Рассмотрим процесс решения следующих задач:
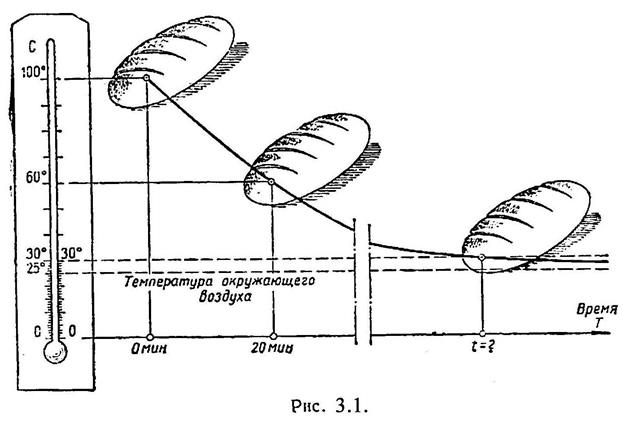
Температура вынутого из печи хлеба в течение 20 мин. падает от 100 0 до 60 0 (рис. 3.1). Температура воздуха равна 25 0 . Через сколько времени от момента начала охлаждения температура хлеба понизится до 30 0 ?
Решение:
В силу закона Ньютона скорость охлаждения тела пропорциональна разности температур тела и окружающей среды. Это – процесс неравномерный. С изменением разности температур в течение процесса меняется также и скорость охлаждения тела. Дифференциальное уравнение охлаждения хлеба будет:
.
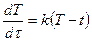
где Т – температура хлеба;
t – температура окружающего воздуха ( в нашем случае 25 0 );
k – коэффициент пропорциональности;
— скорость охлаждения хлеба.
Пусть 
— время охлаждения.
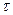
Тогда, разделяя переменные, получим:
,
Видео:Решение физических задач с помощью дифференциальных уравнений. Часть 2Скачать
или для условий данной задачи :
.
Потенцируя обе части последнего равенства, имеем:
,
. (1)
Произвольную постоянную С определяем, исходя из начального условия: при 
мин, Т=100 о .
или С=75.
Величину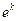 
определяем, исходя из данного дополнительного условия: при 
мин, Т=60 о .
и 
.
Таким образом, уравнение охлаждения хлеба при условиях нашей задачи примет вид:
. (2)
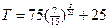
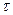
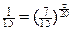
Из уравнения (2) легко определяем искомое время при температуре хлеба Т=30 о :
, или
.
мин.
Итак, после 1 часа 11 мин. Хлеб охлаждается до температуры 30 о С.
Задача 3.2. Трубопровод тепловой магистрали (диаметр 20 см) защищен изоляцией толщиной 10 см; величина коэффициента теплопроводности k=1,00017. Температура трубы 160о; температура внешнего покрова 30о (рис.8). Найти распределение температуры внутри изоляции, а также количество теплоты, отдаваемого одним погонным метром трубы.
Решение. Если тело находится в стационарном тепловом состоянии и температура Т в каждой его точке есть функция только одной координаты х, то согласно закону теплопроводности Фурье количество теплоты, испускаемое в секунду:
, (1)
где F(x)- площадь сечения тела на расстоянии х,
k – коэффициент теплопроводности.
Здесь 
(2)
где l – длина трубы в см,
х – радиус трубопровода в см.
Таким образом, после разделения переменных дифференциальное уравнение примет вид:
(3)
Интегрируя обе части равенства (3), находим:
или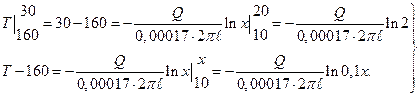 
(4)
Разделив почленно уравнения второе на первое, получим:
.
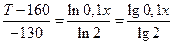
Отсюда закон распределения температуры внутри изоляции:
.
Из первого уравнения системы(4) при 
=100 см имеем:
Количество теплоты, отдаваемое в течение суток, равно
кал.
Занятие по математике (2 курс) Решение задач прикладного характера на составление дифференциальных уравнений
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Решение задач прикладного характера на составление дифференциальных уравнений.
Преподаватель математики Елена Геннадьевна Шерстнева
ЗАНЯТИЕ ПО МАТЕМАТИКЕ ( 2 КУРС)
Решение задач прикладного характера на составление дифференциальных уравнений .
Вид занятия: Применение знаний, умений и навыков полученных при изучении дифференциальных уравнений.
Учебные: показать алгоритм решения задач на составление дифференциальных уравнений, познакомить с математическими моделями в физике, биологии, экономике. Учащиеся должны понимать сущность приложения математики к решению технических задач, которая заключается в том, что задачу переводят на язык математики, решают ее, как принято в математике, и интерпретируют на языке исходных данных.
Воспитательные. Формировать научное мировоззрение. Продолжить знакомить учащихся с понятием математического моделирования, рассказать о том, что одними и теми же дифференциальными уравнениями можно описывать совершенно разные реальные процессы, например электротехнические, механические и другие, т.е. дифференциальные уравнения как математические модели обладают большой общностью и в этом их важное философское и познавательное значение.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
Межпредметные связи. Рассматриваемые на занятии математические модели в физике, биологии, экономике помогут увидеть силу межпредметных связей, важную роль математики, дающей мощный аппарат для решения многих задач, которые выдвигаются и успешно решаются в различных областях науки и практики.
Мотивация познавательной деятельности учащихся. Показать практическую значимость изучаемого материала, его широкое применение в общетехнических и специальных дисциплинах. Многие производственные процессы описываются дифференциальными уравнениями. Поэтому важно не только уметь решать сами дифференциальные уравнения, но и уметь составлять эти уравнения исходя из практической потребности.
Основные знания и умения: иметь понятие о решении несложных задач на составление дифференциальных уравнений по физике, электротехнике, экономике.
Раздаточный материал: Опорный конспект с планом занятия и набором задач для решения.
Технические средства обучения: использование фрагментов из компьютерной программы обучения «Функции и графики», компьютерная презентация конструкторской задачи.
Литература: 1. Валуцэ И.И. Математика для техникумов
2. Соловейчик И.Л. Сборник задач по математике для техникумов
3. Баврин И.И. Начала анализа и математические модели в естествознании и
4. Филимонова Е.В. Математика (среднее профессиональное образование).
Вопросы и упражнения для выполнения на занятии
Какое уравнение называется дифференциальным?
Назовите виды дифференциальных уравнений.
Решите уравнение: 2у dx = (1+ x ) dy . Найти уравнение интегральной кривой, проходящей через точку (1; 4). Задача Коши.
Скорость размножения некоторых бактерий пропорциональна их количеству М в рассматриваемый момент времени t . Найти зависимость количества бактерий от времени. Начальные условия М =М
при t =0
Скорость распада радия пропорциональна его начальному количеству R в данный момент времени t . Найти закон радиоактивного распада. Начальные условия R = R 0 при t =0.
Скорость изменения количества населения прямо пропорциональна этому количеству А на данный период времени. Построить математическую модель прироста (убыли) населения. Начальные условия А = А при t =0.
Решить уравнение: ху ‘ + у = х 
(х ≠ 0).
Инженерно-конструкторская задача. Найти форму автомобильной фары так, чтобы все лучи от зеркала фары шли цилиндрическим световым пучком.
Задача «Истощение ресурсов» В 1980 году для обеспечения пищей одного человека требовалась площадь 0,1 га и на земном шаре было 4000 млн га пахотной земли. Предположим, что с 1980 г эти условия по настоящее время не изменились и не изменятся в будущем, а также не появились и не появятся новые источники пищи. Тогда население Земли должно быть ограничено количеством 40 000 млн человек. Когда будет достигнут этот предел насыщения, если в 1980 году оно составляло 3600 млн человек и непрерывно растет со скоростью 1,7 % в год.
Дополнительные задачи: Скорость прямолинейного движения точки выражается формулой V = 3 + 4 t . Найдите уравнение движения точки, если S = 10 м при t =1 c
Подумайте, какая функция может являться решением уравнения: у » = — k 2 у (уравнение гармонических колебаний). Вторая производная функции равна самой функции с точностью до постоянного множителя.
Запишите домашнее задание №10, 107 учебник И.И. Валуцэ стр.351
«Скорость обесценивания оборудования вследствие его износа в данный момент времени пропорциональна его фактической стоимости ……»
Подведение итогов урока
Математическая модель, основанная на некотором упрощении, никогда не бывает тождественна рассматриваемому объекту, не передает всех его свойств и особенностей, а является его приближенным отражением. Однако, благодаря замене реального объекта соответствующей ему моделью появляется возможность математически сформулировать задачу его изучения и воспользоваться для анализа его свойств математическим аппаратом, который не зависит от конкретной природы данного объекта. Этот аппарат позволяет единообразно описать широкий круг фактов и наблюдений, провести их детальный количественный анализ, предсказать, как поведет себя объект в различных условиях, т.е. прогнозировать результаты будущих наблюдений.
В 1917 году Эйнштейн сделал первую попытку применить общую теорию относительности для описания пространственно временной структуры Вселенной. А основные уравнения теории относительности – это дифференциальные уравнения, имеющие множество решений. Отсюда множество моделей Вселенной.
Дифференциальные уравнения показательного роста (убывания).
Дифференциальные уравнения имеют большое прикладное значение, являясь мощным орудием исследования задач естествознания и техники, они широко используются в механике, астрономии, физике, во многих задачах химии, биологии. Это объясняется тем, что весьма часто объективные законы, которым подчиняются те или иные явления (процессы), записываются в форме дифференциальных уравнений, а сами эти уравнения являются средством для количественного выражения этих законов. Например, законы механики Ньютона позволяют механическую задачу описания движения системы материальных точек или твердого тела свести к математической задаче нахождения решений дифференциальных уравнений. Расчет радиотехнических схем и вычисление траектории спутников, исследование устойчивости самолета в полете и выяснение течения химических реакций – все это производится путем изучения и решения дифференциальных уравнений.
Видео:Решение физических задач с помощью дифференциальных уравненийСкачать
Мы будем рассматривать дифференциальное уравнение вида:
где k – const , причем k может быть : k > 0 или k
Зная формулу производной показательной функции, легко догадаться, что решением этого уравнения, является любая функция вида:
т.к. C – произвольная постоянная, то уравнение имеет бесконечно много решений.
Смысл дифференциального уравнения заключается в том, что скорость изменения функции в точке x пропорциональна значению самой функции в этой точке .
Приведем примеры, в которых величины изменяются по указанному закону .
Если r ‘ ( t ) скорость радиоактивного распада в момент времени t, то скорость уменьшения массы пропорциональна его количеству.
Значит, решением уравнения, является функция r ‘ ( t ) = С e — kt . Найдем из условия, что в начальный момент времени масса радиоактивного вещества была равна:
Промежуток времени T , через который масса радиоактивного вещества уменьшится в 2 раза называют “периодом полураспада”, зная Т , можно найти k :
Логарифмируя по основанию е , получаем — k T = – ln 2 ,
Например, для радия период полураспада 
. Поэтому, 
, следовательно, через 1 млн. лет от начальной массы r o останется.
Задача: Скорость размножения бактерий m ‘ (t) связана с массой m(t) бактерий в момент времени t уравнением:
где k > 0, зависящее от вида бактерий и внешних условий.
Решениями этого уравнения являются функции m ( t ) = C · e kt .
Постоянную C можно найти из условия, что в момент t = 0 масса m o бактерий известна, тогда
Задача. Два тела имеют одинаковую температуру – 100 0 . Они вынесены на воздух, его температура 0 0 . Через 10 мин. температура одного тела стала 80 0 , а второго – 64 0 . Через сколько минут после начала остывания разность их температур будет равна 25 0 .
Значит, 80 0 = 100 0 · e -10 k , e -10 k = 0,8
-10 k = ln 0,8, 
2) 64 0 = 100 0 · 100 0 · e -10 k , тогда e -10 k = 0,64, следовательно -10 k = ln 0,64, 
Следовательно 
Ответ: t = 31,06 мин .
Задача. Задача о гармонических колебаниях.
В практике часто встречаются процессы, которые периодически повторяются например, колебательные движения маятника, струны, пружины, процессы связанные с переменным электрическим током, магнитным полем и т.д. Решение многих таких задач сводится к решению дифференциальных уравнений
где k – заданное положительное число
Инженерно-конструкторская задача. Найти форму автомобильной фары так, чтобы все лучи от зеркала фары шли цилиндрическим световым пучком. (Демонстрация презентации).
1. 
2. 
3. 
4. 
5. 
Решаем квадратное уравнение относительно y’:
следовательно 
Решим это уравнение, взяв + 
, заменяем 
на 
получаем
,умножаем обе части на dx , отсюда 
это однородное уравнение.
Сделаем замену y = z x и продифференцируем ее по x, получим dy = x dz + z dx , подставляем 
Обе части делим на x получаем 
, раскрываем скобки и приводим подобные 
, разделяем переменные 
, интегрируем 
, решением будет функция 
далее 
, т.к 
, то 
раскрываем скобки 
в итоге получаем 
— это каноническое уравнение параболы с вершиной (
; 0) и фокусом в точке (0;0).
Задача «Истощение ресурсов» В 1980 году для обеспечения пищей одного человека требовалась площадь 0,1 га и на земном шаре было 4000 млн га пахотной земли. Предположим, что с 1980 г эти условия по настоящее время не изменились и не изменятся в будущем, а так же не появились и не появятся новые источники пищи. Тогда население Земли должно быть ограничено количеством 40 000 млн человек. Когда будет достигнут этот предел насыщения, если в 1980 году оно составляло 3600 млн человек и непрерывно растет со скоростью 1,7 % в год.
Решение. А = А0 e к t
А0 = 3,6 · 10 9 , А = 40 · 10 9 , k = 0,017
40 · 10 9 = 3,6 · 10 9 · e 0,017t , t = (2 ln 10/3) /0,017 ≈ 142 г.
Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать
Ответ: В 2122 году наступит предел насыщения
Беседа о бережном отношении к природе и ее богатствам.
💡 Видео
Урок 323. Применение производной в задачах физики - 1Скачать
Решение физических задач при помощи диффуров | Дифференциальные уравненияСкачать
2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
Дифференциальные уравнения в решениях физических задач БЕЗ ДЯДИ КОЛИ (100)Скачать
Операторный метод решения дифференциальных уравнений | Решение задачСкачать
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать
14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать
Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать
Линейное неоднородное дифференциальное уравнение 2 способаСкачать
Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать
