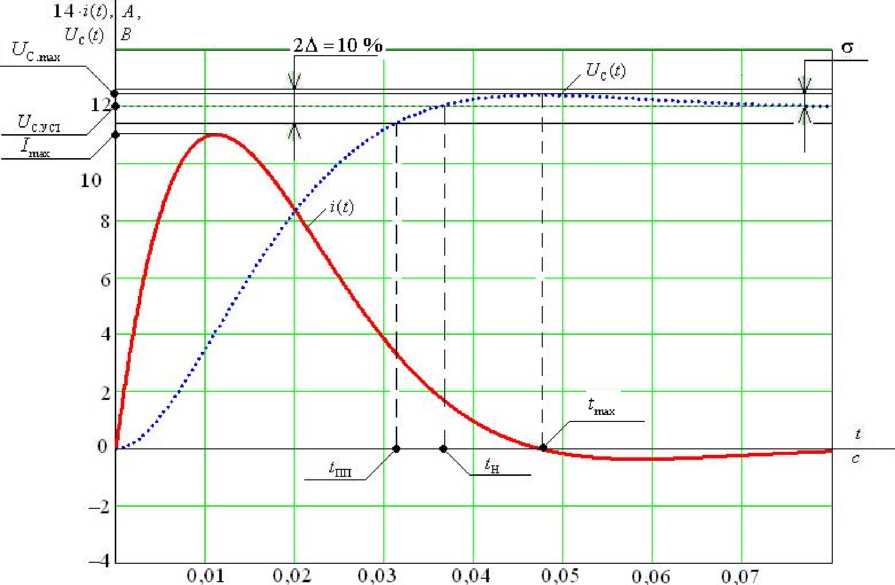
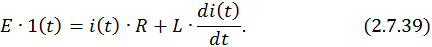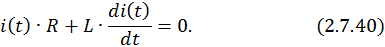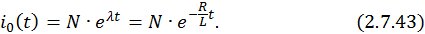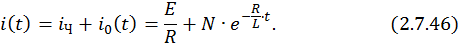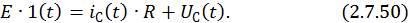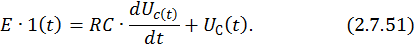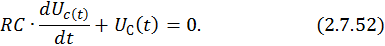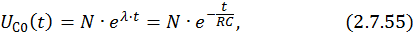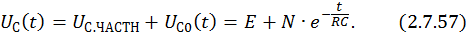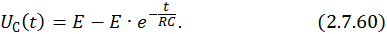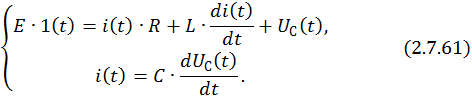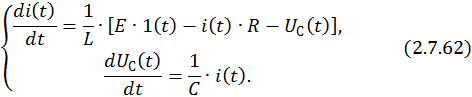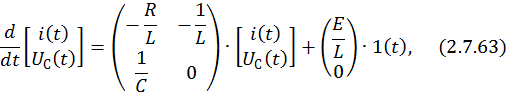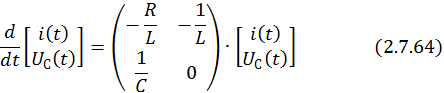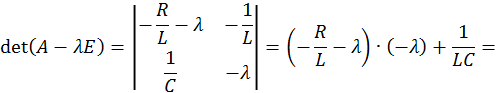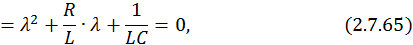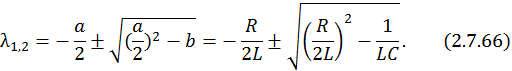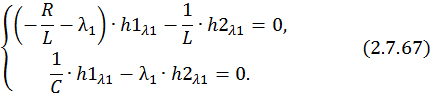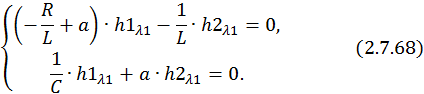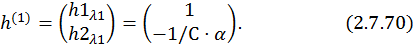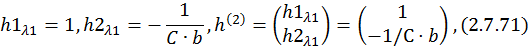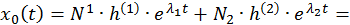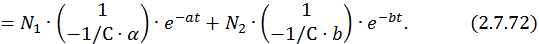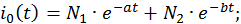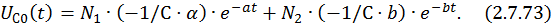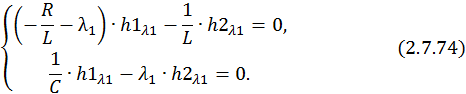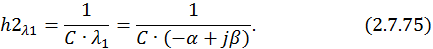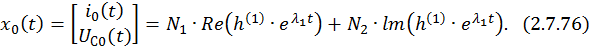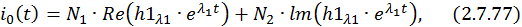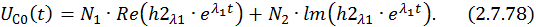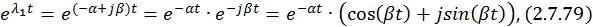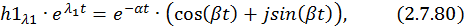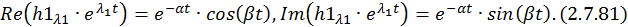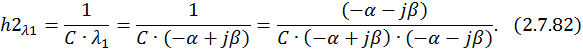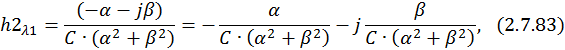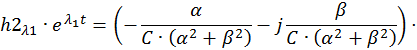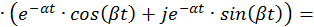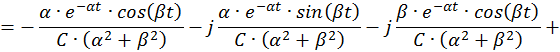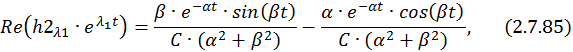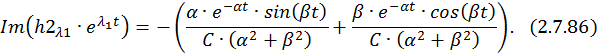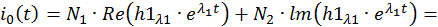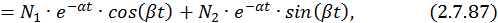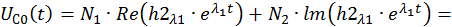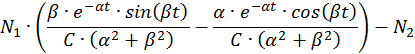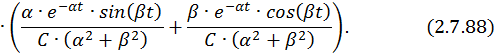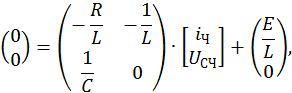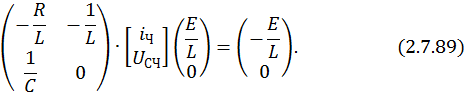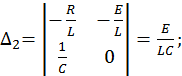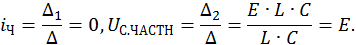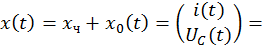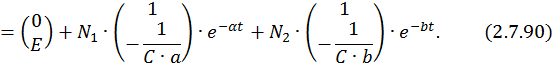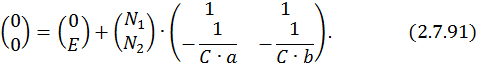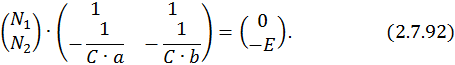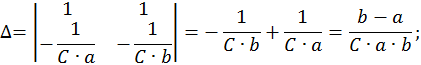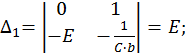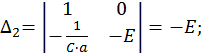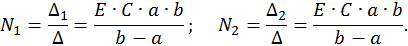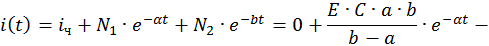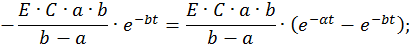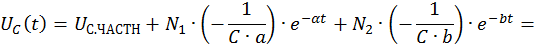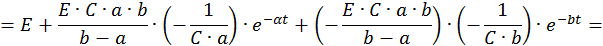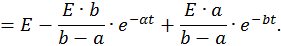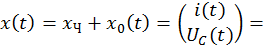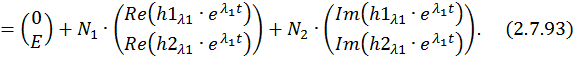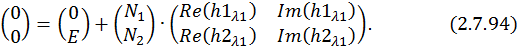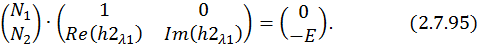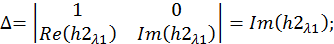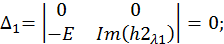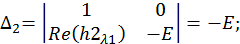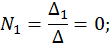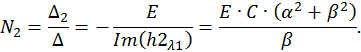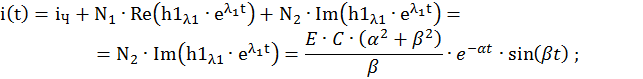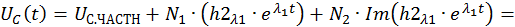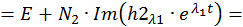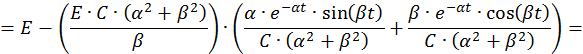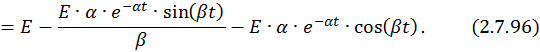Переходные процессы в цепи R, L, C описываются дифференциальным уравнением 2-го порядка. Установившиеся составляющие токов и напряжений определяются видом источника энергии и определяются известными методами расчета установившихся режимов. Наибольший теоретический интерес представляют свободные составляющие, так как характер свободного процесса оказывается существенно различным в зависимости от того, являются ли корни характеристического уравнения вещественными или комплексными сопряженными.
Проанализируем переходной процесс в цепи R, L, C при включении ее к источнику постоянной ЭДС (рис. 70.1).
Общий вид решения для тока: i(t)=iy(t)+iсв(t)=Iy+A1ep2t+A2ep2t
Установившаяся составляющая: Iy=0
Характеристическое уравнение и его корни:
Независимые начальные условия: i(0)=0; uc(0)=0.
Зависимое начальное условие:
Постоянные интегрирования определяется из соместного решения системы уравнений:
Окончательное решение для тока:
Исследуем вид функции i(t) при различных значениях корней характеристического уравнения.
а) Корни характеристического уравнения вещественные, не равны друг другу.
Это имеет место при условии:

При изменении t от 0 до ∞ отдельные функции ep1t и ep2t убывают по экспоненциальному закону от 1 до 0, причем вторая из них убывает быстрее, при этом их разность ep1t — ep2t ≥ 0. Из этого следует вывод, что искомая функция тока i(t) в крайних точках при t = 0 и при t = ∞ равна нулю, а в промежутке времени 0
Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

4.4. Переходные процессы в RLC-цепях
Видео:Составление дифференциального уравненияСкачать

4.4. Переходные процессы в RLC-цепях
Рассмотрим переходные процессы в RLC-цепях на примере цепи последовательного колебательного контура рис. 4.3,а, потери в котором будем учитывать путем включения в цепь резистораR.
Рис.4.3. RLC-цепь (а) и переходные процессы в ней (б) и (в).
Переходные процессы в последовательном колебательном контуре при нулевых начальных условиях. Установим ключ К в положение 1, и подключим входное воздействие к контуру. Под действием подключенного источника u в контуре потечет ток i, который создаст напряжения uR, uL, uC .
На основании второго закона Кирхгофа для этого контура можно записать следующее уравнение

Учитывая, что 

Общее решение уравнения (4.34) будем искать в виде суммы свободной uС св и принужденной uС пр составляющих:

Свободная составляющая определяется решением однородного дифференциального уравнения, которое получается из (4.34) при u = 0

Решение (4.36) зависит от корней характеристического уравнения, которое получается из (4.36) и имеет вид

Корни этого уравнения определяются только параметрами цепи R, L ,C и равны

где α = R/2L – коэффициент затухания контура;

Из (4.38) видно, что корни р1 и р2 зависят от характеристического сопротивления контура 
при R > 2ρ вещественными и различными;
при R 2ρ свободная составляющая будет равна:

Пусть входное воздействие u = U = const, тогда принужденная составляющая uпр = U. Учитывая выражение (4.39) и что uпр = U выражение (4.35) примет вид:

Зная uС находим ток в контуре

Для определения постоянных интегрирования А1 и А2 запишем начальные условия для uC и i при t = 0:

Решая систему уравнений (4.42) получаем:


Подставляя А1 и А2 в уравнения (4.40) и (4.41) и учитывая, что в соответствии с (4.38) p1 p2=1/LC будем иметь:


Так как 

Графики изменения uС, i, uL в последовательном колебательном контуре при условии R > 2ρ приведены на рис. 4.3,б).
Моменты времени t1 и t2 определяются соответственно из условий



Анализ графиков, описываемых выражениями (4.43 – 4.45) показывает, что при R > 2ρ (при больших потерях) в контуре происходят апериодические процессы.
Рассмотрим процессы в контуре при R 2ρ, то корни р1 и р2 в (4.38) будут вещественны и различны и решение уравнения (4.36) будет иметь вид

Напряжение uC создает ток в цепи

Для определения постоянных интегрирования А1 и А2 положим t = 0 и учтем, что на момент коммутации uC = U, i = 0, тогда из (4.54) и (4.55) получим

Решая систему уравнений (4.56) находим


Подставляя А1 и А2 в (4.54) и (4.55) получаем уравнения для напряжения uC и тока i в цепи контура


Из выражений (4.57) и (4.58) видно, что при отключении входного воздействия от цепи контура, который имеет большое затухание (R > 2ρ) происходит апериодический разряд емкости С. Запасенная до отключения входного воздействия энергия в емкости WС = CU2/2 расходуется на покрытие тепловых потерь в резисторе R и создания магнитного поля в индуктивности L. Затем энергия электрического поля емкости WС и магнитная энергия индуктивности WL расходуется в резисторе R.
Найдем закон изменения напряжения uC и тока i в цепи, когда контур обладает малыми потерями, т.е. при условии R
Видео:2020 г. Дифференциальные уравнения для электрических цепей. Лекция и практикаСкачать

Решение дифференциальных уравнений на примере RLC- цепей
Решения дифференциального уравнения на примере RL-цепи.Схема коммутации RL-цепи на источник постоянного напряжения представлена на рис. 2.40.
Рис. 2.41. Схема коммутации RL -цепи на источник постоянного напряжения
Процессы, протекающие в цепи при замыкании ключа, описываются дифференциальным уравнением 1-го порядка, составленным по второму закону Кирхгофа:
Характеристическое уравнение получается из однородного ДУ для переменной 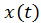
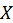
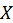
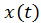
Однородное дифференциальное уравнение –
Определим корень характеристического уравнения –
Общее решение i0(t) однородного уравнения –
Для нахождения частного решения неоднородного ДУ подставим в исходное уравнение значение t = ∞. Тогда оно будет выглядеть следующим образом:
Общее решение неоднородного уравнения –
Решим задачу Коши с нулевыми начальными условиями. Для этого подставим в общее решение неоднородного ДУ значение 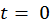
откуда постоянная интегрирования
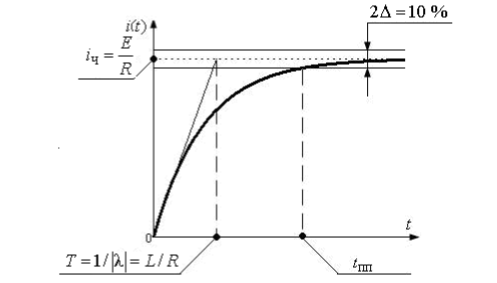
В итоге временная зависимость тока в RL -цепи при коммутации ее на источник постоянного напряжения
Графическое решение ДУ представлено на рис. 2.42:
Рис. 2.42. Изменение тока в RL-цепи при коммутации на источниках постоянного напряжения
На графике обозначена также постоянная времени цепи Т, обратная модулю корня характеристического уравнения 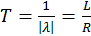
Решения дифференциального уравнения на примере RС-цепи.Схема коммутации RC-цепи на источник постоянного напряжения представлена на рис. 2.43.
Рис. 2.43. Схема коммутации RC-цепи на источник постоянного напряжения Е
Дифференциальное уравнение, составленное по второму закону Кирхгофа, описывает процессы в цепи после замыкания ключа:
Учитывая, что 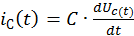
Найдем общее решение однородного уравнения:
Определим корень характеристического уравнения:
Общее решение 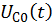
Для нахождения частного решения неоднородного ДУ подставим в исходное уравнение значение t =∞. Тогда оно будет выглядеть следующим образом:
Общее решение неоднородного уравнения –
Решим задачу Коши с нулевыми начальными условиями. Для этого подставим в общее решение неоднородного ДУ значение t = 0. Получим
откуда постоянная интегрирования
В итоге временная зависимость тока в RC-цепи при коммутации ее на источник постоянного напряжения
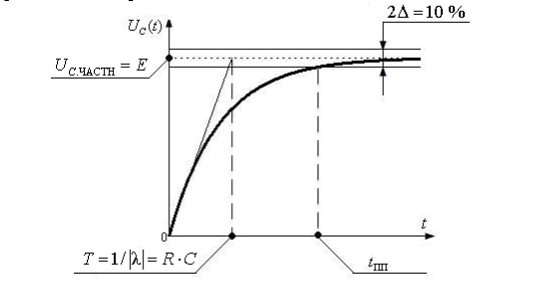
Графическая зависимость напряжения на конденсаторе от времени представлена на рис. 2.44.
Рис. 2.44. Изменение напряжения на конденсаторе при коммутации на источник постоянного напряжения
На графике обозначена также постоянная времени цепи Т, обратная модулю корня характеристического уравнения 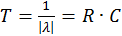
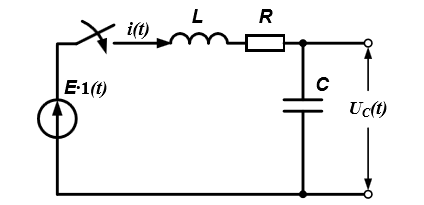
Решения системы дифференциальных уравнений на примере RLC-цепи.Коммутация RLC-цепи на источник постоянного напряжения представлена на рис. 2.45.
Рис. 2.45. Схема коммутации RLC-цепи на источник постоянного напряжения
Составим СДУ по первому и второму законам Кирхгофа:
Представим СДУ в нормальной форме Коши:
Запишем СДУ в матричной форме:
где 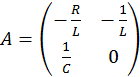
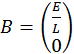
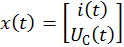
Однородная СДУ, соответствующая неоднородной СДУ, –
Найдем собственные значения матрицы A, составив характеристическое уравнение 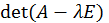
Это уравнение вида λ 2 + а 
Предположим, что корни характеристического уравнения действительные, различные: λ1 = –a, λ2 = –b, где a и b – неотрицательные числа. Отметим также, что для устойчивости динамической системы необходимо, чтобы действительные части корней характеристического уравнения были отрицательными.
Найдем собственные вектора для каждого собственного значения матрицы A. Для значения λ1 = –a алгебраическая система уравнений будет выглядеть следующим образом:
Примем значение 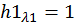
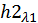
Собственный вектор для первого собственного значения матрицы A –
Аналогично будет находиться собственный вектор и для второго собственного значения матрицы A:
Общее решение СДУ 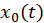
Можно записать отдельно выражения для каждой временной функции:
Предположим, что корни характеристического уравнения комплексно сопряженные: λ1,2 = –α ± jβ, где α и β – неотрицательные числа. В этом случае собственный вектор ищется только для одного из этих значений.
Найдем собственный вектор для λ1 = –α + jβ:
Принимаем 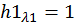
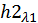
Общее решение однородной СДУ в этом случае запишется в виде
Запишем каждую компоненту общего решения отдельно:
Найдем составляющие общего решения однородной СДУ. По формуле Эйлера для комплексных чисел
Для разделения вещественной и мнимой частей второй составляющей 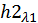
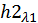
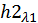
Учитывая формулу умножения комплексно сопряженных чисел друг на друга, запишем:
Общее решение однородной СДУ:
Как видно, при действительных корнях общее решение однородной СДУ включает в себя только экспоненты, а при комплексно сопряженных корнях еще и синусные и косинусные составляющие. В первом случае переходные процессы в ЭМС имеют апериодический характер, а во втором случае – затухающий колебательный.
Найдем частное решение неоднородной СДУ при подстановке в исходную СДУ значения 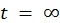
Найдем решение этой СЛАУ методом Крамера:
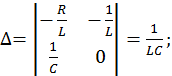
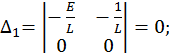
Полученное частное решение неоднородной СДУ легко объясняется физически – конденсатор заряжается до напряжения источника питания E, а ток в цепи после окончания переходного процесса становится равным нулю, так как при работе на постоянном токе конденсатор представляет собой разрыв цепи.
Следующим этапом является нахождение постоянных времени путем подстановки в общее решение неоднородной СДУ значения t = 0 и последующего решения получившейся СЛАУ. Решим задачу Коши для обоих случаев собственных значений матрицы A – действительных и комплексно-сопряженных.
Найдем постоянные интегрирования при действительных отрицательных собственных значениях матрицы A: λ1 = –a, λ2 = –b. Общее решение неоднородной СДУ в этом случае имеет вид
Подставим в это выражение значение времени 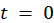
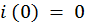
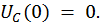
Перенесем свободные члены:
Решим эту СЛАУ методом Крамера:
Запишем компоненты общего решения неоднородной СДУ:
Определим постоянные интегрирования при комплексно–сопряженных корнях характеристического уравнения: λ1,2 = –α ± jβ. Общее решение неоднородной СДУ имеет в этом случае следующий вид:
Подставим в это выражение значение времени 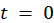
Перенесем свободные члены, а также учтем, что 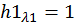
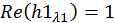
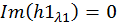
Решим эту СЛАУ методом Крамера:
Запишем компоненты общего решения СДУ:
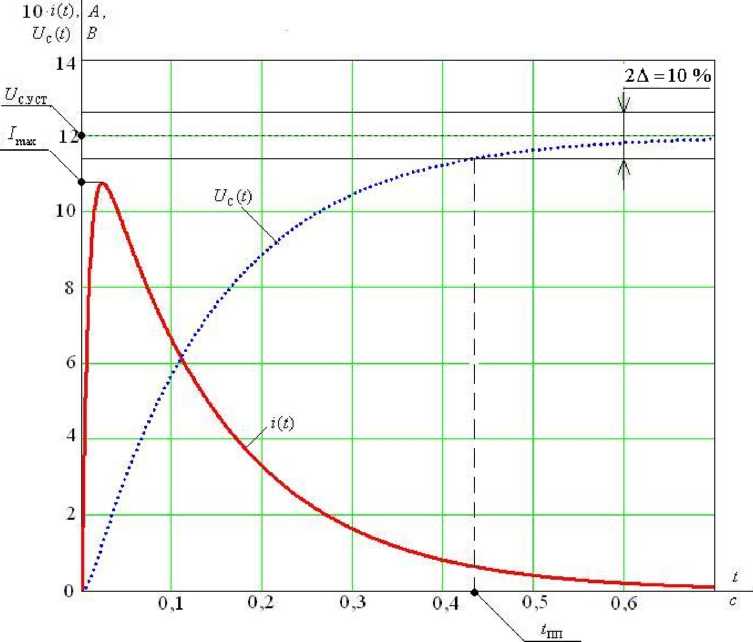
Графические решения СДУ при разных случаях корней характеристического уравнения показаны на рис. 2.46 и 2.47 соответственно.
Рис. 2.46.Переходные процессы в RLC-цепи при действительных корнях характеристического уравнения
Рис. 2.47.Переходные процессы в RLC-цепи при комплексно-сопряженных корнях характеристического уравнения
Дата добавления: 2021-01-26 ; просмотров: 443 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
🎦 Видео
Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Решение задачи Коши в MathCADСкачать

Урок 17. Как работает Интегрирующая и Дифференцирующая RC-цепь | Самое понятное объяснениеСкачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Пример 7 | Классический метод расчета цепи 1-го порядка с конденсаторомСкачать

5 Численное решение дифференциальных уравнений Part 1Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Пример 6 | Классический метод расчета цепи первого порядка с конденсаторомСкачать

Линейные цепи и элементы. Дифференциальные уравнения для цепейСкачать

Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Пример 1. Операторный метод расчета цепи первого порядка с катушкойСкачать

Частное решение ДУ, с помощью рядаСкачать