Типовые динамические звенья- это минимально необходимый набор звеньев для описания системы управления произвольного вида.
Типы звеньев систем управления различаются по виду их передаточной функции (или дифференциального уравнения), определяющей все их динамические свойства и характеристики. Классификация основных типов динамических звеньев приведена на рис.3.9.
Основные типы звеньев делятся на четыре группы: позиционные, интегрирующие, дифференцирующие и неминимально-фазовые [1,2]. Позиционные, интегрирующие и дифференцирующие звенья относятся к минимально-фазовым. Важным свойством минимально-фазовых звеньев является однозначное соответствие амплитудной и фазовой частотных характеристик. Другими словами, по заданной амплитудной характеристике всегда можно определить фазовую и наоборот.
Позиционные звенья
В звеньях позиционного, или статического типа, линейной зависимостью y = kx связаны выходная и входная величины в установившемся режиме. Коэффициент пропорциональности k между выходной и входной величинами представляет собой коэффициент передачи звена. Позиционные звенья обладают свойством самовыравнивания, то есть способностью самостоятельно переходить в новое установившееся состояние при ограниченном изменении входного воздействия.

Безынерционное (идеальное усилительное) звено.Это звено не только в статике, но и в динамике описывается алгебраическим уравнением
Амплитудно-фазовая частотная характеристика:
W(jw) = k, A(w) = k, y(w) = 0. (3.16)
Переходная и импульсная функции:
h(t) = k1(t), w(t) = kd(t). (3.17)
Безынерционное звено является некоторой идеализацией реальных звеньев. В действительности ни одно звено не в состоянии равномерно пропускать все частоты от 0 до ¥.
Примерами таких безынерционных звеньев могут служить жесткая механическая передача, часовой редуктор, электронный усилитель сигналов на низких частотах и др.
Апериодическое (инерционное) звено первого порядка.Уравнение и передаточная функция звена:
(Tp+1) y(t) = x(t), 
где T — постоянная времени, характеризует степень инерционности звена, т.е. длительность переходного процесса.
Амплитудно-фазовая частотная характеристика:
W(jw) = 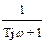

Таким образом, апериодическое звено первого порядка является фильтром низких частот.
Переходная и импульсная функции:
h(t) = (1 — 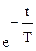

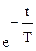
Примерами апериодического звена первого порядка могут служить RC цепочка, нагревательный элемент и др.
Апериодическое (инерционное) звено второго порядка.Дифференциальное уравнение звена имеет вид

причем предполагается, что 2Т2£ Т1.
В этом случае корни характеристического уравнения вещественные и уравнение (3.21) можно переписать в виде:
где 
Передаточная функция звена

Из выражения (3.23) следует, что апериодическое звеновторого порядка можно рассматривать как комбинацию двух апериодических звеньев первого порядка.
Примерами апериодического звена второго порядка могут служить двойная RC цепочка, электродвигатель постоянного тока и др.
Колебательное звено.Описывается дифференциальным уравнением

при Т1 2 p 2 +2xTp+1) y(t) = x(t), (3.25)
где Т — постоянная времени, определяющая угловую частоту свободных колебаний l=1/Т;
x — параметр затухания, лежащий в пределах 0
Амплитудно-фазовая характеристика совпадает с вещественной осью. При 0 1/T — с отрицательной полуосью.
Временные характеристики соответствуют незатухающим колебаниям с угловой частотой 1/T.
Интегрирующие звенья
В звеньях интегрирующего типа линейной зависимостью 

Идеальное интегрирующее звено.Уравнение и передаточная функция имеют вид
py(t) = x(t), 
Амплитудно-фазовая частотная характеристика:
W(jw) = 

Переходная и импульсная функции:
h(t) = t, w(t) = 1(t). (3.30)
Такое звено является идеализацией реальных интегрирующих звеньев.
Примерами идеальных интегрирующих звеньев могут служить операционный усилитель в режиме интегрирования, гидравлический двигатель, емкость и др.
Дифференцирующие звенья
В звеньях дифференцирующего типа линейной зависимостью 
Идеальное дифференцирующее звено.Уравнение и передаточная функция имеют вид
y(t) = px(t), W(s) = s . (3.31)
Амплитудно-фазовая частотная характеристика:
W(jw) = jw, A(w) = w, y(w) = +90 0 . (3.32)
Переходная и импульсная функции:
h(t) = d(t), w(t) = 
Такое звено является идеализацией реальных дифференцирующих звеньев.
Примерами идеальных дифференцирующих звеньев могут служить операционный усилитель в режиме дифференцирования, тахогенератор и др.
Форсирующее (дифференцирующее) звено первого порядка.Дифференциальное уравнение и передаточная функция
y(t) = (tp+1) x(t) , W(s) = ts+1, (3.34)
где t — постоянная времени дифференцирования.
Амплитудно-фазовая частотная характеристика:
W(jw) = (jwt + 1), A(w)= 
Переходная и импульсная функции:
h(t) = 1(t) + td(t), w(t) = d(t) + t 
Форсирующее (дифференцирующее) звено второго порядка.Уравнение и передаточная функция звена:
y(t) = (t 2 p 2 +2xtp+1)x(t), W(s) = t 2 s 2 +2xts+1. (3.37)
Амплитудно-фазовая частотная характеристика:
W(jw) = (1-w 2 t 2 ) + j2xwt,
A(w)= 

Переходная и импульсная функции:
h(t) = t 2 


Видео:Типовые динамические звенья | Вечер с теорией управления, вебинар 3Скачать

Типовые динамические звенья
Типовым динамическим звеном САУ является составная часть системы, которая описывается дифференциальным уравнением не выше второго порядка. Звено, как правило, имеет один вход и один выход. По динамическим свойствам типовые звенья делятся на следующие разновидности: позиционные, дифференцирующие и интегрирующие.
Позиционными звеньями являются такие звенья, у которых в установившемся режиме наблюдается линейная зависимость между входными и выходными сигналами. При постоянном уровне входного сигнала сигнал на выходе также стремится к постоянному значению.
Дифференцирующими являются такие звенья, у которых в установившемся режиме выходной сигнал пропорционален производной по времени от входного сигнала.
Интегрирующими являются такие звенья, у которых выходной сигнал пропорционален интегралу по времени от входного сигнала.
Звено считается заданным и определенным, если известна его передаточная функция или дифференциальное уравнение. Кроме того, звенья имеют временные и частотные характеристики.
Наличие нулевых корней в числителе или знаменателе ПФ типовых звеньев — это признак для разбиения последних на три группы:
Позиционные звенья: 1, 2, 3, 4, 5, — не имеют нулевых корней, и, следовательно, в области низких частот (т.е. в установившемся режиме), имеют коэффициент передачи равный k.
Интегрирующие звенья: 6, 7, 8, — имеют нулевой корень-полюс, и, следовательно, в области низких частот, имеют коэффициент передачи, стремящийся к бесконечности.
Дифференцирующие звенья: 9, 10 — имеют нулевой корень-ноль, и, следовательно, в области низких частот, имеют коэффициент передачи, стремящийся к нулю.
| 6.2. Типы объектов и законы регулирования |
В зависимости от величины самовыравнивания различают три типа объектов управления: устойчивый (с положительным самовыравниванием); нейтральный (с нулевым самовыравниванием); неустойчивый (с отрицательным самовыравниванием). Признаком отрицательного самовыравнивания является отрицательный знак перед самой выходной величиной в левой части дифференциального уравнения или появление отрицательного знака у свободного члена знаменателя передаточной функции (наличие положительного полюса).
Под законом регулирования (управления) понимается алгоритм или функциональная зависимость, определяющая управляющее воздействие u(t) на объект:
u(t) = F(Δ) , где Δ — ошибка регулирования.
Законы регулирования бывают:
— линейные: 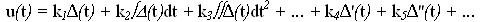
или 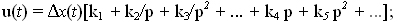
— нелинейные: 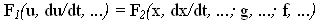
Кроме того, законы регулирования могут быть реализованы в непрерывном виде или в цифровом. Цифровые законы регулирования реализуются путем построения регуляторов с помощью средств вычислительной техники (микро ЭВМ или микропроцессорных систем).
Наличие в (3.1) чувствительности регулятора к пропорциональной, к интегральным или к дифференциальным составляющим в первичной информации x(t), определяет тип регулятора:
1. P — пропорциональный;
2. I — интегральный;
3. PI — пропорционально интегральный (изодромный);
4. PD — пропорционально дифференциальный;
5. и более сложные варианты — PID, PIID, PIDD, .
Нелинейные законы регулирования подразделяются на:
1. функциональные;
2. логические;
3. оптимизирующие;
4. параметрические.
В составе структуры САУ содержится управляющее устройство, которое называется регулятором и выполняет основные функции управления, путем выработки управляющего воздействия U в зависимости от ошибки (отклонения), т.е. U = f(Δ). Закон регулирования определяет вид этой зависимости без учёта инерционности элементов регулятора. Закон регулирования определяет основные качественные и количественные характеристики систем.
| 6.4. Временные характеристики звеньев САУ |
Важнейшей характеристикой САР и её составных элементов являются переходные и импульсные переходные (импульсные) функции.
Аналитическое определение переходных функций и характеристик основано на следующих положениях. Если задана передаточная функция системы или отдельного звена W(р) и известен входной сигнал X(t), то выходной сигнал Y(t) определяется следующим соотношением:
Таким образом, изображение выходного сигнала 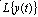
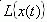
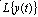
Так как изображение единичного ступенчатого воздействия равно 1/p, то изображение переходной функции определяется соотношением:
Следовательно, для нахождения переходной функции необходимо передаточную функцию разделить на p и выполнять переход от изображения к оригиналу.
Изображение единичного импульса равно 1. Тогда изображение импульсной функции определяется выражением:
Таким образом, передаточная функция является изображением импульсной функции.
Импульсная и переходная функции, как и передаточная функция, являются исчерпывающими характеристиками системы при нулевых начальных условиях. По ним можно определить выходной сигнал при произвольных входных воздействиях.
Таблица 3.1
Изображение по Лапласу и оригиналы
Изображение 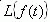 | Оригинал f(t) |
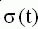 | |
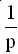 | 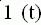 |
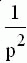 | 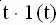 |
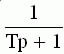 | 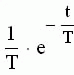 |
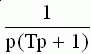 | 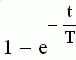 |
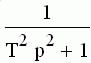 | 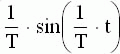 |
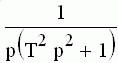 | 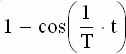 |
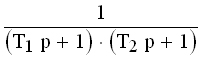 | 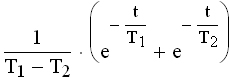 |
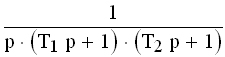 | 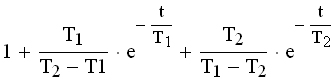 |
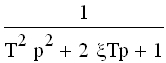 | 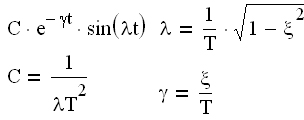 |
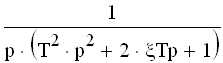 | 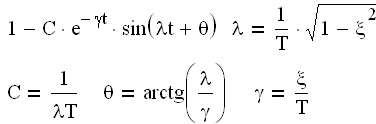 |
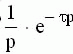 | 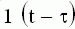 |
Передаточные функции и временные характеристики типовых звеньев приведены в таблице 3.2.
Таблица 3.2
Временные характеристики типовых звеньев
| Тип звена | Передаточные функции | Временные функции | |||
| Позиционные звенья | |||||
| Усилительное | 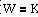 | 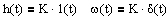 | |||
| Апериодическое 1-го порядка | 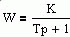 | 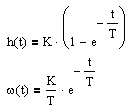 | |||
| Апериодическое 2-го порядка T1≥2T2 | 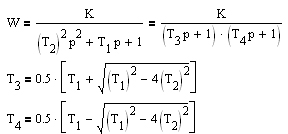 | 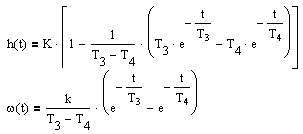 | |||
| Колебательное 0 jφ(ω) (3.2) , где Функция A(ω), представленная при изменении частоты от 0 до
Дата добавления: 2016-03-20 ; просмотров: 7279 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ Видео:10) ТАУ для чайников Части 4.1. и 4.2. Типовые динамические звенья. Усилитель. Апериодическое звено.Скачать  Апериодическое (инерционное, статическое) звено. Передаточная функция и уравненияДифференциальное уравнение, описывающее взаимосвязь входного и выходного сигналов апериодического типового динамического звена (ТДЗ), можно представить в следующем виде: Где: k – коэффициент передачи, Т0 – постоянная времени. Дифференциальное уравнение является не самой удобной формой представления математической модели объекта или звена. Это связано с тем, что решения любого дифференциального уравнения довольно сложная вычислительная процедура. Более удобна и, соответственно чаще используемая, математическая модель объекта, записанная в виде передаточной функции. Передаточная функция – это преобразованное по Лапласу исходное дифференциальное уравнение, то есть уравнение, записанное в виде преобразованных по Лапласу выходного и входного сигналов объекта (звена). Исходное дифференциальное уравнение в преобразовании Лапласа называют оригиналом, а записанное в операторной форме преобразованное уравнение – его изображением. Суть преобразования Лапласа заключается в замене на функции комплексных переменных Хвых(р) и Хвх(р) функций вещественных переменных Хвых(τ) и Хвх(τ), где р – оператор Лапласа (комплексное число р = ±m±in). Данные функции связываются между собой интегралом Лапласа: Для большинства используемых в ТДЗ дифференциальных уравнений, чисто формальным условием перехода от оригинала к изображению будут представленные ниже замены: Использовав приведенное выше условие довольно легко получить изображение, то есть перейти к операторной форме записи дифференциального уравнения апериодического звена. Оригинал дифференциального уравнения апериодического звена имеет следующий вид: Операторная форма записи (изображения) уравнения апериодического звена: Огромным преимуществом данного преобразования является то, что записанное в операторной форме исходное дифференциальное уравнения становится алгебраическим. Но стоит отметить, что если бы все дифференциальные уравнения можно было бы преобразовать по Лапласу, то в математике произошла бы революция, так как решение алгебраических уравнение значительно проще дифференциальных. К сожалению, такое преобразование возможно лишь для ограниченного количества уравнений, в том числе для уравнений типовых динамических звеньев (ТДЗ). Поскольку уравнение апериодического звена приняло вид алгебраического, то его можно записать следующим образом: Из полученного выражения достаточно легко выделить отношение Хвых(р) / Хвх(р), которое называется передаточной функцией и для апериодического звена имеет вид: У каждого типового динамического звена присутствует ряд типовых частотных характеристик: амплитудно-частотную (АЧХ), фазочастотную (ФЧХ), амплитудно-фазовую частотную (АФЧХ или АФХ), логарифмическую амплитудно-частотную (ЛАЧХ), логарифмическую фазочастотную (ЛФЧХ). На практике чаще всего используется АФЧХ или АФХ. Амплитудно-фазовая характеристика это вектор, а график АФХ – годограф этого вектора, то есть кривая на комплексной плоскости, которую описывает конец вектора при изменении частоты ω от 0 до ∞. Вектор характеризуется двумя величинами – длина (скаляр или вектор по модулю) и направление (градиент). Вектор аналитически можно записать в виде двух проекций на действительную и мнимую оси, и выразить эти проекции через угол α: После использования формулы Эйлера: Где |W| — длина вектора или вектор по модулю, i – мнимое число: Аналитическое выражение для любого вектора АФХ любого типичного динамического звена легко получить из передаточной функции, заменив в ней оператор Лапласа р на выражение iω. Где ω – частота колебаний (ω = 2π/Т), Т – период колебаний. Для апериодического звена амплитудно-фазовая частотная характеристика (АФХ) имеет вид: Для записи вектора АФХ в виде проекций на действительную и мнимую ось необходимо произвести следующие преобразования: Изменяя частоту ω от 0 до ∞ можно построить на комплексной плоскости годораф (график вектора АФХ), представляющий из себя полуокружность (рисунок а)), которая располагается в четвертом квадранте комплексной плоскости. Диаметр полуокружности равен коэффициенту k. На рисунке б) показана типовая переходная функция апериодического звена. Как видно из графика, она изменяется по экспоненциальному закону. У любой экспоненты есть одно прекрасное свойство – если к любой ее точке провести касательную, а затем точку пересечения касательной с асимптотой и точку касания спроецировать на ось времени, то получится один и тот же отрезок времени на оси времени. Эта проекция, которую называют постоянной времени, соответствует значению коэффициента Т0 в АФХ и передаточной функции апериодического звена, а ордината асимптоты, к которой стремится экспонента, соответствует коэффициенту k в передаточной функции. Таким образом, по переходной характеристике апериодического звена довольно легко найти коэффициенты Т0 и k в передаточной функции звена. Физическим примером апериодического звена может быть конденсатор, при подаче напряжения на который заряд происходит не мгновенно, а с определенной задержкой, или же электродвигатель, который при подаче питания разгоняется не мгновенно, а через какое-то время t. На рисунке в) показан пример установки, которую также можно считать апериодическим звеном (вода – заполняющая бак). В бак поступает определенное количество воды с расходом Q1. В то же время из бака вытекает вода с расходом Q2. Регулируемый параметр в этой системе Хвых – уровень воды в баке H. При подаче единичного скачка Q1 (открыли входной вентиль) уровень воды H в баке повышается. При этом растет гиростатическое давление и возрастает Q2. Через некоторое время уровень воды H в баке стабилизируется (экспонента приближается к асимптоте). Способность самостоятельно восстанавливать равновесие, которое присуща объектам, аппроксимируемым апериодическим звеном, за счет стока или притока вещества или энергии называют самовыравниванием. Количество самовыравнивания определяет коэффициент р, равный обратному значению коэффициента k в передаточной функции звена, то есть р = 1/k. В литературе объекты с передаточной функцией апериодического звена называют статическими. 📽️ ВидеоТеория автоматического управления. Лекция 7. Типовые звенья САУСкачать  12) ТАУ для чайников. Часть 4.4. Интегрирующее звено.Скачать  Видеометодичка. Практикум по нахождению передаточных функций по дифференциальным уравнениямСкачать  c04 3, Динамические звенья 2: типовые звенья и их АФЧХСкачать  11)ТАУ для чайников. Часть 4.3. Колебательное звеноСкачать  Типовые звеньяСкачать  Откуда появляются дифференциальные уравнения и как их решатьСкачать  Решение физических задач с помощью дифференциальных уравненийСкачать  16) ТАУ для чайников. Часть 4.8. ЛАФЧХ сложных звеньевСкачать  proТАУ: 2. Типовые звеньяСкачать  c04 2, Динамические звенья 2: классификация звеньевСкачать  Линейное неоднородное дифференциальное уравнение 2 способаСкачать  c03 7, Динамические звенья 1: передаточная функцияСкачать  Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать  Дифференциальные уравнения. 11 класс.Скачать  |
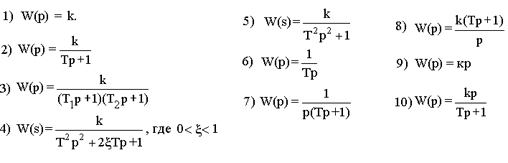
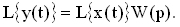
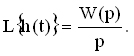
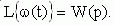
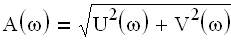 — модуль;
— модуль; 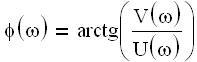 — аргумент частотной передаточной функции.
— аргумент частотной передаточной функции.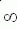 получило название амплитудной частотной характеристики (АЧХ).
получило название амплитудной частотной характеристики (АЧХ). 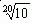 раз. Верхняя полуплоскость л.а.х. соответствует значениям А>1 (усиление амплитуды), а нижняя полуплоскость — значениям А 0, r>0, T>0, 0
раз. Верхняя полуплоскость л.а.х. соответствует значениям А>1 (усиление амплитуды), а нижняя полуплоскость — значениям А 0, r>0, T>0, 0











