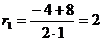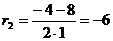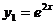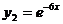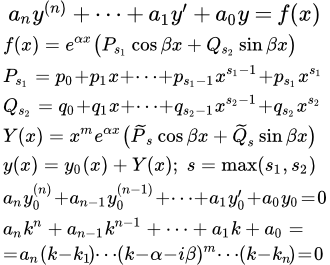Дифференциальные уравнения с синусом и косинусом как решать

y» +4y’ — 12y = 8sin(2x)

Решение уравнения будем искать в виде y = e rx находим с помощью калькулятора. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 +4 r — 12 = 0
D = 4 2 — 4 • 1 • (-12) = 64


Корни характеристического уравнения:
r₁ = 2
r₂ = -6
Следовательно, фундаментальную систему решений составляют функции:


Общее решение однородного уравнения имеет вид:

Рассмотрим правую часть:
f(x) = 8•sin(2•x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 0, Q(x) = 8, α = 0, β = 2.
Следовательно, число α + βi = 0 + 2i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида:
y * = Acos(2x) + Bsin(2x)
Вычисляем производные:
y’ = 2•B•cos(2x)-2•A•sin(2x)
y» = -4(A•cos(2x)+B•sin(2x))
которые подставляем в исходное дифференциальное уравнение:
y» + 4y’ -12y = (-4(A•cos(2x)+B•sin(2x))) + 4(2•B•cos(2x)-2•A•sin(2x)) -12(Acos(2x) + Bsin(2x)) = 8•sin(2•x)
или
-8•A•sin(2x)-16•A•cos(2x)-16•B•sin(2x)+8•B•cos(2x) = 8•sin(2•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
-8A -16B = 8
-16A + 8B = 0
Решая ее, методом Гаусса находим:
A = -1 /₅;B = -2 /₅;
Частное решение имеет вид:
y * = — 1 /₅cos(2x) — 2 /₅sin(2x)
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример 2.
4y’’ -8y’ + 5y = 5cos(x)
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
4 r 2 -8 r + 5 = 0
D = (-8) 2 — 4 • 4 • 5 = -16


Корни характеристического уравнения:
(комплексные корни):
r₁ = 1 + 1 /₂i
r₁ = 1 — 1 /₂i
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e x cos( 1 /₂x)
y₂ = e x sin( 1 /₂x)
Общее решение однородного уравнения имеет вид:

Рассмотрим правую часть:
f(x) = 5cos(x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 5, Q(x) = 0, α = 0, β = 1.
Следовательно, число α + βi = 0 + 1i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида:
y * = Acos(x) + Bsin(x)
Вычисляем производные:
y’ = Bcos(x)-Asin(x)
y» = -Acos(x)-Bsin(x)
которые подставляем в исходное дифференциальное уравнение:
4y» -8y’ + 5y = 4(-Acos(x)-Bsin(x)) -8(Bcos(x)-Asin(x)) + 5(Acos(x) + Bsin(x)) = 5cos(x)
или
8Asin(x)+Acos(x)+Bsin(x)-8Bcos(x) = 5cos(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
8A + B = 0
A -8B = 5
Решая ее методом Гаусса, находим:
A = 1 /₁₃;B = -8 /₁₃;
Частное решение имеет вид:
y * = 1 /₁₃cos(x) + -8 /₁₃sin(x)
Таким образом, общее решение дифференциального уравнения имеет вид:

Пример 3.
y»+3y’+2y=-24e -4x -20sin(2x)
Решаем в два этапа:
а) y»+3y’+2y=-24e -4x
б) y»+3y’+2y=-20sin(2x)
Затем объединяем полученные решения.

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Определение общего решения по известному частному решению

Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами n-го порядка:
(1) ,
где – действительные числа; – действительная функция. Если известно частное (любое) решение уравнения (1), то можно найти его общее решение по формуле:
,
где – общее решение однородного уравнения:
.

Если неоднородная часть может быть представлена в виде суммы функций:
,
то частное решение также может быть представлено в виде суммы частных решений:
,
каждое из которых удовлетворяет уравнению с правой частью в виде одной из функций :
.

Как правило, легче найти частные решения от более простых неоднородных частей, а затем получить частное решение для всего уравнения суммированием полученных частных решений.

Видео:2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Метод решения линейных ДУ с постоянными коэффициентами со специальной неоднородной частью

Рассмотрим линейное неоднородное уравнение со специальной неоднородной частью в виде комбинации многочленов, экспоненты, синусов и косинусов:
(2) ,
где – многочлены степеней и , соответственно:
;
;
– известные коэффициенты.

Это уравнение можно решить общим методом понижения порядка. Однако существует более простой способ, основанный на том, что частное решение такого уравнения имеет определенный вид. Суть этого метода заключается в следующем.

Вначале ищем общее решение однородного уравнения:
(3) .

Далее устанавливаем вид частного решения исходного уравнения (2). Оно выражается через многочлены, экспоненту, синусы и косинусы, которые входят в частное решение с неизвестными коэффициентами. Установив вид частного решения, подставляем в уравнение (2). Приравнивая левую и правую части, находим неизвестные коэффициенты.

После этого общее решение исходного уравнения (2) равно сумме общего решения однородного уравнения плюс частное решение неоднородного:
.

Видео:Дифференциальные уравнения. 11 класс.Скачать

Установление вида частного решения

Установим вид частного решения уравнения (2). Для этого вначале ищем решение однородного уравнения (3) в виде . В результате, для k , получаем уравнение, которое называется характеристическим уравнением:
(4) .
Решаем это уравнение. Получаем n корней . Тогда характеристическое уравнение (4) можно представить в виде произведения множителей:
(5) .

Часть корней (или все) в (5) могут быть комплексными. Поэтому выразим корень через действительную и мнимую части:
.
Для действительного корня .

Некоторые корни в (5) могут быть кратными:
.
Здесь p – кратность корня. Кратный корень кратности p входит в произведение (5) в виде множителя .

Если среди корней характеристического уравнения (4) нет корня со значением
,
то частное решение уравнения (2) имеет вид:
,
где – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами , которые подлежат определению подстановкой в уравнение (2).

Если среди корней характеристического уравнения (4) есть корень кратности p со значением

то частное решение уравнения (2) имеет вид:
,
где также – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами .

Когда вид частного решения установлен, подставляем Y в уравнение (2) и находим неизвестные коэффициенты , приравнивая левую и правую части уравнения. После чего получаем общее решение уравнения (2):
.

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Частные случаи

Неоднородность в виде многочлена

Теперь рассмотрим некоторые более простые виды специальной неоднородности. Начнем с неоднородной части в виде многочлена:
,
где – многочлен степени s . Этот случай принадлежит к общему виду специальной неоднородности (2), в котором . Основываясь на вышеизложенном, получаем следующие правила составления вида частного решения.

Если среди корней характеристического уравнения (4) нет нулевого корня
,
то частное решение имеет вид:
.
То есть оно является многочленом степени s с неопределенными коэффициентами .

Если характеристическое уравнение (4) имеет нулевой корень кратности p :
,
то частное решение имеет вид:
.

Неоднородность в виде произведения экспоненты и многочлена

Теперь рассмотрим неоднородную часть в виде произведения многочлена степени s и экспоненты:
.
Этот случай принадлежит к общему виду (2), в котором .

Если среди корней характеристического уравнения нет действительного корня со значением α :
,
то частное решение является произведением многочлена степени s и экспоненты:
.

Если характеристическое уравнение (4) имеет действительный корень α кратности p :
,
то частное решение имеет вид:
.

Неоднородность в виде суммы произведений многочленов на косинус и синус

Наконец рассмотрим неоднородную часть в виде суммы произведений многочленов степеней на косинус и синус:
.
Этот случай принадлежит к общему виду (2), в котором .

Если среди корней характеристического уравнения нет чисто мнимого корня со значением iβ :
,
то частное решение является суммой произведений многочленов, косинуса и синуса:
,
где – наибольшее из и .
,

– многочлены степени s с неизвестными коэффициентами .

Если характеристическое уравнение (4) имеет чисто мнимый корень iβ кратности p :
,
то частное решение имеет вид:
.
То есть частное решение как и в предыдущем случае, но умноженное на .

Автор: Олег Одинцов . Опубликовано: 30-07-2013 Изменено: 14-09-2020

💡 Видео

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

ЛНДУ II п. со спец. правой ч. (sin, cos)Скачать

Дифференциальные уравнения, 6 урок, Уравнения в полных дифференциалахСкачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

Решение задачи Коши дифференциального уравнения #maths #calculus #differentialequation #algebraСкачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Частное решение дифференциального уравнения. 11 класс.Скачать

Дифференциальные уравнения с разделяющими переменными. 11 класс.Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать