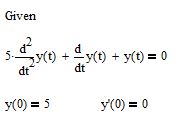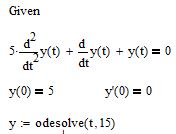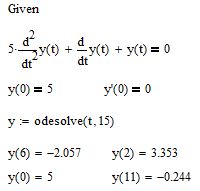Дифференциальные уравнения с параметром в mathcad (2 видео)

Дифференциальные уравнения с параметром в mathcad

Глава 5. Решение дифференциальных уравнений

5 .1 Вычислительный блок Given– Odesolve

Применение функции Odesolve требует записи вычислительного блока, состоящего из трех частей:

1) ключевого слова Given (Дано);

2) дифференциального уравнения и начальных или граничных условий к нему;

3) функции о desolve ( x , xk , n ) (решение ОДУ), где x – имя переменной, относительно которой решается уравнение; xk – конец интервала интегрирования (начало интервала интегрирования указано ранее, в начальных условиях); n – необязательный внутренний параметр, определяющий число шагов интегрирования, на которых решается дифференциальное уравнение.

Примеры использования функции Odesolve приведены на рис. 5.2–5.5.

Given

граничные условия можно задавать лишь в двух точках:

в начале и в конце интервала интегрирования

Рис. 5.2 Решение уравнения с граничными условиями

Если вид дифференциального уравнения изменяется с изменением аргумента, например, уравнение содержит ступенчатую разрывную функцию, то такое уравнение можно записать с использованием условия, то есть записать несколько уравнений в виде одного уравнения (рис. 5 . 3 ).

MathCAD позволяет записать условие несколькими способами:

– с использованием булевых операторов:

;

– с использованием функции if :

В данном случае невозможно записать условие с использование условного оператора программирования if , так как вертикальной черте (обязательному признаку программирования) должен предшествовать оператор присваивания :=, тогда как в нашем случае использован знак + или знак логического равенства =.

поменяйте местами закрашенные выражения

Given

Рис. 5.3 Объединение двух дифференциальных уравнений в одно

В MathCAD все встроенные функции для решения дифференциальных уравнений требуют записи производной высшего порядка в явном виде. Однако, как показано на рис. 5 . 2 , присутствие коэффициента (постоянного или переменного) перед производной высшего порядка – не помеха при решении ОДУ. Если уравнение есть сложная функция от высшей производной, предварительно надо решить это уравнение алгебраически относительно высшей производной. На рис. 5 .4. исходное уравнение решено символьно относительно у'(х). Для выполнения этой операции надо выделить переменную, затем в главном меню выбрать команду Symbolics → Variable → Solve (Символьные вычисления→Переменная→Решить). Найденный результат подставлен в дифференциальное уравнение, которое решено с помощью функции Odesolve.

В MathCAD 2001 i возможности функции Odesolve были расширены. Теперь она может решать и системы дифференциальных уравнений. При этом несколько изменяется обращение к ней.

Дано уравнение

решим его относительно у'(х)

has solution(s)

уравнение в стандартном виде подставим в блок Given — Odesolve

два корня уравнения дают решение ОДУ

Given

Рис. 5.4 Приведение дифференциального уравнения к стандртному виду и его решение

Обращение к функции для решения одного уравнения выглядит так:

о desolve ( x , xk , n ),

для решения системы дифференциальных уравнений–

о desolve ((вектор имен неизвестных), x , xk , n ).

Н а рис. 5 .5 приведено решение системы из трех дифференциальных уравнений первого порядка. соответственно, вектор имен неизвестных содержит имена трех неизвестных, х, у и z . Граничные условия заданы в точке t = –1. конечная точка интервала интегрирования t =3. Следовательно, интервал интегрирования от –1 до 3. Конечное значение всегда должно быть больше начального.

Если график строится для значений, выходящих за пределы интервала интегрирования, MathCAD экстраполирует значения функции за пределы интервала интегрирования, получая чаще всего неправдоподобные результаты.

Если в MathCAD 11 функция Odesolve решает системы уравнений только с начальными параметрами, то в MathCAD 12, 13, 14 – и с начальными, и с граничными условиями.

поменяйте вид уравнений и граничные условия

Рис. 5.5 Решение системы ОДУ функцией Odesolve

В MathCAD 2001 i у функции Odesolve появилась возможность принимать в качестве ограничений алгебраические уравнения (рис. 5.6 и 5.7), но только в задачах с начальными условиями.

Рассмотрим механизм работы блока Odesolve: блок Odesolve преобразует заданные дифференциальные уравнения к стандартному виду, используемому функциями rkfixed и Rkadapt . С помощью указанных функций он решает систему ОДУ (или одно ОДУ) с начальными условиями. В результате расчета получают массив значений функции и ее производные.

Далее используются функции интерполяции lspline и interp , преобразующие массив решений системы ОДУ в функцию, которую затем можно дифференцировать или интегрировать. Необязательный параметр steps в обращении к функции Odesolve как раз и задает число точек интерполяции. Чем больше steps , тем выше точность интерполяции, но тем больше время решения задачи.

При решении системы ОДУ есть возможность выбрать метод решения. Для этого надо установить курсор на слове Odesolve и нажать правую кнопку мыши. В открывшемся контекстном меню выбрать Fixed (Решение с фиксированным шагом функцией rkfixed ), Adaptive (Решение с переменным шагом функцией Rkadapt ) или Stiff (Решение жесткой системы ОДУ функцией Radau ) , как показано на рис. 5.7 .

дифференциальные

уравнения

алгебраическое уравнение

требуется 6 начальных условий:

Рис. 5. 6 Решение системы ОДУ с алгебраическими ограничениями функцией Odesolve

Given

Рис. 5.7 В ыбор метода решения дифференциальных уравнений

Содержание

Решение дифференциальных уравнений в MathCad 15
Функция odesolve
Тема 7. Решение дифференциальных уравнений и систем в MathCad
🎦 Видео

Видео:1 Одно уравнениеСкачать

Решение дифференциальных уравнений в MathCad 15

В статье рассмотрена работа функции odesolve для графического решения дифференциального уравнения в программе mathcad версии 15 и старше

Видео:Mathcad-10. Пример: дифференциальные уравненияСкачать

Функция odesolve

Для примера рассмотрим простейшее дифференциальное уравнение, описывающее затухающие колебания маятника с течением времени

В свободном поле mathcad введите оператор Given. Этот оператор запускает процесс ввода исходных данных для корректной работы функции odesolve. После этого найдите панель под названием Calculus. В этой панели нам понадобятся кнопки Derivative и Nth Derivative. Эти кнопки вводят заготовки для дифференциального уравнения. С помощью клавиатуры введите уравнение, как показано на рисунке 1. Знак равенства необходимо использовать из панели Boolean

Рис. 1. Ввод исходных данных для решения дифференциального уравнения

Далее введите начальные приближения. Количество начальных приближений зависит от порядка дифференциального уравнения. В нашем случае их будет 2. Введите приближения, как показано на рисунке 2. Обратите внимание, что для ввода значания первой производной вам нужно использовать символ «верхний апостроф«. Если вы его не можете ввести с клавиатуры вручную воспользуйтесь приложением windows Capter Map или используйте комбинацию клавиш Alt + 96 или Alt + 39

Рис. 2. Ввод первого приближения для решения дифференциального уравнения

Теперь, после начального приближения введите любую переменную (например y) и присвойте ей функцию Odesolve, как показано на рисунке 3. В качестве параметров функции Odesolve используется переменная t и интервал интегрирования. В нашем случае интервал равен 15

Рис. 3. Ввод функции odesolve для решения дифференциального уравнения

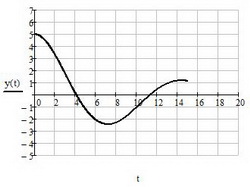
Можно отобразить функцию y на графике, где в качестве аргумента будет переменная t. Этот график и будет являться решением дифференциального уравнения. Обратите внимание, что график строится в пределах интервала интегрирования. Особенности оформления и отображения графиков в mathcad 15 смотрите в соответствующем разделе

Рис. 4. Вывод результата решения дифференциального уравнения на график

После корректного решения дифференциального уравнения функцию y(t) можно использовать далее в расчетах

Рис. 5. Результат решения дифференциального уравнения в mathcad 15 и старше

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

Видео:Работа с MathCad Prime. Решение дифференциальных уравнений.Скачать

Тема 7. Решение дифференциальных уравнений и систем в MathCad

Краткие теоретические сведения

Для решения дифференциальных уравнений с начальными условиями система Mathcad имеет ряд встроенных функций:

rkfixed – функция для решения ОДУ и систем ОДУ методом Рунге–Кутта четвертого порядка с постоянным шагом;

Rkadapt – функция решения ОДУ и систем ОДУ методом Рунге–Кутта с переменным шагом;

Odesolve – функция, решающая ОДУ блочным методом.

Ниже приведено описание стандартной функции rkfixed с указанием параметров функции.

y – вектор начальных условий из k элементов ( k – количество уравнений в системе);

x1 и x2 – левая и правая границы интервала, на котором ищется решение ОДУ или системы ОДУ;

p – число точек внутри интервала (x1, x2), в которых ищется решение;

D – вектор, состоящий из k-элементов, который содержит первую производную искомой функции или первые производные искомых функций, если речь идет о решении системы.

Результатом работы функции является матрица из p +1 строк, первый столбец которой содержит точки, в которых получено решение, а остальные столбцы – сами решения.

На рисунке 2.7.1 приведены конкретные примеры решения различных дифференциальных уравнений и систем ОДУ в MathCAD .

Рисунок 2.7.1 – Примеры решения дифференциальных уравнений и систем

При решении дифференциального уравнения первого порядка нужно создать вектор начальных условий из одного элемента Y 1 , который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции rkfixed указывается имя вектора Y , границы интервала, на котором ищется решение уравнения, например, (0 ; 2), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D . В результате получается матрица z , в первом столбце которой содержатся значения аргумента искомой функции, во втором – значения самой результирующей функции. При построении графика функции первый столбец полученной матрицы указывается как аргумент, второй столбец – как функция.

При решении системы дифференциальных уравнений нужно создать вектор начальных условий из двух элементов, например, вектор v , который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции rkfixed указывается имя вектора v , и границы интервала, на котором ищется решение уравнения, например, (0 ; 5), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D . В результате получается матрица s , в первом столбце которой содержатся значения аргумента искомых функций, во втором и третьем столбцах – значения самих функций при соответствующем значении аргумента. При построении графика можно воспользоваться первым столбцом полученной матрицы как аргументом, а вторым и третьим столбцами – как функциями.

На рисунке 2.7.2 приведен пример решения дифференциального уравнения второго порядка с использованием функции rkfixed . Необходимо решить дифференциальное уравнение второго порядка с заданными начальными условиями вида:

Рисунок 2.7.2 – Пример решения дифференциальных уравнений второго порядка с помощью rkfixed

Для решения уравнения с помощью функции rkfixed нужно выполнить замену переменных и привести дифференциальное уравнение второго порядка к двум дифференциальным уравнениям первого порядка. Вид этих уравнений приведен ниже.

Документ формируется точно так же, как и при решении системы ОДУ.

На рисунке 2.7.2 показана возможность вычисления вектора второй производной найденной функции – вектора а, построены графики исходной функции, функций первой и второй производных.

Практическая часть темы 7

7.1 Решение дифференциальных уравнений первого порядка

Последовательность действий для р ешения дифференциального уравнения первого порядка такова:

q сформировать вектор начальных условий из одного элемента, присвоив начальное значение искомой функции переменной с индексом, например: или (в зависимости от значения переменной ORIGIN );

q определить вектор-функцию из одного элемента, которая содержит первую производную неизвестной функции:

· набрать имя функции с двумя параметрами: первый параметр – аргумент искомой функции (независимая переменная), второй – имя вектора, содержащего искомую функцию (можно использовать имя вектора начальных условий), например, D ( x , Y );

· набрать оператор «:=» и выражение для первой производной (выразить из дифференциального уравнения), в котором вместо имени искомой функции подставлен первый элемент вектора-параметра, например, для уравнения вектор-функция будет определятся следующим образом: ( если ORIGIN = 0 , подставлять );

q присвоить некоторой переменной значение функции rkfixed , указав в скобках следующие параметры:

· первый – имя вектора начальных условий,

· второй – левая граница интервала, на котором ищется решение, в виде числовой константы,

· третий – правая граница интервала, на котором ищется решение, в виде числовой константы,

· четвертый – количество точек, в которых ищется решение,

· пятый – имя вектора-функции, описывающего первую производную, без параметров;

например: ,

(в результате получится матрица Z , в первом столбце которой содержатся значения аргумента искомой функции, во втором – значения самой функции);

q вывести матрицу, содержащую решение ДУ с помощь оператора «=», например: Z = ;

q построить график найденной функции ( см. тему 5 ), указав в качестве аргумента по оси абсцисс столбец , а в качестве значения функции по оси ординат – столбец ( если ORIGIN = 0 , набирать соответственно и ).

Пример 7.1 Найти численное решение дифференциального уравнения первого порядка на интервале от 0.2 до 5 в 1000 точках, при начальном условии y (0)=0.1.

Выполнить графическую интерпретацию результатов.

7.2 Решение систем дифференциальных уравнений

Последовательность действий для р ешения системы дифференциальных уравнений первого порядка такова (описана для значения ORIGIN =0 ):

q перейти в исходной системе уравнений к однотипным обозначениям функций и выразить первые производные,

например, систему можно преобразовать в ;

q в документе MathCad сформировать вектор начальных условий, количество элементов которого равно количеству уравнений системы, присвоив его некоторой переменной (см. тему 2);

например, ;

q определить вектор-функцию, которая содержит первые производные искомых функций:

· набрать имя функции с двумя параметрами: первый параметр – аргумент искомых функций (независимая переменная), второй – имя вектора, содержащего искомые функции (можно использовать имя вектора начальных условий), например, D ( t , V );

(Замечание: если независимая переменная явно не присутствует в системе, то в качестве ее имени можно выбрать любую переменную)

· набрать оператор «:=» и вставить шаблон вектора, количество элементов которого равно количеству уравнений системы (см. тему 2)

· набрать в качестве элементов вектора правые части системы уравнений, в которых искомые функции представлены соответствующими элементами вектора-параметра, например,

;

q присвоить некоторой переменной значение функции rkfixed , указав в скобках следующие параметры:

· первый – имя вектора начальных условий,

· второй – левая граница интервала, на котором ищется решение, в виде числовой константы,

· третий – правая граница интервала, на котором ищется решение, в виде числовой константы,

· четвертый – количество точек, в которых ищется решение,

· пятый – имя вектора-функции, описывающего первые производные, без параметров;

например: ,

(в результате получится матрица Z , в первом столбце которой содержатся значения аргумента искомых функций, во втором – значения первой функции, в третьем – значения второй функции и т. д.);

q вывести матрицу, содержащую решение системы ДУ с помощь оператора «=», например: Z = ;

q построить графики найденных функций ( см. тему 5 ), указав в качестве аргумента по оси абсцисс первый столбец матрицы решений, например, , а в качестве значений функций по оси ординат – остальные столбцы матрицы через запятую, например, , и т. д.