Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать
Дифференциальные уравнения равновесия Эйлера
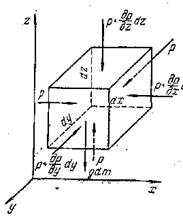
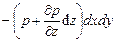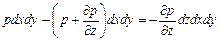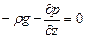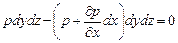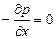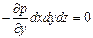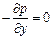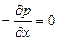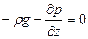В объеме жидкости, находящейся в покое, выделим элементарный параллелепипед объемом dV с ребрами dx, dy и dz, расположенными параллельно осям координат х, у и z (рис. II-2). Сила тяжести, действующая на параллелепипед, выражается произведением его массы dm на ускорение свободного падения g, т.е. равна gdm. Сила гидростатического давления на любую из граней параллелепипеда равна произведению гидростатического давления р на площадь этой грани. Будем считать, что давление р является функцией всех трех координат; р = f (x, у, z). Выяснение вида этой функции, т.е. закона распределения гидростатического давления по объему жидкости, и является нашей задачей.
Согласно основному принципу статики, сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна нулю. В противном случае происходило бы перемещение жидкости.
Рассмотрим сумму проекций сил на ось z. Сила тяжести направлена вниз, параллельно оси z. Поэтому при выбранном положительном направлении оси z (см. рис. II-2) сила тяжести будет проектироваться на эту ось со знаком минус:
-gdm = -grdV = — rgdxdydz
Рис. II-2. К выводу дифференциальных уравнений равновесия Эйлера.
Сила гидростатического давления действует на нижнюю грань параллелепипеда по нормали к ней, и ее проекция на ось z равна p dx dy. Если изменение гидростатического давления в данной точке в направлении оси z равно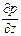 
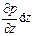
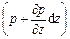
, то по всей длине ребра dz оно составит 
. Тогда гидростатическое давление на противоположную (верхнюю) грань равно 
и проекция силы гидростатического давления на ось z
Проекция равнодействующей силы давления на ось z
Сумма проекций сил на ось z равна нулю, т.е.
(II,14)
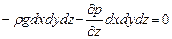
или, учитывая, что объем параллелепипеда dxdydz = dV ¹ 0 (величина, заведомо не равная нулю), получим
Проекции сил тяжести на оси х и у равны нулю. Поэтому сумма проекций сил на ось х
откуда после раскрытия скобок и сокращения находим
(II,14a)
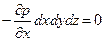
Соответственно для оси у
Таким образом, условия равновесия элементарного параллелепипеда выражаются системой уравнений:
(II,15)
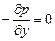
Уравнения (II, 15) представляют собой дифференциальные уравнения равновесия Эйлера.
Для получения закона распределения давления во всем объеме покоящейся жидкости следует проинтегрировать систему уравнений (II, 15), Интегралом этих уравнений является основное уравнение гидростатики, широко используемое в инженерной практике.
Дата добавления: 2016-02-16 ; просмотров: 1798 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Теорема Эйлера о движении жидкостиСкачать
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ ЖИДКОСТИ. УРАВНЕНИЯ ЭЙЛЕРА
Рассмотрим некоторый объем покоящейся жидкости (рис. 1.4). Выделим в ней вокруг рассматриваемой точки А бесконечно малый параллелепипед с ребрами dx, dy, dz. Отбросим мысленно окружающую его жидкость, а ее воздействие на грани заменим силами, действующими со стороны жидкости, — Рх и Р’х, Ру и F, Рг и Р Кроме того, в точке А как в центре массы выделенного элемента приложим равнодействующую массовых сил Q.
Рис. 1.4. Схема к выводу уравнения Эйлера
Запишем условие равновесия на осьх:
Давление рх и р’х можно выразить через давления в точке А:
Тогда уравнение равновесия перепишется
Отсюда +рХ = 0, или — = рХ.
Аналогичные уравнения можно получить, рассматривая проекцию на другие оси.
В результате будем иметь
Это и есть общие уравнения равновесия жидкости, полученные Эйлером.
Видео:Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать
ВЫВОД ФОРМУЛЫ ПРИРАЩЕНИЯ ДАВЛЕНИЯ И ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПОВЕРХНОСТИ РАВНЫХ ДАВЛЕНИЙ
Основной задачей гидростатики является получение:
• зависимости гидростатического давления в точке от ее координат
• уравнения поверхности равных давлений
Для получения уравнения изменения давления при смещении от данной точки А на бесконечно малое расстояние dl, проекции которого на оси координат соответственно будут dx, dy, dz, преобразуем уравнения Эйлера. Умножим соответственно каждое уравнение на приращения координатах, dy, dzn, суммировав левые и правые части, получим
Но левая часть этого уравнения есть полный дифференциал dp, выражающий изменение давления р при смещении точки на бесконечно малое расстояние, тогда имеем
То есть получили дифференциальное уравнение изменения давления в функции координат точки. Решение этого уравнения в виде (1.13) может быть выполнено путем интегрирования для данной конкретной задачи.
Перейдем к рассмотрению уравнения поверхности равного давления, определяемого условием р = const.
Из условия постоянства давления следует dp = 0. Подставляя это выражение в (1.15) и учитывая, что р ф 0, получим
Уравнение (1.16) связывает координаты точек равных давлений, т.е. оно является дифференциальным уравнением поверхности равных давлений.
Решение этого уравнения в виде (1.14) должно также проводиться путем интегрирования для конкретных задач. К рассмотрению одной из таких задач и перейдем.
Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать
Дифференциальные уравнения Эйлера для однофазного потока идеальной жидкости (газа) в статике
В объеме жидкости, находящейся в покое, выделим элементарный параллелепипед dV с ребрами dx,dy,dz (рис.6.3.). Сила тяжести, действующая на параллелепипед, выражается произведением его массы dm на ускорение свободного падения g.
Сила гидростатического давления на любую из граней параллелепипеда равна произведению давления р на площадь этой грани. Будем считать, что давление р является функцией всех трех координат p=f(x,y,z). Выяснение вида этой функции (т.е. закона распределения гидростатического давления по объему жидкости) и является нашей задачей [3,4, 6].
Как известно, в статике сумма проекций всех сил на оси координат, действующих на элементарный объем, равна нулю. В противном случае происходило бы перемещение жидкости.
Рассмотрим сумму проекций сил на ось z. Сила тяжести направлена вниз, параллельно оси z, поэтому она будет проектироваться на эту ось со знаком минус:
Сила гидростатического давления р действует на нижнюю грань параллелепипеда по нормали к ней, и её проекция на ось z равна pdxdy. Если изменение гидростатического давления в данной точке в направлении оси
z равно ^, то по всей длине ребра dz это изменение составит — dz.
Рис.6.3. К выводу дифференциальных уравнений Эйлера в статике
Тогда гидростатическое давление на противоположную (верхнюю) грань равно + а проекция силы гидростатического давления на ось z
равна 
Проекция равнодействующей силы давления на ось z составит:
Сумма проекций сил тяжести и гидростатического давления на ось z равна нулю:
Так как проекции сил тяжести на оси х и у равны нулю, поэтому сумма проекций сил на ось х и у:
откуда находим или
Таким образом, для элементарного параллепипеда условие равновесия (в статике) имеет вид:
где р — гидростатическое давление на грани; р — плотность жидкости; g — ускорение свободного падения
Это дифференциальное уравнение Эйлера при равновесии (статике) жидкости.
Для получения закона распределения давления по всему объему покоящейся жидкости следует проинтегрировать это уравнение, которое является основным уравнением гидростатики, широко используемым в инженерной практике.
Из последнего уравнения следует, что давление находящейся в статике жидкости изменяется только по вертикали (вдоль оси z рис.6.3). В
связи с тем, что частные производные — и — равны нулю, частная про-
изводная — может быть заменена на полную производную — и, следо- dz dz
Для несжимаемой однородной жидкости плотность (р) постоянна, тогда последнее уравнение можно представить в следующем виде:
отсюда после интегрирования получим:
Это основное уравнение гидростатики. Первый член уравнения — геометрический напор, второй член — статический (или пьезометрический) напор, характеризующий потенциальную энергию жидкости, приходящуюся на единицу веса жидкости. Из уравнения следует, что сумма статического и геометрического напоров для поверхностей любого уровня постоянна и выражает полный гидростатический напор (в м).
Для двух произвольно выбранных горизонтальных плоскостей 1 и 2 это уравнение имеет в вид:
где z,z-i — высоты расположения двух точек внутри покоящейся однородной капельной жидкости над произвольно выбранной горизонтальной плоскостью отсчета; р.рг — гидростатические давления в этих точках.
Из основного уравнения гидростатики можно получить известное уравнение Паскаля:
Это уравнение позволяет рассчитать давление в любой точке объема жидкости и является выражением общего закона гидростатики, который формулируется следующим образом: давление в любой точке покоящейся жидкости (в данной горизонтальной плоскости) складывается из внешнего давления ро и давления столба жидкости pgh. Давление столба жидкости pgh высотой h (от поверхности до данной точки) и площадью основания, равной единице.
Закон гидростатики в такой формулировке справедлив для всех жидкостей, газов и их смесей.
Уравнение Паскаля широко используют при расчете различных гидростатических приборов и машин.
📺 Видео
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
Урок 133. Закон Бернулли. Уравнение БернуллиСкачать
Линейное дифференциальное уравнение Коши-ЭйлераСкачать
Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать
7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
#Дифуры II. Урок 5. Уравнение ЭйлераСкачать
Дифференциальные уравнения. 11 класс.Скачать
14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать
2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать
Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать
дифференциальное уравнение ЭйлераСкачать
Дифференциальное уравнение. Формула ЭйлераСкачать
18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать
1. Что такое дифференциальное уравнение?Скачать
