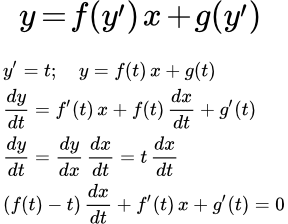Дифференциальные уравнения лагранжа и метод его решения (2 видео)

Содержание

Дифференциальное уравнение Лагранжа
Решение дифференциального уравнения Лагранжа
Дополнительные решения дифференциального уравнения Лагранжа
Пример
Уравнение Лагранжа
Общий метод решения уравнения Лагранжа
Решение типичных задач
Готовые работы на аналогичную тему
ЛДУ с переменными коэффициентами. Метод Лагранжа
Линейные дифференциальные уравнения с переменные коэффициентами
Составление дифференциального уравнения по заданной фундаментальной системе решений
Разные задачи
🎥 Видео

Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Дифференциальное уравнение Лагранжа

Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Решение дифференциального уравнения Лагранжа

Рассмотрим дифференциальное уравнение Лагранжа:
(1) ,
где и – это функции.
Будем искать его решение в параметрическом виде. То есть будем считать, что , , а также производная являются функциями от параметра . Положим
.
Поставим в (1):
(2) .
Продифференцируем по :
(3) .
С другой стороны:
(4) .
Левые части уравнений (3) и (4) равны. Приравниваем правые части и выполняем преобразования:
;
.

Разделим на . При уравнение принимает вид:
.
Это линейное дифференциальное уравнение относительно переменной . Решая его, получаем зависимость переменной от параметра : . Затем подставляем в (2):
.
В результате получаем зависимость переменной от параметра : . То есть мы получили параметрическое представление решения уравнения (1).

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дополнительные решения дифференциального уравнения Лагранжа

В процессе приведения уравнения к линейному, мы разделили уравнение на . Поэтому мы рассматривали решение при . В заключении следует рассмотреть случай , то есть исключить параметр из уравнений:
(5) ;
(6) .

Уравнение (5) содержит только переменную t . Поэтому его нужно решить и определить корни. Если корней нет, то дополнительных решений также нет.

Предположим, что мы нашли корни уравнения (5) (один или несколько). Обозначим такой корень как :
(7) .
Тогда уравнение (6) дает нам зависимость y от x , которая является линейной функцией:
.
Поскольку в силу (7), , то
(8) .

Покажем, что (8) является решением исходного уравнения (1). Для этого найдем производную (8). Она равна постоянной:
.
Подставим (8) и в (1):
;
;
.
Это уравнение выполняется, поскольку в силу (7), .

Таким образом, мы нашли, что уравнение (1) может иметь решения
,
где – корни уравнения
.

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Пример

Решить уравнение:
(1.1)

Разделим на . При имеем:
(1.2) .
Это уравнение Лагранжа. Ищем решение в параметрическом виде. Считаем, что , , а также — это функции от параметра . Положим . Тогда
(1.3) .

Чтобы упростить выкладки, умножим (1.3) на знаменатель дроби и продифференцируем по :
;
;
(1.4) .
Далее имеем:
(1.5) .
Поставляем (1.3) и (1.5) в (1.4) и выполняем преобразования:
;
;
.
Разделим на . При ( или при и при ) имеем:
.

Разделяем переменные и интегрируем:
;
;
.
Потенцируем:
.
Заменим постоянную . Знак модуля сводится к умножению на постоянную ±1, которую включаем в .
.
Отсюда
;
.
Подставляем в (1.3):
.
Заменим постоянную :
.

Теперь рассмотрим значения , которые мы исключили из рассмотрения при выполнении операций деления. Для этого подставим эти значения в исходное уравнение (1.1),
(1.1) .
Проверим, существует ли для этих значений дополнительные решения.

1) Подставим в (1.1):
.
Отсюда . Решение удовлетворяет исходному уравнению (1.1).

2) Подставим в (1.1):
;
.
Значение не удовлетворяет исходному уравнению. Отбрасываем его.

3) Подставим в (1.1):
;
;
.
Решение удовлетворяет исходному уравнению.

Общее решение уравнения имеет вид:
;
;
.

Автор: Олег Одинцов . Опубликовано: 26-08-2012 Изменено: 24-11-2021

Видео:19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Уравнение Лагранжа

Вы будете перенаправлены на Автор24

Видео:10. Уравнения БернуллиСкачать

Общий метод решения уравнения Лагранжа

Предположим, что некоторое дифференциальное уравнение первого порядка $Fleft(x,y,y’right)=0$, не разрешенное относительно производной, удалось разрешить относительно $y$, то есть представить в виде $y=fleft(x,y’right)$.

Частным случаем дифференциального уравнения такого вида является уравнение Лагранжа $y=xcdot phi left(y’right)+psi left(y’right)$, в котором $phi left(y’right)ne y’$.

Дифференциальное уравнение Лагранжа решают методом введения параметра $y’=p$.

При этом исходное дифференциальное уравнение можно переписать в виде $y=xcdot phi left(pright)+psi left(pright)$.

Выполнив дифференцирование по $x$ с учетом $dy=pcdot dx$, после несложных алгебраических преобразований получаем линейное дифференциальное уравнение относительно функции $xleft(pright)$ и её производной $frac $, а именно: $frac -frac cdot x=frac $.

Это уравнение решается известным методом, в результате чего получим его общее решение $x=Fleft(p,Cright)$.

Подставив полученный результат в соотношение $y=xcdot phi left(pright)+psi left(pright)$, получим $y=Fleft(p,Cright)cdot phi left(pright)+psi left(pright)$.

Дополнительные частные либо особые решения уравнения Лагранжа могут быть получены в результате нахождения действительных корней уравнения $p-phi left(pright)=0$ и подстановки их в $y=xcdot phi left(pright)+psi left(pright)$.

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Решение типичных задач

Решить дифференциальное уравнение $y=-xcdot y’+y’^ $.

Имеем дифференциальное уравнение Лагранжа, в котором $phi left(y’right)=-y’$ и $psi left(y’right)=y’^ $.

Вводим параметр $y’=p$ и получаем $y=-xcdot p+p^ $, а также $phi left(pright)=-p$ и $psi left(pright)=p^ $.

Теперь получим уравнение вида $frac -frac cdot x=frac $. Для этого находим: $phi ‘left(pright)=-1$; $psi ‘left(pright)=2cdot p$; $p-phi left(pright)=p-left(-pright)=2cdot p$.

Уравнение приобретает вид: $frac +frac cdot x=1$.

Применяем алгоритм решения линейного неоднородного дифференциального уравнения:

Стандартный вид $frac+fraccdot x=1$, где $Pleft(pright)=frac$, $Qleft(pright)=1$.
Вычисляем интеграл $I_ =int Pleft(pright)cdot dp =int fraccdot dp =fraccdot ln left|pright|$.

Выбираем для $vleft(pright)$ простейший ненулевой вариант: $vleft(pright)=frac <sqrt

> $.

Вычисляем интеграл $I_ =int fraccdot dp =int sqrt

cdot dp =fraccdot p^<frac> $ и получаем $uleft(p,Cright)=fraccdot p^<frac> +C$.

Получаем общее решение данного линейного неоднородного дифференциального уравнения в виде $x=left(fraccdot p^<frac> +Cright)cdot frac<sqrt

> =fraccdot p+frac<sqrt

> $.

Подставляем полученный результат в $y=xcdot phi left(pright)+psi left(pright)$. Получаем: $y=-left(frac cdot p+frac <sqrt

> right)cdot p+p^ =frac cdot p^ -Ccdot sqrt

Таким образом, общее решение данного уравнения Лагранжа в параметрической форме имеет вид: $left<begin <x=frac cdot p+frac <sqrt

> > \ <y=frac cdot p^ -Ccdot sqrt

> endright. $.

Для определения дополнительных частных либо особых решений находим корни уравнения $p-phi left(pright)=0$: получаем $p=0$.

Подставляем $p=0$ в $y=-xcdot p+p^ $ и получаем $y=0$. Это решение является частным, так как получается из общего при $C=frac cdot p^<frac > $.

Готовые работы на аналогичную тему

Решить дифференциальное уравнение $y=xcdot y’cdot left(y’+2right)$.

Имеем дифференциальное уравнение Лагранжа, в котором $phi left(y’right)=y’cdot left(y’+2right)$ и $psi left(y’right)=0$.

Вводим параметр $y’=p$ и получаем $y=xcdot pcdot left(p+2right)$, а также $phi left(pright)=pcdot left(p+2right)$ и $psi left(pright)=0$.

Теперь получим уравнение вида $frac -frac cdot x=frac $. Для этого находим: $phi ‘left(pright)=2cdot p+2$; $psi ‘left(pright)=0$; $p-phi left(pright)=p-left(p^ +2cdot pright)=-p^ -p$.

Уравнение приобретает вид:

Имеем стандартный вид $x’+Pleft(pright)cdot x=0$, где $Pleft(pright)=frac
$.
Вычисляем интеграл $I=int Pleft(pright)cdot dp =int frac
cdot dp =2cdot ln left|pright|$.
Записываем общее решение в виде $x=Ccdot e^ $ и выполняем упрощающие преобразования:

Подставляем полученный результат в $y=xcdot pcdot left(p+2right)$. Получаем: $y=frac <p^> cdot pcdot left(p+2right)$ или $y=Ccdot left(1+frac

right)$.

Таким образом, общее решение данного уравнения Лагранжа в параметрической форме имеет вид: $left<begin <x=frac <p^> > \ <y=Ccdot left(1+frac

right)> endright. $.

Параметр $p$ из этой системы можно исключить:

$p=frac <sqrt> <pm sqrt> $; $y=Ccdot left(1pm frac <2cdot sqrt> <sqrt> right)$ — это результат решения в явной форме.

Для определения дополнительных частных либо особых решений находим корни уравнения $p-phi left(pright)=-p^ -p=0$.

Получаем: $pcdot left(p+1right)=0$, откуда имеем два корня $p=0$ и $p=-1$.

Подставляем первый корень $p=0$ в $y=xcdot pcdot left(p+2right)$ и получаем первое дополнительное решение данного уравнения $y=0$. Это решение является частным, так как получается из общего при $C=0$.

Подставляем второй корень $p=-1$ в $y=xcdot pcdot left(p+2right)$ и получаем второе дополнительное решение данного уравнения $y=-x$. Это решение является особым, так как не получается из общего ни при каком $C$.

Видео:Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

ЛДУ с переменными коэффициентами. Метод Лагранжа

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Линейные дифференциальные уравнения с переменные коэффициентами

Если известно частное решение уравнения

то его порядок можно понизить на единицу (не нарушая линейности уравнения), полагая , где — новая неизвестная функция, а затем делая замену (можно непосредственно делать замену ).

Если известно частных линейно независимых решений уравнения (32), то порядок уравнения может быть понижен на единиц.

Общее решение уравнения

есть сумма какого-нибудь его частного решения и общего решения соответствующего однородного уравнения (32).

Если известна фундаментальная система соответствующего однородного уравнения (32), то общее решение неоднородного уравнения (33) может быть найдено методом вариации постоянных ( метод Лагранжа ).

Общее решение уравнения (32) имеет вид

где — произвольные постоянные.

Будем искать решение уравнения (33) в виде

где — некоторые пока неизвестные функции от . Для их определения получаем систему

Разрешая эту систему относительно , получаем

где — произвольные постоянные. Внося найденные значения в (34), получаем общее решения уравнения (33).

В частности, для уравнения второго порядка

Решая (36) относительно и , получаем

где и — постоянные интегрирования.

Замечание. Для уравнения , где , система (36) будет выглядеть так:

Пример 1. Найти общее решение уравнения , если есть его частное решение.

Решение. Положим , где — новая неизвестная функция от , тогда

Подставляя в данное уравнение, получаем

Но так как есть частное решение данного уравнения, то , поэтому имеем

Но , а значит , и уравнение (37) примет вид

Перепишем его в виде . Отсюда имеем , откуда

Интегрируя это уравнение, найдем и, следовательно, общее решение данного уравнения будет

Пример 2. Найти общее решение уравнения .

Решение. Общее решение соответствующего однородного уравнения имеет вид (см. пример 1)

и следовательно, его фундаментальная система решений будет

Будем искать общее решение данного уравнения методом вариации произвольных постоянных:

где — постоянные неизвестные функции от , подлежащие определению. Для их нахождения составим следующую систему:

Отсюда находим: . Интегрируя, получаем

Подставляя эти значения и в выражение для , найдем общее решение данного уравнения

Пример 3. Решить уравнение .

Решение. Соответствующее однородное уравнение будет . Его характеристическое уравнение имеет мнимые корни , и общее решение однородного уравнения имеет вид

Общее решение исходного уравнения ищем в виде

где и — неизвестные функции от . Для их нахождения составим систему

Разрешаем эту систему относительно и :

Подставляя выражения и в (38), получаем общее решение данного уравнения

Здесь есть частное решение исходного неоднородного уравнения.

Пример 4. Зная фундаментальную систему решений соответствующего однородного уравнения, найти частное решение уравнения

Решение. Применяя метод вариации постоянных, находим общее решение уравнения (39):

При первые два слагаемых правой части (40) стремятся к бесконечности, причем при любых , неравных нулю одновременно, функция есть бесконечно большая функция при . Третье слагаемое правой части (40) имеет пределом ноль при , что легко установить с помощью правила Лопиталя. Таким образом, функция , которая получается из (40) при и , будет решением уравнения (39), удовлетворяющим условию .

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Составление дифференциального уравнения по заданной фундаментальной системе решений

Рассмотрим линейно независимую на отрезке систему функций

имеющих все производные до n-го порядка включительно. Тогда уравнение

где — неизвестная функция, будет линейным дифференциальным уравнением, для которого, как нетрудно видеть, функции составляют фундаментальную систему решений. Коэффициент при в (42) есть определитель Вронского системы (41). Те точки, в которых этот определитель обращается в ноль, будут особыми точками построенного уравнения — в этих точках обращается в ноль коэффициент при старшей производной .

Пример 1. Составить дифференциальное уравнение, для которого образуют фундаментальную систему решений.

Решение. Применяя формулу (42), получаем

Раскрывая определитель в левой части (43) по элементам третьего столбца, будем иметь . Это и есть искомое дифференциальное уравнение.

Пример 2. Составить дифференциальное уравнение, для которого функции фундаментальную систему решений образуют функции .

Решение. Составим уравнение вида (42):

Раскрывая последний определитель по элементам 3-го столбца, будем иметь

В этом примере определитель Вронского обращается в ноль при . Это не противоречит общей теории, в силу которой определитель Вронского фундаментальной системы решений линейного однородного дифференциального уравнения

с непрерывными на отрезке коэффициентами не обращается в ноль ни в одной точке отрезка . Записав уравнение (44) в виде

видим, что коэффициент при терпит разрыв при , так что в точке непрерывность коэффициентов уравнения (45) нарушается.

Видео:Курс по ОДУ: Уравнения Клеро и Лагранжа | Занятие 8Скачать

Разные задачи

Пусть — фундаментальная система линейного однородного уравнения

Тогда имеет место формула Остроградского–Лиувилля

где — определитель Вронского, а — любое значение из отрезка , на котором непрерывны коэффициенты уравнения.

Пример 1. Показать, что линейное дифференциальное уравнение имеет решение вида , где — некоторый многочлен. Показать, что второе решение этого уравнения имеет вид , где — также многочлен.

Решение. Будем искать решение в виде многочлена, например, первой степени: . Подставляя в уравнение, найдем, что . Пусть , тогда ;. таким образом, многочлен будет решением данного уравнения. Перепишем данное уравнение в виде

Пусть — второе частное решение данного уравнения, линейно независимое с первым. Находим определитель Вронского системы решений

здесь . Применяя формулу Остроградского–Лиувилля, будем иметь

где — любое значение , причем , или ; здесь . Для нахождения получили линейное дифференциальное уравнение первого порядка. Деля обе части этого уравнения на , приведем его к виду