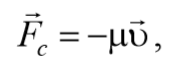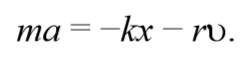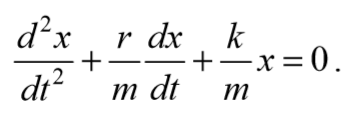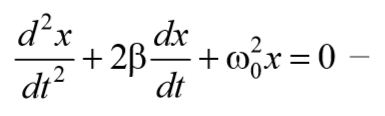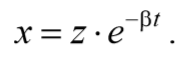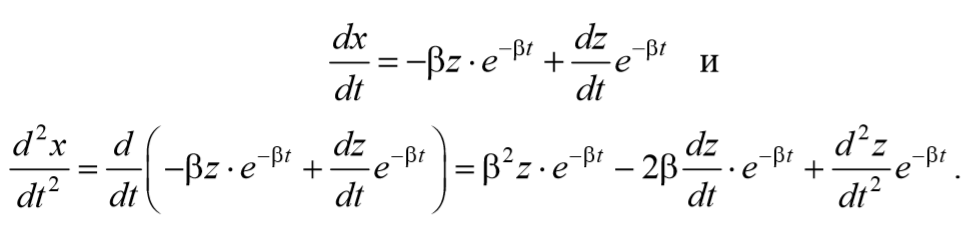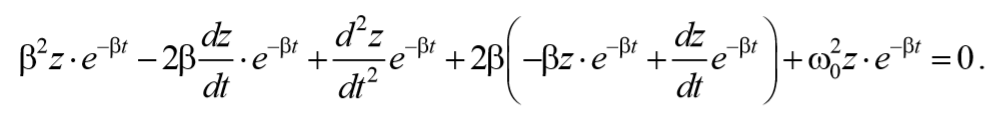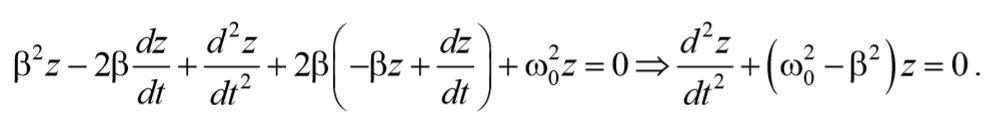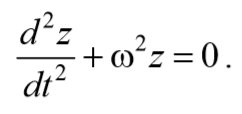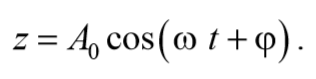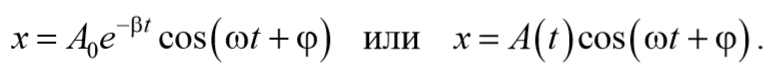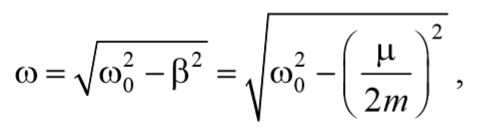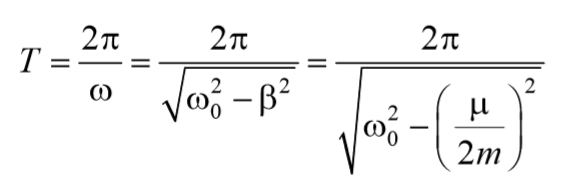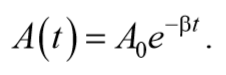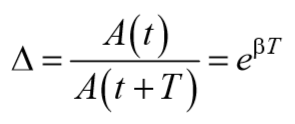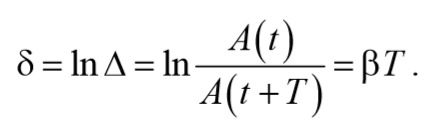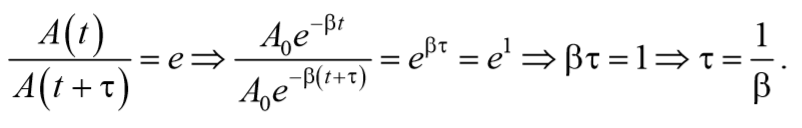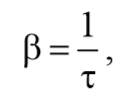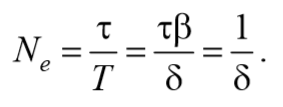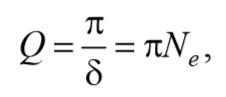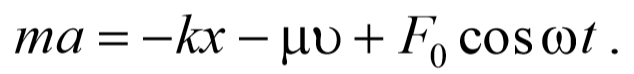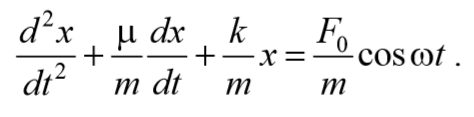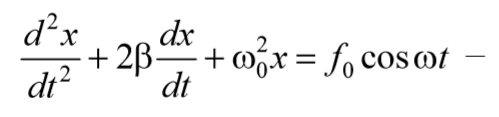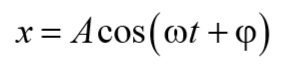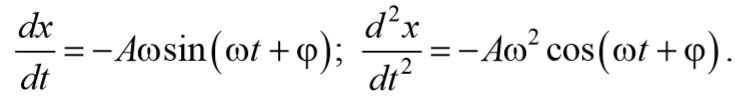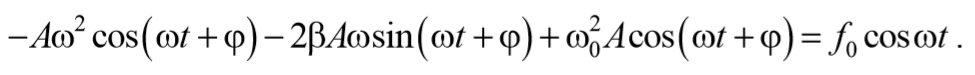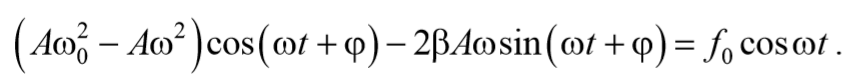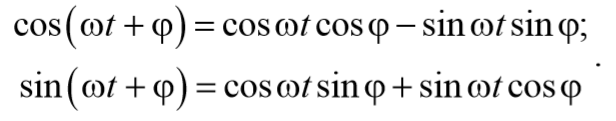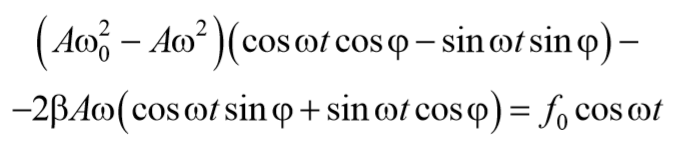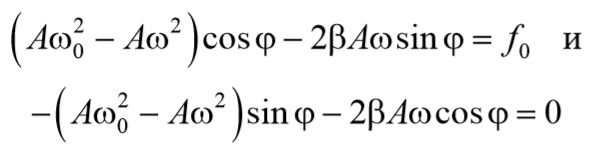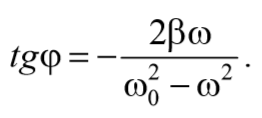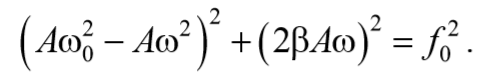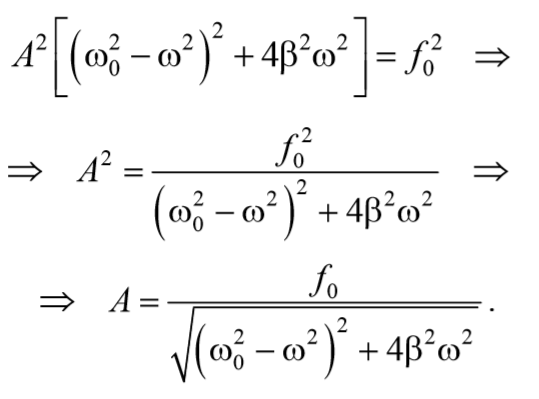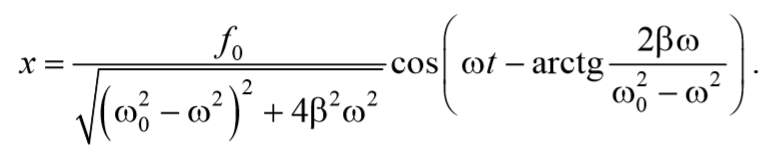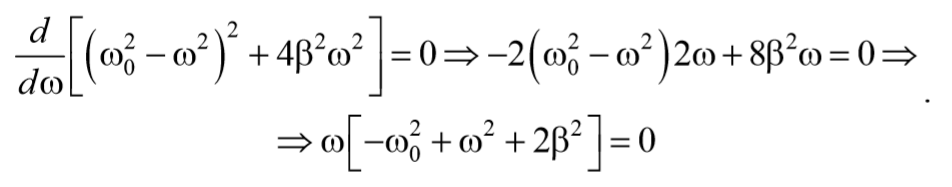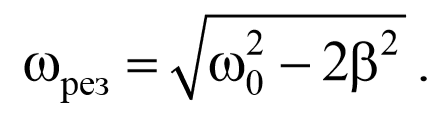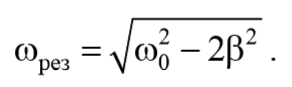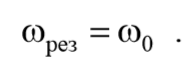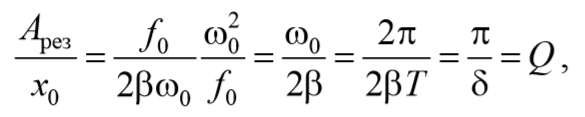Дифференциальные уравнения гармонических колебаний с затуханием и без затухания и их решения

Видео:5.4 Уравнение гармонических колебанийСкачать

Лекция №8. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

5.6. Затухающие гармонические колебания.

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. Затухающие колебания − это колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. В простейшем, и вместе с тем наиболее часто встречающемся случае, сила сопротивления, вызывающая затухание, зависит от скорости колебательного движения, т. е. ее можно считать прямо пропорциональной скорости

где μ − постоянная, называемая коэффициентом сопротивления.

Знак «минус» обусловлен тем, что сила и скорость имеют противоположные направления. Тогда второй закон Ньютона для гармонических колебаний при наличии сил сопротивления имеет вид

Учитывая , что a= $$d^2xover dt^2$$ , а υ= $$dxover dt$$ и разделив на массу m , получим

Применив обозначения $$ = ω_0$$ , $$ = 2β$$ и $$ = f_0$$ получим

дифференциальное уравнение затухающих колебаний . Отметим, что ω₀ представляет собой ту частоту, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды. Эта частота называется собственной частотой .

Для решения уравнения (5.6.4) сделаем подстановку

Проведем замену переменных

Подставим (5.6.5 и 5.6.6) в выражение (5.6.4)

Преобразуем , сократив на e -βt

Рассмотрим случай, когда сопротивление среды настолько мало, что ω₀ 2 -β 2 >0 есть величина положи мы можем ввести тельная, и обозначение ω₀ 2 -β 2 =ω 2 , после чего уравнение (5.6.8) примает вид

В случае большого сопротивления среды ω₀ 2 -β 2 , движение становится непериодическим.

Решение уравнения (5.6.8) можно записать в виде

Окончательно, подставляя последнее уравнение в выражение (5.6.5), получаем общее решение дифференциального уравнения затухающих колебаний (5.6.4)

В соответствии с видом полученной функции движение можно рассматривать как гармоническое колебание с частотой

и амплитудой, изменяющейся по закону

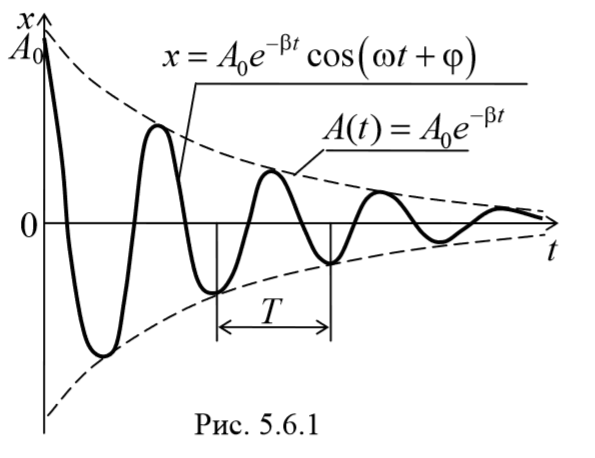
На рисунке показан график данной функции. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Верхняя из пунктирных кривых дает график функции A(t) , причем величина A₀ представляет собой амплитуду в начальный момент времени. Начальное смещение зависит от A₀ и также от начальной фазы φ , т.е. x₀=A₀cosφ .

5.7. Коэффициент затухания и логарифмический декремент затухания.

Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно

и называется декрементом затухания .

Для характеристики системы обычно используется колебательной логарифмический декремент затухания , т.е. логарифм декремента затухания

Скорость затухания колебаний определяется величиной называем коэффициентом затухания $$β=$$ .

Найдем время, называемое временем релаксации τ , за которое амплитуда уменьшается в e раз

т. е. коэффициент затухания обратен по величине промежутку времени, за который амплитуда колебаний уменьшается в e раз.

За время релаксации τ система успевает совершить $$N_e=$$ колебаний

Следовательно, $$δ=$$ логарифмический декремент затухания обратно пропорционален по величине числу колебаний, за которые амплитуда колебаний уменьшается в e раз.

Для характеристики колебательной системы используется величина

которая называется добротностью колебательной системы.

Величина Q , пропорциональная числу колебаний, совершаемых системой за время, в течение которого амплитуда колебаний уменьшается в e раз.

5.8. Вынужденные колебания.

До сих пор мы рассматривали свободные колебания, когда выведенная из положения равновесия система совершает колебания будучи предоставленной самой себе. Рассмотрим колебательную систему, которая подвергается действию внешней силы, изменяющейся по гармоническому закону F=F₀cosωt . Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными колебаниями . В этом случае уравнение второго закона Ньютона имеет вид

Учитывая , что a= $$d^2xover dt^2$$ , а υ= $$dxover dt$$ и разделив на массу m , получим

Применив обозначения $$ = ω_0$$ , $$ = 2β$$ и $$ = f_0$$ получим

дифференциальное уравнение вынужденных колебаний.

Будем искать решение уравнения (5.8.3) в виде

предполагая, что результирующее колебание будет совершаться с частотой внешней вынуждающей силы.

Подставим (5.8.4) и (5.8.5) в уравнение (5.8.3)

Чтобы уравнение (69) обратилось в тождество необходимо, чтобы коэффициенты при cosωt и sinωt были равны нулю.

Из выражения (71) получаем

Возведем в квадрат уравнения (70) и сложим

Подставив полученные выражения (71) и (73) в выражение (64) получим уравнение вынужденных колебаний

5.9. Резонанс.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой частоте амплитуда колебаний достигает максимального значения.

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой собственной частоте колебательной системы называется резонансом , а соответствующая частота − резонансной частотой.

Найдем резонансную частоту. Амплитуда вынужденных колебаний будет max, когда выражение $$(ω_0-ω^2)^2 + 4β^2ω^2$$ в уравнении $$A=<f_0over sqrt <(ω_0-ω^2)^2 + 4β^2ω^2>>$$ (5.8.13) будет минимальным.

Продифференцируем это выражение по ω и приравняем к нулю

Полученное уравнение имеет три решения: ω=0 и ω=± $$sqrt <ω_0-2β^2>$$ . 2 . Первое решение соответствует максимуму знаменателя. Из остальных двух решений отрицательное не имеет физического смысла (частота не может быть отрицательной). Таким образом, резонансная циклическая частота

Подставив это значение в выражение для амплитуды (5.8.13), получим выражение для амплитуды при резонансе

Из последнего уравнения (5.9.3) следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность, а резонансная частота, согласно (5.9.2), при тех же условиях (при β=0 ), совпадала бы с собственной частотой колебаний системы ω₀

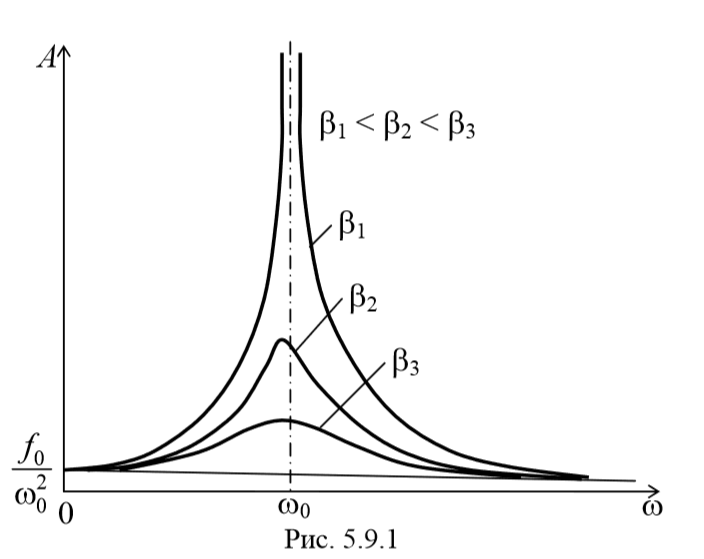
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы показана графически на рис. 5.9.1. В соответствии с (5.9.2) и (5.9.3), чем меньше параметр β , тем выше и правее лежит максимум данной кривой. Изображенная на рис. 5.9.1 совокупность графиков функций (5.8.13), соответствующих различным значениям параметра β , называется резонансными кривыми .

При стремлении ω к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному f₀ω₀ 2 . Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величины F₀

При стремлении ω к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия.

Наконец, отметим, что чем меньше β , тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» получается максимум. При малом затухании (т. е. β ) амплитуда при резонансе приближенно равна A_pes≈f₀/2βω₀ . Разделим это выражение на смещение x₀ из положения равновесия под действием постоянной силы F₀ , равное x₀=f₀/ω_p 2 . В результате получим

где δ = βТ – логарифмический декремент затухания (5.7.2); Q – добротность колебательной системы (5.7.6).

Таким образом, добротность Q показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы. Следует отметить, что это справедливо лишь при небольшом затухании.

Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Гармонические, затухающие, вынужденные колебания. Резонанс (Колебошин С.В.)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке, тема которого «Гармонические, затухающие, вынужденные колебания. Резонанс», мы продолжим изучать различные виды колебательного движения, познакомимся с таким явлением, как резонанс.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Дифференциальные уравнения гармонических колебаний с затуханием и без затухания и их решения

§6 Затухающие колебания

Декремент затухания. Логарифмический декремент затухания.

Добротность

Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.

Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.

Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения

где r — коэффициент сопротивления среды. Знак минус показывает, что F_C направлена в сторону противоположную скорости.

Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r . По второму закону Ньютона

где β — коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.

— дифференциальное уравнение затухающих колебаний.

— у равнение затухающих колебаний.

ω – частота затухающих колебаний:

Период затухающих колебаний:

Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно гово­рить, когда β мало.

Если затухания выражены слабо (β→0), то . Затухающие колебания можно

рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону

В уравнении (1) А₀ и φ₀ — произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания

Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз

τ — время релаксации.

Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D , который равен отношению амплитуд, отстоящих по времени на период:

Логарифмический декремент затухания равен логарифму D :

Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний умень­шилась в е раз. Логарифмический декремент затухания — постоянная для данной системы величина.

Еще одной характеристикой колебательной система является добротность Q .

Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ.

Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии.

Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.

Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.

§7 Вынужденные колебания.

Резонанс

В целом ряде случаев возникает необходимость создания систем, совершающих незатухающие колебания. Получить незатухающие колебания в системе можно, если компенсировать потери энергии, воздействуя на систему периодически изменяющейся силой.

Запишем выражение для уравнения движения материальной точки, совершающей гармоническое колебательное движение под действием вынуждающей силы.

По второму закону Ньютона:

(1)

— дифференциальное уравнение вынуж­денных колебаний.

Это дифференциальное уравнение является линейным неоднородным.

Его решение равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения:

Найдем частное решение неоднородного уравнения. Для этого перепишем уравнение (1) в следующем виде:

(2)

Частное решение этого уравнения будем искать в виде:

т.к. выполняется для любого t , то должно выполняться равенство γ = ω , следовательно,

Это комплексное число удобно представить в виде

где А определяется по формуле (3 ниже), а φ — по формуле (4), следовательно, решение (2),в комплексной форме имеет вид

Его вещественная часть, являвшаяся решением уравнения (1) равна:

(3)

(4)

Слагаемое Х_о.о. играет существенную роль только в начальной стадии при установлении колебаний до тех пор, пока амплитуда вынужденных колебаний не достигнет значения определяемого равенством (3). В установившемся режиме вынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механи­ческой системы, называется резонансом.

Частота ω вынуждающей силы, при которой наблюдается резонанс, называется резонансной. Для того чтобы найти значение ω_рез, необходимо найти условие максимума амплитуды. Для этого нужно определить условие минимума знаменателя в (3) (т.е. исследовать (3) на экстремум).

Зависимость амплитуды колеблющейся величины от частоты вынуждающей силы называется резонансной кривой. Резонансная кривая будет тем выше, чем меньше коэффициент затухания β и с уменьшением β, максимум резонансных кривых смешается вправо. Если β = 0, то

При ω→0 все кривые приходят к значению — статическое отклонение.

Параметрический резонанс возникает в том случае, когда периодическое изменение одного из параметров система приводит к резкому увеличению амплитуды колеблющейся системы. Например, кабины, делающие «солнышко» за счет изменения положения центра тяжести система.(То же в «лодочках».) См. §61 .т. 1 Савельев И.В.

📹 Видео

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Механика. Л 10.1. Колебания. Вывод дифференциального уравнения пружинного маятникаСкачать

70. Затухающие колебанияСкачать

Затухающие колебания Лекция 11-1Скачать

Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Урок 335. Анализ графика гармонических колебанийСкачать

Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

Дифференциальные уравнения, 7 урок, Дифференциальные уравнения, допускающие понижение порядкаСкачать

Дифференциальные уравнения. 11 класс.Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать