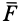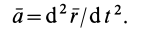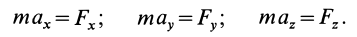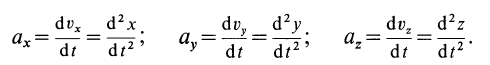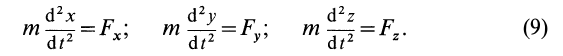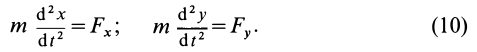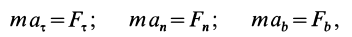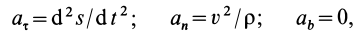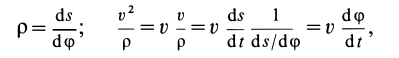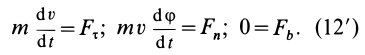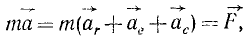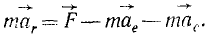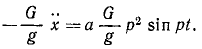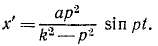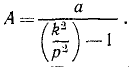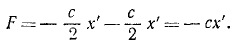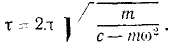Для решения задач динамики используют одну из двух систем уравнений.
- Уравнения в декартовой системе координат
- Уравнения в проекциях на естественные оси координат
- Дифференциальные уравнения движения материальной точки в теоретической механике
- Частные случаи дифференциального уравнения движения материальной точки
- Дифференциальные уравнения относительного движения точки
- Пример решения задачи №1
- Пример решения задачи №2
- Пример решения задачи №3
- ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
- Дифференциальные уравнения движения точки
- Уравнения движения точки в векторном виде
- Уравнения движения точки в координатном виде
- Уравнения движения точки в естественном виде
- iSopromat.ru
- Решение задач, контрольных и РГР
- 📸 Видео
Видео:Дифференциальные уравнения движения точкиСкачать

Уравнения в декартовой системе координат
Движение точки в декартовой системе координат задается уравнениями:
Задачи динамики точки состоят в том, чтобы, зная законы движения, определить действующую наточку силу или, наоборот, зная действующие на точку силы, определить закон движения. Следовательно, для решения задач динамики необходимо, используя второй закон динамики, связать координаты точки и действующие на них силы.
Пусть на материальную точку с массой т действуют силы Fl,F2. Fn. Точка движется в инерциальной системе отсчета 0т.
Основное уравнение динамики точки запишем в виде: та =’LFk и спроецируем обе части равенства на координатные осих, у и z- Учитывая, что
Эти уравнения называются дифференциальными уравнениями движения материальной точки в прямоугольных декартовых координатах.
Если точка движется в плоскости, то взяв координатные оси ох и оу в плоскости движения точки, получим вместо трех два дифференциальных уравнения:
Если точка совершает прямолинейное движение, то получим одно дифференциальное уравнение:
Уравнение (1.54) — дифференциальное уравнение прямолинейного движения точки.
Видео:Дифференциальное уравнение движения материальной точки.Скачать

Уравнения в проекциях на естественные оси координат
Для получения этих уравнений спроецируем обе части уравнения та = ЦРк на касательную, нормаль и бинормаль к траектории.
Уравнение (1.55), где V =
^ > представляет собой дифференциальное уравнение движения точки в проекциях на естественные оси. Они были впервые получены Эйлером и носят название естественных уравнений движения материальной точки. С помощью этих уравнений многие задачи динамики точки, особенно такие, в которых известна ее траектория, решаются проще, чем при помощи уравнений в прямоугольных декартовых координатах.
Видео:Дифференциальные уравнения движения материальной точкиСкачать
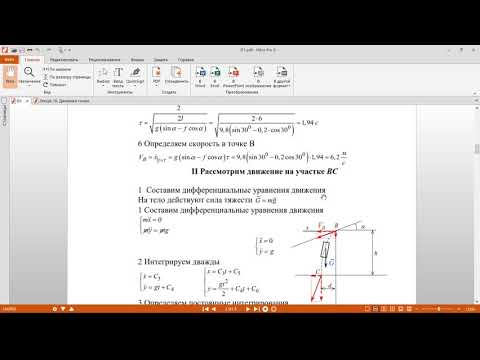
Дифференциальные уравнения движения материальной точки в теоретической механике
Содержание:
Дифференциальные уравнения движения материальной точки:
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей
Из кинематики точки известно, что ускорение 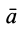
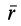
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
Рис. 3
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид
Видео:Динамика. Введение, дифференциальные уравнения движения точки, прямая и обратная задачи динамики.Скачать

Частные случаи дифференциального уравнения движения материальной точки
Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 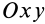
Так как 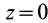
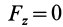
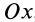
Так как при движении 
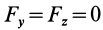
где 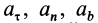
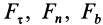
где 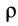
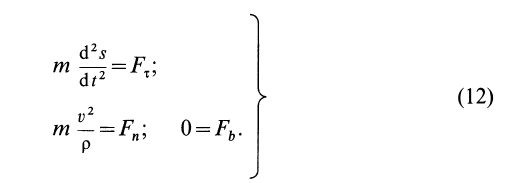
Второе уравнение из (12) можно преобразовать:
где 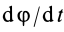
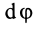
Дифференциальные уравнения (12) можно представить в виде
Рис. 4
Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 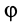
Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.
Видео:Траектория и уравнения движения точки. Задача 1Скачать

Дифференциальные уравнения относительного движения точки
Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения
Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):
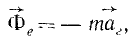
имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.
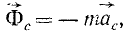
равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.
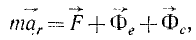
или в проекциях на оси координат:
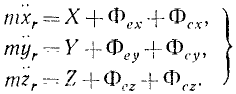
Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.
Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.
Пример решения задачи №1
Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.
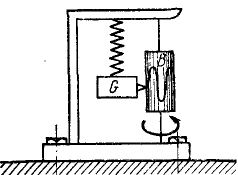
Рис. 171
Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х’ груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:
x’ + k 2 χ’ = ар 2 sin pt.
где 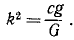
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.
Ответ.
Пример решения задачи №2
Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 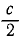
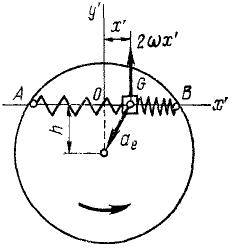
Рис. 172
Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox’ но хорде.
Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х’, то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х’ и направлена к точке О. Следовательно, на ползун действует активная сила
Кроме активной силы, надо учесть действие кориолисовых сил: Φe—переносной и Φc-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 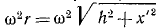
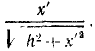
Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx’ и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox’ равна нулю.
При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:
mх’ = — cx’ + mω 2 x’= — (с—mω 2 )x’.
Это уравнение выражает гармоническое колебание с периодом
Ответ. 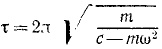
Пример решения задачи №3
Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.
Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.
Поворотная сила ползуна Φс=2mωx’ переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у’, если точка G движется в сторону отрицательных значений х’, т. е, если х’ 2 h. Эта составляющая в рассматриваемом механизме всегда направлена в сторону положительных у’, а потому в суммарном давлении обе кориолисовы силы складываются при х’ 0, и дифференциальное уравнение относительного движения точки имеет вид
mх’ =— (с—mω 2 ) x’ — fm (2ωx’ ± ω2h),
причем знак второго слагаемого в скобках надо брать положительным при х’ 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Д1 Дифференциальные уравнения движения материальной точкиСкачать

ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Динамикой называется раздел механики, в котором изучаются движения материальных точек и материальных тел под действием приложенных к ним сил
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения движения точки
Кинематические характеристики движения точки, изучаемые в кинематике, обусловлены действующими на них силами. Законам движения точки в пространстве соответствуют собственные виды представления дифференциальных уравнений ее движения: векторный, координатный и естественный.
Уравнения движения точки в векторном виде
Уравнения движения материальной точки, масса т которой не изменяется, основаны на втором законе Ньютона
где a — ускорение точки; F — равнодействующая приложенных к точке сил.
Векторное уравнение (8.1) называют основным законом динамики.
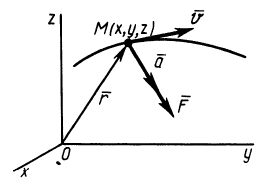
Пусть t — время; О — неподвижная точка
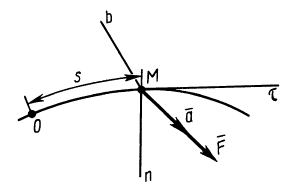
пространства; гиг — радиус вектор ОМ и скорость движения точки М(рис. 8.1). Согласно определениям скорости и ускорения
и равенство (8.1) можно записать в виде
Силы, действующие на точку, могут зависеть от времени, положения точки в пространстве, ее скорости и в некоторых случаях ускорения. Системы отсчета, в которых справедливо уравнение (8.1), называются инерциальными.
Уравнения движения точки в координатном виде
Пусть Oxyz — неподвижная прямоугольная декартова система координат с началом в точке О (рис. 8.2); г и х, у, z — радиус-вектор движущейся точки М и его проекции на координатные оси: г = = ; vx, vy, vz — проекции вектора скорости точки М на координатные оси; X, Y, Z — проекции равнодействующей F приложенных к точке сил на координатные оси: F = <.X, Y, Z>.
Проецируя обе части векторных равенств (8.2) на оси координат, получим три дифференциальных уравнения движения точки в системе декартовых координат:
Величину F равнодействующей силы и углы fix, (Зу, (3Z, образуемые равнодействующей с осями Ox, Оу, Oz координат, можно определить по следующим формулам (рис. 8.2):
При движении точки в плоскости Оху число дифференциальных уравнений движения сокращается до первых двух уравнений, а по
прямой Ох — до одного: = X.
Пусть к свободной точке приложено гг сил F1? F2. Fn; Z), У^, Z* — проекции i-й силы на оси координат: Fj = <Х^,У^, ZJ.
Дифференциальные уравнения (8.3) движения точки можно записать так:
Уравнения движения точки в естественном виде
Пусть траектория движения точки — плоская кривая, и положение точки М на траектории однозначно определяется дуговой координатой s. Напомним обозначения, принятые в кинематике точки: т — орт касательной к траектории точки М п — орт нормали к траектории; vx — проекция скорости точки М на касательную к траектории; аТ> ап — проекции вектора ускорения точки М на оси касательной и главной нормали к траектории; р — радиус кривизны траектории в точке М.
Пусть FT,Fn— проекции равнодействующей F на оси касательной и
нормали (F = Fr + Fn); а — угол образуемый векторами F и т (рис. 8.3).
Спроецируем обе части векторного равенства (8.1) на оси касательной и нормали к траектории:
После подстановки в уравнения (8.6) выражений (2.16) для величин касательного аТ и нормального ап ускорений точки получим
Уравнения (8.7) называются дифференциальными уравнениями движения точки по плоской кривой в естественном виде.
Если траектория точки — не плоская кривая, то к уравнениям (8.7) следует добавить равенство нулю проекции Fp равнодействующей на бинормаль к траектории, перпендикулярную к касательной и нормали (Fp = 0). Это означает, что траектория движения точки такова, что равнодействующая приложенных к ней сил находится в плоскости, натянутой на орты касательной и нормали к траектории.
Видео:Динамика материальной точки в НИСО. Нелинейное дифференциальное уравнение движенияСкачать

iSopromat.ru
Составление систем дифференциальных уравнений движения материальной точки, на которую действует некоторая система сил для определения движения точки под действием этих сил.
Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.
Уравнение второго закона динамики для материальной точки массой m запишется в виде
Спроецировав уравнение (1) на декартовы оси координат, получим систему из трех уравнений
В зависимости от того, что известно о движении точки, дифференциальные уравнения записывают или в декартовых или в естественных координатах.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Видео:Дифференциальные уравнения движения материальной точки. Часть 1Скачать

Решение задач, контрольных и РГР
По желанию можете добавить файл или фото задания
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
📸 Видео
2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Дифференциальные уравнения движенияСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Дифференциальные уравнения поступательного, вращательного и плоского движенияСкачать

Дифференциальные уравнения механической системыСкачать

Теорема об изменении количества движения точкиСкачать

Теоретическая механика. Задание Д1 (часть 1) из сборника ЯблонскогоСкачать