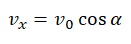Дифференциальные уравнения движения точки брошенной под углом к горизонту (6 видео)

Техническая механика

Содержание

Динамика
Движение материальной точки, брошенной под углом к горизонту
Определение траектории, высоты и дальности полета
Движение тела, брошенного под углом к горизонту
теория по физике 🧲 кинематика
Кинематические характеристики
Тело, брошенное под углом к горизонту с некоторой высоты
Моделирование баллистического движения тела, брошенного под углом к горизонту
💥 Видео

Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

Динамика

Движение материальной точки, брошенной под углом к горизонту

Рассмотрим материальную точку М массой m , брошенную из точки О поверхности Земли с начальной скоростью v₀ под углом α к горизонту (см. рис. 1) .

Определим движение точки М , считая, что на нее действует только сила тяжести G (сопротивлением воздуха пренебрегаем).

Возьмем начало координат в точке О , ось x направим по горизонтали вправо (в направлении траектории, по которой движется точка) , а ось y – по вертикали вверх. Очевидно, что проекция ускорения на ось х будет равна нулю, поскольку единственная сила, действующая на точку — сила тяжести — направлена вертикально вниз (вдоль оси y ), а согласно аксиоме Ньютона, без силы нет и ускорения.
Составим дифференциальные уравнения, описывающие движение точки:

m (d 2 x/dt 2 ) = 0 ; m(d 2 y/dt 2 ) = — mg .

Сокращая равенства на m , получим:

d 2 x/dt 2 = 0 ; (1)
d 2 y/dt 2 = — g . (2)

Интегрируя первое из этих уравнений (1), получим:

dx/dt = С₁ , где С₁ – некоторая произвольная постоянная.

Следовательно, проекция скорости точки М на ось x все время остается величиной постоянной, равной
v_x = v₀ cos α или, на основании результата интегрирования уравнения (1), можно записать:

dx/dt = v₀ cos α.

Интегрируя это уравнение, получаем:

x = v₀t cos α + С₂ .

По условию при t = 0 x = 0 , следовательно, произвольная постоянная С₂ равна нулю.
Окончательно имеем:

x = v₀t cos α.

Интегрируем уравнение (2), находим:

Подставив в это уравнение значение t = 0 , найдем произвольную постоянную С₃ :

С₃ = v_y = v₀ sin α, следовательно:

dy/dt = v₀ sin α – gt .

Интегрируя вторично, получаем:

y = v₀t sin α – gt 2 /2 + C₄ .

Поскольку по условию t = 0 y = 0 , следовательно, произвольная постоянная С₄ равна нулю.
Окончательно получаем:

y = v₀t sin α – gt 2 /2 .

Таким образом становится очевидным, что материальная точка М , брошенная с начальной скоростью v₀ под углом α к горизонту, движется согласно уравнениям:

x = v₀t cos α, (3)
y = v₀t sin α – gt 2 /2 . (4)

Определение траектории, высоты и дальности полета

Для определения траектории точки М исключаем из полученной системы уравнений движения время. Для этого из формулы (3) выражаем время: t = x/(v₀ cos α ) и подставляем это значение в формулу (4).
Получим уравнение траектории:

y = x tg α – gx 2 /(2v₀ 2 cos 2 α ) .

Траектория точки М представляет собой параболу с вертикальной осью симметрии.

Определим время полета точки М , для чего во второе уравнение движения (4) подставим значение y = 0 .
Тогда уравнение движения примет вид:

v₀t sin α – gt 2 /2 = 0 .

Отсюда находим два значения времени t , при которых ордината равна нулю (корни уравнения) :

Первое значение времени соответствует началу полета, второе – конечной точке траектории полета.
Тогда общая продолжительность полета будет равна:

Определим дальность полета по горизонтали, для чего в уравнение движения (3) подставим значение времени t₂ :

x₂ = v₀t cos α = (v₀ cos α ×2v₀ sin α )/g или x₂ = v₀t cos α = (v₀ 2 sin 2 α )/g .

Из полученного уравнения можно сделать вывод, что максимальная дальность полета x_max имеет место при sin2 α = 1 , т. е. при α = π/4 рад :

Определим наибольшую высоту подъема точки М , т. е. ее ординату в тот момент времени t₁ , когда проекция скорости на ось y окажется равной нулю:

dy/dt = v_y = v₀ sin α – gt₁ = 0 .

Из полученного равенства определим t₁ :

t₁ = (v₀ sin α )/g = t 2 /2 .

Следовательно, наибольший подъем точки имеет место в середине пути полета, при x₁ = x 2 /2 .

Подставив значение t₁ в уравнение (4), получим:

y₁ = (v₀ sin α ×v₀ sin α )/g – gv₀ 2 sin 2 α /(2g 2 ) .

Из полученного уравнения можно сделать вывод, что максимальной высоты точка достигает при sin α = 1 или при α = π/2 рад , т. е. когда точка брошена под углом 90˚ к горизонту (вертикально вверх) .

Полученные формулы и зависимости позволяют решать различные задачи на движение тел и точек под действием силы тяжести в приближенной форме, поскольку они не учитывают силы сопротивления движению со стороны воздуха (аэродинамическое сопротивление).

Видео:Движение тела, брошенного под углом к горизонтуСкачать

Движение тела, брошенного под углом к горизонту

теория по физике 🧲 кинематика

Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.

Важные факты! График движения тела, брошенного под углом к горизонту:

α — угол, под которым было брошено тело

Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v_0x = v₀cosα. Ее проекция на ось ОУ равна v_0y = v₀sinα.
Проекция мгновенной скорости на ось ОХ равна: v_x = v₀ cosα. Ее проекция на ось ОУ равна нулю: v_y = v₀ sinα – gt.
Проекция ускорения свободного падения на ось ОХ равна нулю: g_x = 0. Ее проекция на ось ОУ равна –g: g_y = –g.

Видео:Д1 Дифференциальные уравнения движения материальной точкиСкачать

Кинематические характеристики

Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:

Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:

Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:

Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: v_y = 0. Время подъема определяется следующей формулой:

Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:

Подставляя в выражение формулу полного времени полета, получаем:

Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:

Учитывая, что x₀ = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v₀ cosα, данная формула принимает вид:

Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:

Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v₀ sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:

Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:

Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?

Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:

Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:

Видео:Кинематика: Тело, брошенное под углом к горизонтуСкачать

Тело, брошенное под углом к горизонту с некоторой высоты

Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.

График движения тела, брошенного под углом к горизонту с некоторой высоты:

Время падения тела больше времени его подъема: t_пад > t_под.

Полное время полета равно:

Уравнение координаты x:

Уравнение координаты y:

Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.

Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:

x = v₀ cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.

Алгоритм решения

Решение

Запишем исходные данные:

Построим чертеж и укажем на нем все необходимое:

Нулевой уровень — точка D.

Закон сохранения энергии:

Потенциальная энергия шарика в точке А равна:

Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.

В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:

Перед ударом кинетическая энергия шарика равна:

Согласно закону сохранения энергии:

E p A = E p B + E k B

m g H = m g l 1 + m v 2 2 . .

Отсюда высота H равна:

H = m g l 1 m g . . + m v 2 2 m g . . = l 1 + v 2 2 g . .

Относительно точки В шарик поднимется на высоту h – l₁. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:

h − l 1 = v 2 sin 2 . β 2 g . . = v 2 sin 2 . ( 90 − 2 α ) o 2 g . .

l 1 = h − v 2 sin 2 . ( 90 − 2 α ) o 2 g . .

Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:

H = l 1 + v 2 2 g . . = h − ( g t ) 2 sin 2 . ( 90 − 2 α ) o 2 g . . + ( g t ) 2 2 g . .

H = h − g t 2 sin 2 . ( 90 − 2 α ) 2 . . + g t 2 2 . . = h − g t 2 2 . . ( sin 2 . ( 90 − 2 α ) o − 1 )

H = 1 , 4 − 10 · 0 , 4 2 2 . . ( sin 2 . ( 90 − 6 0 ) o − 1 )

H = 1 , 4 − 5 · 0 , 16 ( sin 2 . 3 0 o − 1 )

H = 1 , 4 − 0 , 8 ( ( 1 2 . . ) 2 − 1 ) = 1 , 4 − 0 , 8 ( 1 4 . . − 1 )

H = 1 , 4 + 0 , 6 = 2 ( м )

pазбирался: Алиса Никитина | обсудить разбор | оценить

В момент t=0 мячик бросают с начальной скоростью v₀ под углом α к горизонту с балкона высотой h (см. рисунок).

Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).

К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.

Алгоритм решения

Решение

Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.

Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.

Координата x меняется согласно уравнению координаты x:

Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:

Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:

В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.

Формула проекции скорости мячика на ось ОХ:

Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.

Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.

Остается последний вариант — координата y. Уравнение этой координаты имеет вид:

Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.

Теперь записываем установленные соответствия в порядке АБ: 42.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?

Для каждой величины определите соответствующий характер изменения:

увеличивается
уменьшается
не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Сделать чертеж, иллюстрирующий ситуацию.
Записать формулы, определяющие указанные в условии задачи величины.
Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.

Решение

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).

Горизонтальная составляющая скорости шарика определяется формулой:

Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).

Ответом будет следующая последовательность цифр — 33.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Видео:Бросок под углом к горизонтуСкачать

Моделирование баллистического движения тела, брошенного под углом к горизонту

1 Моделирование баллистического движения тела, брошенного под углом к горизонту Автор: Вовчок Сергей Школа: ГБОУ Школа Перспектива, г. Москва Класс: 10А Руководитель: Сметанкин А. Б., учитель физики

2 В школьном курсе физики рассматривается модель движения тела, брошенного под углом к горизонту, полученная Галилео Галилеем. Согласно этой модели траекторией движения тела (материальной точки) является парабола, а сложное движение представляется в виде суммы простых: равномерного движения по горизонтали и равноускоренного по вертикали. y 0 v 0 α x = v 0 cos α t y = v 0 sin α t gt2 2 v α 1 h y = tgα x g 2 v 0 cos α 2 x2 l x v x = v 0 cos α v y = v 0 sin α gt t пол = 2v 0 sin α g l = v 0 2 sin 2α g h = v 0 2 sin 2 α 2g 2

3 Движение реального тела в среде отличается от классического решения. С ростом начальной скорости степень влияния среды становится существенной, и траектория сильно изменяется. При этом дальность и высота полёта, а также его время не согласуются с формулами, для решения Галилея (см. слайд 2). Достаточно сказать, что дальность полёта может получаться завышенной в 10 и более раз! 3

4 Для того, чтобы учащиеся имели представление о том, какова траектория движения тела при наличии силы сопротивления со стороны среды у учителя должна быть возможность быстро смоделировать данный процесс в ходе урока. Из-за сложности задачи её решение целесообразно осуществлять с помощью компьютерного моделирования (разработки вычислительной программы). Наличие такой программы будет способствовать большей наглядности учебного процесса. 4

5 Задача о движении тела, брошенного под углом к горизонту, с учётом силы сопротивления среды в аналитической форме решена Бернулли и Эйлером. Это решение, однако, слишком сложно для того, чтобы его можно было использовать в рамках школьного учебного процесса. Основная идея для получения нашего приближённого решения использование хорошо известного школьникам второго закона Ньютона, в который добавляется сила сопротивления среды, как ещё одна из сил, действующих на тело (решение Бернулли и Эйлера не основаны на упомянутом законе). С помощью такого приближённого решения можно получить достаточно качественные результаты, иллюстрирующие суть процесса. 5

6 Второй закон Ньютона при наличии силы сопротивления для рассматриваемого движения тела массой m имеет вид mg + F c = ma. Практика показывает, что сила сопротивления F c при высокой скорости пропорциональна скорости движения тела, а при очень высокой скорости её квадрату. Поэтому целесообразно рассмотреть эти два случая. 1. Сила сопротивления пропорциональна скорости движения F с = kv. Векторное уравнение (см. выше) в проекциях на координатные оси приводит к системе уравнений (k коэффициент сопротивления среды) dv x dt = k m v x dv y dt = g k m v y. (1) 6

7 2. Сила сопротивления пропорциональна квадрату скорости F с = k v v Векторное уравнение в проекциях на координатные оси приводит к системе уравнений dv x dt = k m v x 2 + v y2 v x dv y dt = g k m v x 2 + v y2 v y. (2) Система (1) является линейной системой дифференциальных уравнений, имеющей решение (изучается в высшей школе), система (2) система нелинейных дифференциальных уравнений, решение которой может быть получено лишь приближённо с помощью численных процедур. 7

8 Работа проводилась в три этапа. 1. Разработка алгоритма вычислительной программы для классического решения Галилея. 2. Решение систем (1) и (2) и реализация их расчёта в программе. 3. Программирование. 8

9 Первый этап (движение без учёта сопротивления). Реализация готового решения Галилея осуществлялась следующим образом. Траектория движения y(x) строится согласно выражениям, показанным на слайде номер 2 по введённым пользователем значениям v 0 и a. При этом выбирается достаточно малое значение шага по времени Dt. Цикл программы проходит все значения для t от 0 до времени падения t пад, с шагом Dt. Скорости для тех же промежутков времени находятся по выражениям, также показанным на слайде 2. Второй этап (учёт силы сопротивления) 1. Решение системы (1) для координат и скоростей даёт x = v 0x m k y = m k 1 k e m t v 0y + mg k 1 e k m t gt ; (3) 9

10 v x = v 0x e k m t v y = v 0y e k m t gm k 1 e k m t, v 0x = v 0 cosa, v 0y = v 0 sina. (4) Реализация в вычислительной программе траектория движения y(x) строится согласно выражениям (3) по введённым пользователем значениям v 0, a, m и k. При этом выбирается достаточно малое значение шага по времени Dt. Цикл программы проходит с шагом Dt все значения для t от 0 до времени падения t пад, которое изначально неизвестно и находится приближённо с помощью специальной процедуры в отдельном цикле. Скорости рассчитываются по формулам (4). 10

11 Второй этап (учёт силы сопротивления, продолжение) 2. Для приближённого решения системы (2) производные заменяем приращениями, что в итоге приводит к решению в виде: v x t + t v x t k m v x 2 t + v2 y t v x t t v x t + t v y t g k m v x 2 t + v2 y t v y t t, (5) x t + t x t + v x t t y t + t y t + v y t t. Реализация в вычислительной программе. Проекции скоростей находим по формулам (5). Цикл программы проходит с шагом Dt все значения для t от 0 до времени падения t пад, которое изначально неизвестно и находится приближённо. Время падения вычисляется также, как и в предыдущем случае при помощи отдельного цикла с малым шагом Dt. Траектория строится согласно формулам (6). (6) 11

12 Третий этап (программирование) Программа написана на языке Си++. Для расширения функциональности было решено кроме построения графика, показывающего траекторию движения тела, добавить возможность просмотра основных кинематических и энергетических характеристик тела в любой предшествующий промежуток времени полёта (с шагом Dt). Пользователю доступны значения координат x и y, проекций скоростей v x и v y, а также значения кинетической и потенциальной энергии тела, вычисляемые по известным формулам E к t = mv2 t 2, E p t = mgh t = mgy t. 12

13 В ходе проекта была разработана вычислительная программа, позволяющая моделировать три варианта движения: без учёта сопротивления среды, с учётом сопротивления среды (сила пропорциональна скорости и квадрату скорости движения). Графический интерфейс программы показан на рисунке справа. 13

14 На данных рисунках демонстрируются результаты работы программы при учёте влияния сопротивления среды. 14

15 Разработанная программа может быть использована в учебном процессе для качественного объяснения закономерностей движения тела, брошенного под углом к горизонту, а также для самостоятельной исследовательской работы учащихся. Автору не известны аналогичные программы, полностью подобные по реализованному функциональному наполнению. 15