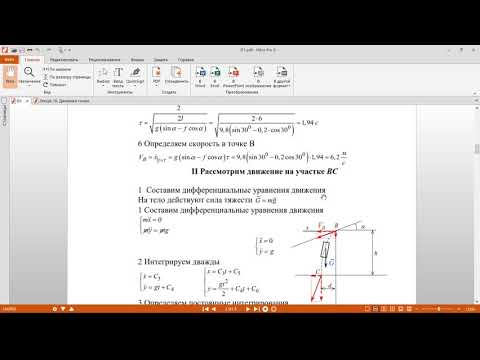
При векторном способе задания движения:
, 
, 
.
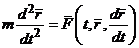
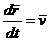
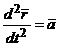
В координатной форме:
В естественной форме:
Интегрируя дважды по времени, получаем уравнения движения точки в координатной форме. Постоянные интегрирования определяют с использованием начальных (граничных) условий:
При t = 0 
Задача Д1
Дифференциальные уравнения движения несвободной материальной точки
В этом случае используется принцип освобождаемости от связей: движение несвободной материальной точки не изменится, если ее сделать свободной и заменить связи их реакциями.
, 
— реакция связи.
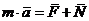
Задача Д2
СИЛА ИНЕРЦИИ МТ. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МТ
Рассматривается движение МТ М под действием силы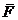 
, приложенной к ней со стороны тела А — ускоряющего тела.
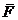
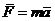
Если ускоряющих тел несколько, то — равнодействующая. Эта сила определяется уравнением
.
В соответствии с законом о равенстве действия и противодействия точка М действует на тело А с силой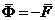 
. Поэтому
— сила инерции МТ.
Проекции силы инерции на декартовы оси и оси Эйлера
, 
, 
, 
, 
.
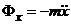
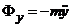
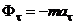
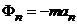
Пусть несвободная МТ М движется в инерциальном пространстве Oxyz.
Основное уравнение динамики для нее имеет вид
.
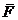
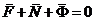
Здесь и — равнодействующие заданных сил и реакций связей. Тогда
.
Принцип Даламбера для МТ: Заданные силы и реакции связей, под действием которых движется точка, и сила инерции точки образуют уравновешенную систему сил
.
ДИНАМИЧЕСКИЕ МЕРЫ МАТЕРИАЛЬНЫХ ОБЪЕКТОВ
Динамическими мерами являются:
— момент количества движения (кинетический момент);
Масса, момент инерции – меры инертности МО, остальные – динамические меры механического движения МО.
Масса, центр масс МСМТ
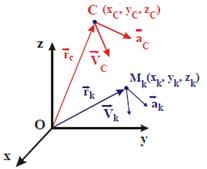
Пусть в пространстве Oxyz рассматривается движение МСМТ <Mk>n с массами <mk>n, положение которых определяется радиус-векторами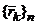 
.
Массой МСМТ называется величина, равная сумме масс точек системы
.
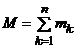
Центром масс (ЦМ) МСМТ называется точка С пространства Oxyz, радиус-вектор которой в каждый момент времени равен
.
, 
, 
.
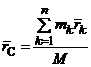
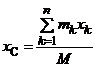
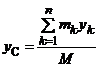
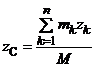
Моменты инерции МСМТ и ТТ
Момент инерции МСМТ относительно оси (осевой момент инерции) – сумма произведений масс всех точек системы на квадраты их расстояний до этой оси:
,
,
.
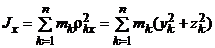
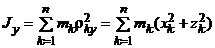
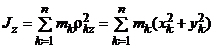
Момент инерции МСМТ относительно центра О (полярный моментом инерции) — сумма произведений масс всех точек системы на квадраты их расстояний до центра:
.
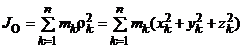
Осевые и полярный моменты инерции характеризуют разброс точек МС относительно оси и центра.
Центробежный момент инерции МСМТ — сумма произведений масс всех точек системы на координаты этих точек вдоль двух осей:
,
,
.
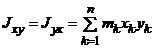
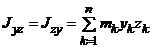
Центробежные моменты инерции характеризуют асимметрию распределения МТ относительно координатных плоскостей.
Радиусом инерции МСМТ (ТТ) относительно оси l
.
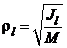
Зная радиус инерции, момент инерции МСМТ (ТТ)
.
Видео:Дифференциальные уравнения движения точкиСкачать
Задачи динамики для свободной и несвободной материальной точки
Динамика точки.
В данной лекции рассматриваются следующие вопросы:
1. Динамика точки.
2. Основные понятия и определения.
3. Законы динамики.
4. Задачи динамики для свободной и несвободной материальной точки.
5. Дифференциальные уравнения движения точи.
6. План решения второй задачи движения.
7. Движение точки, брошенной под углом к горизонту в однородном поле тяжести.
8. Относительное движение материальной точки.
9. Влияние вращения Земли на равновесие и движение тел.
10. Общие теоремы динамики точки.
11. Количество движения.
12. Импульс силы.
Динамика точки. Основные понятия и определения.
Динамикой называется раздел механики, в котором изучаются законы движения материальных тел под действием сил.
Как показывает опыт, переменные силы могут определенным образом зависеть от времени, от положения тела и от его скорости. В частности, от времени зависит сила тяги электровоза при постепенном выключении или включении реостата; от положения тела зависит сила упругости пружины; от скорости движения зависят силы сопротивления среды (воды, воздуха).
К понятию об инертности тел мы приходим, сравнивая результаты действия одной и той же силы на разные материальные тела. Опыт показывает, что если одну и ту же силу приложить к двум разным, свободным от других воздействий покоящимся телам, то в общем случае по истечении одного и того же промежутка времени эти тела пройдут разные расстояния и будут иметь разные скорости.
Инертность и представляет собой свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил. Если, например, при действии одинаковых сил изменение скорости первого тела происходит медленнее, чем второго, то говорят, что первое тело является более инертным, и наоборот.
Количественной мерой инертности данного тела является физическая величина, называемая массой тела. В механике масса т рассматривается как величина скалярная, положительная и постоянная для каждого данного тела.
В общем случае движение тела зависит не только от его суммарной массы и приложенных сил; характер движения может еще зависеть от формы тела, точнее от взаимного расположения образующих его частиц (т. е. от распределения масс).
Материальной точкой называют материальное тело (тело, имеющее массу), размерами которого при изучении его движения можно пренебречь.
Законы динамики
Первый закон (закон инерции), открытый Галилеем, гласит: изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить это состояние. Движение, совершаемое точкой при отсутствии сил, называется движением по инерции.
Второй закон (основной закон динамики) гласит: произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы.
Математически этот закон выражается векторным равенством 
.
При этом между модулями ускорения и силы имеет место зависимость ma = F.
Третий закон (закон равенства действия и противодействия) устанавливает характер механического взаимодействия между материальными телами. Для двух материальных точек он гласит: две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.
Заметим, что силы взаимодействия между свободными материальными точками (или телами), как приложенные к разным объектам, не образуют уравновешенной системы.
Задачи динамики для свободной и несвободной материальной точки.
Для свободной материальной точки задачами динамики являются следующие: 1) зная закон движения точки, определить действующую на нее силу (первая задача динамики); 2) зная действующие на точку силы, определить закон движения точки (вторая или основная задача динамики).
Решаются обе эти задачи с помощью уравнений, выражающих основной закон динамики, так как эти уравнения связывают ускорение 
т.е. величину, характеризующую движение точки, и действующие на нее силы.
Пример 2.Лифт весом Р (рис.3) начинает подниматься с ускорением 
. Определить натяжение троса.
Рис. 3
Рассматривая лифт как свободный, заменяем действие связи (троса) реакцией Т и, составляя уравнение 
в проекции на вертикаль, получаем:
.
Отсюда находим: 
.
Если лифт начнёт опускаться с таким же ускорением, то натяжение троса будет равно:
.
Видео:Д1 Дифференциальные уравнения движения материальной точкиСкачать
Дифференциальные уравнения движения свободной и несвободной МТ. Две задачи динамики точки
Читайте также:
|
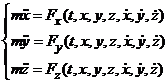
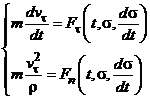
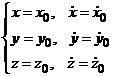
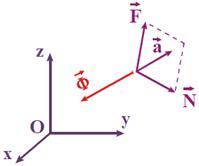
– равнодействующая системы сил (активных и реакций), действующих на точку.
(1)
,
. (2)
, 
, 
,
(3)
) и использовав соотношения, определяющие формулы для ускорения точки при естественном способе задания движения:
, 
, 
,
(4)
.
(5)
(6)
(7)
(8)
– значения координат МТ и их производных в начальный момент времени t=0.
(9)
. (g = 1,2,…,6)
