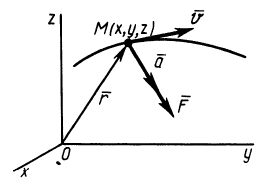
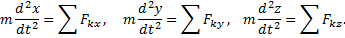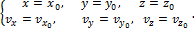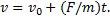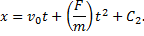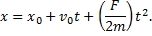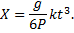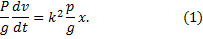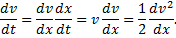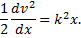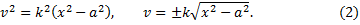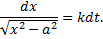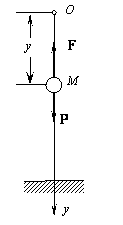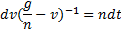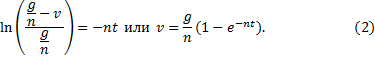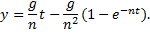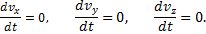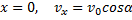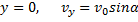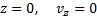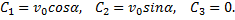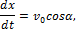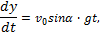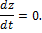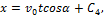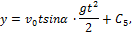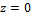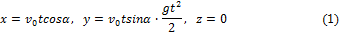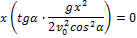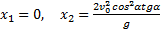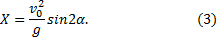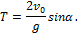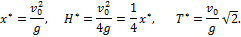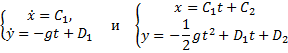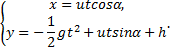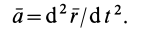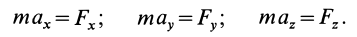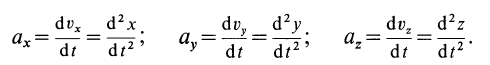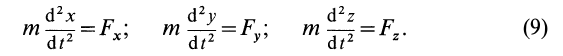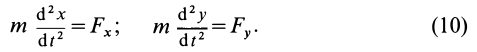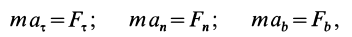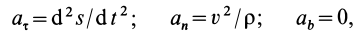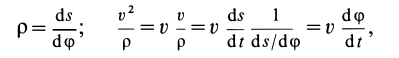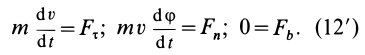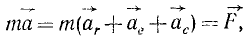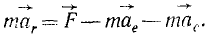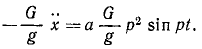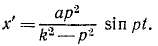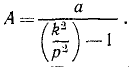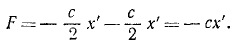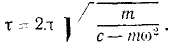С помощью дифференциальных уравнений движения решается вторая задача динамики. Правила составления таких уравнений зависят от того, каким способом хотим определить движение точки.
1) Определение движения точки координатным способом.
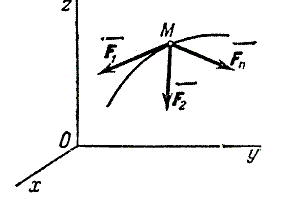
Рассмотрим свободную материальную точку, движущуюся под действием сил 
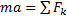
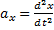
Рис.20
Так как действующие на точку силы могут зависеть от времени, от положения точки и от ее скорости, то правые части уравнений могут содержать время t, координаты точки х, у, z и проекции ее скорости 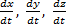
Чтобы с помощью этих уравнений решить основную задачу динамики, надо, кроме действующих сил, знать еще начальные условия, т.е. положение и скорость точки в начальный момент. В координатных осях Oxyz начальные условия задаются в виде: при t=0
Зная действующие силы, после интегрирования уравнений найдем координаты х, y, z движущейся точки, как функции времени t, т.е. найдем закон движения точки.
Пример 17. Найти закон движения материальной точки массы m, движущейся вдоль оси х под действием постоянной по модулю силы F (рис. 20.1) при начальных условиях: 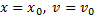
Рис.20.1
Решение. Составим дифференциальное уравнение движения точки в проекции на ось х: 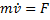
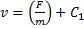
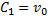
Далее, учитывая, что v = dx/dt, приходим к дифференциальному уравнению: 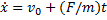
Постоянную C2 определяем из начального условия для координаты точки. Она равна 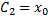
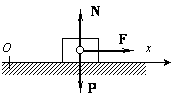
Пример 18. Груз веса Р (рис.20.2) начинает двигаться из состояния покоя вдоль гладкой горизонтальной плоскости под действием силы F = kt. Найти закон движения груза.
Рис.20.2
Решение. Выберем начало отсчета системы координат О в начальном положении груза и направим ось х в сторону движения (рис. 20.2). Тогда начальные условия имеют вид: x(t = 0) = 0, v(t = 0) = 0. На груз действуют силы F, P и сила реакции плоскости N. Проекции этих сил на ось х имеют значения Fx = F = kt, Рx = 0, Nx = 0, поэтому соответствующее уравнение движения можно записать так: 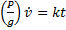
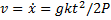
Последнее выражение, в свою очередь, является дифференциальным уравнением, интегрируя которое найдем закон движения материальной точки: 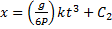
Пример 19. На груз, находящийся в покое на горизонтальной гладкой плоскости (см. рис. 20.2) на расстоянии a от начала координат, начинает действовать в положительном направлении оси x сила F = k 2 (P/g)x, где Р – вес груза. Найти закон движения груза.
Решение. Уравнение движения рассматриваемого груза (материальной точки) в проекции на ось х
Начальные условия уравнения (1) имеют вид: x(t = 0) = a, v(t = 0) = 0.
Входящую в уравнение (1) производную по времени от скорости представим так
Подставляя это выражение в уравнение (1) и сокращая на (P/g), получим
Разделяя переменные в последнем уравнении, находим, что 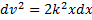
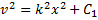
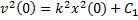
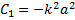
Поскольку сила действует на груз в положительном направлении оси х, то ясно, что в том же направлении он должен и двигаться. Поэтому в решении (2) следует выбрать знак «плюс». Заменяя дальше во втором выражении (2) v на dx/dt, получаем дифференциальное уравнение для определения закона движения груза. Откуда, разделяя переменные, имеем
Интегрируя последнее, находим: arch x/a=kt+C2. После нахождения постоянной C2 окончательно получаем
arch x/a=kt или 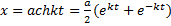
Пример 20. Шар M массы m (рис.20.3) падает без начальной скорости под действием силы тяжести. При падении шар испытывает сопротивление 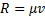
Рис.20.3
Решение. Введем систему координат с началом в точке местоположения шара при t = 0, направив ось у вертикально вниз (рис. 20.3). Дифференциальное уравнение движения шара в проекции на ось у имеет тогда вид
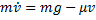
Начальные условия для шара записываются так: y(t = 0) = 0, v(t = 0) = 0.
Разделяя переменные в уравнении (1)
и интегрируя, находим: 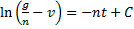
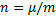
Отсюда следует, что предельная скорость, т.е. скорость при 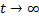
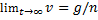
Чтобы найти закон движения, заменим в уравнении (2) v на dy/dt. Тогда, интегрируя полученное уравнение с учетом начального условия, окончательно находим
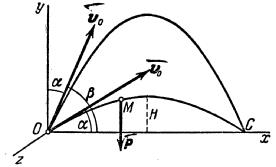
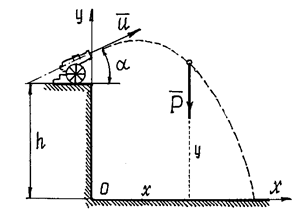
Пример 21. Изучим движение тела, брошенного с начальной скоростью v0 под углом 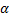
Рис.21
Поместим начало координат О в начальном положении точки. Направим ось Oy вертикально вверх; горизонтальную ось Ox расположим в плоскости, проходящей через Оy и вектор v0, а ось Oz проведём перпендикулярно первым двум осям (рис.21). Тогда угол между вектором v0 и осью Ox будет равен 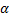
Изобразим движущуюся точку М где-нибудь на траектории. На точку действует одна только сила тяжести 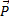
Подставляя эти величины в дифференциальные уравнения и замечая, что 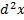
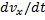
Умножая обе части этих уравнений на dt и интегрируя, находим:
Начальные условия в нашей задаче имеют вид:
Удовлетворяя начальным условиям, будем иметь:
Подставляя эти значения С1, С2 и С3 в найденное выше решение и заменяя vx, vy, vz на 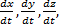
Интегрируя эти уравнения, получим:
Подстановка начальных данных даёт С4=С5=С6=0, и мы окончательно находим уравнения движения точки М в виде:
Из последнего уравнения следует, что движение происходит в плоскости Оxy.
Имея уравнение движения точки, можно методами кинематики определить все характеристики данного движения.
1. Траектория точки. Исключая из первых двух уравнений (1) время t, получим уравнение траектории точки:
Это — уравнение параболы с осью, параллельной оси Оy. Таким образом, брошенная под углом к горизонту тяжёлая точка движется в безвоздушном пространстве по параболе (Галилей).
2. Горизонтальная дальность. Определим горизонтальную дальность, т.е. измеренное вдоль оси Оx расстояние ОС=Х. Полагая в равенстве (2) y=0, найдём точки пересечения траектории с осью Ох. Из уравнения:
получаем
Первое решение дает точку О, второе точку С. Следовательно, Х=Х2 и окончательно
Из формулы (3) видно, что такая же горизонтальная дальность X будет получена при угле 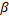
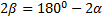
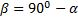
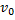
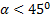
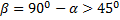
При заданной начальной скорости V0 наибольшая горизонтальная дальность в безвоздушном пространстве получается, когда 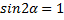
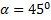
3. Высота траектории. Если положить в уравнении (2)
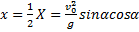
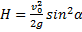
4. Время полета. Из первого уравнения системы (1) следует, что полное время полета Т определяется равенством 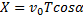
При угле наибольшей дальности 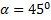
Полученные результаты практически вполне приложимы для ориентировочного определения характеристик полета снарядов (ракет), имеющих дальности порядка 200…600 км, так как при этих дальностях (и при 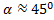
Пример 22. Из пушки, установленной на высоте h, произвели выстрел под углом 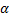
Рис.22
Чтобы правильно составить дифференциальные уравнения движения, надо решать подобные задачи по определённой схеме.
а) Назначить систему координат (количество осей, их направление и начало координат). Удачно выбранные оси упрощают решение.
б) Показать точку в промежуточном положении. При этом надо проследить за тем, чтобы координаты такого положения обязательно были положительными (рис.22).
в) Показать силы, действующие на точку в этом промежуточном положении (силы инерции не показывать!).
В этом примере – это только сила 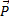
г) Составить дифференциальные уравнения по формулам: 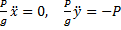
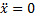
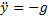
д) Решить дифференциальные уравнения.
Полученные здесь уравнения – линейные уравнения второго порядка, в правой части – постоянные. Решение этих уравнений элементарно.
Осталось найти постоянные интегрирования. Подставляем начальные условия (при t = 0 x = 0, y = h, 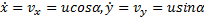
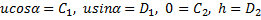
Подставляем в уравнения значения постоянных и записываем уравнения движения точки в окончательном виде
Имея эти уравнения, как известно из раздела кинематики, можно определить и траекторию движения ядра, и скорость, и ускорение, и положение ядра в любой момент времени.
Как видно из этого примера, схема решения задач довольно проста. Сложности могут возникнуть только при решении дифференциальных уравнений, которые могут оказаться непростыми.
Видео:Дифференциальное уравнение движения материальной точки.Скачать

Дифференциальные уравнения движения материальной точки в теоретической механике
Содержание:
Дифференциальные уравнения движения материальной точки:
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей
Из кинематики точки известно, что ускорение 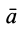
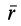
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
Рис. 3
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид
Видео:Дифференциальные уравнения движения материальной точкиСкачать
Частные случаи дифференциального уравнения движения материальной точки
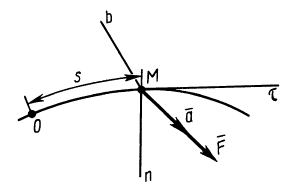
Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 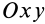
Так как 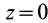
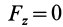
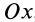
Так как при движении 
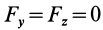
где 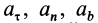
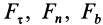
где 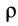
Второе уравнение из (12) можно преобразовать:
где 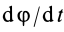
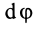
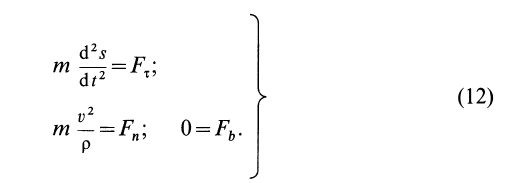
Дифференциальные уравнения (12) можно представить в виде
Рис. 4
Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 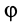
Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.
Видео:Дифференциальные уравнения движения точкиСкачать

Дифференциальные уравнения относительного движения точки
Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения
Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):
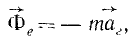
имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.
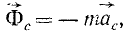
равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.
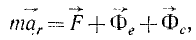
или в проекциях на оси координат:
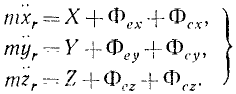
Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.
Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.
Пример решения задачи №1
Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.
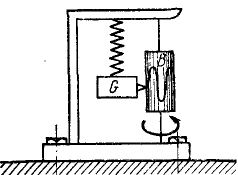
Рис. 171
Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х’ груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:
x’ + k 2 χ’ = ар 2 sin pt.
где 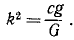
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.
Ответ.
Пример решения задачи №2
Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 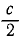
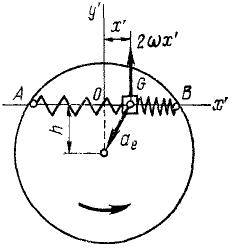
Рис. 172
Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox’ но хорде.
Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х’, то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х’ и направлена к точке О. Следовательно, на ползун действует активная сила
Кроме активной силы, надо учесть действие кориолисовых сил: Φe—переносной и Φc-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 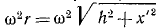
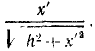
Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx’ и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox’ равна нулю.
При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:
mх’ = — cx’ + mω 2 x’= — (с—mω 2 )x’.
Это уравнение выражает гармоническое колебание с периодом
Ответ. 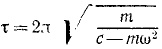
Пример решения задачи №3
Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.
Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.
Поворотная сила ползуна Φс=2mωx’ переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у’, если точка G движется в сторону отрицательных значений х’, т. е, если х’ 2 h. Эта составляющая в рассматриваемом механизме всегда направлена в сторону положительных у’, а потому в суммарном давлении обе кориолисовы силы складываются при х’ 0, и дифференциальное уравнение относительного движения точки имеет вид
mх’ =— (с—mω 2 ) x’ — fm (2ωx’ ± ω2h),
причем знак второго слагаемого в скобках надо брать положительным при х’ 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:РГР Д1 Обратная задача динамикиСкачать

iSopromat.ru
Составление систем дифференциальных уравнений движения материальной точки, на которую действует некоторая система сил для определения движения точки под действием этих сил.
Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.
Уравнение второго закона динамики для материальной точки массой m запишется в виде
Спроецировав уравнение (1) на декартовы оси координат, получим систему из трех уравнений
В зависимости от того, что известно о движении точки, дифференциальные уравнения записывают или в декартовых или в естественных координатах.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
🎦 Видео
Д1 Дифференциальные уравнения движения материальной точкиСкачать

Дифференциальные уравнения движения материальной точки. Часть 1Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения движенияСкачать

Лекция №1 "Кинематика материальной точки" (Булыгин В.С.)Скачать

Дифференциальные уравнения движения материальной точки. Часть 2Скачать

Динамика. Введение, дифференциальные уравнения движения точки, прямая и обратная задачи динамики.Скачать

Теоретическая механика. Задание Д1 (часть 1) из сборника ЯблонскогоСкачать

Динамика материальной точки в НИСО. Нелинейное дифференциальное уравнение движенияСкачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать

Динамика точки. Законы Галилея-НьютонаСкачать

Практика_№8_Динамика_материальной_точки_2_часаСкачать

Теоретическая механика. Задание Д2 (часть 1) из сборника ЯблонскогоСкачать