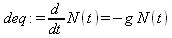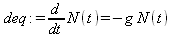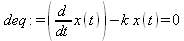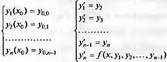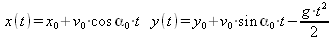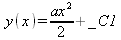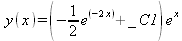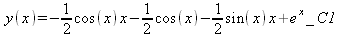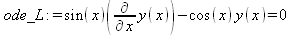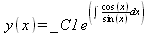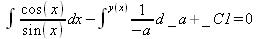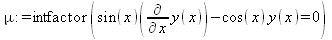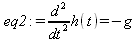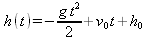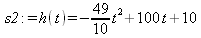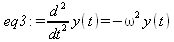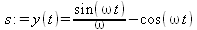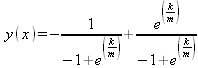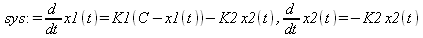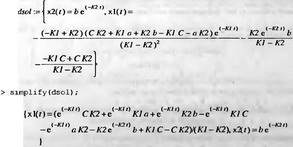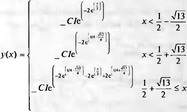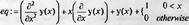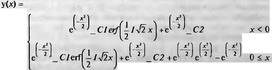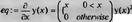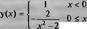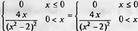Дифференциальные уравнения частных производных maple

Новая версия программы Maple «способна» решать аналитически некоторые классы дифференциальных уравнений в частных производных. Для этого введена команда pdesolve ( уравнения, переменные).

В решении этого уравнения присутствуют произвольные функции _F1, _F2.

Maple находит решение некоторых видов уравнений с непостоянными коэффициентами, например

Неоднородное уравнение для функции U от трех независимых переменных

> pdesolve( diff(U(x, y, z), x)+2*diff(U(x, y, z), y)+5*diff(U(x, y, z),
z)=13*x*y*z, U(x, y, z) );

Следующие два примера уравнений математической физики.

Команда pdesolve «в лоб» не решает это уравнение, действительно

Применим известный прием разделения переменных. Для этого вначале сделаем подстановку

Теперь разделим обе части уравнения на X(x)*T(t)

Так как в левой и правой частях полученного равенства стоят функции от разных переменных, то правая и левая части являются постоянными величинами.

Теперь мы получили обыкновенное дифференциальное уравнение и его решение

Аналогично приравняем константе правую часть равенства

Решение полученного обыкновенного дифференциального уравнения

Для упрощения выполним подстановку конкретных значений для произвольных постоянных

Преобразуем к тригонометрическому виду

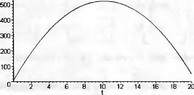
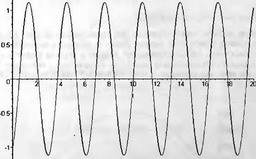
Теперь можно построить график первого решения (рис. 9).

Проверим правильность первого решения

В качестве еще одного примера рассмотрим волновое уравнение

Найдем решение для u(x,t).

Здесь _F1 и _F2 — произвольные функции. Заменим их конкретными функциями f1 и f2

Заменим наименования функций в решении на f1 и f2, а также положим с=1.

Теперь подставим значения f1 и f2 в u(x,t), чтобы получить конкретное решение.

Применим функцию unapply, чтобы превратить полученное выражение в функцию от x и t

Теперь мы можем построить график решения (рис. 10).

На графике мы видем две волны, которые представляют решение волнового уравнения.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:Линейные дифференциальные уравнения в частных производныхСкачать

Частные производные

Для вычисления частных производных применяется процедура diff (). В случае функции нескольких переменных через запятую указываются те из них, по которым берется производная (при этом допускается использование оператора $).

На заметку
Частной производной от функции нескольких переменных называется производная по одной из этих переменных при фиксированных прочих.

При вычислении частных производных допускается также использование оператора D. После оператора в квадратных скобках указывают индекс, соответствующий номеру аргумента функции, по которому вычисляется производная. Например, для функции трех переменных u(x,y,z) производная может быть вычислена с помощью команды D[2,3](u)(x,y,z).

Найти частные производные первого и второго порядков от функции и(х,у) = х’+у*-4х2у2.

Определим функцию двух аргументов (аргументы указываются через запятую и заключаются в скобки).

Используя для записи результата процедуру дифференцирования в неактивной форме (Diff ()), вычислим частную производную по х.

Прочие производные вычисляются аналогично.

Стоит обратить внимание на то, что при вычислении частных производных можно использовать оператор $.

Однако если производных много и они достаточно высокого порядка, запись отдельной команды для каждой такой производной становится утомительным занятием. Иногда в таких случаях полезно определять специальные процедуры, как в следующем примере.

Найти частные производные первого и второго порядков от функции и (х,у) = х».

Как и раньше, определяем функцию.

Однако чтобы не вводить для вычисления производных пять отдельных команд, определим всего одну процедуру, которая будет вычислять все производные вплоть до второго порядка от функции двух неизвестных.

Функция и является параметром процедуры. Первый цикл с оператором do используется для вычисления производных первого порядка. Условие s in x,y указывает на то, что переменная s пробегает значения элементов из последовательности х;у, по которым и берется производная. Так же организован и второй цикл, в котором вычисляются вторые производные, однако он содержит еще один вложенный цикл. В процедуре использована также процедура print(), которая выводит на экран выражение, указанное ее параметром (выражение предварительно вычисляется).

Чтобы отобразить все частные производные функции и, достаточно указать эту функцию в качестве параметра процедуры AllDeriv().

В частности, можно проверить, что смешанные производные не зависят от порядка дифференцирования.

Совет
Как можно видеть, выводимые на экран выражения для частных производных допус-некоторое упрощение. Чтобы это выполнялось автоматически, соответствующую команду (например, simplify()) можно разместить прямо в теле процедуры.

Видео:Простейшие уравнения в частных производныхСкачать

Глава 7

Решение дифференциальных уравнений

Дифференциальные уравнения лежат в основе математического моделирования различных, в том числе физических, систем и устройств [1, 38, 46]. Решению таких уравнений посвящена эта глава. В ней рассмотрено как аналитическое, так и численное решение дифференциальных уравнений различного вида — линейных и нелинейных, классических и специальных, например, в частных производных и с учетом двухсторонних граничных условий. Описание сопровождается множеством наглядных примеров, реализованных в СКМ Maple 9.5/10.

Видео:РЕШЕНИЕ ВОЛНОВОГО ДУ ОПЕРАЦИОННЫМ МЕТОДОМ В СРЕДЕ MAPLESOFT MAPLE 2017Скачать

7.1. Введение в решение дифференциальных уравнений

Видео:Уравнения в частных производных первого порядка| poporyadku.schoolСкачать

7.1.1. Дифференциальные уравнения первого порядка

Дифференциальные уравнения (ДУ) это уравнения, связывающие неизвестную функцию с какими либо ее производными и, возможно, с независимыми переменными. Если неизвестная функция зависит только от одной независимой переменной, то такое уравнение называется обыкновенным дифференциальным уравнением, а если от двух и более многих независимых переменных — дифференциальным уравнением в частных производных.

Простейшее дифференциальное уравнение первого порядка

(7.1)

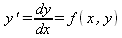
в общем случае имеет множество решений в виде зависимостей y(х). Однако можно получить единственное решение, если задать начальные условия в виде начальных значений х₀ и у₀= у(х₀). Это решение может быть аналитическим, конечно-разностным или численным.

Видео:Уравнения с частными производными 2 ЗадачиСкачать

7.1.2. Решение дифференциального уравнения радиоактивного распада

В качестве примера аналитического решения дифференциального уравнения первого порядка (файл der) запишем дифференциальное уравнение радиоактивного распада атомов (N — число атомов в момент времени t, g=1/c):

Используя функцию dsolve, которая более подробно будет описана чуть позже, получим его общее аналитическое решение:

В решении присутствует произвольная постоянная _С1. Но ее можно заметить на постоянную N(0)=N₀, означающую начальное число атомов в момент t=0:

Если конкретно N₀=100 и g=4, то получим:

Хотя dsolve выдает решение N(t) в символьном виде, оно пока недоступно для построения графика этого решения или просто вычисления в любой точке. Однако, используя функции assign или subs можно сделать это решение доступным. Например, используем такую конструкцию:

Теперь мы можем воспользоваться полученной зависимостью N(t) и построить график ее:

Этот график, который читатель может просмотреть сам, описывает хорошо известным апериодическим экспоненциальный закон уменьшения числа атомов вещества в ходе его радиоактивного распада. Подобные зависимости, кстати, характерны для напряжения на конденсаторе С при его разряде через резистор R, для тока в LA-цепи и для многих простых физических явлений, описывающихся дифференциальным уравнением первого порядка.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

7.1.3. Модели популяций Мальтуса и Ферхюльса-Пирла

Еще одним классическим примером применения дифференциального уравнения первого порядка является давно известная и довольно грубая модель популяции Мальтуса. Не вдаваясь в хорошо известное описание этой модели, отметим, что она описывает численность особей или их биомассу x(t) в любой момент времени (для момента времени х(0)=N) Эта зависимость характеризуется коэффициентами рождаемости α и смертности β. При этом вводится их разность k=α-β.

Представим задание дифференциального уравнения динамики популяций по модели Мальтуса и его решение в аналитическом виде:

dsol1 := x(t) = Ne (k1)

Нетрудно заметить, что решение этого уравнения аналогично решению дифференциального уравнения радиоактивного распада и описывается также экспоненциальной функций. Однако, в зависимости от того, какой фактор (рождаемость или смертность) преобладает наблюдается либо экспоненциальный рост, либо экспоненциальный спад биомассы популяций.

Более правдоподобную модель популяций предложили Ферхюльст и Пирл. Эта модель учитывает (коэффициентом внутривидовую конкуренцию и позволяет учесть приближение популяций к некоторому состоянию равновесия. На рис. 7.1 представлено дифференциальное уравнение динамики популяций Ферхюльста-Пирла. Решения приведены в общем виде, а также для k=g= k/g=1 и разных x(0)=1, 0.5 и 2.

Рис. 7.1. Моделирование популяций по модели Ферхюльста и Пирла

Поведение системы зависит от соотношения k/g и x(0)=N. При их равенстве количество биомассы популяции не меняется. При N>k/g биомасса экспоненциально уменьшается, приближаясь к значению k/g, а при N (n) =f(x, у, у’, y», …, y( n-1) ),

Теперь решение этого уравнения можно свести к решению системы ОДУ:

В таком виде ДУ n-го порядка может решаться стандартными средствами решения систем ОДУ, входящими в большинство математических систем.

Видео:Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

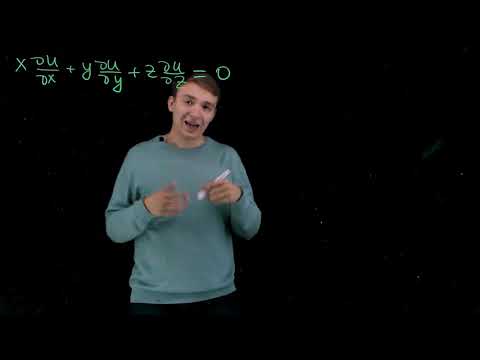
7.1.6. Решение задачи на полет камня

В качестве примера аналитического решения системы дифференциальных уравнений рассмотрим постановку типичной физической задачи моделирования «Бросок камня», позволяющую описать полет камня, брошенного под углом к горизонту.

Модель должна позволять:

Вычислять положение камня в любой момент времени.

Масса камня, начальные координаты, начальная скорость и угол броска мяча.

На основе содержательной модели разрабатывается концептуальная формулировка задачи моделирования. Применительно к нашей задаче движение камня может быть описано в соответствии с законами классической механики Ньютона.

Гипотезы, принятые для модели:

• камень будем считать материальной точкой массой m, положение которой совпадает с центром масс камня;

• движение происходит в поле силы тяжести с постоянным ускорением свободного падения g и описывается уравнениями классической механики Ньютона;

• движение камня происходит в одной плоскости, перпендикулярной поверхность Земли;

• сопротивлением воздуха на первых порах пренебрегаем.

В качестве параметров движения будем использовать координаты (х, у) и скорость v(v_x, v_y) центра масс камня.

Концептуальная постановка задачи на основе принятых гипотез заключается в определении закона движения материальной точки массой m под действием силы тяжести, если известны начальные координаты точки х₀ и ее начальная скорость v₀ и угол броска α₀.

Таким образом, модель является простой — объект, как материальная точка, не имеет внутренней структуры. Учитывая типичные скорости и высоту броска камня, можно считать постоянным ускорение свободного падения. Переход от трехмерных координат к плоскости значительно упрощает решение задачи. Он вполне допустим, если камень не подкручивается при броске. Пренебрежение сопротивлением воздуха, как будет показано далее, приводит к значительной систематической ошибке результатов моделирования.

Теперь перейдем к составлению математической модели объекта — совокупности математических соотношений, описывающих его поведение и свойства. Из законов и определяющих выражений предметной дисциплины формируются уравнения модели.

По оси x на камень не действуют никакие силы, по оси y — действует сила тяжести. Согласно законам Ньютона имеем уравнения движения по оси x и оси y.

(7.2)

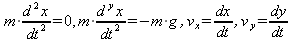
при следующих начальных условиях

Надо найти зависимости x(t), y(y), v_x(r), v_y(t).

Математическая постановка решения задачи в нашем случае соответствует решению задачи Коши для системы обыкновенных дифференциальных уравнений с заданными начальными условиями. Известно, что решение задачи Коши существует и что оно единственное. Количество искомых переменных равно количеству дифференциальных уравнений. Таким образом, математическая модель корректна.

Решение этой задачи есть в любом учебнике физики. Тем не менее, выполним его средствами системы Maple. Из (7.2) запишем систему ОДУ первого порядка:

(7.3)

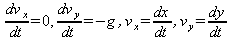
После интегрирования получим:

(7.4)

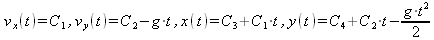
Определив константы интегрирования из начальных условий, окончательно запишем:

Из аналитического решения вытекает, что полет камня при отсутствии сопротивления воздуха происходит строго по параболической траектории, причем она на участках полета камня вверх и вниз симметрична. Необходимые для расчета уравнения заданы в параметрической форме — как зависимости от времени, что, кстати говоря, облегчает моделирование по ним полета камня. Немного позже мы решим эту задачу, используя средства Maple 9.5 для решения систем дифференциальных уравнений.

Видео:Найти общее решение уравнения в частных производных первого порядка.Скачать

7.1.7. Классификация дифференциальных уравнений

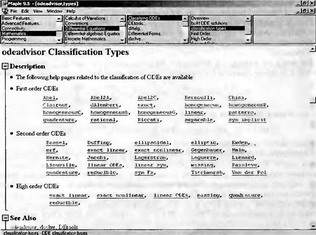
Дифференциальные уравнения могут быть самого разного вида. На рис. 7.2 представлен раздел справки Maple 9.5 с классификацией дифференциальных уравнений. В ней представлено:

• 20 дифференциальных уравнений первого порядка;

• 25 дифференциальных уравнений второго порядка;

• 6 типов дифференциальных уравнений высшего порядка;

• основные функции решения дифференциальных уравнений.

Рис. 7.2. Классификация дифференциальных уравнений

Эта классификация охватывает большую часть классических дифференциальных уравнений, которые используются в математике и в математической физике. Следует отметить, что речь не идет об отдельных функциях по решению таких уравнений частного вида, а о примерах составления соответствующих уравнений и решении их с помощью небольшого числа функций системы Maple 9.5.

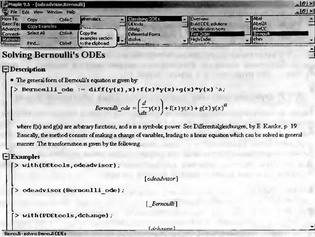
В качестве примера работы с классификатором выберем решение дифференциального уравнения Бернулли. Для этого активизируем на рис. 7.2 гиперссылку с его именем — Bernoulli. Появится окно справки по этому уравнению, показанное на рис. 7.3 с открытой позицией меню Edit.

Рис. 7.3. Окно справки по решению дифференциального уравнения Бернулли

С помощью команды Copy Examples в позиции Edit меню можно перенести примеры решения с окна справки в буфер Clipboard операционной системы Windows. После этого командой Paste в меню Edit окна документа можно перенести примеры в текущий документ — желательно (но не обязательно) новый. Теперь можно наблюдать решение выбранного дифференциального уравнения — рис. 7.4.

Рис. 7.4. Пример решения дифференциального уравнения Бернулли из справки

Возможность выбора и решения с полсотни классических дифференциальных уравнений различного типа дает системе Maple 9.5 преимущества, которые по достоинству оценят пользователи, заинтересованные в знакомстве с такими уравнениями и в их использовании.

В Maple 9.5 средства решения дифференциальных уравнений подверглись значительной переработке. Введены новые методы решения для дифференциальных уравнений Абеля, Риккати и Матье, новые методы инициализации и решения уравнений с кусочными функциями, улучшены алгоритмы решения численными методами. Детальное описание этих новинок можно найти в справке по разделу What’s New…. Это относится и к версии Maple 10.

Видео:6. Линейные однородные уравнения в частных производных первого порядкаСкачать

7.1.8. Функция решения дифференциальных уравнений dsolve

Maple позволяет решать одиночные дифференциальные уравнения и системы дифференциальных уравнений как аналитически, так и в численном виде. Разработчиками системы объявлено о существенном расширении средств решения дифференциальных уравнений и о повышении их надежности в смысле нахождения решений для большинства классов дифференциальных уравнений.

Для решения системы простых дифференциальных уравнений (задача Коши) используется функция dsolve в разных формах записи:

Здесь ODE — одно обыкновенное дифференциальное уравнение или система из дифференциальных уравнений первого порядка с указанием начальных условий, у(х) —функция одной переменной, Ics — выражение, задающее начальные условия, —множество дифференциальных уравнений, — множество неопределенных функций, extra_argument —опция, задающая тип решения.

Параметр extra_argument задает класс решаемых уравнений. Отметим основные значения этого параметра:

• exact — аналитическое решение (принято по умолчанию);

• explicit — решение в явном виде;

• system — решение системы дифференциальных уравнений;

• ICs — решение системы дифференциальных уравнений с заданными начальными условиями;

• formal series — решение в форме степенного многочлена;

• integral transform — решение на основе интегральных преобразований Лапласа, Фурье и др.;

• series — решение в виде ряда с порядком, указываемым значением переменной Order;

• numeric — решение в численном виде.

Возможны и другие опции, подробное описание которых выходит за рамки данной книги. Его можно найти в справке по этой функции, вызываемой командой ?dsolve.

Для решения задачи Коши в параметры dsolve надо включать начальные условия, а при решении краевых задач — краевые условия. Если Maple способна найти решение при числе начальных или краевых условий меньше порядка системы, то в решении будут появляться неопределенные константы вида _С1, _С2 и т.д. Они же могут быть при аналитическом решении системы, когда начальные условия не заданы. Если решение найдено в неявном виде, то в нем появится параметр _Т. По умолчанию функция dsolve автоматически выбирает наиболее подходящий метод решения дифференциальных уравнений. Однако в параметрах функции dsolve в квадратных скобках можно указать предпочтительный метод решения дифференциальных уравнений. Допустимы следующие методы:

[quadrature, linear, Bernoulli, separable, inverse_linear, homogeneous, Chini, lin_sym, exact, Abel, pot_sym ]

Более полную информацию о каждом методе можно получить, используя команду ?dsolve,method и указав в ней конкретный метод. Например, команда ?dsolve,linear вызовет появление страницы справочной системы с подробным описанием линейного метода решения дифференциальных уравнений.

Видео:Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

7.1.9. Уровни решения дифференциальных уравнений

Решение дифференциальных уравнений может сопровождаться различными комментариями. Команда

где n — целое число от 0 до 5 управляет уровнями детальности вывода. По умолчанию задано n = 0. Значение n = 5 дает максимально детальный вывод.

Производные при записи дифференциальных уравнений могут задаваться функцией diff или оператором дифференцирования D. Выражение sysODE должно иметь структуру множества и содержать помимо самой системы уравнений их начальные условия.

Читателю, всерьез интересующемуся проблематикой решения линейных дифференциальных уравнений, стоит внимательно просмотреть разделы справки по ним и ознакомиться с демонстрационным файлом linearoade.mws, содержащим примеры решения таких уравнений в закрытой форме.

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

7.2. Примеры решения дифференциальных уравнений

Видео:Уравнения в частных производных 1Скачать

7.2.1. Примеры аналитического решение ОДУ первого порядка

Отвлекшись от физики, приведем несколько примеров на составление и решение дифференциальных уравнений первого порядка в аналитическом виде (файл dea):

ln(sin(x)) — ln(у(x)) + _C1 = 0

Разумеется, приведенными примерами далеко не исчерпываются возможности аналитического решения дифференциальных уравнений.

Видео:Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

7.2.2. Полет тела, брошенного вверх

Из приведенных выше примеров видно, что для задания производной используется ранее рассмотренная функция diff. С помощью символа $ в ней можно задать производную более высокого порядка.

В соответствии со вторым законом Ньютона многие физические явления, связанные с движением объектов, описываются дифференциальными уравнениями второго порядка. Ниже дан пример задания и решения такого уравнения (файл

dem), описывающего движение тела, брошенного вверх на высоте h₀ со скоростью v₀ при ускорении свободного падения g:

Итак, получено общее уравнение для временной зависимости высоты тела h(t). Разумеется, ее можно конкретизировать, например, для случая, когда g=9,8, h₀=10 и v₀=100:

Зависимость высоты тела от времени h(t) представлена на рис. 7.5. Нетрудно заметить, что высота полета тела вначале растет и достигнув максимума начинает снижаться. Оговоримся, что сопротивление воздуха в данном примере не учитывается, что позволяет считать задачу линейной. Полученное с помощью Maple 9.5 для этого случая решение совпадает с полученным вручную в примере, описанном в разделе 7.1.3.

Рис. 7.5. Зависимость высоты полета тела от времени h(t)

Видео:Горицкий А. Ю. - Уравнения математической физики - Уравнения с частными производными 1-го порядкаСкачать

7.2.3. Поведение идеального гармонического осциллятора

Еще одним классическим применением дифференциальных уравнений второго порядка является решение уравнение идеального гармонического осциллятора (файл deio):

у(t) = _C1 sin(ω) + _C2 cos(ω)

График решения этого уравнения (рис. 7.6) представляет хорошо известную синусоидальную функцию. Интересно, что амплитуда колебаний в общем случае отлична от 1 и зависит от значения у(0) — при у(0)=0 она равна 1 (в нашем случае синусоида начинается со значение у(0)=-1). Подобным осциллятором может быть LC-контур или механический маятник без потерь.

Рис. 7.6. Решение дифференциального уравнения идеального осциллятора

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

7.2.4. Дополнительные примеры решения дифференциальных уравнений второго порядка

Ниже представлено решение еще двух дифференциальных уравнений второго порядка в аналитическом виде (de2a):

у(x) = -½sin(x) + ½cos(x) + e x _C1 + _C2

Ряд примеров на применение дифференциальных уравнений второго порядка при решении практических математических и физических задач вы найдете в главе 11.

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

7.2.5. Решение систем дифференциальных уравнений

Функция dsolve позволяет также решать системы дифференциальных уравнений. Для этого она записывается в виде

dsolve(ODE_sys, optional_1, optional_2. )

Здесь ODE_sys — список дифференциальных уравнений, образующих систему, остальные параметры опциональные и задаются по мере необходимости. Они могут задавать начальные условия, явно представлять искомые зависимости, выбирать метод решения и т.д. Детали задания опциональных параметров можно найти в справке.

На рис. 7.7 представлено решение системы из двух дифференциальных уравнений различными методами — в явном виде, в виде разложения в ряд и с использованием преобразования Лапласа. Здесь следует отметить, что решение в виде ряда является приближенным. Поэтому полученные в данном случае аналитические выражения отличаются от явного решения и решения с применением преобразования Лапласа.

Рис. 7.7. Решение системы из двух дифференциальных уравнений различными методами

Следует отметить, что, несмотря на обширные возможности Maple в области аналитического решения дифференциальных уравнений, оно возможно далеко не всегда. Поэтому, если не удается получить такое решение, полезно попытаться найти решение в численном виде. Практически полезные примеры решения дифференциальных уравнений, в том числе с постоянными граничными условиями, вы найдете в Главе 11.

7.2.6. Модель Стритера-Фелпса для динамики кислорода в воде

В качестве еще одного примера решении системы из двух дифференциальных уравнений рассмотрим модель Стритера-Фелпса, предложенную для описания динамики содержания растворенного в воде кислорода. Описание этой модели можно найти в [41]. Ниже представлено задание этой модели в виде системы из двух дифференциальных уравнений и их аналитическое решение (файл demp):

Здесь: x1(t) — концентрация в воде растворенного кислорода в момент времени t; x2(t) — концентрация биохимического потребления кислорода (БПК), С — концентрация насыщения воды кислородом, K1 — постоянная скорости аэрации, K2 — постоянная скорости уменьшения (БПК), a — начальное значение x1(t) и b — начальное значение х2(t) при t=0.

В данном случае получены два варианта аналитического решения — основное и упрощенное с помощью функции simplify. Читатель может самостоятельно построить графики зависимостей x1(t) и x2(t).

7.3. Специальные средства решения дифференциальных уравнений

7.3.1. Численное решение дифференциальных уравнений

К сожалению, аналитического решения в общем случае нелинейные дифференциальные уравнения не имеют. Поэтому их приходится решать численными методами. Они удобны и в том случае, когда решение надо представить числами или, к примеру, построить график решения. Поясним принципы численного решения.

Для этого вернемся к дифференциальному уравнению (7.1). Заменим приращение dx на малое, но конечное приращение dx=h. Тогда приращение dy будет равно

Если, к примеру, известно начальное значение у=у₀, то новое значение у будет равно

Распространяя этот подход на последующие шаги решения получим конечно-разностную формулу для решение приведенного уравнения в виде:

Эта формула известна как формула простого метода Эйлера первого порядка для решения дифференциального уравнения (7.1). Можно предположить (так оно и есть), что столь простой подход дает большую ошибку — отбрасываемый член порядка O(h 2 ). Тем не менее, физическая и математическая прозрачность данного метода привела к тому, что он широко применяется на практике.

Существует множество более совершенных методов решения дифференциальных уравнений, например, усовершенствованный метод Эйлера, метод трапеций, метод Рунге-Кутта, метод Рунге-Кутта-Фельберга и др. Ряд таких методов реализован в системе Maple и может использоваться при численном решении дифференциальных уравнений и систем с ними.

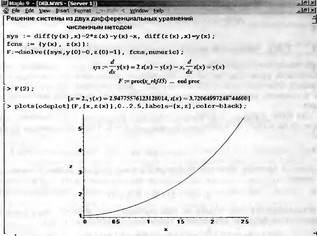
Для решения дифференциальных уравнений в численном виде в Maple используется та же функция dsolve с параметром numeric или type=numeric. При этом решение возвращается в виде специальной процедуры, по умолчанию реализующей широко известный метод решения дифференциальных уравнений Рунге-Кутта-Фельберга порядков 4 и 5 (в зависимости от условий адаптации решения к скорости его изменения). Эта процедура называется rkf45 и символически выводится (без тела) при попытке решения заданной системы дифференциальных уравнений. Последнее достаточно наглядно иллюстрирует рис. 7.8.

Рис. 7.8. Решение системы дифференциальных уравнений численным методом rkf45 с выводом графика решения

Указанная процедура возвращает особый тип данных, позволяющих найти решение в любой точке или построить график решения (или решений). Для графического отображения Maple 9.5 предлагает ряд возможностей и одна из них представлена на рис. 7.8 — см. последнюю строку ввода. При этом используется функция plot[odeplot] из пакета odeplot, предназначенного для визуализации решений дифференциальных уравнений. Можно воспользоваться и функцией plot, выделив тем или иным способом (примеры уже приводились) нужное решение.

В список параметров функции dsolve можно явным образом включить указание на метод решения, например опция method=dverk78 задает решение непрерывным методом Рунге-Кутта порядка 7 или 8. Вообще говоря, численное решение дифференциальных уравнений можно производить одним из следующих методов:

• classical — одна из восьми версий классического метода, используемого по умолчанию;

• rkf45 — метод Рунге-Кутта 4 или 5 порядка, модифицированный Фелбергом;

• dverk78 — непрерывный метод Рунге-Кутта порядка 7 или 8;

• gear — одна из двух версий одношагового экстраполяционного метода Гира;

• mgear — одна из трех версий многошагового экстраполяционного метода Гира;

• lsode — одна из восьми версий Ливенморского решателя жестких дифференциальных уравнений;

• taylorseries — метод разложения в ряд Тейлора.

Обилие используемых методов расширяет возможности решения дифференциальных уравнений в численном виде. Большинство пользователей Maple вполне устроит автоматический выбор метода решения по умолчанию. Однако в сложных случаях, или когда заведомо желателен тот или иной конкретный алгоритм численного решения, возможна прямая установка одного из указанных выше методов.

С помощью параметра ‘abserr’=aerr можно задать величину абсолютной погрешности решения, а с помощью ‘minerr’=mine — минимальную величину погрешности. В большинстве случаев эти величины, заданные по умолчанию, оказываются приемлемыми для расчетов.

Maple реализует адаптируемые к ходу решения методы, при которых шаг решения h автоматически меняется, подстраиваясь под условия решения. Так, если прогнозируемая погрешность решения становится больше заданной, шаг решения автоматически уменьшается. Более того, система Maple способна автоматически выбирать наиболее подходящий для решаемой задачи метод решения.

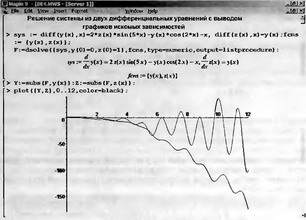
Еще один пример решения системы дифференциальных уравнений представлен на рис. 7.9. Здесь на одном графике представлены зависимости y(x) и z(x) представляющие полное решение заданной системы. При этом процедура имеет особый вид listprocedure и для преобразования списка выходных данных в векторы решения Y и Z используется функция subs.

Рис. 7.9. Решение системы дифференциальных уравнений численным методом с выводом всех графиков искомых зависимостей

Для решения достаточно сложных задач полезны специальная структура DESol для решения дифференциальных уравнений и инструментальный пакет SEtools, содержащий самые изысканные средства для графической визуализации результатов решения дифференциальных уравнений. Эти средства мы более подробно рассмотрим в дальнейшем.

При решении некоторых задач физики и радиоэлектроники выбираемый по умолчанию шаг изменения аргумента х или t-h может привести к неустойчивости решения. Неустойчивости можно избежать рядом способов. Можно, например, нормировать уравнения, избегая необходимости использования малого шага. А можно задать заведомо малый шаг. Например, при method=classical для этого служит параметр stepsize=h.

7.3.2. Дифференциальные уравнения с кусочными функциями

Состоящие из ряда кусков кусочные функции широко используются при математическом моделировании различных физических объектов и систем. В основе такого моделирования обычно лежит решение дифференциальных уравнений, описывающих поведение объектов и систем. Покажем возможность применения кусочных функций для решения дифференциальных уравнений.

Ниже представлено задание дифференциального уравнения первого порядка, содержащего кусочную функцию:

Нетрудно заметить, что результат получен также в форме кусочной функции, полностью определяющей решение на трех интервалах изменения х.

Приведем пример решения дифференциального уравнения второго порядка с кусочной функцией:

> eq := diff(y(х), х$2) + x*diff(y(x), х) + y(х) = piecewise(х > 0, 1);

В заключении этого раздела приведем пример решения нелинейного дифференциального уравнения Риккати с кусочной функцией:

В ряде случаев желательна проверка решения дифференциальных уравнений. Ниже показано, как она делается для последнего уравнения:

Как видно из приведенных достаточно простых и наглядных примеров, результаты решения дифференциальных уравнений с кусочными функциями могут быть довольно громоздкими. Это, однако, не мешает эффективному применению функций этого класса.

7.3.3. Структура неявного представления дифференциальных уравнений — DESol

В ряде случаев иметь явное представление дифференциальных уравнений нецелесообразно. Для неявного их представления в Maple введена специальная структура

где exprs — выражение для исходной системы дифференциальных уравнений, vars — заданный в виде опции список переменных (или одна переменная).

Структура DESol образует некоторый объект, дающий представление о дифференциальных уравнениях, чем-то напоминающее RootOf. С этим объектом можно обращаться как с функцией, то есть его можно интегрировать, дифференцировать, получать разложение в ряд и вычислять численными методами.

На рис. 7.10 показаны примеры применения структуры DESol.

Рис. 7.10. Примеры применения структуры DESol

Обратите внимание на последний пример — в нем структура DESol использована для получения решения дифференциального уравнения в виде степенного ряда.

7.4. Инструментальный пакет решения дифференциальных уравнений DEtools

7.4.1. Средства пакета DEtools

Решение дифференциальных уравнений самых различных типов — одно из достоинств системы Maple. Пакет DEtools предоставляет ряд полезных функций для решения дифференциальных уравнений и систем с такими уравнениями. Для загрузки пакета используется команда:

Этот пакет дает самые изысканные средства для аналитического и численного решения дифференциальных уравнений и систем с ними. По сравнению с версией Maple V R5 число функций данного пакета в Maple 9.5 возросло в несколько раз. Многие графические функции пакета DEtools были уже описаны. Ниже приводятся полные наименования тех функций, которые есть во всех реализациях системы Maple:

• DEnormal — возвращает нормализованную форму дифференциальных уравнений;

• DEplot — строит графики решения дифференциальных уравнений;

• DEplot3d — строит трехмерные графики для решения систем дифференциальных уравнений;

• Dchangevar — изменение переменных в дифференциальных уравнениях;

• PDEchangecoords — изменение координатных систем для дифференциальных уравнений в частных производных;

• PDEplot — построение графиков решения дифференциальных уравнений в частных производных;

• autonomous — тестирует дифференциальные уравнения на автономность;

• convertAlg — возвращает список коэффициентов для дифференциальных уравнений;

• convertsys — преобразует систему дифференциальных уравнений в систему одиночных уравнений;

• dfieldplot — строит график решения дифференциальных уравнений в виде векторного поля;

• indicialeq — преобразует дифференциальные уравнения в полиномиальные;

• phaseportrait — строит график решения дифференциальных уравнений в форме фазового портрета;

• reduceOrder — понижает порядок дифференциальных уравнений;

• regularsp — вычисляет регулярные особые точки для дифференциальных уравнений второго порядка;

• translate — преобразует дифференциальные уравнения в список операторов;

• untranslate — преобразует список операторов в дифференциальные уравнения;

• varparam — находит общее решение дифференциальных уравнений методом вариации параметров.

Применение этих функций гарантирует совместимость документов реализаций Maple R5, 6 и 9.

7.4.2. Консультант по дифференциальным уравнениям

Для выявления свойств дифференциальных уравнений в Maple 9.5 в составе пакета DEtools имеется консультант (адвизор), вводимый следующей функцией:

odeadvisor(ODE) odeadvisor(ODE, y(х), [type1, type2. ], help)

Здесь ODE — одиночное дифференциальное уравнение, y(x) — неопределенная (определяемая функция), type1, type2, … — опционально заданные множество типов, которые классифицируются и help — опционально заданное указание на вывод страницы справки по методу решения.

Примеры работы с классификатором представлены ниже: