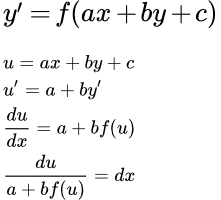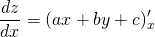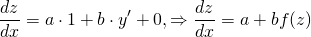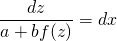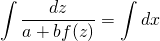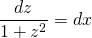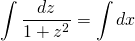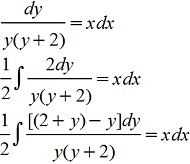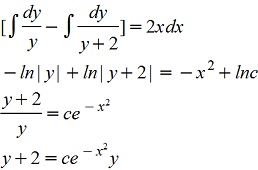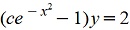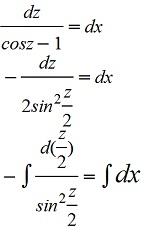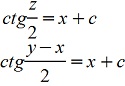Дифференциальные уравнения ax by c

Видео:Дифференциальные уравнения. 11 класс.Скачать

Постановка задачи

Рассмотрим дифференциальное уравнение
(i) ,
где f – функция, a, b, c – постоянные, b ≠ 0 .
Это уравнение приводится к уравнению с разделяющимися переменными.

Видео:2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Метод решения

Делаем подстановку:
u = ax + by + c
Здесь y – функция от переменной x . Поэтому u – тоже функция от переменной x .
Дифференцируем по x
u′ = ( ax + by + c )′ = a + by′
Подставляем (i)
u′ = a + by′ = a +b f ( ax + by + c ) = a + b f ( u )
Или:
(ii)
Разделяем переменные. Умножаем на dx и делим на a + b f ( u ) . Если a + b f ( u ) ≠ 0 , то

Интегрируя, мы получаем общий интеграл исходного уравнения (i) в квадратурах:
(iii) .

В заключении рассмотрим случай
(iv) a + b f ( u ) = 0 .
Предположим, что это уравнение имеет n корней u = r_i , a + b f ( r_i ) = 0 , i = 1, 2, . n . Поскольку функция u = r_i является постоянной, то ее производная по x равна нулю. Поэтому u = r_i является решением уравнения (ii).
Однако, уравнение (ii) не совпадает с исходным уравнением (i) и, возможно, не все решения u = r_i , выраженные через переменные x и y , удовлетворяют исходному уравнению (i).

Таким образом, решением исходного уравнения является общий интеграл (iii) и некоторые корни уравнения (iv).

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Пример решения дифференциального уравнения, приводящегося к уравнению с разделяющимися переменными

Решить уравнение
(1)

Делаем подстановку:
u = x – y
Дифференцируем по x и выполняем преобразования:
;

Умножаем на dx и делим на u 2 .

Если u ≠ 0 , то получаем:

Интегрируем:

Применяем формулу из таблицы интегралов:

Вычисляем интеграл

Тогда
;
, или

Общее решение:
.

Теперь рассмотрим случай u = 0 , или u = x – y = 0 , или
y = x .
Поскольку y′ = ( x )′ = 1 , то y = x является решением исходного уравнения (1).

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 16-07-2012 Изменено: 22-02-2015

Видео:1. Что такое дифференциальное уравнение?Скачать

Как решать уравнения, приводимые к уравнениям с разделяющимися переменными

Рассмотрим, как решать уравнения вида y’=f(ax+by+c), где a,b,c — некоторые числа. Это — дифференциальные уравнения, приводимые к уравнениям с разделяющимися переменными.

Такие уравнения приводятся к уравнениям с разделяющимися переменными с помощью замены z=ax+by+c. Дифференцируем обе части этого равенства по иксу:

Поскольку x’=1, а так как y’=f(ax+by+c), то y’=f(z).

Соответственно, получаем, что

При условии a+bf(z)≠0 переменные можем разделить:

Интегрируем полученное уравнение

В полученном решении возвращаемся к исходным переменным z=ax+by+c.

Если a+bf(z)=0, то значит, и dz/dx=0, то ax+by+c=С.

Решить уравнение y’=(x+y+1)².

Решение: Замена z=x+y+1. Тогда dz/dx=1+dy/dx, а так как dy/dx=y’=(x+y+1)²=z², то dz/dx=1+z². Разделяем переменные, для этого обе части делим на 1+z² (это выражение не равно нулю при любом z) и умножаем на dx:

arctgz=x+C. Так как z=x+y+1, то общее решение arctg(x+y+1)=x+C, откуда arctg(x+y+1)-x=C.

Видео:Дифференциальные уравнения с разделяющими переменными. 11 класс.Скачать

Примеры решений дифференциальных уравнений с разделяющимися переменными (и сводящихся к ним)

Примеры решений дифференциальных уравнений с разделяющимися переменными (и сводящихся к ним)

1.Общий вид y’=f(x)*g(y), х∈ (a,b)

m(x)*n(y)dy+p(x)*q(y)dx=0, х∈ (a,b)

Для решения такого уравнения, надо обе части умножить или разделить на такое выражение чтобы в одну часть уравнения входил только х, в другую только y, а затем проинтегрировать обе части.

При этом при делении могут быть потряны решения.

Пример:

y’-xy 2 =2xy

y’=xy(y+2)

Делим на y(y+2)

При делении на y(y+2) потеряно решение у=0

2) Уравнение вида y’=f(ax+by) приводятся к уравнениям с разделяющимися переменными заменой z=ax+by или z=ax+by+c где с любая

Пример.

y’=cos(y-x)

замена z(x)=y(x)-x

y’=z’+1

z’+1=cosz

При делении на (cosz-1) потеряли решение cosz-1=0; z=2πk, k∈ z. y-x= 2πk

💡 Видео

Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

Дифференциальные уравнения, 6 урок, Уравнения в полных дифференциалахСкачать

Общее и частное решение дифференциального уравненияСкачать

Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

Дифференциальные уравнения с разделенными переменными. 11 класс.Скачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Линейное неоднородное дифференциальное уравнение 2 способаСкачать