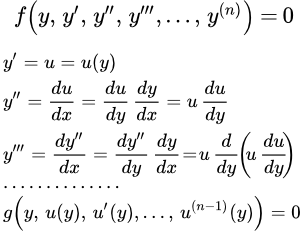Дифференциальное уравнение явно не содержащее переменную

Видео:14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Метод решения

Рассмотрим уравнение, не содержащее независимую переменную в явном виде:
(1) .
Порядок этого уравнения понижается на единицу с помощью подстановки:

Далее считаем, что функция u зависит от переменной y , тогда:
;
;
и т. д.

В результате такой подстановки, порядок уравнения понижается на единицу.

Видео:Дифференциальные уравнения, не содержащие явно независимой переменной (часть 1). Высшая математика.Скачать

Пример

Уравнение не содержит независимую переменную в явном виде. Делаем подстановку:
.
Считаем, что функция u зависит от переменной y . Тогда
.

Подставляем в исходное уравнение:
.
Делим на u . При имеем:
.
Это уравнение с разделяющимися переменными. Делим на и умножаем на dy . При имеем:
.
Интегрируем:
(2) .

Подставляем в (2):
.
Потенцируем:
.
Заменим постоянную интегрирования . Знак модуля сводится к умножению на ±1 . Включим ±1 в постоянную . То есть мы теперь полагаем, что может быть не только положительным, но и отрицательным числом. Тогда:
.

Выполняем преобразования:
;
.
При имеем:
;
.

Разделяем переменные:
.
Интегрируем:
(3) .

Вычисляем интеграл:

.
Подставляем в (3):
;
.
Возводим в квадрат и выполняем преобразования:
;
;
(4) .

При выводе формулы (4) мы предполагали, что
и .
Теперь рассмотрим случаи
.
Нетрудно видеть, что решение, охватывающее эти три равенства, есть
(5) ,
где C – произвольная постоянная. Тогда . Подставляя это в исходное уравнение нетрудно убедиться, что оно выполняется. Это особое решение. Добавим его в ответ.

Автор: Олег Одинцов . Опубликовано: 18-07-2013 Изменено: 27-06-2018

Видео:ДУ высших порядков, не содержащие независимую переменную.Скачать

Дифференциальные уравнения, допускающие понижение порядка

Рассмотрим три частных случая решения дифференциальных уравнений с возможностью понижения порядка. Во всех случаях понижение порядка производится с помощью замены переменной. То есть, решение дифференциального уравнения сводится к решению уравнения более низкого порядка. В основном мы рассмотрим способы понижения порядка дифференциальных уравнений второго порядка, однако их можно применять многократно и понижать порядок уравнений изначально более высокого порядка. Так, в примере 2 решается задача понижения порядка дифференциального уравнения третьего порядка.

Видео:Дифференциальные уравнения, не содержащие явно независимой переменной (часть 2). Высшая математика.Скачать

Понижение порядка уравнения, не содержащего y и y‘

Это дифференциальное уравнение вида . Произведём замену переменной: введём новую функцию и тогда . Следовательно, и исходное уравнение превращается в уравнениие первого порядка

с искомой функцией .

Решая его, находим . Так как , то .

Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:

,

где и — произвольные константы интегрирования.

Пример 1. Найти общее решение дифференциального уравнения

.

Решение. Произведём замену переменной, как было описано выше: введём функцию и, таким образом, понизив порядок уравнения, получим уравнение первого порядка . Интегрируя его, находим . Заменяя на и интегрируя ещё раз, находим общее решение исходного дифференциального уравнения:

Пример 2. Решить дифференциальное уравнение третьего порядка

.

Решение. Дифференциальное уравнение не содержит y и y‘ в явном виде. Для понижения порядка применяем подстановку:

.

Тогда и получаем линейное дифференциальное уравнение первого порядка:

.

Заменяя z произведением функций u и v , получим

Тогда получим выражения с функцией v :

Выражения с функцией u :

Дважды интегрируем и получаем:

.

.

Интегрируем по частям и получаем:

.

Итак, общее решение данного дифференциального уравения:

.

Видео:Дифференциальные уравнения, не содержащие явно независимой переменной (часть 3). Высшая математика.Скачать

Понижение порядка уравнения, не содержащего y

Это дифференциальное уравнение вида . Произведём замену переменной как в предыдущем случае: введём , тогда , и уравнение преобразуется в уравнение первого порядка . Решая его, найдём . Так как , то . Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:

,

где и — произвольные константы интегрирования.

Пример 3. Найти общее решение дифференциального уравнения

.

Решение. Уже знакомым способом произведём замену переменной: введём функцию и понизим порядок уравнения. Получаем уравнение первого порядка . Решая его, находим . Тогда и получаем решение исходного дифференциального уравнения второго порядка:

.

Пример 4. Решить дифференциальное уравнение

.

Решение. Дифференциальное уравнение не содержит y в явном виде. Поэтому для понижения порядка применяем подстановку:

.

Получим дифференциальное уравнение первого порядка:

.

Это уравение с разделяющимися переменными. Решим его:

Интегрируем полученную функцию:

Мы пришли к цели — общему решению данного дифференциального уравения:

.

Пример 5. Найти общее решение дифференциального уравнения

.

Решение. Дифференциальное уравнение не содержит y в явном виде. Поэтому для понижения порядка применяем подстановку:

.

Получим дифференциальное уравнение первого порядка:

.

Это однородное уравение, которое решается при помощи подстановки . Тогда , :

Далее потребуется интегрировать по частям. Введём обозначения:

Таким образом, получили общее решение данного дифференциального уравения:

.

Видео:Дифференциальные уравнения, не содержащие явно искомой функции (часть 2). Высшая математика.Скачать

Понижение порядка уравнения, не содержащего x

Это уравнение вида . Вводим новую функцию , полагая . Тогда

.

Подставляя в уравнение выражения для и , понижаем порядок уравнения. Получаем уравнение первого порядка относительно z как функции от y:

.

Решая его, найдём . Так как , то . Получено дифференциальное уравнение с разделяющимися переменными, из которого находим общее решение исходного уравнения:

,

где и — произвольные константы интегрирования.

Пример 6. Найти общее решение дифференциального уравнения

.

Решение. Полагая и учитывая, что , получаем . Понизив порядок исходного уравнения, получаем уравнение первого порядка с разделяющимися переменными. Приводя его к виду и интегрируя, получаем , откуда . Учитывая, что , находим , откуда получаем решение исходного дифференциального уравнения второго порядка:

.

При сокращении на z было потеряно решение уравнения , т.е. . В данном случае оно содержится в общем решении, так как получается из него при (за исключением решения y = 0).

Пример 7. Найти общее решение дифференциального уравнения

.

Решение. Дифференциальное уравнение не содержит x в явном виде. Для понижения порядка применяем подстановку:

.

Получим дифференциальное уравнение первого порядка:

.

Это уравение с разделяющимися переменными. Решим его:

Используя вновь подстановку

,

получим ещё одно уравнение с разделяющимися переменными. Решим и его:

Таким образом, общее решение данного дифференциального уравения:

.

Пример 8. Найти частное решение дифференциального уравнения

,

удовлетворяющее начальному условию y(0) = 1 , y‘(0) = −1 .

Решение. Дифференциальное уравнение не содержит x в явном виде. Поэтому применяем подстановку:

.

Таким образом, понизили порядок уравнения и получили уравнение первого порядка

.

Это дифференциальное уравнение с разделяющимися переменными. Разделяем переменные и интегрируем:

Чтобы определить C 1 , используем данные условия y(0) = 1 , y‘(0) = −1 или p(0) = −1 . В полученное выражение подставим y = 1 , p = −1 :

.

.

Разделяя переменные и интегрируя, получаем

.

Из начального условия y(0) = 1 следует

.

Получаем окончательное решение данного дифференциального уравнения

.

Пример 9. Найти частное решение дифференциального уравнения

,

удовлетворяющее начальному условию y(1) = 1 , y‘(1) = −1 .

Решение. Дифференциальное уравнение не содержит x в явном виде. Для понижения порядка применяем подстановку:

.

Таким образом, получили уравнение первого порядка

.

Это дифференциальное уравнение с разделяющимися переменными. Разделив обе части уравнения на p , получим

Интегрируем обе части уравнения

Используем начальные условия и определим C 1 . Если x = 1 , то y = 1 и p = y‘ = −1 , поэтому

.

Из начального условия y(1) = 1 следует

.

Получаем окончательное решение данного дифференциального уравнения

.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения, допускающие понижение порядка — ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

8.6. Дифференциальные уравнения, допускающие понижение порядка

В дальнейшем, рассматривая дифференциальные уравнения высших порядков, ограничимся уравнениями второго порядка в силу того, что чаще всего на практике встречаются именно дифференциальные уравнения второго порядка.

1. Уравнение, не содержащее явно неизвестной функции y(х):

Для понижения порядка данного уравнения введем новую неизвестную функцию z(x) = у’(х). В результате исходное дифференциальное уравнение примет вид F(x, z, z’) = 0, решая которое найдем z = φ(x, C1) .

Учитывая, что у'(х) = z(x) = φ(х, C1), получим

Пример. Найдем общее решение дифференциального уравнения х ∙ у» = у’.

Сделав замену неизвестной функции z(x) = у'(х), получим уравнение x ∙ z’ = z, которое является уравнением с разделяющимися переменными:

2. Уравнение, не содержащее независимой переменной х:

Введем новую неизвестную функцию р(у(х)) = у’ и примем у за независимую переменную. Тогда у’’ = р’ ∙ у’ = р’ ∙ р и исходное дифференциальное уравнение будет иметь вид F(y, р, р’ ∙ р) = 0, которое является уравнением первого порядка относительно неизвестной функции р(у). Определив общее решение данного уравнения р = р(у, С1), получим дифференциальное уравнение для определения у: dy/dx = р(у, С1). Это дифференциальное уравнение с разделяющимися переменными, метод решения которого был рассмотрен выше:

Проинтегрировав последнее соотношение, получим общее решение исходного дифференциального уравнения:

Пример. уу’’ –у’2 = 0. Введем новую неизвестную функцию р(у(х)) = у’ и, учитывая, что у’’ = р’ ∙ р, преобразуем дифференциальное уравнение к виду ур’р — р2 = 0. Далее имеем р(ур’ — р) = 0, из чего следует два уравнения р = 0 или ур’ — р = 0.

Первое уравнение при переходе к исходной неизвестной функции принимает вид у’ = 0, которое имеет решение у = С. Это особое решение исходного уравнения.

Второе уравнение является дифференциальным уравнением с разделяющимися переменными:

Далее, возвращаясь к исходной неизвестной функции, получим дифференциальное уравнение dy/dx = C1y, которое тоже является уравнением с разделяющимися переменными:

Вводя новую произвольную постоянную получим окончательный вид общего решения исходного дифференциального уравнения:

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

© 2014-2022 Все права на дизайн сайта принадлежат С.Є.А.

🎬 Видео

Диффуры, не содержащие искомую функцию yСкачать

Дифференциальные уравнения, не содержащие явно искомой функции (часть 1). Высшая математика.Скачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Дифференциальные уравнения, не содержащие явно искомой функции (часть 3). Высшая математика.Скачать

Дифференциальные уравнения, 7 урок, Дифференциальные уравнения, допускающие понижение порядкаСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

ДУ высших порядков, не содержащие независимую переменную. ПримерыСкачать

Дифференциальные уравнения высших порядков, допускающие понижение порядкаСкачать

ДУ Уравнения, не разрешенные относительно производнойСкачать

Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать

Понижение порядка ДУ не содержащего X. Задача о математическом маятнике | Дифференциальные уравненияСкачать

Дифференциальные уравнения. 11 класс.Скачать