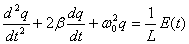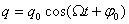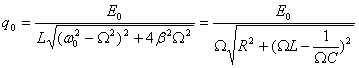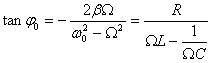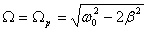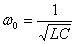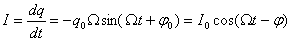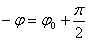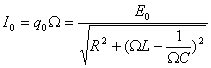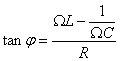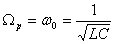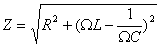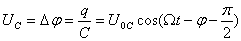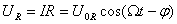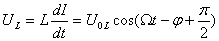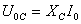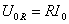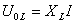Дифференциальное уравнение вынужденных электрических колебаний (3 видео)

Содержание

Вынужденные колебания
Определение вынужденных колебаний
Дифференциальное уравнение вынужденных колебаний
Резонанс вынужденных колебаний
Примеры задач с решением
Вынужденные электрические колебания
Вынужденные колебания. Переменный ток
Что такое переменный ток?
Цепи переменного тока
Векторная диаграмма токов и напряжений
Резистор в цепи переменного тока
Конденсатор в цепи переменного тока
🔥 Видео

Видео:Вынужденные электромагнитные колебания. Автоколебания. 11 класс.Скачать

Вынужденные колебания

Видео:71. Вынужденные колебанияСкачать

Определение вынужденных колебаний

Для того чтобы в реально существующей колебательной системе получать незатухающие колебания, следует каким-либо образом компенсировать потери энергии, которые происходят в результате существования сил сопротивления. Самым простым способом реализации незатухающих колебаний является воздействие на систему при помощи внешней периодической силы. Работа внешней силы обеспечить приток энергии в систему извне. Эта энергия не даст колебаниям затухнуть, при действии сил трения.

Колебания, которые возникают под действием периодически меняющейся силы (периодически изменяющейся ЭДС), называют вынужденными механическими (электромагнитными) колебаниями.

Видео:Урок 347. Вынужденные колебания. Резонанс (часть 1)Скачать

Дифференциальное уравнение вынужденных колебаний

Допустим, на механическую колебательную систему действует гармонически изменяющаяся внешняя сила:

Рассмотрим колебания груза на пружине (пружинный маятник). Уравнение незатухающих гармонических колебаний для этой системы можно записать как:

где $x$ — координата; $delta $ — коэффициент затухания; $_0$ — циклическая частота свободных незатухающих колебаний (если $delta $=0, то $_$называют собственной частотой колебаний).

Если рассматривается, например, электрический колебательный контур, то роль периодически действующей силы может играть внешняя ЭДС или переменное напряжение. Их подводят к контуру извне и изменяются они по гармоническому закону. Уравнение колебаний в электрическом контуре можно представить как:

где $q$ — заряд; $delta =frac$ — коэффициент затухания; $_0=frac<sqrt>$; $U=U_m$ — внешнее переменное напряжение.

Уравнения (2) и (3) можно свести к линейному неоднородному дифференциальному уравнению вида:

где $s$ — колеблющийся параметр; $x_0=frac$ если колебания механические ($x_0=frac— в случае электрических колебаний$).

Решением уравнения (4) является сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение при этом имеет вид:

Его общее решение:

где $A_0$ — начальная амплитуда колебаний.

Частное решение уравнения (4) в представлено выражением:

Слагаемое $s_1$ в решении уравнения (5) играет значительную роль в начальной стадии установления колебаний, пока амплитуда вынужденных колебаний не будет определяться выражением (8).

Установившись, вынужденные колебания происходят с частотой $omega $ и являются гармоническими. Амплитуда и фаза этих колебаний определяются равенствами (8) и (9), и они зависят от частоты $omega $.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Резонанс вынужденных колебаний

Если частота вынуждающей силы приближается к собственной частоте колебаний, то возникает резкое увеличение амплитуды колебаний. Такое явление называют резонансом.

Из выражения (8) видно, что амплитуда имеет максимум. Для нахождения резонансной частоты (частоты при которой $A=max$), следует найти максимум функции $A(omega )$. Взяв производную $frac$ и приравняв ее к нулю получим:

Равенство (10) справедливо при:

Получается, что резонансная частота ($_r$) равна:

При $^2ll ^2_0$ резонансная частота совпадает с собственной частотой колебаний $_0.$ Подставим вместо частоты правую часть выражения (11) в формулу (8), получим выражение для резонансной амплитуды вынужденных колебаний:

При небольшом затухании колебаний (если $^2ll ^2_0$) амплитуда при резонансе равна:

где $Q=frac<_0>$ — добротность колебательной системы, величина, характеризующая резонансные свойства колебательной системы. С увеличением добротности увеличивается амплитуда резонанса.

Видео:Физика 11 класс (Урок№7 - Свободные и вынужденные электромагнитные колебания. Колебательный контур.)Скачать

Примеры задач с решением

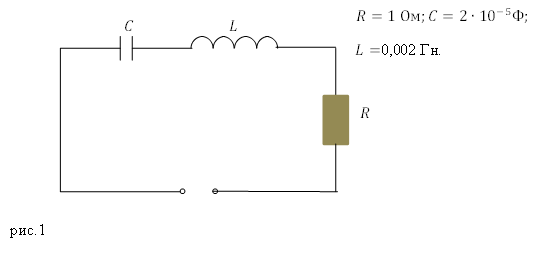
Задание. Какова добротность колебательного контура, представленного на рис.1?

Решение. Добротность электрического колебательного контура найдем как:

При этом собственная частота колебаний в таком контуре равна:

коэффициент затухания находим как:

Подставляет правые части выражений (1.2) (1.3) вместо соответствующих величин в (1.1), в результате, добротность представленного на рис. 1 контура найдем при помощи формулы:

Ответ. $Q=10$

Задание. Пружинный маятник выполняет вынужденные колебания в вязком веществе. Масса груза на пружине равна $m$, коэффициент упругости пружины $k$. Коэффициент сопротивления среды равен $r$. Систему заставляет совершать колебания сила $F=$Чему равна резонансная амплитуда заданных колебаний ($A_r$)?

Решение. Допустим, что груз совершает колебания вдоль прямой X, тогда уравнением данных механических колебаний будет выражение:

где коэффициент затухания равен $delta =frac$. Из функции, которая задает вынуждающую силу:

мы видим, что амплитуда силы равна единице:

Собственная частота колебаний груза на пружине:

Амплитуда при резонансе таких колебаний равна:

Видео:ЧК_МИФ ВЫВОД УРАВНЕНИЯ ВЫНУЖДЕННЫХ КОЛЕБАНИЙСкачать

Вынужденные электрические колебания

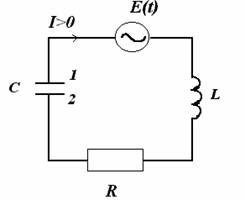
Рассмотрим электромагнитный колебательный контур, в котором помимо ёмкости, индуктивности, сопротивления есть ещё и генератор переменного напряжения, то есть источник электрической энергии. Очевидно, что в таком контуре со временем (это время обычно мало) установятся вынужденные колебания тока с частотой генератора и с постоянной амплитудой; подвод энергии от генератора будет в точности компенсировать потери энергии на сопротивлении.

Не будем учитывать внутреннее сопротивление генератора (будем считать, что у нас хороший, «идеальный» генератор). Получим уравнение для колебаний заряда на обкладках конденсатора. Для этого нам необходимо в закон Ома , который мы писали для затухающих колебаний, добавить в левую часть э.д.с. генератора E(t).

Дифференциальное уравнение вынужденных колебаний заряда в электромагнитном контуре в стандартном (каноническом) виде получается следующим:

или

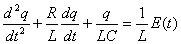
которое полностью аналогично уравнению вынужденных колебаний пружинного маятника . Э.д.с. генератора 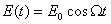. Поэтому сразу можем написать решение:

Резонансная частота колебаний заряда на обкладках конденсатора запишется также по аналогии с резонансной частотой механических колебаний маятника:

Напомню, что в электрическом контуре:

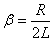
Обратите внимание, что резонансная частота для заряда зависит от коэффициента затухания, а, следовательно, от сопротивления.

Чаще нас интересуют не колебания заряда на конденсаторе, а колебания тока в цепи контура. Найдем эти колебания, продифференцировав заряд по времени:

В этом уравнении сделана подстановка —

Напомню, что — j является сдвигом фазы между напряжением генератора 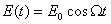и током в цепи. В такой записи знак минус показывает, что напряжение первично, а ток отстает по фазе.

Формулы для амплитуды тока и сдвига фаз выглядят так:

Существенное отличие колебаний тока от колебаний заряда состоит в том, что резонансная частота для тока не зависит от сопротивления; она просто равна собственной частоте свободных колебаний в контуре:

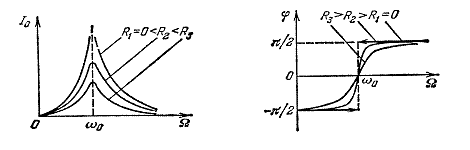
Колебания тока в цепи имеют аналогом не колебания механического маятника, а колебания его скорости. Резонансные кривые для амплитуды тока и зависимость сдвига фаз от частоты для различных сопротивлений — на графиках. Обратите внимание, что при резонансе сдвиг фаз между током и напряжением на генераторе отсутствует.

Посмотрим ещё раз на формулу для амплитуды колебаний тока. В числителе стоит амплитудное напряжение на генераторе (мы пренебрегаем внутренним сопротивлением генератора, поэтому его э.д.с. равна напряжению на его клеммах); в знаменателе — величина, имеющая размерность сопротивления. Она включает в себя не только активное сопротивление R, но и составляющую, зависящую от ёмкости и индуктивности контура и от частоты генератора. Эта величина носит название полного сопротивления контура, или импеданса контура Z:

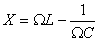
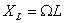
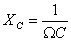
Величина носит название реактивного сопротивления, а её составляющие: — индуктивным сопротивлением; — ёмкостным сопротивлением.

Посмотрим, как ведут себя колебания тока и напряжения на различных участках контура.

Ток в цепи устанавливается со скоростью распространения электрического поля, то есть со скоростью света с. Время установления тока в цепи

l/c, где l — длина контура. Это время в реальных контурах много-много меньше, чем период колебаний. Поэтому мы считаем, что в каждый момент времени значения тока на всех участках цепи одинаково; колебания тока на сопротивлении, индуктивности и ёмкости происходят синхронно.

Иначе обстоит дело с колебаниями напряжения. Вычислим напряжение на каждом элементе контура и посмотрим, как они отличаются по амплитуде и фазе.

Видно, что напряжение на конденсаторе отстает на четверть периода от напряжения на сопротивлении, а напряжение на индуктивности на столько же по фазе опережает его. Напряжение на ёмкости и индуктивности всегда отличаются по фазе на полпериода. Наглядно сдвиг фаз на элементах цепи можно посмотреть на векторной диаграмме; из неё, в частности, ясно, почему импеданс вычисляется таким образом.

Общее падение напряжения на всех трех элементах цепи равно напряжению на клеммах генератора; поэтому угол j на диаграмме дает сдвиг по фазе между током и напряжением на генераторе.

Видео:Колебания в электрической цепи и дифференциальные уравненияСкачать

Вынужденные колебания. Переменный ток

Дадим определение понятию вынужденных колебаний.

Вынужденные колебания – это процессы, которые происходят в электрических цепях под воздействием периодического источника тока.

Основным отличием вынужденных колебаний по сравнению с собственными колебаниями в электрических цепях является то, что они являются незатухающими. Неизбежные потери энергии компенсируются за счет внешнего источника периодического воздействия, который не позволяет колебаниям затухать.

Видео:Свободные электромагнитные колебания. 11 класс.Скачать

Что такое переменный ток?

Переменный ток — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.

Рассмотрим случай, когда электрическая цепь способна совершать собственные свободные колебания с некоторой частотой ω 0 . Предположим, что к этой цепи подключен внешний источник, напряжение которого изменяется по гармоническому закону с частотой ω .

Частота свободных колебаний в электрической сети ω 0 будет определяться параметрами этой сети. Вынужденные колебания, которые установятся при подключении внешнего источника ω , будут происходить на частоте этого внешнего источника.

Частота вынужденных колебаний устанавливается не сразу после включения внешнего источника, а спустя некоторое время Δ t . По порядку величины это время будет равно времени затухания свободных колебаний в сети τ .

Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Цепи переменного тока

Цепи переменного тока – это такие электрические цепи, в которых под воздействием периодического источника тока происходят установившиеся вынужденные колебания.

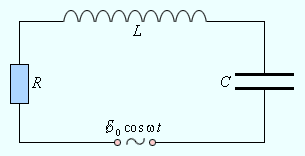
Рассмотрим устройство колебательного контура, в который включен источник тока с напряжением, изменяющимся по периодическому закону:

e ( t ) = ε 0 cos ω t,

где ε 0 – амплитуда, ω – круговая частота.

Фактически, это будет R L C -цепь.

Рисунок 2 . 3 . 1 . Вынужденные колебания в контуре.

Будем считать, что для изображенной на этом рисунке электрической цепи выполняется условие квазистационарности. Это позволит нам записать закон Ома для мгновенных значений токов и напряжений:

R J + q C + L d J d t = ε 0 c o c ω t.

Величину L d J d t принято называть напряжением на катушке индуктивности. Фактически, это ЭДС самоиндукции катушки, которую мы для простоты вычислений перенесли с противоположным знаком в левую часть уравнения из правой.

Уравнение вынужденных колебаний можно записать в виде:

u R + u C + u L = e ( t ) = ε 0 cos ω t.

где u R ( t ) , u C ( t ) и u L ( t ) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами U R , U C и U L . Напряжения при установившихся вынужденных колебаниях изменяются с частотой внешнего источника переменного тока ω .

Видео:Урок 361. Вынужденные колебания в последовательном колебательном контуреСкачать

Векторная диаграмма токов и напряжений

Для решения уравнения вынужденных колебаний мы можем использовать достаточно наглядный метод векторных диаграмм. Для этого используем векторную диаграмму, на которой с помощью векторов изобразим колебания определенной заданной частоты ω .

Давайте посмотрим, как построить векторную диаграмму токов и напряжений.

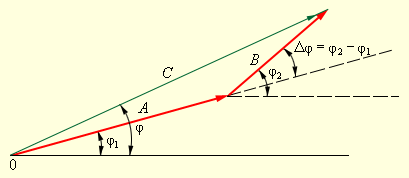
Рисунок 2 . 3 . 2 . Векторная диаграмма, на которой с помощью векторов изображены гармонические колебания A cos ( ω t + φ 1 ) , B cos ( ω t + φ 2 ) и их суммы C cos ( ω t + φ ) .

Наклон векторов к горизонтальной оси определяется фазой колебаний φ 1 и φ 2 , а длины векторов соответствуют амплитудам колебаний A и B . Относительный фазовый сдвиг определяет взаимную ориентацию векторов: ∆ φ = φ 1 — φ 2 . Для того, чтобы построить вектор, изображающий суммарное колебание, нам необходимо использовать правило сложения векторов: C → = A → + B → .

При вынужденных колебаниях в электрической цепи для построения векторной диаграммы напряжений и токов нам необходимо знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для любого участка цепи.

Источник переменного тока может быть подключен к:

катушке индуктивности L ;
резистору с сопротивлением R ;
конденсатору с емкостью С .

Рассмотрим эти три примера подробнее. Будем считать, что напряжение на резисторе, катушке и конденсаторе во всех трех случаях равно напряжению внешнего источника переменного тока.

Резистор в цепи переменного тока

J R R = u R = U R cos ω t ; J R = U R R cos ω t = I R cos ω t

Мы обозначили амплитуду тока, который протекает через резистор, через I R . Соотношение R I R = U R выражает связь между амплитудами тока и напряжения на резисторе. Фазовый сдвиг в этом случае равен нулю. Физическая величина R – это активное сопротивление на резисторе.