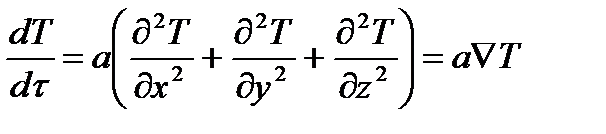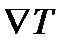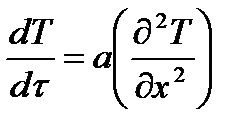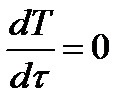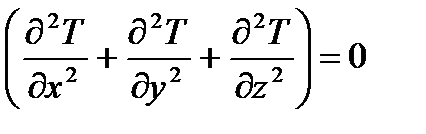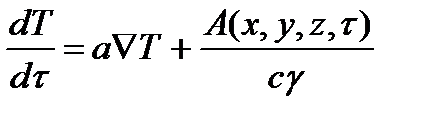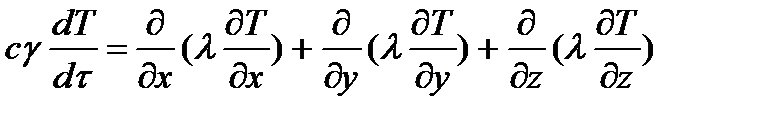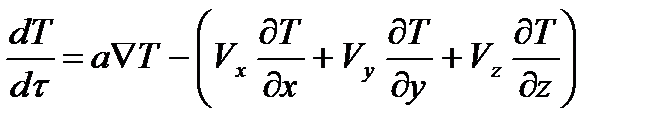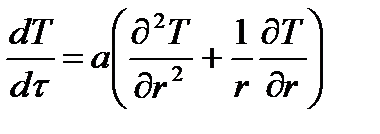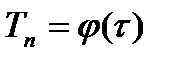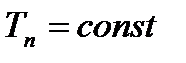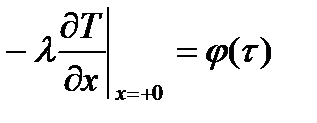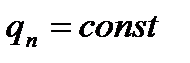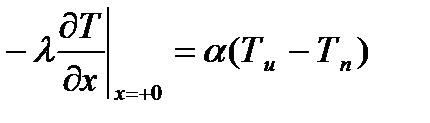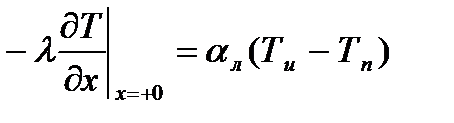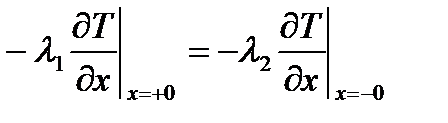Дифференциальное уравнение теплопроводности в прямоугольных координатах (8 видео)

Дифференциальное уравнение теплопроводности и его частные случаи

В трехмерной системе координат дифференциальное уравнение теплопроводности имеет вид

где а=λ/(сγ) – температуропроводность твердого тела,м 2 /с.

Выражение в круглых скобках правой части называется оператором Лапласа и обозначается

Рассмотрим частные случаи этого уравнения:

1) тепловой поток распространяется только вдоль оси х, тогда

2) в выделенном элементарном объеме твердого тела температура во времени не изменяется, т.е.

Называемое уравнением Лапласа, оно характеризует собой распределение температуры в элементарном объеме твердого тела при стационарном процессе переноса тепла (когда температура во времени во всех точках выделенного объема твердого тела остается постоянной).

3) внутренняя энергии выделенного элементарного объема твердого тела в точке с координатами х, yи zсуществует внутренний источник, выделяющий (или поглощающий) в единице объема за единицу времени количество тепла, равное А(х, y, z, τ), то дифференциальное уравнение теплопроводности имеет вид

4) теплопроводность твердого тела изменяется в рассматриваемом диапазоне температур, тогда

5) когда источник тепла перемещается со скоростью, компоненты которой равны V_x, V_y, V_z, тогда

Представленные уравнения относятся к прямоугольной системе координат.

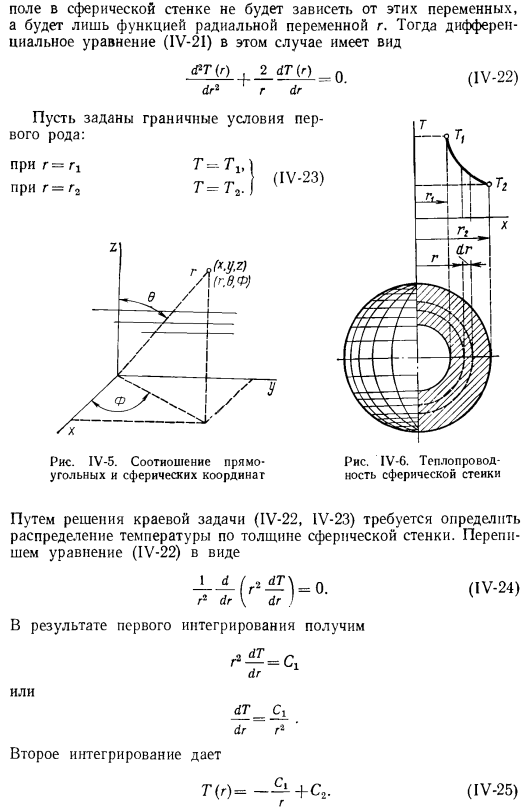
Дифференциальные уравнения теплопроводности в сферических и цилиндрических координатах имеют следующий вид:

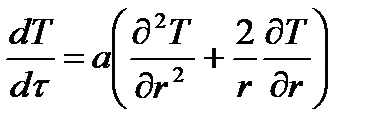
Краевые условия

Под краевыми условиями понимается совокупность начальных и граничных условий.

Начальным условием называется температурное поле в твердом теле в тот момент, с которого ведется отсчет времени температурного воздействия.

Граничным условием называется условие, определяющее процесс теплообмена на границе. Понятие «граница» включает в себя внешние поверхности, подверженные тепловому воздействию, и внутренние, расположенные на некотором удалении от внешних. Граничные условия складываются из сведений об условиях теплообмена на границе и сведений об изменении параметров источника теплового воздействия.

Различают четыре рода граничных условий:

1) если известен закон изменения температуры нагреваемой поверхности во времени

Частным случаем является постоянства температуры на поверхности, подверженной тепловому воздействию

2) если известна закономерность изменения во времени удельного теплового потока, поступающего к поверхности твердого тела

или

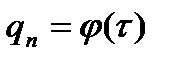
Индекс х=+0 указывает на то, что градиент температуры относится к точке тела, расположенной в непосредственной близости от поверхности.

Частным случаем имеет место при постоянстве удельного теплового потока

3) Если заданы температура источника теплового воздействия и интенсивность теплообмена на поверхности (теплоносителями являются жидкости и газы).

где α– коэффициент теплоотдачи, Вт/(м 2 К)

При установившемся режиме теплообмена коэффициент теплоотдачи можно принять постоянным.

Если нагрев твердого тела происходит за счет лучеиспускания, тогда

где 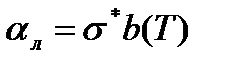, Вт/(м 2 К)

b(T) – коэффициент, зависящий от температуры источника и приемника лучистой энергии, К 3

— приведенный коэффициент лучеиспускания, Вт/м 2 ∙(К) 4

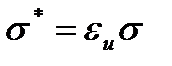
ϭ – постоянная Стефана-Больцмана, равная 5,67∙10 -8 Вт/м 2 К 4

ε – относительная излучательная способность (степень черноты) твердого тела.

4) при соприкосновении двух твердых тел с разными теплофизическими свойствами.

Во всех этих уравнениях в правых частях удельный тепловой поток, отводимый внутрь твердого тела от нагреваемой поверхности, в правой — математически сформулирована закономерность поступления тепла от источника к поверхности твердого тела.

Дата добавления: 2018-05-10 ; просмотров: 1860 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Содержание

Дифференциальное уравнение теплопроводности
Теплопроводность при стационарном режиме
Теплопроводность при стационарном режиме
📸 Видео

Видео:Уравнение теплопроводности в цилиндрических координатахСкачать

Дифференциальное уравнение теплопроводности

В учебниках по теплопередаче, в том числе и в [1], приводится вывод дифференциального уравнения температурного поля движущейся жидкости, уравнение энергии

(1.12)

где с_р, Дж/(кг×К) – изобарная теплоемкость; r, кг/м 3 – плотность; l, Вт/(м×К) – коэффициент теплопроводности; w_х, w_y, w_z – проекции вектора скорости движения жидкости; q_v , Вт/м 3 – объемная плотность внутреннего тепловыделения жидкости.

Уравнение (1.12) записано для случая l=const.

Дифференциальное уравнение температурного поля для твердых тел называется дифференциальным уравнением теплопроводности и может быть получено из (1.12) при условии w_х= w_y= w_z=0, с_р= с_v=с:

где — коэффициент температуропроводности, характеризует скорость изменения температуры в теле. Значения а = f (t) для различных тел приводятся в справочниках.

Дифференциальное уравнение теплопроводности

(1.13)

описывает нестационарное температурное поле твердых тел с внутренним тепловыделением (с внутренними источниками тепла). Такими источниками тепла могут быть: джоулева теплота, выделяемая при прохождении электрического тока по проводникам; теплота, выделяемая ТВЭЛами ядерных реакторов и т.д.

Дифференциальное уравнение теплопроводности (1.13), записанное в декартовых координатах, можно представить в цилиндрических (r, z, φ) и сферических (r, φ, ψ).

В частности, в цилиндрических координатах (r –радиус; φ – полярный угол; z — аппликата) дифференциальное уравнение теплопроводности имеет вид

(1.14)

Условия однозначности

Дифференциальное уравнение описывает множество процессов теплопроводности. Чтобы выделить из этого множества конкретный процесс, необходимо сформулировать особенности этого процесса, которые называются условиями однозначности и включают в себя:

· геометрические условия, характеризующие форму и размеры тела;

· физические условия, характеризующие свойства участвующих в теплообмене тел;

· граничные условия, характеризующие условия протекания процесса на границе тела;

· начальные условия, характеризующие начальное состояние системы при нестационарных процессах.

При решении задач теплопроводности различают:

· граничные условия первого рода, когда задается распределение температуры на поверхности тела:

· граничные условия второго рода, когда задается плотность теплового потока на поверхности тела:

· граничные условия третьего рода, когда задается температура среды t_ж и коэффициент теплоотдачи между поверхностью и средой.

В соответствии с законом Ньютона-Рихмана тепловой поток, передаваемый с 1м 2 поверхности в среду с температурой t_ж,

В то же время этот тепловой поток подводится к 1м 2 поверхности из глубинных слоев тела теплопроводностью

Тогда уравнение теплового баланса для поверхности тела запишется в виде

(1.15)

Уравнение (1.15) является математической формулировкой граничных условий третьего рода.

Система дифференциальных уравнений совместно с условиями однозначности представляет собой математическую формулировку задачи. Решения дифференциальных уравнений содержат константы интегрирования, которые определяются с помощью условий однозначности.

Контрольные вопросы и задания

1. Проанализируйте, какими способами передается теплота от горячей воды к воздуху через стенку батареи отопления: от воды к внутренней поверхности, через стенку, от наружной поверхности к воздуху.

2. Почему в правой части уравнения (1.3) стоит минус?

3. Проанализируйте с помощью справочной литературы зависимость λ(t) для металлов, сплавов, теплоизоляционных материалов, газов, жидкостей и ответьте на вопрос: как изменяется коэффициент теплопроводности с изменением температуры для этих материалов?

4. Как определяется тепловой поток (Q, Вт) при конвективной теплоотдаче, теплопроводности, тепловом излучении?

5. Запишите дифференциальное уравнение теплопроводности в декартовых координатах, описывающее трехмерное стационарное температурное поле без внутренних источников теплоты.

6. Запишите дифференциальное уравнение температурного поля проволоки, которая длительное время находится под напряжением при постоянной электрической нагрузке.

2. ТЕПЛОПРОВОДНОСТЬ И ТЕПЛОПЕРЕДАЧА
ПРИ СТАЦИОНАРНОМ РЕЖИМЕ

2.1. Теплопроводность плоской стенки
при граничных условиях первого рода

Дано:плоская однородная стенка толщиной δ (рис. 2.1) с постоянным коэффициентом теплопроводности λ и постоянными температурами t₁ и t₂ на поверхностях.

Определить:уравнение температурного поля t=f (x) и плотность теплового потока q, Вт/м 2 .

Температурное поле стенки описывается дифференциальным уравнением теплопроводности (1.3) при следующих условиях:

· т. к. режим стационарный;

· т.к. отсутствуют внутренние источники теплоты;

· т.к. температуры t₁ и t₂ на поверхностях стенки постоянны.

Температура стенки является функцией только одной координаты х и уравнение (1.13) принимает вид

(2.1)

т.к. коэффициент температуропроводности стенки а ≠ 0.

Граничные условия первого рода:

при х=0 t= t₁ ,	(2.2)
при х= δ t= t₂.	(2.3)

Выражения (2.1), (2.2), (2.3) являются математической постановкой задачи, решение которой позволит получить искомое уравнение температурного поля t= f (x).

Интегрирование уравнения (2.1) дает

При повторном интегрировании получим решение дифференциального уравнения в виде

t=с₁х+с₂.

(2.4)

Из уравнения (2.4) при условии (2.2) получим

а при условии (2.3)

Подстановка констант интегрирования с₁ и с₂ в уравнение (2.4) дает уравнение температурного поля

(2.5)

по которому можно рассчитать температуру по толщине стенки на любой координате 0 2 ; t₂, t₃.

При стационарном режиме и постоянных температурах поверхностей стенки тепловой поток, передаваемый через трехслойную стенку, можно представить системой уравнений:

	(2.8)
	(2.9)
	(2.10)

(2.11)

Сложив левые и правые части уравнений (2.11), получим расчетную формулу для плотности теплового потока, передаваемого через трехслойную стенку

(2.12)

Температуры на границах слоев t₂ и t₃ можно рассчитать по уравнениям (2.8) – (2.10) после того, как найдена плотность теплового потока (q) по (2.12).

Общий вид уравнения (2.12) для многослойной плоской стенки, состоящей из п однородных слоев с постоянными температурами на наружных поверхностях 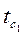и , имеет вид

(2.13)

Средний коэффициент теплопроводности многослойной стенки называют эффективным (λ_эф). Он равен коэффициенту теплопроводности однородной стенки, толщина и термическое сопротивление которой равны толщине и термическому сопротивлению многослойной стенки

(2.14)

2.2. Теплопроводность цилиндрической стенки
при граничных условиях первого рода

Дано:Однородная цилиндрическая стенка (стенка трубы) с внутренним радиусом r₁, наружным – r₂, длиной , с постоянным коэффициентом теплопроводности λ, с постоянными температурами на поверхностях t₁ и t₂.
(рис. 2.3).

Определить: уравнение температурного поля
t = f (r), тепловой поток, передаваемый через стенку
Q, Вт.

Дифференциальное уравнение теплопроводности в цилиндрических координатах (1.14) для условий данной задачи:

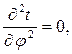
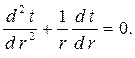(2.15)

Граничные условия первого рода:

при r=r₁ t=t₁ ,	(2.16)
при r=r₂ t=t₂ .	(2.17)

Порядок решения системы уравнений (2.15) – (2.17) тот же, что и в случае плоской стенки: находится общий интеграл дифференциального уравнения второго порядка (2.15), который содержит две константы интегрирования
с₁ и с₂ . Последние определяются с помощью граничных условий (2.16) и (2.17) и после подстановки их значений в решение дифференциального уравнения (общий интеграл) получаем уравнение температурного поля цилиндрической стенки t = f (r) в виде

(2.18)

где r₁ r r₂ – текущий радиус.

Нетрудно убедиться, что при подстановке в (2.18) r= r₁ получим t=t₁ , при r=r₂ получим t=t₂. Распределение температуры по толщине цилиндрической стенки, в соответствии с (2.18) подчиняется логарифмическому закону (рис. 2.3).

Для определения теплового потока воспользуемся законом Фурье:

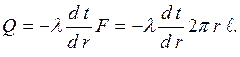(2.19)

Если взять производную от правой части уравнения (2.18) и подставить в (2.19), получим расчетную формулу для теплового потока цилиндрической стенки

(2.20)

В технических расчетах часто тепловой поток вычисляется для 1 м длины трубы:

и называется линейной плотностью теплового потока.

Запишем уравнение (2.20) в виде

где – термическое сопротивление теплопроводности цилиндрической стенки.

Для трехслойной цилиндрической стенки (трубы, покрытой двумя слоями тепловой изоляции) с известными постоянными температурами поверхностей (t₁ и t₄), с известными геометрическими размерами (r₁ , r₂, r₃, r₄ , ) и коэффициентами теплопроводности слоев (λ₁, λ₂, λ₃) (рис. 2.4) можно записать следующие уравнения для теплового потока Q:

(2.21)

Совместное решение системы уравнений (2.21) дает расчетную формулу для теплового потока, передаваемого через трехслойную стенку при заданных температурах на поверхностях,

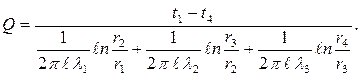(2.22)

Температуры на границах слоев (t₂, t₃) можно рассчитать по уравнениям (2.21).

Для многослойной цилиндрической стенки, состоящей из п слоев, формулу (2.22) можно записать в общем виде

(2.23)

Эффективный коэффициент теплопроводности для многослойной цилиндрической стенки, как и для многослойной плоской стенки, определяется из равенства суммы термических сопротивлений многослойной стенки термическому сопротивлению однородной стенки той же толщины, что и многослойная. Так, для двухслойной тепловой изоляции трубы
(рис. 2.4) эффективный коэффициент теплопроводности (λ_эф) определ ится из равенства

2.3. Теплопроводность плоской и цилиндрической стенок
при граничных условиях третьего рода (теплопередача)

Граничные условия третьего рода состоят в задании температуры жидкости (t_ж) и коэффициента теплоотдачи ( ) между поверхностью стенки и жидкостью.

Передача тепла от одной жидкости к другой через разделяющую их стенку называется теплопередачей.

Примерами теплопередачи служит перенос теплоты от дымовых газов к воде через стенку трубы парового котла, перенос тепла от горячей воды к окружающему воздуху через стенку батареи отопления и т.д.

Теплообмен между поверхностью и средой (теплоносителем) может быть конвективным, если теплоноситель – жидкость (вода, нефть и т.д.) или радиационно-конвективным, когда теплота передается путем конвективного теплообмена и излучением, если теплоноситель – газ (дымовые газы, воздух и т.д.).

Рассмотрим теплопередачу через плоскую и цилиндрическую стенки при условии только конвективного теплообмена на поверхностях. Теплопередача с радиационно-конвективным теплообменом (сложным теплообменом) на поверхностях будет рассмотрена позже.

Плоская стенка(рис. 2.5)

Дано:

Плотность теплового потока q описывается следующими уравнениями в зависимости от способа передачи теплоты:

– от горячей жидкости к стенке

(2.24)

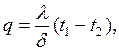(2.25)

– от стенки к холодной жидкости

(2.26)

Записав уравнения (2.24) – (2.26) в виде

(2.27)

и сложив почленно правые и левые части уравнений (2.27), получим формулу для расчета теплопередачи (q, Вт/м 2 ) через плоскую стенку в виде

(2.28)

Величины называются термическими сопротивлениями теплоотдачи. Они прямо пропорциональны перепадам температур .

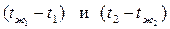
Температуры на поверхностях стенки t₁ и t₂ можно рассчитать по уравнениям (2.24) – (2.26) после того, как определена плотность теплового потока (q) по уравнению (2.28).

Формулу (2.28) можно записать в виде

(2.29)

где — коэффициент теплопередачи плоской стенки,характеризует интенсивность процесса теплопередачи.

Теплопередача через многослойную плоскую стенку рассчитывается по формуле

(2.30)

Цилиндрическая стенка(рис. 2.6)

Дано:

Для цилиндрической стенки, по аналогии с плоской стенкой, можно записать следующую систему уравнений:

	(2.31)
	(2.32)
	(2.33)

где — площади внутренней и наружной поверхностей трубы.

Записав уравнения (2.31) – (2.33) относительно разностей температур, а затем сложив правые и левые части уравнений, получим формулу для расчета теплопередачи (Q, Вт) через цилиндрическую стенку в виде

(2.34)

Температуры на поверхностях стенки t₁ и t₂ рассчитываются по уравнениям (2.31) – (2.33).

Формулу (2.34) также можно представить в виде

где – коэффициент теплопередачи цилиндрической стенки.

Для металлических труб с 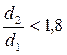можно пренебречь кривизной стенки и теплопередачу рассчитать по формулам для плоской стенки:

Видео:Уравнение в частных производных Уравнение теплопроводностиСкачать

Теплопроводность при стационарном режиме

Видео:Уравнение теплопроводности в цилиндрических координатахСкачать

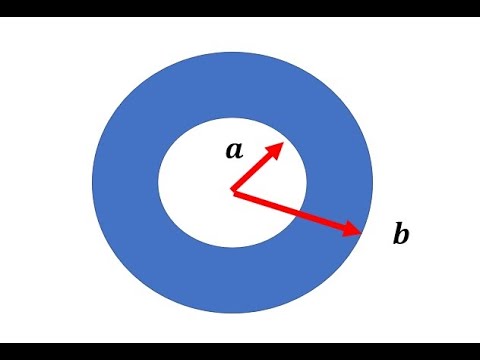
Теплопроводность при стационарном режиме

В установившемся состоянии температурное поле T (x, yₜr, t) не зависит от времени. То есть,^ = 0.Дифференциальное уравнение теплопроводности (II-55)^ = aV2T (IV-I) DX is (П-56 И Р-57) Eh2du * Ldz2(IV-2)для решения конкретной задачи в Формулу (IV-2) необходимо добавить соответствующее граничное условие. Рассмотрим несколько простых случаев Определение стационарного температурного поля для объектов различной формы. § 1.

To рассмотрим теплопроводность тела плоская стенка неограниченная плоская стенка с подходящим температурным полем Его толщина равна 6, его поверхность параллельна плоскостям Y, z декартовой системы координат и находится при x = 0 и x = 6(рис. IV-1).Давайте поддержим его этими поверхностями Соответственно, задаются температуры 7 и Т₂, то есть граничные условия типа 1(Глава 2,§ 5).

Выражение (IV-3) немедленно интегрируется. Людмила Фирмаль

Если Γ и T₂ не зависят от координат y и z, то, очевидно, искомое температурное поле Уравнение (IV-2), которое зависит от этих координат и определяет температуру T (x), принимает вид

= 0 (IV-3) dx2V ’при граничном условии. Г= 7 при x-0 (IV-4) T-X Tn-6.Общая форма решения T (x)=C₁X4-C₂,(1V-5).Где C. И C₂-произвольная константа, определяемая из граничного условия. (IV-4).фактически, если вы установите x = 0 в(IV-5)и используете первую формулу (IV-4), вы получите 2-е условие (IV-4) и (на основе) Л=С₂, (IV-6), x = 6. (IV-6) есть фига IV -!.

Теплопроводность плоской стенки т = С.6+С₂ = С.6+ 7 ′., (IV-7) где C = ^, 16 наконец, решение уравнения (IV-3) при граничном условии(1V-4) видно из (IV-8)(1V-8 T(x)линейно зависит от x, и эта зависимость T (x)= f (x)показана на рисунке вдоль толщины стенки. IV-1.Тепловой поток q можно определить по закону Фурье (1-3): q = — XgradГ, или В нашем случае, дифференцируя распределение температуры по толщине стенки (IV-8), мы видим, что dxowhence (IV-9) получается из Формулы (IV-9), которая равна 7′. > Flux тепловой поток положительный, то есть он направлен вдоль положительного направления оси X. В 7 7 ′ 2 он направлен в противоположную сторону.

Этот результат является результатом второго закона термодинамики. В частности, тепло передается от нагретого тела к неотапливаемому. Количество тепла, проходящего через стенку за единицу времени, легко вычисляется с помощью (IV-9), q = ^ = X (T₁ — ^ 7′) 4 -/⁷. (1V-10) перепишите уравнение Фурье (P-54) в цилиндрической системе координат с цилиндрическим wall. To сделайте это, декартовы координаты и Цилиндрические координаты (рис. IV-2), x = r cos B, y = r sin B, z = R.

После проведения изменения этой переменной форма уравнения цилиндрической системы координат (P-54) равна dT / dTT- = а-э ДГ * _ ДТ Р ДГ &т р * ДВ. Рассмотрим 1D процесс стационарной теплопроводности на бесконечной цилиндрической стенке (рис. IV-3).Если на рисунке IV-2.Соотношение Прямоугольные и цилиндрические координаты T рис. 1в-3.Теплопроводность цилиндрической стенки, внутренней (r = r) и внешней (r-RJ) поверхности стенки.

Они не зависят от угла Вига, искомое температурное поле не зависит от этих переменных, и если оно стационарно, то уравнение (IV-11) имеет вид (FT (g) 1 dT ® Q dr-r dr (IV-12) при заданном граничном условии типа 1 R = r₁T =Г= = ₂ ₂t =t 決定 определяет распределение температуры по всей толщине стенки. Формула (IV-12) Переписывание (IV-13) (IV-14) Теперь 1 раз integration. As в результате после 2-го интеграла получаем общее решение уравнения. (IV-14): T(g)= CJn g 4-C₂. (IV-15) постоянная интеграция C! И С₂ должно быть определено из граничного условия(IV-13).Р= rxT₁=С₁1пг₁+С₂]и (IV-16)⁼ГГ2Т2⁷ ⁷1ПГ₂4″ С₂.

Если вы решите для (IV-16) относительно Ca, вы найдете первую интегральную константу Ca≥1n-и вторую константу Ca₂C = Tj-Cjlnr ^-br ^ linr ^ 1гг-ЛПП. ’1′ 1 замена Найдя значения Cb и C₂ в Формуле (IV-15), получим искомое распределение температуры по всей толщине цилиндрической стенки In-T ® =Tₗ+(T,-T₁) — I. (IV-17) ’ I следовательно T(g） Логарифмически зависит от радиусной координаты r. плотность теплового потока q определяется по закону Фурье. Основываясь на (IV-17), существует проходящее количество тепла.

Цилиндрическую стенку, которая указывает на единицу длины трубы, можно определить по формуле: Q-qF-q-2nr = inK (T1-T.). (IV-19) — — — в ri Q естественно не зависит от R. Тепло не будет накапливаться anywhere. By по аналогии с многослойной цилиндрической стенкой(1-6) принимается тепловое сопротивление многослойной цилиндрической стенки (рис. IV-4). Равна сумме тепловых сопротивлений отдельных слоев. На основе этого утверждения можно использовать формулу (IV-19) для создания формулы, определяющей количество тепла, которое проходит через нее.

Q-присваивается единице длины стены. Преобразуйте уравнение сферической стенки (P-54) в сферическую систему координат. Используйте его для этого Следующая зависимость между Декартовыми координатами и сферическими координатами (рис. IV-5): x = r sinccosф, y = r sin 8 sinФ, z = r cos 8.Проводимость многослойной цилиндрической стенки В В сферической системе координат форма уравнения (P-54) равна dTha2?Как туда добраться, 2 at, 1 d F. dT ₜdtL3r3g dr’g2sinea ae /1_g2sin26dF2] (IV-2I) рассмотрим стационарный процесс Теплопроводность внутренней поверхности (r = rx) и наружной поверхности (r =r₂) сферической стенки (оболочки) (рис. IV-6) соответственно.

Т₂. Семь Т₂ является постоянным. То есть она не зависит от направления, которое определяется углом 8 и cp. Поэтому требуемое температурное поле сферической стенки не зависит от этих переменных、 Функция радиальной переменной r. вид дифференциального уравнения (1V-2I) в этом случае равен IV-5.Корреляция декартовых и сферических координат IV-6. Для решения задачи теплопроводности граничного значения сферической конформации (IV-22, IV-23) необходимо определить распределение температуры по всей толщине сферической стенки. Переписывание Формулы (IV-22） (Ив-24) m2dr доктор! сначала в результате первого интеграла получается dr r* второй .

Интеграл дает Г ® =Г (IV-25).Общее использование граничных условий (IV-23) Решите уравнение (1V-25) для определения любых констант Ci и C2:r — — — rx m — — ^ + c2, T A = — — — ^ + C2. для r = r2 G # Если вы решите эти уравнения относительно C и C₂, вы получите 1 _ _ _ _ _ 1_ Заменяет G «-G1 G1 gg и G₂-G1 Cx и C₂ общим решением (IV-25).Упрощенный, наконец m = r = +(T₁-t₁) r yr от Gg-gx (IV-26) (IV-26), температура T (g） Она изменяется по толщине сферической стенки вдоль гиперболы. Определите тепловой поток из раствора (IV-26) — CL-L) ’ 1 ’» количество тепла, передаваемого через сферу 1 yy-yy.

В единицу времени, 2 =₉Г=₉.4лг2 = 4ях (л-Г₂) -!он равен а^ -. (IV-27) / ■ » — ’ 1 не зависит от r по тем же причинам, что и для цилиндрических стенок.§ 2.Теплопроводность тела с Внутренние источники тепла процессы теплопроводности в твердых телах обусловлены внешними условиями, то есть распределением температуры и теплового потока Подвод (отвод) тепла от поверхности тела и образующейся в результате внешней среды.

Математически это выражалось в выделении определенных граничных условий на поверхности тела. Рассмотрим процесс теплопередачи, когда помимо такого внешнего источника тепла существует еще и внутренний источник (сток), который распределяется определенным образом. Объем тела. Вы можете привести много примеров таких processes. It ограничивается упоминанием о том, что тепло образуется, когда электрический ток протекает через проводник.

Тепло Количество тепловыделяющих элементов выделяется и в замедлителях реактора. Когда в рассматриваемом объеме тела происходит определенная химическая реакция, он высвобождается(поглощается） В таком вопросе теплопроводности желательным обычно является распределение температуры внутри тела субъекта, а мощность внутреннего источника тепла (стока) принимается во внимание Это было дано. Мощность источника (стока) — это количество тепла, которое выделяется (поглощается) единицей объема тела за единицу времени.

Эта сумма показана в qᵥ、 Килоджоули / кубический метр / сек (kA s /l13-sec).В зависимости от характера процессов, происходящих в рассматриваемом теле, источник тепла (Сток) может выбираться по-разному. Или концентрируйтесь на определенной части или точке объема тела в течение определенного времени, или равномерно распределяйтесь по всему объему, в зависимости от температуры. Уравнения Теплопроводность при наличии внутреннего источника тепла описывается в виде cp% — = Ky’t +qᵥ. (IV-28) изменение теплоты на единицу объема за 01 единицу времени、 .

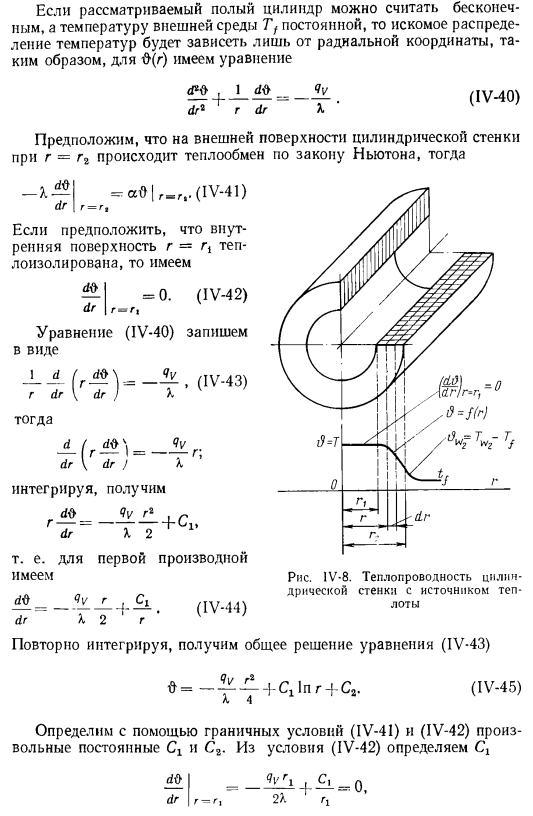
Здесь имеет место не только процесс теплопроводности, который является первым членом в правой части формулы (IV-28), но и выделение (поглощение) тепла в единице объема qv, которое мы рассмотрим ниже. Рассматривается задача о постоянном во времени и равномерно распределенном по всему источнику тепла. Теплопроводность бесконечной стенки с внутренним источником тепла плоскость YY и неограниченная стенка (рисунок IV-7) очищаются с обеих сторон при постоянной температуре жидкости Tf. Коэффициент теплопередачи .

A и выход равномерно распределены Объем qᵥ стенки источника тепла равен given. It необходимо найти распределение температуры по всей толщине стенки. Состояние поверхности стенки x = — I n x = I является постоянным, то есть, В зависимости от координат y и z температура будет функцией только от x, а уравнение (IV-28) будет иметь вид xs_ ⁼vv IV IV’2⁾.Однако, — 1 — = а(Тх ₌ / — г.) (IV-30) dx x = 1 * последний и В других случаях источник тепла может зависеть не только от координат, но и от температуры. Для аналогичных условий симметрия на поверхности x—I .

Температурное поле для плоскости x = 0 может быть заменено условием dx x-o (IV-31).От температуры очищающего раствора вводят Счетную температуру (IV-32)и затем кромку Задача (IV-29 напишите qydx2X dx x> = Q. интегрируйте уравнение (IV-33).d / _ _ _ _ _ Chu ’dx dx j X и IV-31) re — (IV-33) (IV) B 7 1 Tf X g *’ / 1 1 x рисунок IV-7.Теплопроводность плоской стенки с источником тепла после первого уплотнения приобретает вид (IV-35), а после второго уплотнения общий раствор (IV-33) получается в виде x 4-Cj. х 4-Cₜ. Граничное условие (IV-36) (IV-34) используется для определения констант /

Cx и C₂. Из (IV-35) и 2-го граничного условия (IV-34), C,= 0. dx (IV-37) в начале условия, где x = I (IV-34), получаем 2A. то есть, подставляя значение константы произведения С₂ в (IV-37), получаем решение вида (IV-38). Решение квадратично зависит от x (параболически).С другой стороны, если не было внутреннего источника, зависимость была линейной[ссылка(Iv-8)].Представьте себе решение(IV-38) Обобщенная координата. Если вы выбираете как раздел/2Liv, то все термины (IV-38), количество с размером температуры, и половина своей толщины / характерного размера стены.

Левая сторона (IV-39) (IV-39) является безразмерной температурой поиска. А правая сторона содержит независимые переменные в виде безразмерных координат-y и комплексных параметров Виде био-стандартом. Следовательно, (IV-39)-это (P1-13a) * q.. l2(характеристическая температура Oo = — ^ y — |является специфической функцией вида, которая получается на основе анализа） Решите уравнение (IV-33) с граничным условием (IV-34).Теплопроводность цилиндрической стенки с источником тепла делают цилиндрическую стенку (рис. IV-8) однородной.

Распределенный по всей его толщине источник тепла охлаждается снаружи жидкостью с температурой Tf коэффициентом теплопередачи a и прочностью источника тепла qᵥ.It требуется Найти распределение температуры= = T-Tf по толщине стенки. •В этом случае вводить параметрические критерии не требуется. Если полый цилиндр в вопросе можно рассматривать Для d (g) используется уравнение dr2g, поскольку если температура окружающей среды.

Есть рисунок 1В-8.Теплопроводность цилиндрической стенки с источником тепла chu g, Cx dr X 2. Людмила Фирмаль

Tf постоянна, то желаемое распределение температуры зависит только от радиальных координат. на внешней поверхности цилиндрической стенки dr X (IV-40) r = r, предполагая, что теплообмен происходит по закону Ньютона,=: ab |(IV-41)dr r =rₜ (Ив-42) рублей. df> dr тогда dr dr J X если записать формулу (IV-40) в виде интеграла, то получится 1 2. ′ g (IV-44) итерационно интегрируют и получают общее решение уравнения (IV-43) 0 =—+Cilⁿr+ C»- Используйте (IV-45) A 4 граничных условия (IV-41) и (IV-42) для определения любых констант Cx и C₂.

Из условия (IV-42), M, C, ₀dr r ^rₜ2X q», то есть из условия (IV-41) определим С₂ отсюда (IV-45) и подставив значение и С₂ получим конкретное решение формулы(IV-40). Представьте себе решение (IV-46) с цилиндрической стенкой (IV-46) с обобщенными координатами(1V-46).Разделите все члены (IV-46) и выберите внешний (охлаждающий) радиус в качестве характерного размера С поверхности r2 цилиндрической стенки получаем O 4X. левая сторона (IV-47) является безразмерной искомой температурой, как и в(1V-39), а независимая переменная переходит в правую сторону. Джи! составной параметр в виде ссылки Biot, в виде g₂.

Как и в случае (IV-39), Формула (IV-47)является специфической функцией вида(1P-13a).Для цилиндрических стержень (r,= 0)обобщенная зависимость (IV-47) принимает вид (IV-48)§ 3. Теплопроводность тела с 2-мерным температурным полем 2-мерное температурное поле T-f (x, y) Получение аналитических решений, удовлетворяющих дифференциальным уравнениям и граничным условиям, рекомендуется для объектов простой формы. Для тела сложной формы решением является.

Громоздкие, в некоторых случаях недоступные. Тогда для фактического расчета аналитическое решение либо упрощается одним из численных методов аппроксимации, либо ставится задача Решайте численно в электронных вычислительных машинах и тому подобное. Мы найдем аналитическое решение дифференциального уравнения для некоторых граничных условий, которые будут представлены ниже.

Для двумерного Формат температурного поля уравнения T = T (x, y) (P-54) имеет вид^ 4-^ = 0. в качестве решения dhadu1 (IV-49)мы применяем метод разделения переменных. Найти решение уравнения в виде Произведение 2 функций, то есть T = f(x, y)= X (x)Y (y), (IV-50), где X (x) — функция только переменной x. Y (y) является функцией только переменной y. Формула т из(IV-50) (1V-49), после деления на X и Y, _dtY__________ 1 вы получите d * XY dy * XX1 (IV-51).Поскольку левая сторона (IV-51) не зависит от x и равна значению (правая сторона), это если вы не зависите от y, общие (оба) значения не зависят от x или y. таким образом, общее значение (для обеих частей) уменьшается до постоянного значения. Это полезно для принятия формы k2.

Как и в (IV-56), напишите общее решение (IV-53) X = Cxeⁱkx+C₂e〜ⁱkx, (IV-59).Здесь (и С₂-произвольные константы. Однако формулы e1x и е-1 actually на самом деле фактические значения х, кроме Х = 0.Используя Эйлера официальный e±ТТХ₌потому что£Х±З Син х (ИЖ-60) (ИЖ-59)* х — сов / экс-ЖБ грех КХ. (ИЖ-61） Можно написать общее решение Формулы (IV-59) на основе (IV-60) в виде T = x XU =(AcosЛх4-Bsin KX) (SEC>〜J-de-K>) (IV-62).

Применяйте его для решения конкретных задач. Теплопроводность плоских стенок с 2-мерным температурным полем рассмотрим конкретную задачу теплопроводности плоских стенок (рис. IV-9).Пусть T-форма температурного поля на стене = /(х,//), температуры в направлении оси Z во всех точках (вдоль стены толщина) X = СЈ е ’ * — r4C₂e -и KX = Ки(coskx + я грешу опций)-| −4- СГ (потому что / с GX-мне грех КХ)=(СЈ-Ф-C₂) потому что с KX + я (Cₜ-C₂） грех КХ — = а потому что КХ ^ — ПБ грех КХ -, (а = с ^ СГ, 5 = ^ −0.).

Тот же смысл. Избыточная температура(гл. Уравнение Лапласа (P-56) для этой задачи в 111,§ 2) имеет вид dx2du2. Граничное условие типа 1 O = T-Ta = 0 задается для x = 0 и x = L. где 0-искомая избыточная температура стенки. Ta-поддерживается температура боковой стенки Постоянный. (IV-63) (IV-64) 0 — > 0 как y — > — oo. (IV-66) (рисунок 1V-9) рисунок IV-9. Теплопроводность в 2D температурном поле, Т= / (*•У) где 7 — температура на нижнем конце (см. Рисунок). 1В-9) стены поддерживаются постоянными.

Решением уравнения (IV-63) будет уравнение (1V-62). в последнем случае абсолютная переменная температуры T заменяется избыточной переменной F. Используя граничные условия (IV-64 и IV-66), определите постоянные коэффициенты A, B, C, D. Из первого условия(1V-64) выполните x-0 и A-0. x = 0 должен быть равен нулю, но cosx |z₌ ₀ = coso = 1, то есть если он не равен пуле, то коэффициент a должен быть равен нулю. Поскольку нас интересуют нетривиальные решения, а именно, они не равны нулю Аналогично коэффициент B равен нулю, поэтому если x = L, то требуется sinkL 0.Значение нетривиального решения, удовлетворяющего границе уравнения (IV-63) .

Условие (IV-64) называется собственным значением, а нетривиальное решение этой задачи называется собственной функцией, соответствующей заданному eigenvalue. So кл- ПЛ, вот н= 0、1、2、3、…в результате k>/ / L, k₂-2n / L,…kₙ= !! Си.,…Из условия (IV-66) следует, что коэффициент C = 0 (y — * oo, если e * y неограничен） Рост.) При A = 0, C-0 решение(1V-62) не может принимать вид^-BDe sin ^-^-x ^ =£e sin ^ — ^ ^ x ^ (IV-67) решение (IV-67) удовлетворяет дифференциальному уравнению (1V-63). любое натуральное значение n. из полученного решения (IV-67) видно, что для 7 -Ta 0 условие (IV-65) не выполняется для выбора E-En. 0 после этого .

Единственным решением проблемы является тривиальное решение 0 = 0.С другой стороны, сумма любых 2 (и, следовательно, любого конечного числа) решений линейных однородных производных Уравнение также является решением. Если мы суммируем число решений типа (IV-67) до бесконечности, то увидим, что мы можем выбрать E = En так, чтобы условие (IV-65) было выполнено(или、 Условие (IV-66)] и бесконечная сумма d = 2£e_T «sin (- ^x’) (IV-68) сходятся, а краевые задачи (IV-63), (IV-64), (IV-65) и (IV-66) сходятся.

Как найти Ep Используйте граничное условие (IV-68) (IV-65). если y = 0, то форма выражения (IV-68) равна (IV-69). чтобы понять формулу (IV-69), вспомним следующее положение из математики. Функция является F (x)с периодом 2n дифференцируема или, по крайней мере, кусочно дифференцируема и может быть расширена рядом Фурье следующих форм: где a0, an и bn Величина, которая называется коэффициентом ряда Фурье и определяется по формуле: lnp-j /(x) cosnxJx (l = 1,2 t 3,…(IV-71) — — — l l°0 = ’ T (IV-713) — — — l l 6n = — J — (F (x) sin nxdx(n = l, 2, 3. ). л.(ИЖ-72) с / — — — Л. Если F (х) нечетная функция (χχ) потому что NX-это странно. Помнишь? В случае нечетной функции выполняется равенство f (- x)= — f (x).

Тогда об этом л§f (x) dx = 0-и, следовательно, в случае (IV-71) an = jf (x) cos nx dx = 0(n = 1, 2, 3,…). — Я имею в виду… Вид ряда Фурье нечетных функций (IV-70) имеет вид f(x)= S b sin px. Чтобы определить bn из (IV-73) n = I (IV-72), для четной функции используйте равенство f (- X) 0), то, изменив переменную, можно переписать Формулы (IV-73) и (IV-75) в виде ZW = BS&». грех (- ПХ） (IV-76) и L sino теперь возвращаются к Формуле (IV-69).

Положим Dx)=в этом случае Формулы (IV-69)и(IV-76) идентичны. Таким образом, выражение (IV-69) представляет собой ряд Фурье следующих констант: Интервал 10, ZJ(Z7 > 0).Константа En равна Ln и по формуле (IV-77) y-x)/ x, где n = 1,2,3……….(IV-77) 0 n = 1, 3, 5, cos pl—1 = n = 2, 4, 6, cos pl-4-1 и En = 0.Конкретные решения (IV-68) могут быть записаны в окончательном виде (IV-78).Здесь мы используем следующие результаты: если функция Dx) с периодом разлагается равномерно В случае сходящегося ряда последний должен быть ближе к Фурье. (Серия (IV-78) четко сходится равномерно.

Отметим, что согласно (IV-78), температура стенки в любой точке не зависит. Теплопроводность в случае учета отсутствия теплового потока на стене. Из полученного решения также ясно, что если = 0, то решение 0 = 0.§ 4. При передаче тепла от жидкости (а.) до падения теплопроводности в ребрах определенных пересечений через сплошную стенку к газу (А₂), общее тепловое сопротивление!K определяется. 4 -= по формуле (1-12)-+ 4-± ИЖ — ⁷⁹ > к-Аль — Xa₂ последний срок 1 /a₂ вносит наибольший вклад в общее тепловое сопротивление, 1, а в некоторых случаях и 2-х значное число больше, чем первых 2-х значное число членов 1 / aP обычно, a₂ не может быть увеличен.

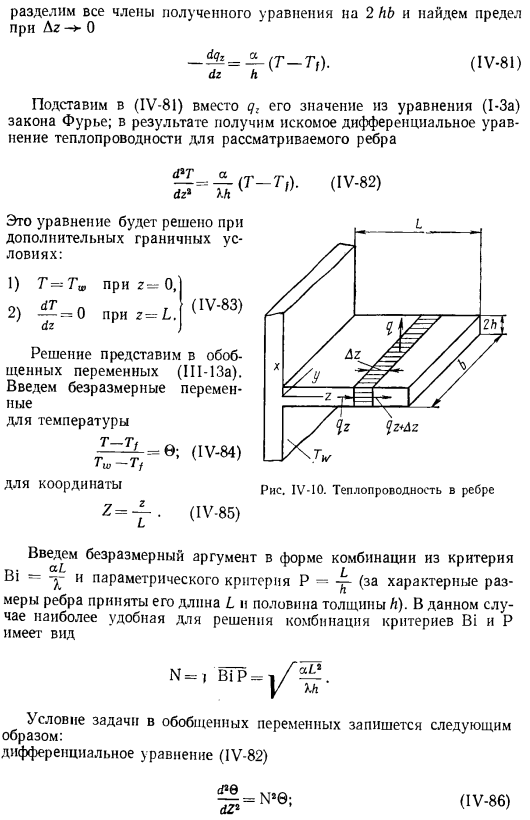
Кроме того, для усиления теплопередачи поверхность стенки со стороны газа увеличена ребрами. Рассмотрим теплопроводность некоторой кромки Раздел 1112).Упростите фактический процесс и предположите следующее: 1)температура ребра T изменяется только вдоль оси Z. 2) тепло передается только в окружающую среду Верхняя (Lb) и нижняя (Lb) поверхности ребра. 3) коэффициент передачи тепла от края нервюры к окружающей среде a постоянн значение, и поток тепла Формула = a (T-T.), (IV-80), где Tf-температура окружающей среды.

Выведем дифференциальное уравнение теплопроводности для ribs. To для этого создадим уравнение теплового равновесия выделенного объема qz2hb-qz + bz2hb-a (2b & z) (T-Tj)= ребро в виде 0 (рисунок IV-10).Разделите все члены полученного уравнения на 2 hb и найдите ограничение Az O (IV-81) dz h. подставьте (IV-81) вместо q. Значение из уравнения закона Фурье (1-Za). в результате получаем искомое дифференциальное уравнение теплопроводности для рассматриваемого ребра dza.

Дополнительные граничные условия: 1) t = Tda (IV-83) решение z = O, z-L обозначается обобщенной переменной (III-13a).Введение температурных безразмерных параметров (IV-84） ’W-координата 2 tf= -^ -. (IV-85) (IV-82) эталонный Bi = — y и параметрический эталонный P = — (для характерных размеров ребер、 Его длина L и половина толщины L). в этом случае наиболее удобное для решения сочетание критериев Bi и P принимает вид: условие задачи обобщенной переменной описывается следующим образом:.

Дифференциальные уравнения (IV-82) (IV-86) дополнительные граничные условия (IV-87) и решение системы br = o = 1 (IV-88) (IV-86, IV-87, IV-88) получены с помощью гиперболической функции в виде Или позвольте мне ввести характеристики эффективности реберной кости 8-NZ-(THN) sh NZ (IV-89) chN (l-Z) ch N (IV-90).Используйте отношение тепло которое на самом деле в качестве его меры Тепло, рассеиваемое поверхностью ребра, рассеивается, если температура всей поверхности ребра равна Tw. As в рассматриваемом случае и эффективность ребер Формула fOdZ-т — — — — — — — — — — — 5-L «1-г > I» (IV-91) о (IV-92) может быть определена.