Дифференциальное уравнение свободных колебаний тела подвешенного на пружине имеет вид (6 видео)

Дифференциальное уравнение свободных колебаний

Для изучения любого физического явления необходима модель. Моделью для изучения механических колебаний является гармонический осциллятор.

Гармоническим осциллятором называется система, совершающая колебания, которые могут быть описаны дифференциальным уравнением свободных гармонических колебаний, имеющим вид:

. (19.5)

Выражение (19.5) является линейным однородным дифференциальным уравнением второго порядка. Согласно общей теории линейных дифференциальных уравнений, решением уравнения (19.5) является выражение (19.1).

Колебания гармонического осциллятора являются важным примером периодического движения. Примерами гармонического осциллятора являются пружинный, математический и физический маятники.

Пружинный маятник — Пружинный маятник тело, подвешенное на пружине жесткостью k.Модель пружинного маятника показана на рис.19.1. Положение тела, при котором пружина не деформирована, является положением устойчивого равновесия. При отклонении тела от положения равновесия в результате деформации возникает сила упругости, которая согласно закону Гука равна .

Свободные колебания совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.

Дифференциальное уравнение свободных колебаний тела подвешенного на пружине имеет вид

Рис. 19.1

В случае пружинного маятника уравнение движения согласно второму закону Ньютона можно записать . Делим на m, получим:

. (19.6)

Учтем, что , получим уравнение (19.5)

Период колебаний пружинного маятника определяется как

. (19.7)

Потенциальная энергия пружинного маятника определяется как:

. (19.8)

Математический маятник. Математическим маятником называют подвешенный на тонкой нерастяжимой нити груз, размеры которого меньше длины нити, а масса больше массы нити.

Положение, в котором нить вертикальна – положение устойчивого равновесия. В положении устойчивого равновесия сила тяжести уравновешена силой натяжения нити , как показано на рис.19.2. При отклонении нити на угол α торавнодействующая сил тяжести и силы натяжения нити будет направлена к положению устойчивого равновесия.

. (19.9)

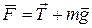
Если тело отпустить, то будем наблюдать свободные колебания. Во время колебаний можно считать, что меняется только координата х. Запишем проекцию равнодействующей силы на ось х

. (19.10)

При малых значениях a (a

4 о ) пренебрегаем движением вдоль оси y

(19.11)

Рис.19.2.

Из уравнения (19.10), учитывая (19.11) определим проекцию равнодействующей силы на ось х, которая согласно второму закону Ньютона равна

учтем, что , получим

Уравнение гармонических колебаний математического маятника можно записать в дифференциальной форме

. (19.12)

Подставим значение 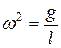. Получим уравнение (19.5). Отсюда период математического маятника равен

, (19.13)

где l – длина математического маятника.

Физический маятник. Физический маятник – твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, не проходящей через центр масс. Ось вращения, которого, расположена выше центра масс (рис.19.3).

При колебаниях физического маятника, возникает вращающий момент 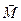, который согласно основному уравнению динамики вращательного движения равен:

, (19.14)

где J – момент инерции,

ε – угловое ускорение,

l – расстояние между точкой подвеса и центром масс. Уравнение (19.14) можно записать в виде: или .

Принимая во внимание или .

Можно получить выражение периода колебаний физического маятника:

, (19.15)

где — приведенная длина физического маятника. Приведенная длина, приравнивается длине математического маятника с таким же периодом колебаний.

Рис.19.3.

Период колебаний физического маятника, следовательно, и его приведенная длина, немонотонно зависят от расстояния от точки подвеса до центра масс маятника. Это легко заметить, если в соответствии с теоремой Штейнера (4.7) момент инерции выразить через момент инерции относительно параллельной горизонтальной оси, проходящей через центр масс. Тогда период колебаний будет равен

, (19.16)

где J₀ –момент инерции центра масс.

На практике значения низших собственных частот систем могут быть весьма малыми. Например, бельевая веревка, подвешенная на двух столбах, может в случае достаточного провисания совершать свободные колебания с частотой 1-2Гц. Колебания такого типа были обнаружены осенью 1959г. у проводов линии электропередачи, пересекавшей реку Северную, частота собственных колебаний была весьма низкой — около 1/8Гц. Провода диаметром 43мм, протянутые над рекой, были прикреплены к двум большим пилонам, расстояние между которыми превышало 1,6км. Было обнаружено, что когда ветер дул с небольшой силой, но в определенном направлении, возникали столь интенсивные низкочастотные колебания проводов, что эти провода, минимальное расстояние между которыми составляло 8,2м, входили в соприкосновение, вызывавшее короткое замыкание в системе электропередачи. (Была найдена вероятная причина этих колебаний, и в дальнейшем их удалось предотвращать путем покрытия тросов тонкой пластиковой лентой: благодаря этому изменялась геометрия поверхности, обтекаемой воздушным потоком).

Колебания проводов над рекой не представляют собой свободных колебаний, поскольку в этом случае пассивная система находилась под действием внешнего источника энергии — ветра. Однако характерно, что при решении этой проблемы инженерам, как обычно, потребовалась информация относительно значений собственных частот системы, близких к частоте наблюдавшихся колебаний.

18.3.Скорость и ускорение гармонических колебаний

Если материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат тогда зависимость координаты х от времени t описывается уравнением (19.1). Скорость и ускорение a колеблющееся точки соответственно равны:

, (19.17)

и , (19.18)

т.е. имеем гармонические колебания с той же циклической частотой. Амплитуды скорости и ускоренияколебаний соответственно равны υ_max = Аw и a_max= Аw₀ 2 . Фаза скорости (19.17) отличается от фазы величины (19.1) на , а фаза ускорения (19.18) отличается от фазы величины (19.1) на . В момент времени, когда х=0скорость колеблющейся точки максимальна по величине и равна амплитуде скорости в моменты прохождения колеблющейся точки через положение равновесия. При максимальных смещениях (х =±А) скорость равна нулю. Вектор скорости всегда направлен в сторону движения.

Ускорение равно нулю при прохождении колеблющейся точки через положение равновесия и достигает максимального по величине значения, которое равно амплитуде ускорения, при максимальных смещениях колеблющейся точки. Вектор ускорения всегда направлен в сторону положения равновесия. Удаляясь от положения равновесия, колеблющаяся точка движется, замедлено, приближаясь к нему – ускоренно.

Рис.19.4.

График гармонического колебания, который описывается уравнением (19.1), скорость гармонического колебания, описываемая уравнением (19.17), и ускорение (19.18) показаны на рис.19.4. Видно, что смещение, скорость и ускорение гармонически колеблющейся точки являются периодическими функциями от времени с одинаковыми периодами.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Дифференциальное уравнение свободных колебаний тела подвешенного на пружине имеет вид

Глава 13. Динамика точки.

13.4. Свободные незатухающие колебания.

13.4.1. Груз массой m = 25 кг подвешен к пружине с коэффициентом жесткости с = 800 Н/м и находится в свободном прямолинейном вертикальном колебательном движении. Определить модуль ускорения груза в момент времени, когда центр тяжести груза находится на расстоянии 5 см от положения статического равновесия. (Ответ 1,6)

13.4.2. Груз массой m = 20 кг подвешен к пружине с коэффициентом жесткости с = 400 Н/м и находится в свободном прямолинейном вертикальном колебательном движении. Определить, на каком расстоянии от положения статического равновесия находится центр тяжести груза в момент времени, когда его ускорение равно 3 м/с. (Ответ 0,15)

13.4.3. Определить приведенный коэффициент жесткости в Н/см двух последовательно соединенных пружин с коэффициентами жесткости с₁ = 2 Н/см и с₂ = 18 Н/см. (Ответ 1,8)

13.4.4. Коэффициенты жесткости пружин с₁ = 2 Н/м, с₂ = 4 Н/м и с₃ = 6 Н/м. Определить коэффициент жесткости пружинной подвески. (Ответ 1,09)

13.4.5. Дифференциальное уравнение колебательного движения груза массой m = 0,5 кг, подвешенного к пружине, имеет вид у + 60у = 0. Определить коэффициент жесткости пружины. (Ответ 30)

13.4.6. Определить максимальное удлинение пружины АВ в см при свободных вертикальных колебаниях груза, если он прикреплен в точке В к недеформированной пружине и отпускается из состояния покоя. Статическая деформация пружины под действием груза равна 2 см.
(Ответ 4)

13.4.7. Тело массой m = 10 кг подвешено к пружине и совершает свободные вертикальные колебания с периодом Т = 0,8 с. Определить коэффициент жесткости пружины. (Ответ 617)

13.4.8. Материальная точка массой m = 5 кг подвешена к пружине и находится в свободном вертикальном колебательном движении, закон которого задан графиком функции х = x(t). Определить коэффициент жесткости пружины. (Ответ 548)

13.4.9. Определить период свободных вертикальных колебаний груза массой m = 80 кг, который прикреплен к пружине с коэффициентом жесткости с = 2 кН/м. (Ответ 1,26)

13.4.10. Определить период свободных вертикальных колебаний тела, подвешенного к пружине, если статическая деформация пружины λ = 20 см. (Ответ 0,897)

13.4.11. Тело подвешено к пружине и совершает свободные вертикальные колебания с периодом Т = 0,5 с. Определить массу точки, если коэффициент жесткости пружины с = 200 Н/м (Ответ 1,27)

13.4.12. Тело, подвешенное к пружине, совершает свободные вертикальные колебания, заданные графиком функции у = у(t). Определить массу тела, если коэффициент жесткости пружины с = 300 H/м. (Ответ 122)

13.4.13. Период свободных вертикальных колебаний груза, подвешенного на пружине с коэффициентом жесткости с = 2 кН/м, равен Т = πс. Определить массу груза. (Ответ 500)

13.4.14. Дифференциальное уравнение колебательного движения груза, подвешенного к пружине, имеет вид х + 20х = 0. Определить массу груза, если коэффициент жесткости пружины с = 150 Н/м. (Ответ 7,5)

Видео:Колебательное движение. Свободные колебания | Физика 9 класс #23 | ИнфоурокСкачать

Свободные колебания пружинного маятника. Общие сведения

Цель работы. Ознакомиться с основными характеристиками незатухающих и затухающих свободных механических колебаний.

Задача. Определить период собственных колебаний пружинного маятника; проверить линейность зависимости квадрата периода от массы; определить жесткость пружины; определить период затухающих колебаний и логарифмический декремент затухания пружинного маятника.

Приборы и принадлежности. Штатив со шкалой, пружина, набор грузов различной массы, сосуд с водой, секундомер.

1. Свободные колебания пружинного маятника. Общие сведения

Колебаниями называются процессы, в которых периодически изменяется одна или несколько физических величин, описывающих эти процессы. Колебания могут быть описаны различными периодическими функциями времени. Простейшими колебаниями являются гармонические колебания – такие колебания, при которых колеблющаяся величина (например, смещение груза на пружине) изменяется со временем по закону косинуса или синуса. Колебания, возникающие после действия на систему внешней кратковременной силы, называются свободными.

Рассмотрим одну из простейших колебательных систем – пружинный маятник, представляющий собой груз массой m, подвешенный на абсолютно упругой пружине с коэффициентом жесткости k
(рис. 1). Пусть l0 – длина пружины без подвешенного к ней груза. При подвешивании груза под действием силы тяжести пружина растянется на x1 так, что маятник будет находиться в положении равновесия вследствие равенства модулей силы тяжести mg и упругой силы Fупр: mg = kx1, стремящейся вернуть груз в положение равновесия (полагается, что деформации пружины идеально упругие и подчиняются закону Гука).

Если груз вывести из положения равновесия, отклонив на величину x, то сила упругости возрастает: Fупр = – kx2= – k(x1 + x). Дойдя до положения равновесия, груз будет обладать отличной от нуля скоростью и пройдет положение равновесия по инерции. По мере дальнейшего движения будет увеличиваться отклонение от положения равновесия, что приведет к возрастанию силы упругости, и процесс повторится в обратном направлении. Таким образом, колебательное движение системы обусловлено двумя причинами: 1) стремлением тела вернуться в положении равновесия и 2) инерцией, не позволяющей телу мгновенно остановиться в положении равновесия. В отсутствии сил трения колебания продолжались бы сколь угодно долго. Наличие силы трения приводит к тому, что часть энергии колебаний переходит во внутреннюю энергию и колебания постепенно затухают. Такие колебания называются затухающими.

Незатухающие свободные колебания

Сначала рассмотрим колебания пружинного маятника, на который не действуют силы трения – незатухающие свободные колебания. Согласно второму закону Ньютона c учетом знаков проекций на ось X

(1)

Из условия равновесия смещение, вызываемое силой тяжести: . Подставляя в уравнение (1), получим: . Разделив правую и левую часть этого уравнения на m и принимая, что a = d2x/dt2, получим дифференциальное уравнение

. (2)

Это уравнение называется дифференциальным уравнением гармонических колебаний пружинного маятника. Из этого уравнения следует, что после прекращения внешнего воздействия, приводящего к первоначальному отклонению системы от положения равновесия, движение груза обусловлено только действием упругой силы (сила тяжести вызывает постоянное смещение).

Общее решение однородного дифференциального уравнения второго порядка (2) имеет вид

. (3)

Данное уравнение называется уравнением гармонических колебаний. Наибольшее отклонение груза от положения равновесия А0 называется амплитудой колебаний. Величина , стоящая в аргументе косинуса, называется фазой колебания. Постоянная φ0 представляет собой значение фазы в начальный момент времени (t = 0) и называется начальной фазой колебаний. Величина

(4)

есть круговая или циклическая частота собственных колебаний, связанная с периодом колебаний Т соотношением . Период колебаний определяется

. (5)

Рассмотрим свободные колебания пружинного маятника при наличии силы трения (затухающие колебания). В простейшем и вместе с тем наиболее часто встречающемся случае сила трения пропорциональна скорости υ движения:

где r – постоянная, называемая коэффициентом сопротивления. Знак минус показывает, что сила трения и скорость имеют противоположные направления. Уравнение второго закона Ньютона в проекции на ось Х при наличии упругой силы и силы трения

Данное дифференциальное уравнение с учетом υ = dx/dt можно записать

, (8)

где – коэффициент затухания; – циклическая частота свободных незатухающих колебаний данной колебательной системы, т. е. при отсутствии потерь энергии (β = 0). Уравнение (8) называют дифференциальным уравнением затухающих колебаний.

Чтобы получить зависимость смещения x от времени t, необходимо решить дифференциальное уравнение (8). В случае малых затуханий () решение уравнения можно записать следующим образом:

, (9)

где А0 и φ0 – начальная амплитуда и начальная фаза колебаний;
– циклическая частота затухающих колебаний при ω >> ω ≈ ω0.

Движение груза в этом случае можно рассматривать как гармоническое колебание с частотой ω и переменной амплитудой, меняющейся по закону:

. (10)

На графике функции (9), рис. 2, пунктирными линиями показано изменение амплитуды (10) затухающих колебаний.

Рис. 2. Зависимость смещения х груза от времени t при наличии силы трения

Для количественной характеристики степени затухания колебаний вводят величину, равную отношению амплитуд, отличающихся на период, и называемую декрементом затухания:

. (11)

Часто используют натуральный логарифм этой величины. Такой параметр называется логарифмическим декрементом затухания:

. (12)

Если за время t‘ амплитуда уменьшается в n раз, то из уравнения (10) следует, что

. (13)

Отсюда для логарифмического декремента получаем выражение

. (14)

Если за время t‘ амплитуда уменьшается в е раз (е = 2,71 – основание натурального логарифма), то система успеет совершить число колебаний

. (15)

Следовательно, логарифмический декремент затухания – величина, обратная числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз. Чем больше θ, тем быстрее происходит затухание колебаний.

2. Методика эксперимента и экспериментальная установка

Рис. 3. Схема установки

Установка состоит из штатива 1 с измерительной шкалой 2. К штативу на пружине 3 подвешиваются грузы 4 различной массы. При изучении затухающих колебаний в задании 2 для усиления затухания используется кольцо 5, которое помещается в прозрачный сосуд 6 с водой.

В задании 1 (выполняется без сосуда с водой и кольца) в первом приближении затуханием колебаний можно пренебречь и считать гармоническими. Как следует из формулы (5) для гармонических колебаний зависимость T 2 = f (m) – линейная, из которой можно определить коэффициент жесткости пружины k по формуле

, (16)

где – угловой коэффициент наклона прямой T 2 от m.

Задание 1. Определение зависимости периода собственных колебаний пружинного маятника от массы груза.

1. Определить период колебаний пружинного маятника при различных значениях массы груза m. Для этого с помощью секундомера для каждого значения m трижды измерить время t полных n колебаний (n ≥10) и по среднему значению времени вычислить период . Результаты занести в табл. 1.

2. По результатам измерений построить график зависимости квадрата периода T2 от массы m. Из углового коэффициента графика определить жесткость пружины k по формуле (16).

Результаты измерений для определения периода собственных колебаний

, с