Дифференциальное уравнение состояния объекта управления

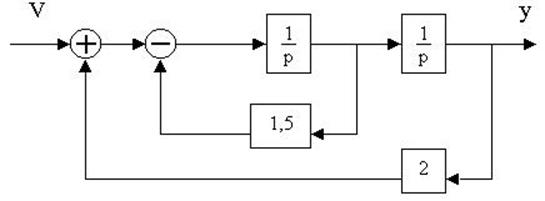
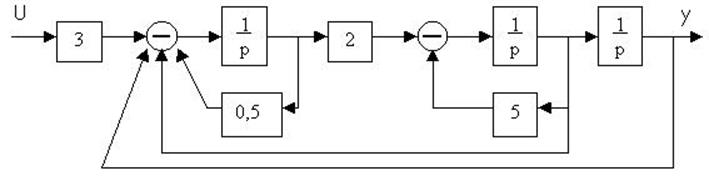
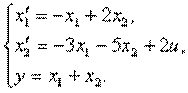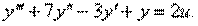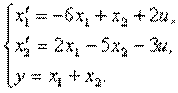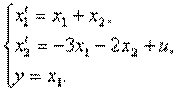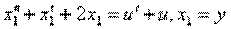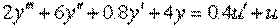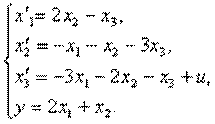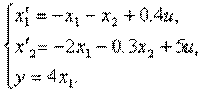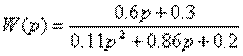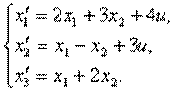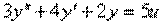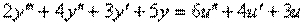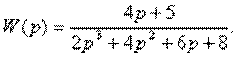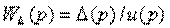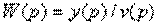При решении некоторых задач теории автоматического управления удобнее представлять дифференциальное уравнение объекта (5.1) или дифференциальные уравнения системы (5.4) и (5.6) в виде совокупности дифференциальных уравнений первого порядка. Не умаляя общности, рассмотрим эти уравнения применительно к управляемому объекту.

Пусть объект описывается дифференциальным уравнением n-го порядка (5.1)

называемых переменными состояния и представим уравнение (5.70) в виде системы дифференциальных уравнений

устанавливается алгебраическим уравнением

Обычно уравнения (5.71) и (5.72) записываются в векторпо-матричной форме:

— матрицы-столбцы. Матрицу-столбец-

могут иметь неодинаковые размерности.

В выборе переменных состояния имеется определенная свобода. Важно только, чтобы они были независимыми. От того, как выбраны переменные, зависит форма уравнений (5.73) и (5.74), т. е. вид входящих в них матриц.

При нормальной форме уравнений состояния в качестве переменных состояния выбираются сама управляемая величина п- 1 ее производные:

т. с. когда оно имеет вид

Достоинством нормальной формы является то, что переменные состояния имеют ясный физический смысл, а некоторые из них (например, хих2 и х:]) могут быть непосредственно измерены датчиками различных типов.

Для получения уравнений состояния в канонической форме уравнение объекта (5.70) представляется в виде

Если корни рь Ръ-Рп полинома С0(р) действительные однократные, то правая часть (5.80) может быть представлена в виде суммы элементарных дробей:

где К; и ()г- — коэффициенты разложения.

В качестве неременных состояния выбираются слагаемые суммы (5.81):

Большим достоинством канонической формы является диагоиальиость матрицы Л , что существенно упрощает решение уравнения (5.73). Основной недостаток ее состоит в том, что переменные состояния не имеют ясного физического смысла, в результате чего возникает проблема их непосредственного измерения.

Существуют и другие способы выбора переменных состояния, которые здесь не рассматриваются.

Решение векторно-матричиого уравнения (5.73) может быть представлено в виде

Здесь оно без строгого доказательства построено по аналогии с решением линейного дифференциального уравнения 1-го порядка

общий интеграл которого, как известно, определяется но формуле

называется переходной или фундаментальной матрицей. Если уравнения состояния представлены в канонической форме, то матрица А диагональная и имеет вид (5.85). Тогда

При других формах уравнений состояния для определения фундаментальной матрицы можно использовать известные способы нахождения матричных функций, например, теоремы Кели—Гамильтона или Сильвестра. Можно также использовать формулу

—

При необходимости можно осуществить обратный переход от уравнений состояния к передаточным функциям объекта. Для этого уравнение (5.73) запишем в изображениях по Лапласу:

получается формула (5.88). Из уравнения

(5.74) с учетом (5.89) найдем изображение управляемой величины при нулевых начальных значениях:

При описании свойств объекта уравнениями состояния возникают две проблемы, нетипичные для случая, когда используется одно дифференциальное уравнение я-то порядка. Эти проблемы рассматриваются в следующем параграфе.

Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Дифференциальное уравнение состояния объекта управления

Автор: Б.Т. Федосов

Видео:Теория автоматического регулирования. Лекция 5. Модели параметров состоянийСкачать

Уравнения состояния динамических объектов с запаздыванием

Проведено обобщение записи уравнений состояния на нелинейные многомерные динамические объекты и системы управления, имеющие протяжение в пространстве и элементы транспортного запаздывания. Обобщение осуществлено путем включения звеньев запаздывания, наряду с интеграторами, в состав простейших динамических, т.е. таких, выходные величины которых трактуются как самостоятельные переменные состояния.

1. Инерционные динамические объекты

Традиционное математическое описание динамического объекта в переменных состояния включает векторное уравнение состояния, связывающее скорости изменения переменных состояния с воздействиями на объект и значениями самих переменных состояния, а также векторное уравнение, связывающее значения выходных величин объекта (или результатов их измерений) с его переменными состояния и воздействиями на него [1 — 9]:

• где
• x – вектор переменных состояния;
• u – вектор воздействий на объект;
• y – вектор выходных величин объекта;
• z – вектор помех;
• f(.) и g(.) – некоторые, довольно общего вида функции.

Система (К.1.1) — это система векторных дифференциально-алгебраических уравнений переменных состояния многомерного нестационарного сосредоточенного в пространстве (точечного) нелинейного инерционно-динамического объекта управления.

Из уравнений (К.1.1) нетрудно видеть, что описание динамического объекта без запаздываний структурно содержит всего три типа операторов: линейный дифференцирующий (собственно динамический, инерционный) и два безинерционных нелинейных: элемент связи и элемент композиции:

Линейный дифференцирующий оператор описывает инерцию потому, что задает мгновенную скорость изменения переменной состояния, а, следовательно, определяет значение известной на текущий момент переменной на некоторый, пусть небольшой интервал времени вперед. Это и следует трактовать как инерцию, т.е. некоторую предопределенность поведения.

Рис. К.1.1. Описание инерционного объекта и его структурная модель. Дифференциальное уравнение, отражает причинно–следственную связь воздействия х и реакции (отклика) y простейшего инерционного звена: воздействие х приводит к изменению выходной величины y такому, что скоростьэтого изменения прямо пропорциональна воздействию. Интегратор – модель простейшего, фундаментального динамического (инерционного) элемента. Структурная модель отображает то, как причина, воздействие, преобразуется в следствие, выходную величину: модель простейшей (фундаментальной) инерционности обеспечивает накопление и сохранение воздействия

В линеаризованной модели объекта справедлив принцип суперпозиции и поэтому оператор композиции переменных представляет собой их взвешенную сумму, а оператор связи становится линейным:

Уравнения динамического объекта в переменных состояния можно представить и в интегральном виде, более наглядном для структурного моделирования:

Уравнение состояния описывает собственную, внутреннюю инерционность динамического объекта. Уравнение выхода учитывает помехи измерению компонент вектора выходных величин.

Состояние и тенденция поведения хотя бы на бесконечно малый интервал вперед чисто инерционного динамического объекта определяется набором значений всех переменных состояния объекта в некоторый момент времени и отображается соответствующим положением изображающей точки в многомерном пространстве состояний. Поскольку эта информация для инерционного объекта без запаздывания исчерпывающая, то координаты любой точки траектории изображающей точки могут рассматриваться как начальные условия для интегрирования уравнений состояния, т.е. для определения всей последующей траектории движения изображающей точки, оценке поведения динамического объекта под внешними воздействиями или в отсутствие таковых.

В качестве иллюстрации этого приведем фазовые портреты (траектории движения изображающих точек объектов в двумерном пространстве состояний) для модели свободной колебательной системы с отличающимися начальными условиями:

Рис. К.1.1. Фазовые портреты свободной инерционной колебательной системы при разных начальных условиях, соответствующих одной и той же фазовой траектории совпадают, т.е. координаты любой точки фазовой траектории могут рассматриваться как начальные условия, полностью определяющие дальнейшее свободное поведение объекта

Таким образом, поведение точечных (исключительно инерционных, не имеющих элементов запаздывания) динамических объектов полностью описывается уравнениями состояния и выхода, а также начальными условиями, представляющими собой значения всех переменных состояния объекта в некоторый момент времени, и отображается некоторой траекторией, а текущее состояние объекта характеризуется точкой в многомерном пространстве переменных состояния.

2. Уравнения состояния протяженных объектов с элементами запаздывания

Учет звеньев запаздывания в моделях объектов как второго, самостоятельного вида простейших динамических элементов, наряду с инерционными (интеграторами), позволяет единообразно описывать в переменных состояния динамические объекты практически любой сложности и на этой основе проводить их анализ и оптимизацию.

2.1. Уравнения и структура моделей протяженных динамических объектов

Дифференциальная форма уравнений состояния протяженного объекта

Наличие элементов задержки в некоторых ветвях модели динамического объекта существенно, а часто и принципиально, изменяет динамические свойства объекта по сравнению с объектом без элементов запаздывания. Поэтому пространство состояний соответствующих только выходным величинам инерционных элементов (интеграторов) не в полной мере задает состояние и поведение объекта, имеющего звенья запаздывания.

Элемент запаздывания динамического объекта, также, как и инерционный, следует рассматривать как динамический, а его выходную величину – как отдельную переменную состояния.

Основание для отнесения звена задерживающего сигнал на конечный интервал времени к элементарным динамическим опирается на сходство и различия двух видов простейших динамических элементов моделей реальных объектов и состоит в следующем.

Внешнее отличие состоит в том, что инерционный элемент описывается элементарным дифференциальным уравнением, в то время как запаздывающий – алгебраическим.

Термин «динамический» относят к объектам, поведение которых под внешним воздействием можно предсказать хотя бы на бесконечно малый интервал. Инерционный элемент, интегратор, традиционно считающийся единственным динамическим, такому требованию отвечает. Но этому же требованию отвечает и звено запаздывания, если известна предыстория воздействия на него. В таком случает звено запаздывания позволяет жестко определить поведение его выходной величины на конечный интервал времени вперед. Т.о. звено запаздывания может быть отнесено к динамическим.

С другой стороны, звено запаздывания соответствует в реальных объектах либо переносу материалов («транспортное запаздывание»), либо задержке поступления сигнала (модели воздействия) на вход некоторого элемента объекта, связанной с распространением его в пространстве. Таким образом, звено запаздывания может быть отнесено и к элементам связи.

Нестационарный элемент запаздывания, обладающий дисперсией, и его частный случай, элемент чистой задержки, также как и простейший инерционный элемент является динамическим потому, что его выходной сигнал своеобразен, не может быть получен безинерционной композицией других, только инерционных переменных состояния. Это результат задержки по времени такой композиции.

Для обобщения уравнений состояния точечных объектов, представленных в форме Коши, на протяженные объекты и объекты с транспортным запаздыванием формально введем оператор прогнозирования Fwd [7]:

Этот оператор в общем случае, естественно, физически не реализуем, поскольку должен абсолютно точно предсказывать значение переменной, на которую он воздействует, на конечный интервал τ времени вперед. Но этот оператор нужен всего лишь для формального «красивого» исходного представления уравнений состояния, а их структурное решение возможно с использованием реализуемого оператора запаздывания. С другой стороны, оператор прогнозирования в уравнениях состояния действует только на переменную состояния такую, значения которой определяются предысторией поведения всех переменных состояния объекта с запаздыванием и входных воздействий, т.е. некоторой композиции таковых, и поэтому, в этом частном случае, он реализуем, поскольку прогноз жестко определяется предысторией.

Итак, запишем векторные уравнения переменных состояния протяженного динамического объекта в виде:

В (К.2.1.2) для удобства записи и чтения переменные состояния разделены на две группы. Переменные x₍₁₎ первой группы это переменные состояния простейших инерционных элементов объекта, их выходные величины. Переменные x₍₂₎ это переменные состояния, соответствующие выходам звеньев запаздывания объекта. Очевидно, что в принципе, «инерционные» и «запаздывающие» переменные состояния могут быть записаны и пронумерованы и в произвольном порядке и объединены в одном векторном уравнении.

Отметим, что обобщенная система уравнений состояния динамического объекта имеет только одну независимую переменную – время t. Пространственные же характеристики объекта в (К.2.1.2) описываются косвенно, путем учета вектора времен задержек τ, обусловленных распространением воздействий в пространстве с конечной (не бесконечной) скоростью или транспортным запаздыванием.

Рассмотрение динамических объектов с запаздыванием на основе описания их уравнениями состояния проводилось некоторыми авторами и ранее [8, 10, 11].

В [8] п. 2.1, (2.1.2), описание ограничивается указанием на задержки только в правых частях уравнений и не включает звенья запаздывания в структуру модели в качестве функционирующих элементов, определяемых собственными переменными состояния. Похожее исходное представление уравнений состояния используется и в [10], «1.5. Оптимальное управление системами с транспортным запаздыванием», стр.188 и далее, а также в [11].

Форма уравнений (К.2.1.2) отличается от предложенной в [8, п. 2.1, (2.1.2)] введением специальных переменных состояния, соответствующих выходным величинам звеньев запаздывания. Этим самым звенья запаздывания отнесены с простейшим динамическим и описание динамических объектов становится универсальным.

В предлагаемом в настоящей статье представлении динамического объекта текущее внутреннее состояние объекта полностью определяется вектором значений переменных состояния, соответствующих выходным величинам интеграторов и звеньев запаздывания, и предысторией их поведения.

Интегральная форма уравнений состояния протяженного объекта

Уравнения переменных состояния динамического объекта с запаздыванием могут быть представлены в интегрально–«запаздывающей» форме, которая, пожалуй, является более наглядной для составления структурной модели объекта:

где операторы задержки:

осуществляют обратное по действию по отношению к оператору прогноза Fwd .

Итак, (К.2.1.3) – интегрально–«запаздывающие» уравнения векторных переменных состояния многомерного протяженного нелинейного нестационарного динамического объекта. Часть переменных, соответствующая выходным сигналам простейших инерционных элементов и обозначенная вектором x₍₁₎, есть результат накопления (интегрирования) некоторой комбинации всех переменных, которая, как и сами переменные, а также входные воздействия, может изменяться с течением времени. Вторая часть переменных состояния, обозначенная x₍₂₎, представляет собой задержку некоторой комбинации всех переменных состояния, а также и входных воздействий объекта, на некоторое время τ (вектор), которое может в общем случае меняться с течением времени. В соответствии с этими уравнениями могут быть построены структурные, в т.ч. виртуально–аналоговые, модели динамических объектов [7].

Начальные условия уравнений состояния протяженного объекта

В уравнениях (К.2.1.3) начальные условия для звеньев (операторов) задержки это не просто значения комбинаций переменных состояния и входных воздействий в нулевой момент времени, как это имеет место для интеграторов. Для однозначного решения уравнений (К.2.1.3) требуется задать начальные условия для звеньев запаздывания в виде функций, определяющих историю поведения входных величин этих звеньев на тот интервал времени назад, на который они осуществляют задержку.

Т.о. звенья запаздывания, обладая «памятью», требуют больше информации для однозначного решения вопроса о поведении объекта: не просто вектор значений переменных состояния в некоторый, условно нулевой момент времени, как этого достаточно для интеграторов, но вектор функций (комбинаций переменных состояния и входных воздействий на объект), заданных на соответствующих звеньям запаздывания временных интервалах, предшествующих началу интегрирования.

Другими словами, состояние и поведение динамического объекта, как точки и траектории в пространстве состояний для систем с запаздыванием определяется не только положением точки в этом пространстве, но и ее предыдущей траекторий как в подпространстве «запаздываний» x(₂), так и в подпространстве x(₁) «инерционных» переменных, а также историей поведения внешних воздействий в течение тех интервалов времени, на которые происходит задержка в соответствующих звеньях запаздывания.

Аналогичное утверждение для традиционной формы представления уравнений состояния объектов с запаздыванием приводится и в [8] п. 2.1:

«Состояние непрерывного объекта с запаздыванием в произвольный момент времени характеризуется не только некоторым конечным числом параметров (имеются в виду переменные состояния – Ф.Б.Т.) (как в случае объектов без запаздывания), но и некоторыми функциями, определенными соответственно на интервале [t₀ – τ_e, t₀], [t₀ – θ_r, t₀]. Это значительно усложняет решение задач управления такими объектами».

Вообще говоря, проблема задания начальных условий для звеньев запаздывания свойственна не только описанию динамического объекта в переменных состояния, но и для других методов описания. Часто при цифровом моделировании динамических объектов с запаздыванием принимают начальную траекторию «запаздывающих» переменных, т.е. выходных величин звеньев запаздывания постоянной. Для этого буфер звена заполняется в исходном состоянии нулями или константой.

Входной сигнал звена запаздывания, входящего в состав динамического объекта, представляет собой композицию переменных состояния, относящихся к другим звеньям, и воздействий на объект, поэтому задание жесткого прогноза изменения выходного сигнала звена запаздывания эквивалентно заданию предыстории поведения названных переменных состояния и воздействий на тот же интервал времени.

Рис. 2.1.1. Состояние динамического объекта с запаздыванием в некоторый момент времени характеризуется положением его изображающей точки в пространстве состояний, координатами которой являются значения переменных состояния в этот момент времени, а также траекторией этой точки в предшествующие текущему моменты времени. Многомерное пространство состояния можно представить в виде совокупности подпространства инерционных переменных состояния и подпространства «задержанных» переменных состояния

Таким образом, для точечных объектов положение изображающей точки в пространстве состояний в некоторый момент времени полностью определяет состояние динамического объекта и тенденцию его поведения в ближайшее время. Для объектов, протяженных в пространстве, имеющих в своей структуре звенья транспортного запаздывания, их состояние и последующее поведение определяется не только текущим положением изображающей точки, но и траекторией ее движения в пространстве состояний в предшествующий, может быть достаточно большой, интервал времени.

Структура модели динамического объекта с запаздываниями

Структура модели динамического объекта с запаздываниями, соответствующая системе (К.2.1.3) в укрупненном виде представлена на рисунке:

Рис. К.2.1.2. Укрупненное схематическое изображение основных структурных элементов модели наблюдаемого многомерного нестационарного протяженного в пространстве нелинейного динамического объекта управления. Собственные динамические свойства объекта определяются структурой, характеристиками и параметрами левого блока, блок преобразователя осуществляет преобразование переменных состояния в величины, которые могут быть измерены (или непосредственно в результаты измерений)

Рис. K.2.1.3. Структура модели собственно динамического объекта, отражающая его внутренний «метаболизм», т.е. направления передачи значений воздействий и переменных, а также операции, осуществляемые над ними. Поведение объекта с запаздыванием определяется не только вектором начальных условий «инерционных» переменных состояния, но и предысторией всех переменных состояния, а также и предысторией воздействий на объект

Сложный динамический объект с функциональными элементами запаздывания структурно представляется двумя параллельными контурами, инерционным и «запаздывающим». Переменные состояния всего объекта это объединение инерционных и «запаздывающих» переменных состояния (выходных величин простейших инерционных элементов в структуре объекта, и «запаздывающих», т.е. выходных величин звеньев запаздывания) в один вектор.

Как отмечалось выше, в общем случае, входной сигнал некоторого звена запаздывания определяется как всеми переменными состояния объекта, так и всеми воздействиями на него. Поэтому, для того, чтобы однозначно определить состояние, а затем и поведение объекта, необходимо знать значения и прогноз поведения «запаздывающих» переменных состояния, или, что эквивалентно, предысторию поведения всех переменных состояния и входных воздействий объекта.

2.2. Простейшие структурные элементы протяженных объектов

Как видно из уравнений (K.2.1.2) и (K.2.1.3) состояния и выхода динамических объектов с запаздыванием, для их описания достаточно всего четырех операторов. Математическое описание всех четырех простейших элементов (виртуальных аналогов этих операторов) динамических систем и объектов, имеющих пространственное протяжение и (или транспортное запаздывание), опосредованно опирающихся на физические законы их описывающие, сводится к простым уравнениям, одно из которых линейное дифференциальное, а три остальные – алгебраические:

• где
• х – воздействие на элемент,
• y – его реакция,
• t – время,
• τ – некоторая задержка во времени.

Рис. K.2.2.1. Интегратор и стационарное звено запаздывания – исчерпывающий набор видов элементарных динамических объектов. Эти простейшие динамические элементы моделей объектов с запаздыванием требуют для полного и однозначного описания состояния и поведения объекта задания начальных условий. Для интегратора это просто значение выходной величины в условный нулевой момент времени, для звена запаздывания «начальное» условие это поведение входной величины в предшествующие моменты времени на интервале [–τ, 0], или, что то же самое, прогноз поведения выходной величины звена запаздывания («запаздывающей» переменной состояния) на интервал [0, τ], равный времени задержки в звене

Рис. K.2.2.2. Простейшие (фундаментальные) элементы общего вида структурной схемы динамического объекта как его математической модели насчитывают только четыре разного типа элементов. Элементов этих типов достаточно для моделирования сколь угодно сложного динамического объекта (технологической установки, системы управления ей и т.п.)

Комбинируя простейшие элементы можно построить состоятельную модель сколь угодно сложного динамического объекта. Составление системы дифференциально–алгебраических уравнений динамического объекта в виде уравнений состояния это неявный, опосредованный способ, некое «таинство», представления модели динамического объекта в виде набора взаимодействующих между собой однонаправленных простейших динамических элементов.

2.3. Наблюдаемость и управляемость объектов с запаздыванием

Из проведенного выше рассмотрения следует, что однозначное состояние динамического объекта с запаздыванием определяется не только текущими значениями переменных состояния, но и историей их изменения в предыдущие моменты времени, на конечном и достаточно протяженном интервале. Поэтому для таких объектов следует уточнить понятия наблюдаемости и управляемости.

Управляемость динамического объекта с элементами запаздывания состоит в том, чтобы имелась возможность за конечное время конечным изменением вектора воздействий перевести объект из текущего состояния, которому предшествовало некоторое определенное поведение, в новое, требуемое состояние, которому предшествует заданная траектория изображающей точки в пространстве состояний.

Наблюдаемость объекта с запаздыванием определим как возможность нахождения текущего вектора переменных состояния в любой момент времени и конечный участок траектории в пространстве состояний, по которой изображающая точка попадает в текущее положение, по измерениям выходных величин объекта и их поведения в течение некоторого предшествующего интервала времени.

Более строгие определения понятий наблюдаемости и управляемости динамических объектов в представлении запаздываний в правых частях уравнений состояния можно посмотреть в [8]: «2.6. Управляемость и наблюдаемость систем с запаздыванием».

2.4. Состояние и начальные условия динамического объекта с запаздыванием

Текущее состояние динамического объекта с запаздыванием должно однозначно определять его поведение в последующие моменты времени, хотя бы на весьма короткий интервал. В отсутствие внешних воздействий на объект (свободное движение), или при известных внешних воздействиях, это время простирается до бесконечности.

Состояние динамического объекта с запаздыванием определяется мгновенным значением всех переменных состояния, «инерционных» и «запаздывающих», а также их предысторией и предысторией воздействий на объект.

Рис. К.2.4.1. Фазовые портреты и поведение переменных состояния динамического объекта с запаздыванием в отсутствие внешних воздействий. Если рассматривать звено с запаздыванием как элементарное динамическое, т.е. считать его выходную величину как самостоятельную переменную состояния, то для полного описания состояния и тенденции поведения динамического объекта с запаздыванием требуется задать не только значения переменных состояния в некоторый момент времени, но и предысторию их изменения, помещенную в данном случае в буфер звена запаздывания. Разные предыстории приводят к разным траекториям фазового портрета, т.е. к разному поведению объекта. Прогноз поведения выходной переменной звена запаздывания (переменной состояния х3) эквивалентен предыстории поведения его входной величины, поскольку представляет собой задержанную на время запаздывания, в данном случае τ = 1 сек, эту самую предысторию. Интервал, на котором следует знать предысторию определяется величиной задержки в звене запаздывания

Как видно, для задания начальных условий уравнений состояний, а также, что эквивалентно, для однозначного описания текущего состояния динамического объекта с запаздыванием необходимо знать не только значения переменных состояния, но и их предысторию.

Рис. K.2.4.2. Начальные условия, или что эквивалентно, состояние инерционно–динамических объектов и инерционно–динамических объектов с запаздыванием. Для чисто инерционного объекта для всестороннего описания его свойств достаточно знать значения всех переменных состояния в некоторый момент времени, а также, значения входных воздействий на объект, если таковые существуют. Объект с запаздываниями требует не только знания значений всех переменных состояния, как инерционных (выходных сигналов интеграторов модели), так и «запаздывающих» (выходных сигналов звеньев запаздывания модели), но и иметь прогноз поведения «запаздывающих»

Таким образом, для описания объектов с запаздыванием требуется значительно больше информации, чем для просто инерционных объектов, что усложняет их анализ и оптимизацию.

2.5. О полном пространстве состояний цифровой модели динамического объекта с запаздыванием и его состоятельном подпространстве

Модели реальных непрерывных инерционных динамических объектов без запаздывания могут быть построены как с использованием исключительно интеграторов (W(p) – модель), так и с использованием только элементарных звеньев запаздывания ( W(z)–модель):

Рис. 2.5.1. (анимация, 14 кадров) Модели инерционной колебательной системы, построенные на базе интеграторов и на базе элементарных звеньев запаздывания, осуществляющих задержку на один такт, эквивалентны, как это видно по переходным функциям выходных величин, х1 и z1 соответственно. Естественно, переменные состояния этих моделей, соответствующие выходным величинам интеграторов и звеньев задержки сигналов на такт моделирования разные. Поэтому и траектории изображающих точек разных пар переменных – разные. Конечно, у модели на элементарных звеньях запаздывания траектория изображающей точки довольно «скучная», идет по диагонали, поскольку обе переменные отличаются на незначительную величину, что принципиально важно для обеспечения состоятельности модели

Отметим, что интеграторами (апериодическими звеньями) нельзя даже приближенно промоделировать звенья с достаточно большим запаздыванием, в то время как любое запаздывание без проблем с любой точностью моделируется звеньями задержки на такт, достаточно только выбрать их достаточное число.

Рис. 2.5.2. Непрерывное звено запаздывания и его цифровые модели. Переменная состояния, несущая содержательную, исчерпывающую информацию это выходная величина звена запаздывания с учетом предыстории поведения его входного воздействия. Выходные сигналы промежуточных элементов дискретной модели звена запаздывания формально можно отнести к переменным состояния, однако, поскольку информация в них повторяется со сдвигом, достаточно ограничиться только выходной величиной всего звена и рассматривать его как элементарное унитарное динамическое, состояние которого определяется не только значением выходной величины, но и ее прогнозом (предысторией входной величины). Буфер унитарной дискретной модели заполнен предысторией входной величины, поэтому прогноз переменной состояния жестко определяется этой предысторией

Определение переменной состояния, отнесенной к звену запаздывания, собственно, равной последней величине микрозвеньев буфера запаздывания, позволяет использовать в качестве состоятельного подпространства состояний такое, которое включает только выходные величины элементарных звеньев, составляющих цифровую модель звена запаздывания. Относительно малое число эффективных переменных состояния особенно важно при аналитическом исследовании динамического объекта и графическом представлении его результатов.

Заключение

Звено запаздывания на конечную величину может рассматриваться в дополнение к интегратору как простейший динамический элемент, выходная величина которого является самостоятельной переменной состояния, причем для полного и однозначного описания состояния объекта необходимо знать как положение изображающей точки в пространстве состояний, так и часть ее предыдущей траектории, т.е предысторию поведения объекта.

Оптимальная система управления, если она уже реализована, существует объективно и ее характеристики не зависят от того, каким математическим аппаратом она была описана и с помощью каких математических методов и инструментов она была оптимизирована. Поэтому простота математического описания системы управления, в частности САР, должна определяться сложностью системы, ей соответствовать.

Литература и Интернет

• 1. Ким Д.П. Теория автоматического управления. Т.2. Многомерные, нелинейные, оптимальные и адаптивные системы: Учеб. Пособие. – М.: ФИЗМАТЛИТ, 2004. – 464 с. – ISBN 5–9221–0534–5.
• 2. Ким Д.П. Сборник задач по теории автоматического управления. Многомерные, нелинейные, оптимальные и адаптивные системы. – М.: ФИЗМАТЛИТ, 2008. – 328 с. – ISBN 978–5–9221–0937–6.
• 3. Yuan Yan. Automatic Control Theory. Chapter 1–9. Presentation, pdf–format. School of Information Science and Engineering, CSU. 28.8.2005
  http://wuhua.csu.edu.cn/ac/ac/ch1.pdf
  http://wuhua.csu.edu.cn/ac/ac/ch2.pdf
  .
  http://wuhua.csu.edu.cn/ac/ac/ch9.pdf
• 4. Лукас В.А. Теория управления техническими системами. Компактный учебный курс для вузов. – 3–е издание, перераб. и дополн. – Екатеринбург. Изд–во УГГА, 2002, – 675 с.
• 5. Д. Сю, А. Мейер. Современная теория автоматического управления и ее применение. Перевод с английского В. С. БОЧКОВА, Е. В. ГУРЕЦКОЙ, Л. М. КИСЕЛЕВОЙ и В. Г. ПОТЕМКИНА. Под редакцией д.т.н. профессора Ю. И. ТОПЧЕЕВА. –М., : МАШИНОСТРОЕНИЕ, 1972.
• 6. Дорф Р., Бишоп Р. Современные системы управления. Пер. с англ. Копылова Б.И. – М. :Лаборатория базовых знаний, С_Пб, 2002. –832 с. ISBN 5–93208–119–8
• 7. Федосов Б.Т. Многомерные объекты. Описание, анализ и управление. Рудный, 2010.
  http://model.exponenta.ru/bt/bt_171_MultyDim_Obj_Contr.htm
• 8. Ю.Ю. Громов и др. Системы автоматического управления с запаздыванием. –Тамбов. :Издательство ТГТУ, 2007.
  http://window.edu.ru/window_catalog/files/r56879/k_Gromov1.pdf (698 КБ)
• 9. Калман Рудольф Э., Фалб Питер Л., Арбиб Майкл А. Очерки по математической теории систем: Пер. с англ. / Под ред. Я.3.Цыпкина. Предисл. Э.Л.Наппельбаума. Изд. 2–е, стереотипное. — М.: Едиториал УРСС, 2004. – 400 с. ISBN 5–354–00762–3
  R.E.Kalman, R.L.Falb, M.A.Arbib
  Topics in mathematical system theory
• 10. Ф. Чаки. Современная теория управления. Нелинейные, оптимальные и адаптивные системы. Перевод с английского В. В. Капитоненко и С. А. Анисимова. Под редакцией Н. С. Райбмана М., : МИР 1975
• 11. В.М. Синеглазов, Р.Ю. Ткачев. Автономное управление многомерным объектом с запаздываниями общего вида. Кибернетика и вычисл. техника. Межведомственный сборник научных трудов. Вып. 157. Киев, 2009, с. 17 –25.

Благодарности

Автор выражает признательность к.т.н., доценту Клиначёву Н.В (ЮУрГТУ, Челябинск) и д.т.н., профессору Колесову Ю.Б. (С–ПбГПУ ,С–Петербург) за полезное обсуждение вопросов, рассматриваемых в статье.

Видео:Устойчивость 1 ОпределениеСкачать

Задачи и пример решения одной из них по теме «Структурный метод»

Страницы работы

Содержание работы

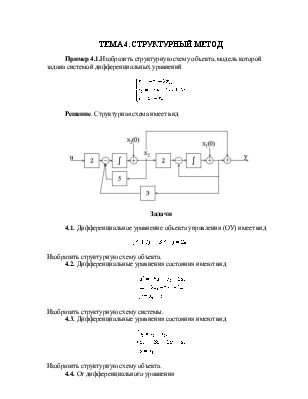
ТЕМА 4. СТРУКТУРНЫЙ МЕТОД

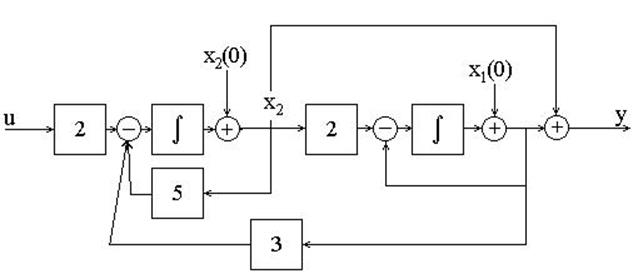
Пример 4.1.Изобразить структурную схему объекта, модель которой задана системой дифференциальных уравнений

Решение. Структурная схема имеет вид

4.1. Дифференциальное уравнение объекта управления (ОУ) имеет вид

Изобразить структурную схему объекта.

4.2. Дифференциальные уравнения состояния имеют вид

Изобразить структурную схему системы.

4.3. Дифференциальные уравнения состояния имеют вид

Изобразить структурную схему объекта.

4.4. От дифференциального уравнения

перейти к структурной схеме.

4.5. От дифференциального уравнения

описывающего объект, перейти к структурной схеме.

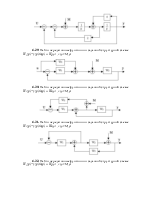
4.6. Изобразить структурную схему объекта, модель которого задана системой дифференциальных уравнений

4.7. Известна модель объекта в пространстве состояний

Изобразить структурную схему на интегрирующих элементах.

4.8. По известной передаточной функции объекта

записать дифференциальное уравнение и изобразить структурную схему.

4.9. Представить в виде структурной схемы модель ОУ, заданную системой дифференциальных уравнений

4.10. Представить в виде структурной схемы модель ОУ, заданную дифференциальным уравнением

4.11. Представить в виде структурной схемы модель ОУ, заданную дифференциальным уравнением

4.12. Перейти от передаточной функции к структурной схеме, содержащей только интеграторы, сумматоры и усилители

4.13. Перейти от передаточной функции W(p) к структурной схеме, содержащей только интеграторы, сумматоры и усилители, где

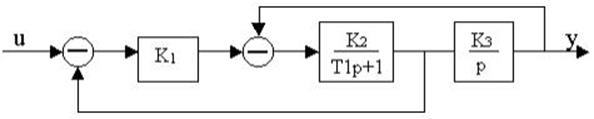
4.14. Структурная схема системы имеет вид

Определить передаточную функцию

4.15. Структурная схема системы имеет вид

Определить передаточную функцию системы.

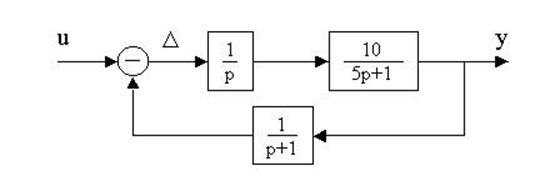
4.16. Определить W(p)=y(p)/u(p) по заданной структурной схеме и составить описание системы в пространстве состояний

4.17. По структурной схеме

определить W(p)=y(p)/u(p),составить описание в пространстве состояний.

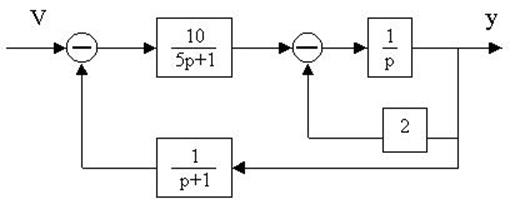
4.18. По структурной схеме определить передаточную функцию

4.19. Для заданной структурной схемы

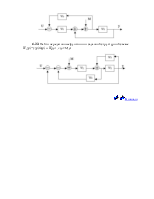
4.20. Структурная схема системы имеет вид

4.21.Структурная схема системы имеет вид

определить передаточную функцию W(p).

4.22.Структурная схема системы имеет вид

определить передаточную функцию W(p).

4.23.Структурная схема системы имеет вид

определить передаточную функцию W(p).

4.24.Структурная схема системы имеет вид

определить передаточную функцию W(p), записать дифференциальное уравнение относительно y, u.

4.25.Структурная схема системы имеет вид

определить передаточную функцию W(p).

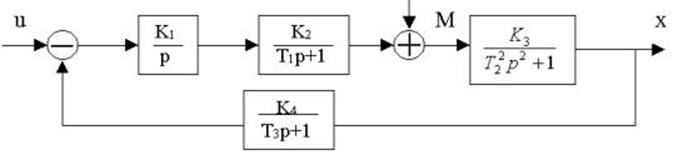
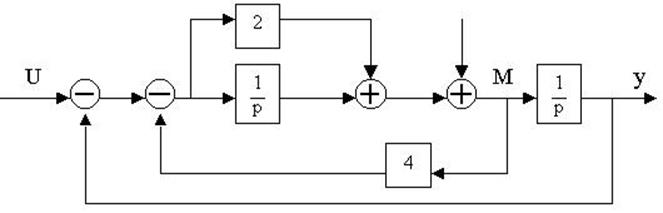
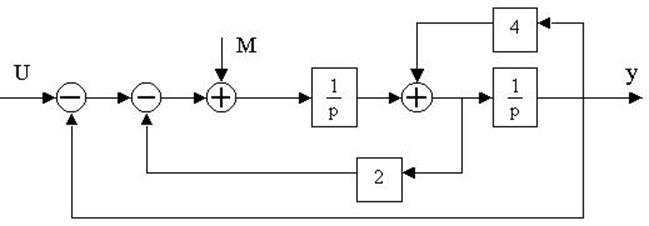
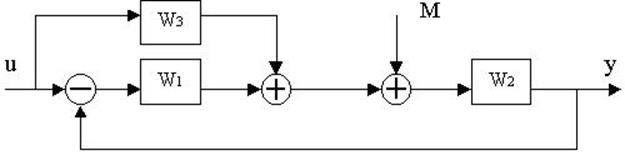
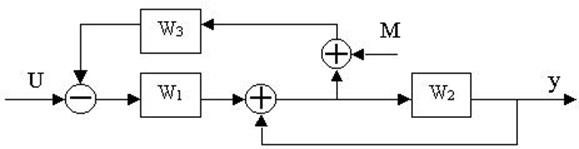
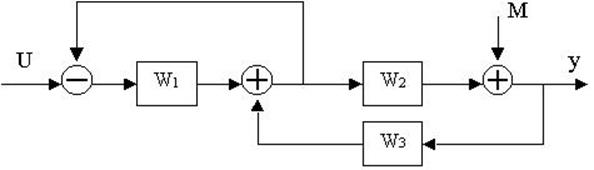
4.26. Для заданной структурной

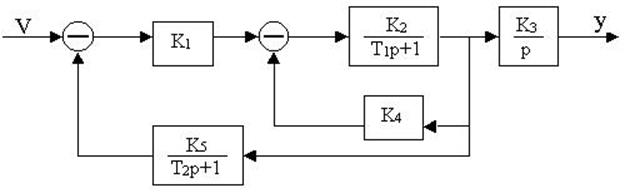
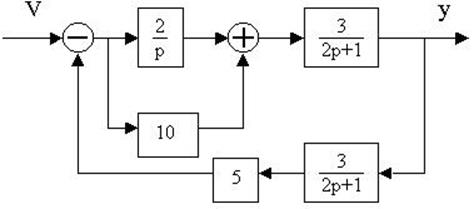
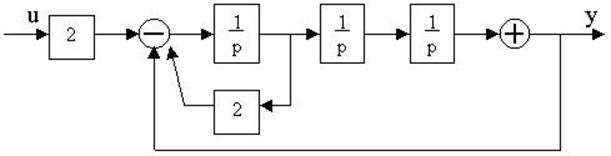
4.27. Найти передаточные функции по заданной структурной схеме W₁(p)=y(p)/u(p) и W₂(p)=y(p)/М(p)

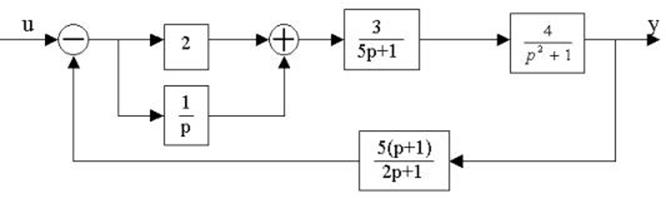
4.28. Найти передаточные функции по заданной структурной схеме W₁(p)=y(p)/u(p) и W₂(p)=y(p)/М(p)

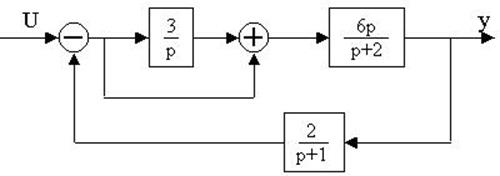
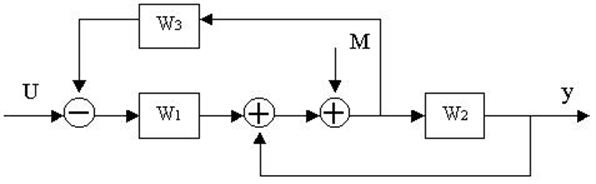
4.29. Найти передаточные функции по заданной структурной схеме W₁(p)=y(p)/u(p) и W₂(p)=y(p)/М(p)

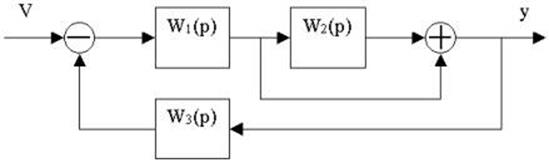
4.30. Найти передаточные функции по заданной структурной схеме W₁(p)=y(p)/u(p) и W₂(p)=y(p)/М(p)

4.31. Найти передаточные функции по заданной структурной схеме W₁(p)=y(p)/u(p) и W₂(p)=y(p)/М(p)

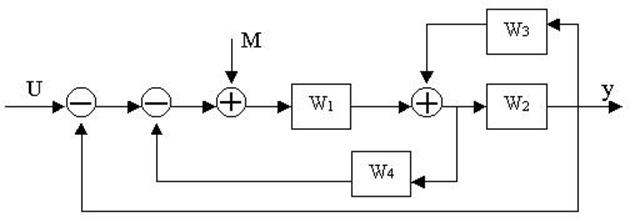
4.32. Найти передаточные функции по заданной структурной схеме W₁(p)=y(p)/u(p) и W₂(p)=y(p)/М(p)

4.33. Найти передаточные функции по заданной структурной схеме W₁(p)=y(p)/u(p) и W₂(p)=y(p)/М(p)

В начало

🎦 Видео

Метод пространства состояний САУ: описание конкретной системыСкачать

Дифференциальные уравнения. 11 класс.Скачать

Видеометодичка. Практикум по нахождению передаточных функций по дифференциальным уравнениямСкачать

Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Дифференциальные уравнения для самых маленькихСкачать

1. Что такое дифференциальное уравнение?Скачать

Дифференциальные уравнения для процессов различной физической природыСкачать

Математика это не ИсламСкачать

Дифференциальные уравнения в частных производных #calculus #mathsСкачать

ТАУ. Matlab/SIMULINK Фазовые портреты систем нелинейных диф. уравненийСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

2) ТАУ для чайников. Часть 2.1: Математические модели...Скачать