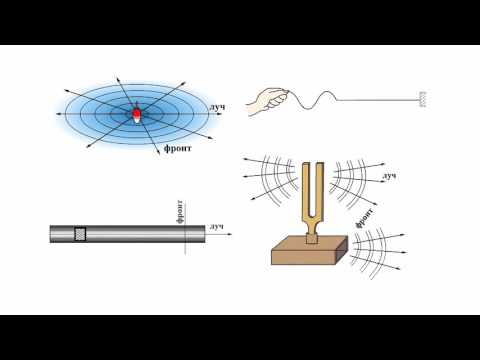
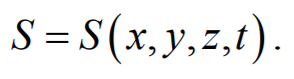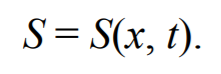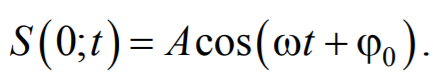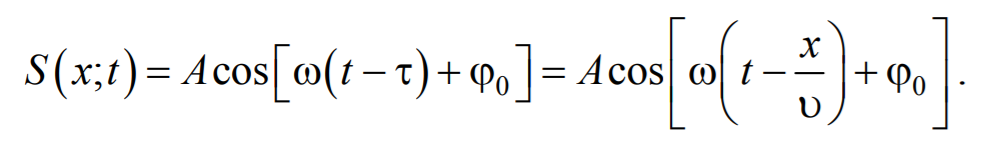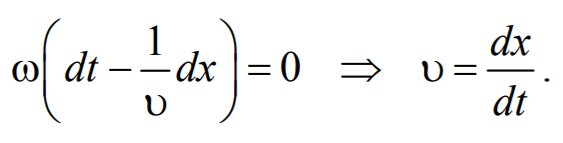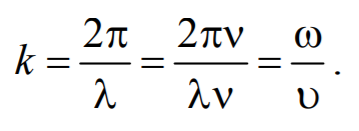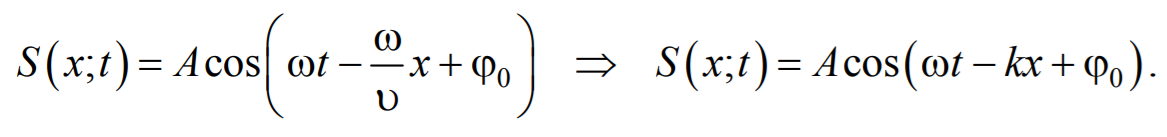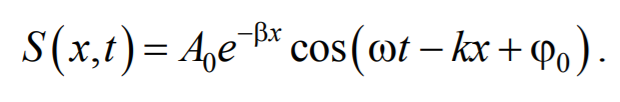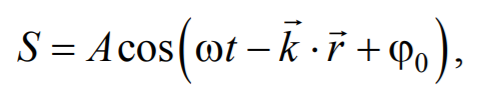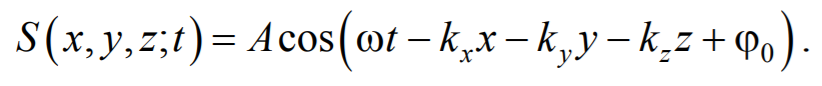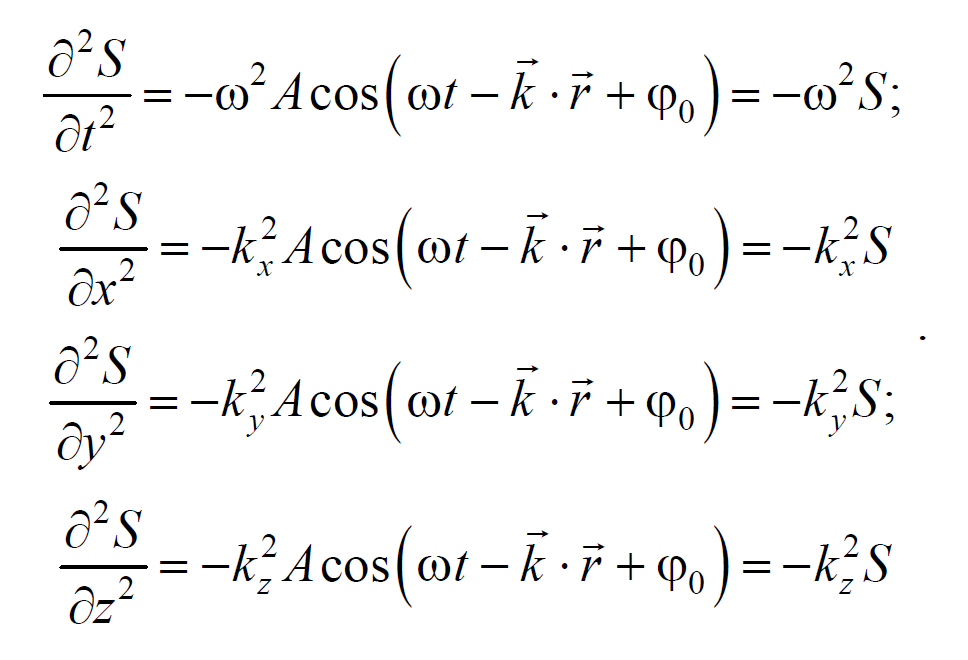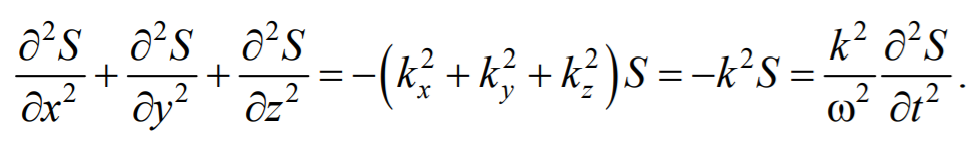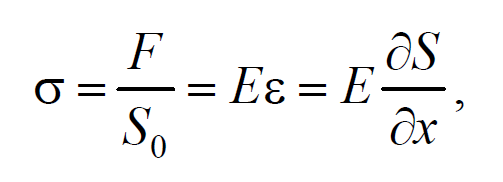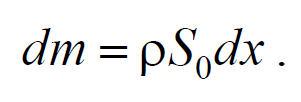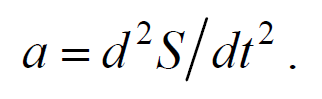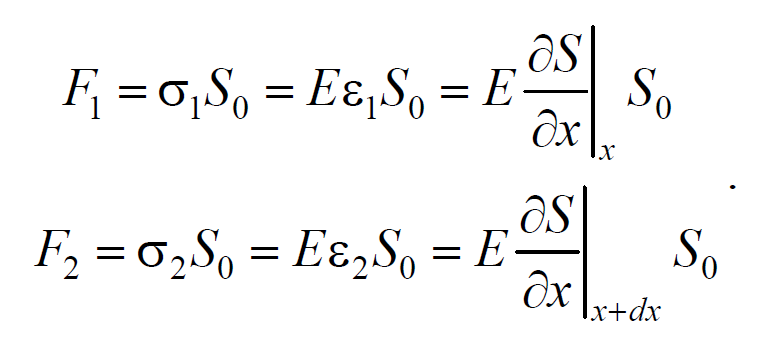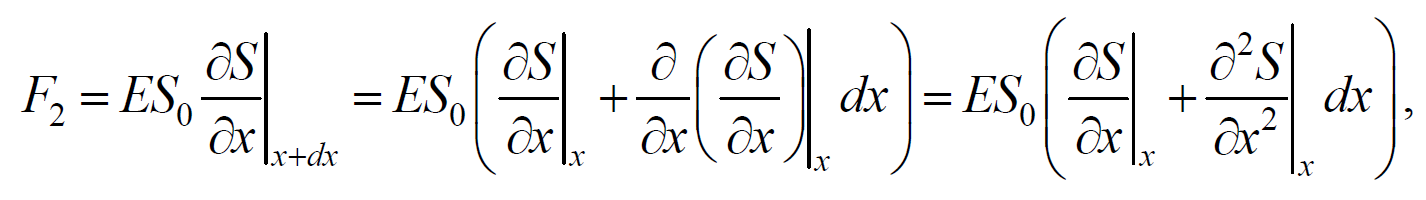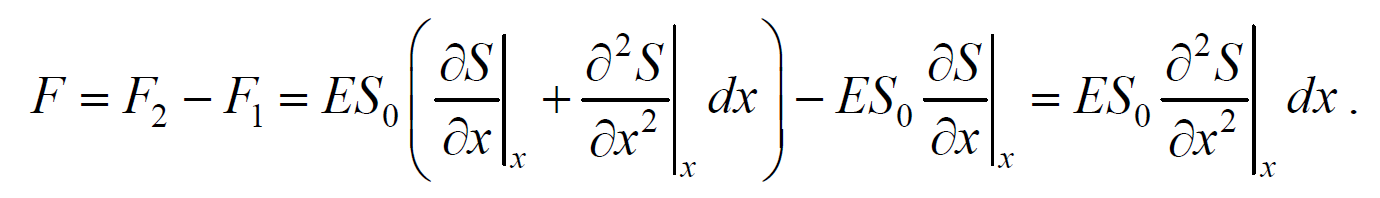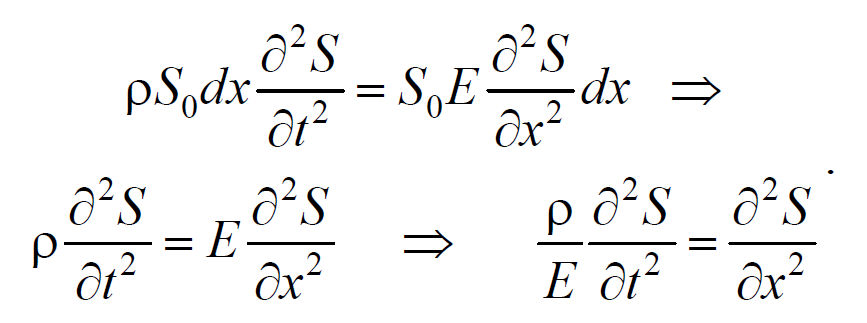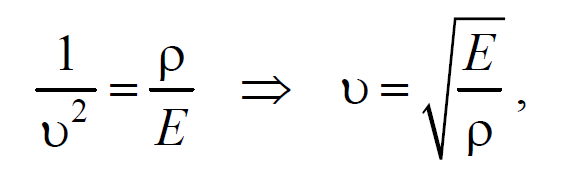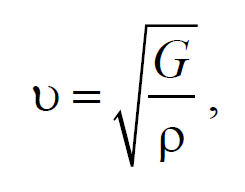Отвлечемся от внутреннего строения вещества для того, чтобы исследовать законы распространения механических волн. Вещество будем рассматривать как сплошную среду, непрерывно изменяющуюся в пространстве.
Частицей, изучая колебания, будем называть малый элемент объема среды, размеры которого много больше, чем расстояния между молекулами, при этом частицу среды принимаем за материальную точку.
Рассматривая механические волны, будем считать вещества, в которых они распространяются, упругими, внутренние силы, возникающие в них при малых деформациях, пропорциональными величине деформации.
При возбуждении колебания, в каком- либо месте упругой среды, в результате взаимодействия частиц среды, оно распространяется в веществе от точки к точке с некоторой конечной скоростью. Процесс распространения колебаний называют волной. Важным свойством волнового процесса является то, что в нем не происходит переноса массы, каждая частица выполняет колебания около положения равновесия. В волне от частицы к частице передается состояние колебательного движения и энергия колебаний. Волна переносит энергию.
В зависимости от направления колебаний частицы вещества по отношению к направлению распространения волны, волны делят на продольные и поперечные.
- Продольные волны
- Поперечные волны
- Уравнение продольной и поперечной волны
- Примеры задач с решением
- Волновое уравнение
- Эффект Доплера
- Лекция №9. Механические волны
- 6.1. Распространение колебаний в упругой среде
- 6.2. Уравнение плоской волны
- 6.3. Волновое уравнение
- 6.4. Скорость распространения волн в различных средах
- 💡 Видео
Видео:Механические модели волн. 1.Скачать

Продольные волны
Если частицы совершают колебания в направлении распространения волны, то такую волну называют продольной.
Продольные волны распространяются в веществе, в котором возникают силы упругости, при деформации растяжения и сжатия в веществе в любом агрегатном состоянии.
Так, например, волны звука, распространяющиеся в воздухе, относят к продольным волнам. Продольные волны, имеющие частоты от 17 до 20
000 Гц называют звуковыми. Скорость распространения акустических волн зависит от свойств среды и ее температуры.
При распространении продольной волны в среде возникают чередования сгущений и разрежений частиц, перемещающихся в направлении распространения волны со скоростью $v$. Все время существования волны, элементы среды выполняют колебания у своих положений равновесия, при этом разные частицы совершают колебания со сдвигом по фазе. В твердых телах скорость распространения продольных волн больше, чем скорость поперечных волн.
Скорость распространения продольных упругих волн в однородных в газах или жидкостях равна:
где $K$ — модуль объемной упругости вещества; $rho =const$ — плотность среды. В газах формула (1) справедлива, если избыточное давление много меньше, чем равновесное давление невозмущенного газа.
Скорость распространения продольных волн в тонком стержне, вызванных его продольным растяжением и сжатием равна:
где $E$ — модуль Юнга вещества стержня.
Видео:Билет №34 "Электромагнитные волны"Скачать

Поперечные волны
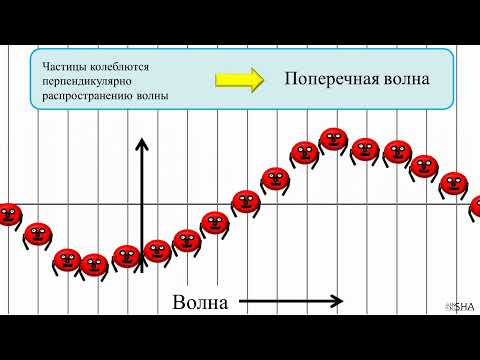
Поперечной волной называют такую волну, в которой колебания частиц среды происходят в направлениях перпендикулярных к направлению распространения волны.
Механические волны могут быть поперечными только в среде, в которой возможны деформации сдвига (среда обладает упругостью формы). Следовательно, в жидкостях и газах механических поперечных волн не наблюдают. Поперечные механические волны возникают в твердых телах. Примером таких волн являются волны, которые распространяются в натянутых струнах.
Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде можно вычислить как:
где $G$ — модуль сдвига среды; $rho $ — плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
Приведенная здесь скорость распространения упругих волн называется фазовой скоростью.
Видео:🌊 Продольные и поперечные волны ⚛ ФизикаСкачать
Уравнение продольной и поперечной волны
Основной задачей при изучении волн является установление закона изменения во времени и пространстве физических величин, которые однозначно характеризуют движение волны. При рассмотрении упругих волн такой величиной служит, например, смещение ($s$) частиц среды от их положений равновесия. Функция $s$ в зависимости от координат пространства и времени называется уравнением волны.
Самым простым видом волн являются гармонические волны. В таких волнах параметры $s$ для всех частиц среды, которые охвачены волной, совершают гармонические колебания с одинаковыми частотами. Для реализации данного волнового процесса необходимо, чтобы источник гармонических волн совершал незатухающие гармонические колебания.
Уравнение одномерной волны записывают как:
$k$ — волновое число; $lambda $ — длина волны; $A$ — амплитуда волны в точке (если среда не поглощает энергию, то амплитуда колебаний совпадает с амплитудой колебаний источника волн); $left[omega t-kx+varphi right]$ — фазой волны; $omega $- циклическая частота колебаний; $varphi $ — начальная фаза.
Видео:10й класс; Физика; "Уравнение плоской волны"Скачать

Примеры задач с решением
Задание: Поперечная волна распространяется по натянутой струне со скоростью $v=2frac$, период колебаний точек струны равен T= 1 с, амплитуда колебаний составляет 0,05 м. Какими будут смещение и скорость малого элемента струны, который находится на расстоянии $x_1=1 $м от источника колебаний в момент времени $t_1$=2 c?
Решение: Основой для решения задачи служит уравнение одномерной волны:
где $s$ — смещение точки струны, совершающей колебания; $x$ — расстояние от источника волны до рассматриваемой точки; $k=frac$ — волновое число; $v$ — скорость распространения волны.
Циклическую частоту $omega $ найдем (при T=1 c) как:
Тогда волновое число при $v=2frac$ равно:
Уравнение для нашей волны в учетом данных задачи приобретет вид:
Смещение точки струны, находящейся на расстоянии $x_1=1 $м от источника колебаний в момент времени $t_1$=2 c будет равно:
Скорость рассматриваемой точки струны найдем как:
Ответ: $s_1=-0,05$ м; $frac
Задание: Плоская одномерная волна распространяется в упругой среде. Изобразите на графике направление скорости частиц среды в точках $s=0, $при t=0 для продольной и поперечной волн.
Решение: Уравнением одномерной плоской волны служит выражение:
При $t=0 c$ из выражения (2.1) получаем:
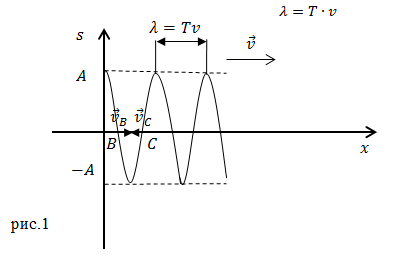
В продольной волне частицы смещаются вдоль направления скорости движения волны (рис.1).
В продольной волне частицы совершают колебания поперек направления скорости движения волны рис.2.
Видео:Волновое движение. Механические волны. 9 класс.Скачать

Волновое уравнение
Уравнение любой волны есть решение некоторого дифференциального уравнения, называемого волновым.
Найдем общий вид волнового уравнения. Для этого продифференцируем дважды уравнение плоской волны ?, = Л cos(co/ — кг) по времени t и всем координатам. Учтем при этом, что и = со /к. Окончательно получим для волнового уравнения:
Всякая функция, удовлетворяющая уравнению (2.4.14), описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту /v 2 при производной по времени, есть фазовая скорость волны.
Используя оператор Лапласа уравнение
(2.4.14) можно записать в виде
Видео:Урок 370. Механические волны. Математическое описание бегущей волныСкачать

Эффект Доплера
Известно, что при приближении к неподвижному наблюдателю быстро движущегося электропоезда его звуковой сигнал кажется более высоким, а при удалении от наблюдателя — более низким, чем сигнал того же электропоезда, но неподвижного.
Эффект Доплера, названный в честь австрийского физика К. Доплера (1803—1853), представляет собой изменение частоты волн, регистрируемой приемником, которое происходит вследствие движения источника этих волн и приемника.
Источник, двигаясь к приемнику, как бы сжимает пружину — волну (рис. 2.4.7).
Рис. 2.4.7. Эффект Доплера — изменение частоты волны, регистрируемой приемником от движущегося источника
Данный эффект наблюдается при распространении звуковых волн (iакустический эффект) и электромагнитных волн (оптический эффект).
Акустический эффект Доплера
Рассмотрим несколько случаев проявления акустического эффекта Доплера.
1. Пусть приемник звуковых волн П в газообразной (или жидкой) среде неподвижен относительно нее, а источник И удаляется от приемника со скоростью ии вдоль соединяющей их прямой (рис. 2.4.8, а).
Рис. 2.4.8. Несколько случаев проявления эффекта Доплера
Источник смещается в среде за время, равное периоду Т0 его колебаний, на расстояние— частота колебаний источника. Поэтому при движений 
где v — фазовая скорость волны в среде.
Частота волны, регистрируемая приемником,
Если вектор vH скорости источника направлен под произвольным углом 0, к радиусу-вектору R, соединяющему неподвижный приемник с источником (рис. 2.4.8, б), то
2. Если источник неподвижен, а приемник приближается к нему со
скоростью ип вдольсоединяющей их прямой (рис. 2.4.8, в), то длина
волны в среде 
относительно приемника равна v + va, так что частота волны, регистрируемая приемником,
В том случае, когда скорость vn направлена под произвольным углом 02 к радиусу-вектору R, соединяющему движущийся приемник с неподвижным источником (рис. 2.4.8, г), имеем
3. В самом общем случае, когда и приемник, и источник звуковых волн движутся относительно среды с произвольными скоростями (рис. 2.4.8, д), частота волны, регистрируемая приемником,
Оптический эффект Доплера
При движении источника и приемника электромагнитных волн относительно друг друга также наблюдается эффект Доплера, т.е. изменение частоты волны, регистрируемой приемником. В отличие от рассмотренного нами эффекта Доплера в акустике, закономерности этого явления для электромагнитных волн можно установить только на основе специальной теории относительности.
Соотношение, описывающее эффект Доплера для электромагнитных волн в вакууме, с учетом преобразований Лоренца имеет вид
При небольших скоростях движения источника волн относительно приемника релятивистская формула эффекта Доплера совпадает с классической формулой.
Если источник движется относительно приемника вдоль соединяющей их прямой, то наблюдается продольный эффект Доплера.
В случае сближения источника и приемника (0 = тс)
а в случае их взаимного удаления (0 = 0)
Кроме того, из релятивистской теории эффекта Доплера следует существование поперечного эффекта Доплера, наблюдаемого при 0 = л/2 и 0 = Зл/2, т.е. в тех случаях, когда источник движется перпендикулярно линии наблюдения (например, источник движется по окружности, в центре которой находится приемник):
Поперечный эффект Доплера необъясним в классической физике, это чисто релятивистский эффект.
Как видно из формулы (2.4.19), поперечный эффект пропорционален отношению и 2 /с 2 , следовательно, он значительно слабее продольного, который пропорционален и/с [см. формулу (2.4.18)].
Эффект Доплера нашел широкое применение в науке и технике. Особенно большую роль это явление играет в астрофизике. На основании доплеровского смещения линий поглощения в спектрах звезд и туманностей можно определять лучевые скорости t/cos0 этих объектов по отношению к Земле: при v«с по формуле
В 1929 г. американский астроном Э. Хаббл (1889—1953) обнаружил явление, получившее название космологического красного смещения и состоящее в том, что линии в спектрах излучения внегалактических объектов смещены в сторону меньших частот (больших длин волн). Оказалось, что для каждого объекта относительное смещение частоты z = (v0 — v)/v0 (где v0 — частота линии в спектре неподвижного источника, v — наблюдаемая частота) совершенно одинаково по всем частотам.
Космологическое красное смещение есть не что иное, как эффект Доплера. Оно свидетельствует о том, что Метагалактика расширяется так, что внегалактические объекты удаляются от нашей Галактики. Под Метагалактикой понимают совокупность всех звездных систем. В современные телескопы можно наблюдать часть Метагалактики, оптический радиус которой R = 1,12 -10 23 км. Явление расширения Метагалактики было теоретически предсказано еще в 1922 г. советским ученым А.А. Фридманом (1888—1925) на основе развития общей теории относительности.
Хаббл установил закон, согласно которому относительное красное смещение z галактик растет пропорционально расстоянию г до них (рис. 2.4.9).
Рис. 2.4.9. Зависимость скорости удаления галактик от расстояния до них Закон Хаббла можно записать в виде
где Н — постоянная Хаббла. По современным оценкам, значение Н = 73,2 км/(с- Мпк), 1 пк (парсек) — расстояние, которое свет проходит в вакууме за 3,27 года (1 пк
Чем дальше находится галактика, тем больше ее красное смещение, и поэтому больше скорость ее удаления.
В 1990 г. на борту шаттла «Дискавери» был выведен на орбиту космический телескоп имени Хаббла (рис. 2.4.10).
Рис. 2.4.10. Космический телескоп «Хаббл»
Астрономы давно мечтали о телескопе, который работал бы в видимом диапазоне, но находился за пределами земной атмосферы, сильно мешающей наблюдениям. «Хаббл» не только не обманул возлагавшихся на него надежд, но даже практически превзошел все ожидания. Он фантастически расширил поле зрения человечества, заглянув в немыслимые глубины Вселенной. За время своей работы космический телескоп передал на землю 700 тыс. великолепных фотографий (рис. 2.4.11). Он, в частности, помог астрономам определить точный возраст нашей Вселенной (13,7 млрд лет) и подтвердить существование в ней странной, но оказывающей огромное влияние формы энергии — темной энергии; доказал существование сверхмассивных черных дыр; удивительно четко заснял падение кометы на Юпитер; показал, что процесс формирования планетных систем является широко распространенным в нашей Галактике; обнаружил небольшие протогалактики, зарегистрировав излучение, испущенное ими, когда возраст Вселенной составлял менее 1 млрд лет.
Рис. 2.4.11. Фотография Галактики
На эффекте Доплера основаны радиолокационные лазерные методы измерения скоростей различных объектов на Земле (например, автомобиля, самолета и др.). Лазерная анемометрия (учение об измерении ветра) является незаменимым методом изучения потока жидкости или газа. Хаотическое тепловое движение атомов светящегося тела также вызывает уширение линий в его спектре, которое возрастает с увеличением скорости теплового движения, т.е. с повышением температуры газа. Это явление можно использовать для определения температуры раскаленных газов.
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Лекция №9. Механические волны
6.1. Распространение колебаний в упругой среде
Механические колебания, распространяющиеся в упругой среде (твердой, жидкой или газообразной), называются механическими или упругими волнами .
Процесс распространения колебаний в сплошной среде называется волновым процессом или волной. Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение. Они лишь совершают колебания около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества .
В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны.
Упругая волна называется продольной , если колебания частиц среды происходят в направлении распространения волны. Продольные волны связаны с объемной деформацией растяжения − сжатия среды, поэтому они могут распространяться как в твердых телах, так и в жидкостях и газообразных средах.
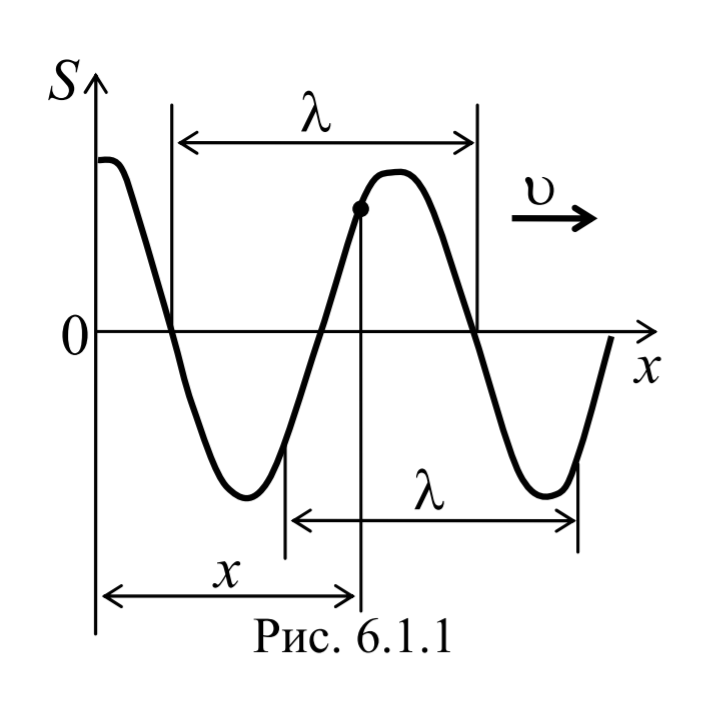
На рис. 6.1.1 представлена гармоническая поперечная волна, распространяющаяся вдоль оси 0х . График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны . Длина волны также равна тому расстоянию, на которое распространяется определенная фаза колебания за период колебаний
Колеблются не только частицы, расположенные вдоль оси 0х , а совокупность частиц, заключенных в некотором объеме. Геометрическое место точек, до которых доходят колебания к моменту времени t , называется фронтом волны . Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью . Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, а в сферической − множество концентрических сфер.
6.2. Уравнение плоской волны
Уравнением плоской волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат x , y , z и времени t
Эта функция должна быть периодической как относительно времени t , так и относительно координат x , y , z . Периодичность по времени вытекает из того, что смещение S описывает колебания частицы с координатами x , y , z , а периодичность по координатам следует из того, что точки, отстоящие друг от друга на расстоянии, равном длине волны, колеблются одинаковым образом.
Предположим, что колебания носят гармонический характер, а ось 0х совпадает с направлением распространения волны. Тогда волновые поверхности будут перпендикулярны оси 0х и, поскольку все точки волновой поверхности колеблются одинаково, смещение S будет зависеть только от координаты х и времени t
Рассмотрим некоторую частицу среды, находящуюся от источника колебаний О на расстоянии х . Пусть колебания точек, лежащих в плоскости х = 0 имеют вид
Найдем вид колебания точек в плоскости, соответствующей произвольному значению х . Для того, чтобы пройти путь от плоскости х = 0 до плоскости х , волне требуется время τ = x/υ . Следовательно, колебания частиц, лежащих в плоскости х , будут отставать по времени на τ от колебаний частиц в плоскости х = 0 и описываться уравнением
где А − амплитуда волны; ϕ0 − начальная фаза волны (определяется выбором начал отсчета х и t ).
Зафиксируем какое-либо значение фазы ω(t-x/υ)+ϕ0=const. Это выражение определяет связь между временем t и тем местом х , в котором фаза имеет фиксированное значение. Продифференцировав данное выражение, получим
Таким образом, скорость распространения волны есть скорость перемещения фазы, и называется фазовой скоростью .
При υ > 0 волна распространяется в сторону возрастания х . Волна, распространяющаяся в противоположном направлении, описывается уравнением
Придадим уравнению плоской волны симметричный относительно х и t вид. Для этого введем величину $$k = $$ , которая называется волновым числом , которое можно представить в виде
Тогда уравнение плоской волны будет иметь вид
Мы предполагали, что амплитуда колебаний не зависит от х . Для плоской волны это наблюдается в том случае, когда энергия волны не поглощается средой. При распространении в поглощающей энергию среде интенсивность волны с удалением от источника колебаний постепенно уменьшается, т. е. наблюдается затухание волны. В однородной среде такое затухание происходит по экспоненциальному закону A=A0e −βx . Тогда уравнение плоской волны для поглощающей среды имеет вид
6.3. Волновое уравнение
Уравнение плоской волны, распространяющейся в произвольном направлении, будет иметь вид
где r − радиус-вектор, точки волны; r =k× n − волновой вектор ; n − единичный вектор нормали к волновой поверхности
Волновой вектор − это вектор, равный по модулю волновому числу k и имеющий направление нормали к волновой поверхности называется.
Перейдем от радиус-вектора точки к ее координатам x , y , z 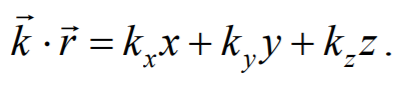
Установим вид волнового уравнения. Для этого найдем вторые частные производные по координатам и времени выражение (6.3.3)
Сложив производные по координатам, и с учетом производной по времени, получим
6.4. Скорость распространения волн в различных средах
Для определения скорости упругих волн в упругой среде рассмотрим продольную плоскую волну, распространяющуюся в направлении оси 0х . Выделим в среде цилиндрический объем с площадью основания S0 и высотой dx . Смещения S частиц с разными х в каждый момент времени оказываются различными. Если основание цилиндра с координатой х имеет в некоторый момент времени смещение S , то смещение основания с координатой x+dx будет S+dS . Тогда, рассматриваемый объем деформируется и получает удлинение dS или относительную деформацию ε=∂S/∂x (деформации растяжения). Наличие деформации свидетельствует о существовании нормального напряжения σ , которое при малых деформациях пропорционального величине деформации. По закону Гука для деформации растяжения − сжатия
где Е − модуль Юнга среды.
Из зависимости смещения от координаты x видно, что относительная деформация ∂S/∂x , а также, и напряжение σ в фиксированный момент времени зависят от х . В соответствии с этим, продольная волна состоит из чередующихся разрежений и сжатий среды.
Теперь для цилиндрического объема запишем уравнение движения. Масса этого объема
где ρ − плотность недеформированной среды.
Ввиду малости dx можно считать ускорение всех точек цилиндра одинаковым и равным
Тогда этот участок объема будет растянут под влиянием сил F1 и F2 , приложенных к основаниям цилиндра в данный момент времени. Силы, действующие на левое и правое основание цилиндра равны, соответственно
После разложения силы F2 в ряд, получим
и результирующая F1 , F2 сил, действующая на элемент объема равна
Используя основное уравнение динамики поступательного движения (2.1.2) и, подставив значения массы, ускорения и силы, получим
Из сравнения этого уравнения с волновым уравнением для плоской волны (6.3.6) $$=$$ , получим
где Е − модуль Юнга.
Полученное уравнение определяет фазовую скорость продольных упругих волн.
Если проделать аналогичные преобразования для поперечных упругих волн, то фазовая скорость поперечных упругих волн будет иметь следующий вид
💡 Видео
Колебания и волны. Лекция 10. Уравнения сферической и плоской волныСкачать

4.2 Решение волновых уравнений Гельмгольца в виде плоских бегущих волнСкачать

Физика 11 класс (Урок№2 - Механические волны.)Скачать

Урок 95 (осн). Механические волны. ЗвукСкачать

Якута А. А. - Механика - Волновое уравнение. Механические волны. Скорость распространения волнСкачать

74. Упругие волныСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Механические модели волн. 2.Скачать

Лекция 2 ВолныСкачать

Получение уравнения плоской бегущей волны.Скачать

Упругие механические волны. 1 часть. 11 класс.Скачать

5.6 Механические волны. Виды волнСкачать