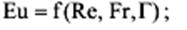Дифференциальное уравнение неразрывности потока для неустановившегося движения сжимаемой жидкости

Видео:Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Для круглого трубопровода и несжимаемой жидкости объемный расход

рассчитывается по уравнению:

Сплошной (неразрывный) поток жидкости – поток, в котором отсутствуют пустоты, движение происходит с непрерывным распространением массы; масса жидкости, проходящая через любое сечение, согласно закону сохранения массы, есть величина постоянная.

Уравнение неразрывности (сплошности) потока в дифференциальной форме:

– дифференциальное уравнение неразрывности потока для неустановившегося движения сжимаемой жидкости;

– дифференциальное уравнение неразрывности потока для установившегося движения сжимаемой жидкости;

=

– дифференциальное уравнение неразрывности потока для установившегося движения несжимаемой жидкости,

– изменение скоростей вдоль осей координат x,y,z.

Уравнение неразрывности потока в интегральной форме – уравнение постоянства расхода:

Скорости капельной жидкости в различных поперечных сечениях трубопровода обратно пропорциональны площадям этих сечений:

.

Гидравлический радиус– отношение площади S сечения потока к смоченному периметру П, характеризует каналы некруглого сечения:

Эквивалентный диаметр – геометрическая характеристика канала некруглого сечения, равен отношению учетверенной площади живого сечения, через которое протекает жидкость, к смоченному периметру:

Движение жидкости – перемещение жидкости по трубопроводам, аппаратам, каналам и т.д. Различают установившееся и неустановившееся, свободное и вынужденное, напорное и безнапорное движения. При установившемся движении поля давлений и скоростей не изменяются во времени, а при неустановившемся – изменяются. Свободное движение возникает за счет разности плотностей в различных точках объема жидкости. Вынужденное движение создается внешними силами, создаваемыми насосами, мешалками, центрифугами и др. При напорном течении жидкость заполняет все сечение трубопровода, при безнапорном – только часть сечения заполнена жидкостью, имеется свободная поверхность. Различают ламинарный и турбулентный режимы движения жидкостей.

Критерий Рейнольдса — единый безразмерный комплекс, по численному значению которого можно судить о режимах течения жидкости, является мерой соотношения между силами инерции и силами вязкости. Переход от ламинарного режима к турбулентному осуществляется тем легче, чем больше массовая скорость жидкости ρw, чем больше диаметр трубы и чем меньше вязкость жидкости:

Ламинарный режим движения– все частицы жидкости перемещаются равномерно по параллельным траекториям. Наблюдается при значениях критерия Рейнольдса меньше критического Re_кр (Re Re_кр =2320) в прямых и гладких трубах постоянного сечения. В интервале значений 2320

Дифференциальные уравнения движения идеальной жидкости Эйлера– частный случай закона сохранения энергии для потока идеальной жидкости:

– проекции ускорения на оси координат.

В движущейся жидкости изменение давления происходит благодаря действию объемных сил, силы тяжести и силы инерции. Примером может служить явление гидравлического удара – при внезапном закрытии крана в трубе резко возрастает давление, происходит торможение жидкости, и энергия движения переходит в энергию давления, что может привести к разрыву трубопровода. Интегральным решением дифференциальных уравнений Эйлера является уравнение Д.Бернулли – для любого сечения потока при установившемся движении идеальной жидкости сумма геометрического z, пьезометрического и скоростного w 2 /g2 напоров (высот) есть величина постоянная, равная суммарному (полному) гидродинамическому напору; данное уравнение выражает закон сохранения энергии – для движущейся среды любого сечения потока при установившемся движении идеальной жидкости сумма удельной (отнесенной к 1Н жидкости) потенциальной

энергий есть величина постоянная:

или для двух поперечных сечений потока

Дифференциальные уравнения движения реальной жидкости Навье – Стокса – выражают связь между массовыми, поверхностными, инерционными и вязкостными силами в потоке, характеризуют закон сохранения энергии при движении вязкой жидкости:

где ∇ 2 w_x, ∇ 2 w_y ∇ 2 w_z – операторы Лапласа, представляют собой суммы вторых производных по осям координат. Согласно второй теореме подобия решение уравнений Навье – Стокса можно представить в виде обобщенного критериального уравнения гидродинамики:

для установившегося движения реальной жидкости

где Eu – критерий Эйлера, определяемый критерий; Re, Fr, Ho — критерии Рейнольдса, Фруда, гомохронности, являются определяющими критериями; Г – симплекс геометрического подобия.

В виде степенной зависимости критериальное уравнение принимает вид:

где A, m, n, p, q – постоянные, определяемые опытным путем для группы подобных явлений.

Основные критерии гидродинамического подобия представлены в табл. 2.

1. Какие процессы называются тепловыми?

2. Дайте определение движущей силы тепловых процессов.

3. Сформулируйте определения температурного поля, изотермической поверхности и температурного градиента.

4. Какими способами осуществляется перенос тепла в теплообменных процессах?

5. Запишите закон теплопроводности Фурье. Сформулируйте физический смысл и укажите размерность коэффициента теплопроводности.

6. В каких единицах измеряется коэффициент температуропроводности?

7. Запишите уравнения теплопроводности плоской и цилиндрической стенок.

8. Сформулируйте законы теплового излучения.

9. Что называется процессом теплоотдачи? От каких факторов зависит коэффициент теплоотдачи, в каких единицах измеряется?

10. Назовите основные критерии теплового подобия и сформулируйте их физический смысл.

11. Каким образом определяется коэффициент теплоотдачи в случае пленочной конденсации?

12. Что такое теплопередача? Укажите физический смысл, размерность коэффициента теплопередачи.

13. Каким образом определяется средняя движущая сила процесса теплопередачи при различных взаимных направлениях теплоносителей?

14. Что является целью расчета теплообменного аппарата?

15. Дайте классификацию теплообменных аппаратов.

16. Назовите основные греющие агенты в зависимости от температуры нагреваемой среды.

17. Каким образом осуществляется умеренное и глубокое охлаждение?

18. Какие типы конденсаторов различают по способу охлаждения?

19. Что такое выпаривание?

20. Дайте классификацию выпарных установок.

21. Перечислите основные типы выпарных аппаратов.

22. Запишите тепловой и материальный балансы однокорпусного выпаривания.

23. Сформулируйте понятия первичного и вторичного паров.

24. Что такое температурные потери и полезная разность температур?

25. Каким образом рассчитывается температура кипения раствора?

Видео:Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Уравнение неразрывности (сплошности) потока

Это уравнение представляет собой зависимость между скоростями в потоке жидкости, для которого соблюдается условие сплошности, или неразрывности течения, т.е. в жидкости не образуется незаполненных пустот.

Уравнение выражает фундаментальный закон сохранения массы (расхода).

Дифференциальное уравнение неразрывности для неустановившегося течения имеет вид

В установившемся потоке плотность не меняется во времени |^ = oj, поэтому уравнение неразрывности выглядит так:

Для капельных жидкостей, которые практически несжимаемы, а также для газов в условиях изотермического потока при скоростях, меньших скорости звука, р — const, следовательно, уравнение неразрывности примет вид

Для трубопровода постоянного сечения в результате интегрирования дифференциального уравнения неразрывности для установившегося однонаправленного движения жидкости (в направлении оси х) получается зависимость

Если же площадь сечения трубопровода переменна, то интегрирование по площади приводит к зависимости

Для трех сечений трубопровода одного и того же потока жидкости (рис. 2.6): или для массового расхода жидкости в трубопроводе переменного сечения:

Согласно уравнению постоянства расхода, при установившемся течении жидкости, полностью заполняющей трубопровод, через каждое его поперечное сечение проходит в единицу времени одно и то же количество жидкости

или для объемного расхода жидкости в трубопроводе переменного сечения

Из уравнения (2.5) следует, что скорости капельной жидкости в различных поперечных сечениях трубопровода обратно пропорциональны площадям этих сечений.

В соответствии с уравнением (2.4), массовый расход жидкости через начальное сечение трубопровода равен ее расходу через конечное сечение трубопровода (рис. 2.6). Таким образом, уравнение неразрывности является частным случаем закона сохранения массы и выражает материальный баланс потока.

Рис. 2.6. К выводу уравнения (2.4)

Видео:Вывод уравнений движения идеальной жидкости - Лекция 2Скачать

Режимы движения жидкостей

Характер движения жидкости зависит от скорости ее течения. Этот вопрос был решен в 1883 г. О. Рейнольдсом, который поставил простой убедительный опыт. Установка О. Рейнольдса показана на рис. 2.7. Характер движения жидкости устанавливается по степени размытости струйки подкрашенной жидкости, истекающей по трубке 2 из сосуда 1. В зависимости от высоты уровня жидкости в сосуде 1 устанавливалась та или иная скорость течения.

При малых скоростях течения струя окрашенной жидкости 3 не размывалась, что указывало на послойный характер движения жидкости. Такие течения были названы ламинарными.

Рис. 2.7. Опыт Рейнольдса:

а — ламинарное движение; б — турбулентное движение

При некоторой критической скорости струйка размывалась по всему сечению, что свидетельствовало о вихревом характере перемешивания жидкости по всему сечению трубы 4. Такой режим течения был назван турбулентным. Рейнольдс показал, что переход от одного режима течения к другому соответствует определенному значению безразмерной величины:

где w — средняя скорость; d — диаметр канала; v — кинематический коэффициент вязкости жидкости.

Видео:Закон БернуллиСкачать

Уравнение неразрывности и уравнение Бернулли.

Уравнение неразрывности потока и уравнения Бернулли являются основными уравнениями гидродинамики. При изучении потоков жидкости вводится ряд понятий, характеризующий потоки с гидравлической и геометрической точек зрения.

Такими понятиями являются: площадь живого сечения потока(или живое сечение потока), расход и средняя скорость.

Площадью живого сечения потока, называют площадь сечения потока, приведенную нормально к направлению линии тока, т.е. перпендикулярно движению струйки жидкости. Живое сечение может быть ограничено твердыми стенками полностью или частично. Если стенки ограничивают поток полностью, то движение жидкости называют напорным; Если же ограничение частичное, то движение называется безнапорным.

Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше него. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному.

Содержание статьи

Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.

Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным. Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью. Эту воображаемую фиктивную скорость называют средней скоростью потока υ_ср .

Таким образом уравнение расхода для потока будет

υ_ср – средняя скорость потока

F – площадь сечения потока.

Видео:Галилео. Эксперимент. Закон БернуллиСкачать

Уравнение неразрывности потока жидкости

Теперь вооружившись основными понятиями перейдем к определению уравнения неразрывности потока.

Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный

а через сечение 2-2 из него же вытекает объем, равный

Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.

Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.

Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки

Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что

т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.

Уравнение неразрывности струи жидкости. Уравнение Бернулли.

Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.

При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.

Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.

Если всё это записать в виде формулы, то

где W – приращение кинетической энергии = m * υ 2 / 2

ΣA – сумма работ действующих сил = P *ΔS

В этих выражениях
m – масса
υ – скорость материальной точки
P – равнодействующая всех сил, приложенных к точке,
ΔS – проекция перемещения точки на направление силы.

Теперь рассмотрим обе части этого выражения по порядку.

Приращение кинетической энергии ΔW

В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.

Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.

Вспоминая, что по условию неразрывности расход во всех сечениях элементарной струйки одинаков, а следовательно будет равен

масса в этом случае получается равной

Подставляя все это в выражение для кинетической энергии получаем цепочку

ΔW = m * υ 2 ₂ / 2 — m * υ 2 ₁ / 2 = ρ * q * ΔТ * υ 2 ₂ / 2 — ρ * q * ΔТ * υ 2 ₁ / 2

Работа сил действующих на систему ΣA

Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести A_Т равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.

Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z1 –Z2.

Где Z1 и Z2 – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.

Силы давления А_Д , действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.

Суммарно работа сил давления будет

Подставляя в начальное уравнение

Полученные выражения для ΔW и ΣA получаем

Разделим обе части этого уравнения на m = ρ*q*ΔТ и перегруппируем слагаемые

Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:

Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки. Различают такие энергии как:
Удельная энергия положения = qz
Удельная энергия давления = p/ ρ
Кинетическая удельная энергия = υ 2 / 2

В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Видео по теме уравнение неразрывности

Полученные в результате многочисленных экспериментов данные из уравнения Бернулли и уравнения неразрывности потока жидкости нашли широкое применение в повседневной жизни.

Уравнение Бернулли широко используется для нахождения скорости истечения жидкости через отверстия.

Уравнение неразрывности обладает широкой универсальностью и справедливо для любой сплошной среды. Принцип уравнения неразрывности используется для формирования сильной и дальнобойной струи воды при тушении пожаров.

📽️ Видео

Уравнение Бернулли для потока жидкостиСкачать

Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

14. Движение идеальной жидкостиСкачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Вывод уравнения неразрывности - Лекция 1Скачать

9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Дифференциальные уравнения. 11 класс.Скачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать

Дифференциальные уравнения не разрешенные относительно производной | poporyadku.schoolСкачать