Дифференциальное уравнение колебательного движения материальной точки дано в виде

Видео:Прямолинейные колебания материальной точкиСкачать

Дифференциальное уравнение колебательного движения материальной точки дано в виде

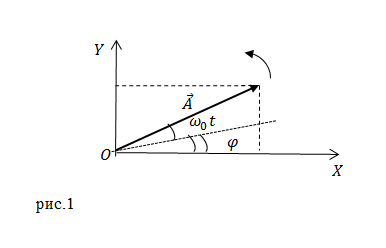
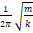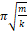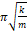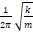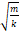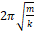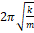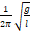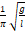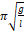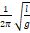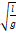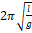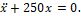Глава 13. Динамика точки.

13.6. Вынужденные колебания.

13.6.1. Дифференциальное уравнение колебательного движения матери­альной точки дано в виде х + 10x = 1,5 sin (5 t + 0,4). Определить мас­су точки, если максимальное значение вынуждающей силы F₀ = 60 Н. (Ответ 40)

13.6.2. На тело, которое подвешено к пружине, действует вертикальная вынуждающая сила F = 30 sin 20t. Определить коэффициент динамич­ности, если угловая частота собственных колебаний тела k = 25 рад/с. (Ответ 2,78)

13.6.3. Дифференциальное уравнение колебательного движения мате­риальной точки имеет вид у + 36у = 50sin(5t + 0,8). Определить коэффициент динамичности. (Ответ 3,27)

13.6.4. Статическое удлинение пружины под дей­ствием груза λ = 9,81 см. Определить коэффи­циент динамичности, если на груз действует вертикальная вынуждающая сила F = 15 sin 5t. (Ответ 1,33)

13.6.5. На тело массой m = 3кг, которое подвешено к пружине, дейст­вует вертикальная вынуждающая сила F = 10 sin 5t. Определить коэффициент жесткости пружины, если коэффициент динамичности η = 4. (Ответ 100)

13.6.6. На тело массой m = 50 кг. которое подвешено к пружине, дейст­вует вертикальная вынуждающая сила F = 200sin 10t. Определить коэффициент жесткости пружины в к H/м, если амплитуда вынужденных колебаний равна 0,04 м. (Ответ 10)

13.6.7. Дифференциальное уравнение движения вертикальных колебаний тела имеет вид х + 16х = 20 sin (6t + 0,7). Определить коэффициент жесткости пружины, к которой подвешено тело, если максимальное значение вынуждающей силы F_o = 80Н. (Ответ 64)

13.6.8. Дифференциальное уравнение колебательного движения матери­альной точки дано в виде 5х + 320х = 90 sin 7t. Определить угловую частоту собственных колебаний точки. (Ответ 8)

13.6.9. На тело, которое подвешено к пружине, действует вертикаль­ная вынуждающая сила F = 40 sin 10t. Определить угловую частоту собственных колебаний, если коэффициент динамичности η = 3. (Ответ 12,2)

13.6.10. На тело массой m = 0,5 кг, которое подвешено к пружине с коэф­фициентом жесткости с = 600 Н/м, действует вертикальная вынуж­дающая сила F = 25 sin pt. Определить, при какой угловой частоте р вынуждающей силы амплитуда вынужденных колебаний тела будет равна 0,05 м. (Ответ 14,1)

13.6.11. Дифференциальное уравнение колебаний материальной точки дано в виде х + 81х = 12 sin 5t. Определить амплитуду вынужденных колебаний. (Ответ 0,214)

13.6.12. На груз массой m = 0,1 кг, подвешенный на пружине с коэффициентом жесткости с = 0,5 Н/см, действует вынуждающая сила F = 0,3 sin t. Определить амплитуду вынужден­ных колебаний в мм. (Ответ 6,01)

13.6.13. Груз массой m = 18 кг, подвешенный к пружине с коэффициен­том жесткости с = 360 Н/м, совершает вертикальные колебания под действием вертикальной вынуждающей силы F = 36sin 3t. Опреде­лить амплитуду вынужденных колебаний. (Ответ 0,182)

13.6.14. Материальная точка массой m = 5 кг совершает колебания соглас­но уравнению у = 0,4 sin k t + 0,2 sin pt, где угловая частота собствен­ных колебаний k = 20 рад/с, а вынуждающей силы р = 10 рад/с. Опре­делить максимальное значение вынуждающей силы. (Ответ 300)

13.6.15. Дифференциальное уравнение движения вертикальных колебаний тела, подвешенного к пружине с коэффициентом жесткости с = 24 Н/м, имеет вид х + 8х = 1,2 sin(4t + 0,3). Определить максималь­ное значение вынуждающей силы. (Ответ 3.6)

13.6.16. Дифференциальное уравнение колебательного движения мате­риальной точки массой m = 4 кг дано в виде х + 7х = 0,5 sin(3t + 0,6). Определить максимальное значение вынуждающей силы. (Ответ 2)

13.6.17. Вынужденные колебания материальной точки массой m = 1 кг в случае резонанса за­даны графиком функции х = x(t). Определить максимальное значение действующей на точку вынуждающей силы F = F₀ sin pt. (Ответ 1,26)

13.6.18. Тело массой m = 0,5 кг подвешено к кон­цу пружины с коэффициентом жесткости с = 200 Н/м и совершает вынужденные колеба­ния под действием вынуждающей силы F = 15 sin pt Определить угловую частоту вынуждающей силы, при которой наступит ре­зонанс. (Ответ 20)

13.6.19. Определить амплитуду вынужденных колебаний материальной точки, если дифференциальное уравнение ее движения имеет вид х + 6х + 30х = 4 sin 2t. (Ответ 0,140)

13.6.20. Определить коэффициент динамичности, если дифференциальное уравнение вынужденных колебаний точки у + 8у + 250у = 6 sin 10t (Ответ 1,47)

13.6.21. На тело массой m = 10 кг, которое подвешено к пружине с коэф­фициентом жесткости с = 150 Н/м, действуют вертикальная вынуж­дающая сила F = 10 sin pt и сила сопротивления R = -8v. Определить максимальную амплитуду установившихся вынужденных колебаний, которую можно достичь, изменяя значения угловой частоты вынуж­дающей силы. (Ответ 0,324)

13.6.22. Тело массой m = 5 кг подвешено к пружине с коэффициентом жесткости с = 50 Н/м. Сила сопротивления движению R = -4v. Опре­делить, при какой угловой частоте вертикальной вынуждающей силы коэффициент динамичности будет максимальным. (Ответ 3,11)

13.6.23. Дифференциальное уравнение колебательного движения матери­альной точки массой m = 12 кг имеет вид у + 8у + 60у = 15 sin 3t. Сила сопротивления движению точки R = — ηy. Определить коэффи­циент η. (Ответ 96)

13.6.24. Дифференциальное уравнение колебательного движения материальной точки массой m = 3 кг имеет вид х + 4х + 30х = 15 sin 8t. Определить максимальное значение вынуждающей силы. (Ответ 45)

13.6.25. Тело массой m = 5 кг подвешено к пружине. Определить коэффи­циент жесткости пружины, если дифференциальное уравнение пря­молинейного поступательного движения тела имеет вид x + 6x + 40x = 5 sin 15t. (Ответ 200)

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Колебательное движение

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Определение и основные понятия колебательного движения

Колебательное движение (колебание) — это любое движение или изменение состояния, которое повторяется во времени, соответственно повторяются значения физических величин, которые характеризуют данное движение или состояние.

Различные физические явления представляют собой колебания: звуковые колебания, электромагнитные, механические и т.д. У всех этих явлений существует общее в законах и математических методах, при помощи которых они описываются.

Колебательное движение называется периодическим, если переменные параметры этих колебаний повторяются через равные промежутки времени.

Колебания называются свободными, если они происходят в системе, на которую не действуют внешние силы (или действие их взаимно скомпенсировано).

Такая система один раз выводится из состояния равновесия. Если колебательная система консервативная, то рассеяния энергии при колебаниях нет. В таком случае свободные колебания являются незатухающими. Свободные незатухающие колебания, которые происходят под воздействием упругих сил, являются гармоническими.

Периодом незатухающих колебаний называют минимальный промежуток времени ($T$) по истечении которого происходит повторение значений всех физических параметров, которые характеризуют колебание.

Частотой колебаний ($nu $) называют величину обратную периоду колебаний, это количество полных колебаний, которое совершает колебательная система:

Видео:Свободные колебания материальной точки 1Скачать

Гармонические колебания

Самым простым типом колебаний считают гармонические колебания.

Колебания называют гармоническими, если изменения физической величины описывается при помощи закона синуса или косинуса.

Пусть происходят гармонические колебания никоторого параметра $s$, тогда они описываются как:

где $A=s_$ — амплитуда колебаний (постоянна во времени); $_0$ — циклическая (круговая) частота колебаний (с течением времени не изменяется); $varphi $ — начальная фаза колебаний (фаза при $t=0$); $(_0t+varphi )$ — фаза колебаний. Величина $s$ изменяется $-Ale sle $+A.

Те же самые колебания можно описать как:

За время равное периоду колебаний фаза изменяется на величину равную $2pi $, поэтому:

Циклическая частота $_0$ равна числу полных колебаний, которые совершаются колебательной системой за $2pi $c:

Видео:Дифференциальные уравнения движения материальной точкиСкачать

Дифференциальное уравнение колебательного движения

Линейное дифференциальное уравнение гармонических колебаний представляет собой выражение:

Решениями уравнения (6) является выражения (2) и (3). Уравнение вида (6) называют уравнением гармонического осциллятора, а колебательную систему, которая совершает эти колебания гармоническим осциллятором (примерами гармонических осцилляторов являются: пружинный маятник, физический маятник, электрический колебательный контур).

Видео:Свободные колебания материальной точки 2Скачать

Представление гармонических колебаний в комплексной форме

Сложение, разложение на составляющие и другие операции при изучении гармонических колебаний проще проводить, если представить уравнение гармонических колебаний в комплексной форме. При этом вместо действительной формы записи (2 и 3) используют комплексную:

Величина $tilde$ является комплексной и не дает реального физического отклонения, которое характеризуется вещественной величиной $s$ (2,3). Но мнимую часть величины $tilde$ можно рассматривать как действительной гармоническое колебание выраженное синусом. С другой стороны действительная часть (7) равная:

представляет собой вещественное гармоническое колебание. Поэтому гармонические колебания можно записывать в комплексном виде (7) и выполнять все требуемые расчёты. При получении результата нужно взять действительную или мнимую часть для перехода к физическим величинам.

Видео:Д1 Дифференциальные уравнения движения материальной точкиСкачать

Примеры задач на колебательное движение

Задание: Материальная точка, массой $m=^$кг совершает колебания согласно закону: $x=0,05$. Каково максимальное значение возвращающей силы, действующей на точку ($F_$)?

Решение:В соответствии со вторым законом Ньютона на материальную точку действует сила:

Так как колебания точки происходят по оси X, то получим:

Вычислим вторую производную от $xleft(tright)=0,05$, имеем:

Подставим правую часть выражения (1.3) в (1.2) вместо соответствующей производной, учитывая массу точки получаем:

Максимальное значение косинуса равно единице, значит:

Ответ: $left|F_right|=2cdot ^$Н

Задание: Нарисуйте траекторию колебательного движения точки, если она участвует одновременно в двух взаимно перпендикулярных колебаниях, которые описывают законы:

Решение:Определим, каким является уравнение колебательного движения точки в плоскости XY. Используем формулу косинуса двойного угла:

Из условия задачи:

Получаем, что $y$ равен:

Ответ: $yleft(xright)=A-frac<^2>$

Видео:Урок 327. Гармонические колебанияСкачать

Дифференциальное уравнение колебательного движения материальной точки дано в виде

Тестовые вопросы по теме «Прямолинейные колебания точки»

— Как называется число полных колебаний, совершаемых за 1 с ?

1. частота колебаний

2. период колебаний

3. фаза колебаний

4. циклическая колебаний

5. амплитуда колебаний

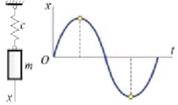
— На рисунке представлен график колебаний. (для справки k — циклическая частота собственных колебаний; b — коэффициент вязкого сопротивления; f — коэффициент сухого трения; p — частота вынуждающей силы)

1. вынужденных при b =0, f =0, p k

2. затухающих при b k , f =0, p =0,

3. затухающих при b > k , f =0, p =0,

4. свободных при b =0, f =0, p =0.

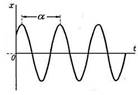
— На представленном рисунке величина обозначенная как « α » — это.

1. период свободных колебаний

2. полупериод свободных колебаний

3. полупериод вынужденных колебаний

4. период вынужденных колебаний

— Данное дифференциальное уравнение d 2 x d t 2 + k 2 x =0 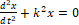является уравнением.

1. вынужденных колебаний без учета сил сопротивления (случай резонанса)

2. свободных колебаний без учета сил сопротивления

3. вынужденных колебаний без учета сил сопротивления

4. вынужденных колебаний с учетом сил сопротивления

5. свободных колебаний с учетом сил сопротивления

— Период колебаний пружинного маятника определяется выражением?

1. 1 2 π m k

2. 2 π m k

3. 2 π k m

4. 1 2 π k m

5. m k

— Частота колебаний пружинного маятника определяется выражением?

1. 1 2 π m k

2. 2 π m k

3. 2 π k m

4. 1 2 π k m

5. m k

— Период колебаний математического мятника определяется выражением?

1. 1 2 π g l

2. 1 π g l

3. 2 π g l

4. 1 2 π l g

5. l g

— Частота колебаний математического маятника определяется выражением ?

1. 1 π g l

2. 2 π l g

3. 1 2 π l g

4. l g

— Дифференциальное уравнение колебательного движения материальной точки дано в виде x 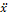+ 10 х = 1,5sin(5 t + 0,4). Если максимальное значение вынуждающей силы равно 60 Н, то масса точки равна…

— На тело, которое подвешено к пружине, действует вертикальная вынуждающая сила F = 30sin20 t. Если угловая частота собственных колебаний тела равна 25 рад/с, то коэффициент динамичности равен…

— Дифференциальное уравнение колебательного движения материальной точки имеет вид x 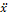+ 36 х = 50sin(5 t + 0,8). Тогда коэффициент динамичности равен…

— На тело массой 3 кг , которое подвешен к пружине, действует вертикальная вынуждающая сила F = 10sin5 t. Если коэффициент динамичности равен 4, то коэффициент жесткости пружины равен…

— На тело массой 50 кг , которое подвешен к пружине, действует вертикальная вынуждающая сила F = 200sin10 t. Если амплитуда вынужденных колебаний равна 0,04 м, то коэффициент жесткости пружины в кН/м равен…

— Дифференциальное уравнение вертикального колебательного движения материальной точки на пружине дано в виде x 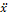+ 16 х = 20sin(6 t + 0,7). Если максимальное значение вынуждающей силы равно 80 Н, то коэффициент жесткости пружины равен…

— Дифференциальное уравнение колебательного движения материальной точки дано в виде 5 x 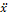+ 320 х = 90sin7 t. Тогда угловая частота собственных колебаний точки равна…

— Статическая деформация пружины, к которой подвешен груз, равна λ = 2 см. Ускорение земного притяжения принять равным 10 м/с 2 . Тогда колебательное движеиие груза описывается дифференциальным уравнением.

1. x +400 x =0 ;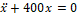

2. x +200 x =0 ;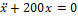

3. x +450 x =0 ;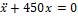

4. x +500 x =0 ;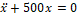

5. x +250 x =0.

— Материальная точка массой 0,6 кг колеблется на вертикальной пружине согласно закону х = 25 + 3sin20 t (см). Тогда в момент времени 2 с модуль реакции пружины равен…

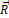
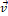
— Материальная точка массой 1 кг колеблется на вертикальной пружине в густой смазке с силой сопротивления R = — 0,1 v . В момент времени, когда ускорение точки равно 14 м/с 2 и скорость точки равна 2 м/с, то реакция пружины равна…

— Груз, подвешенный к пружине, совершает свободные колебания, график которых изображен на рисунке. Начало оси x совпадает с положением центра масс груза при равновесии системы. Начальные условия движения имеют вид.

1. x 0 = x 0 >0, x 0 = V 0 =0 ;

2. x 0 =0, x 0 = V 0 >0 ;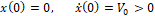

3. x 0 = x 0 x 0 = V 0 =0 ;

4. x 0 =0, x 0 = V 0 ;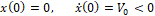

5. x 0 = x 0 >0, x 0 = V 0 >0 .

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

🔍 Видео

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Урок 326. Динамика колебательного движенияСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Дифференциальное уравнение движения материальной точки.Скачать

Дифференциальные уравнения движения материальной точки. Часть 1Скачать

Выполнялка 53.Гармонические колебания.Скачать

Дифференциальные уравнения движения точкиСкачать

Урок 325. Колебательное движение и его характеристикиСкачать

Как решать задачи по динамике материальной точки.Скачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать