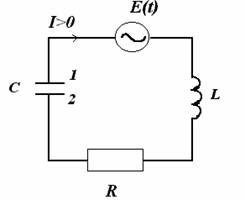
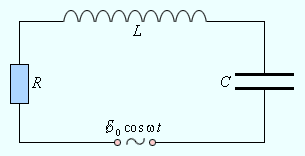
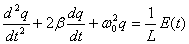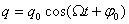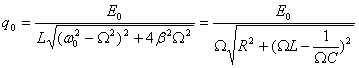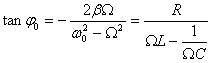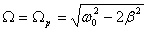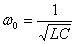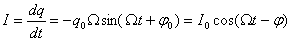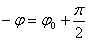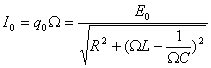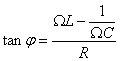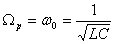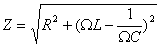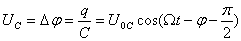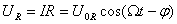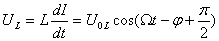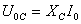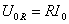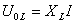Дифференциальное уравнение колебаний заряда на конденсаторе и его решение (8 видео)

Вынужденные электрические колебания

Рассмотрим электромагнитный колебательный контур, в котором помимо ёмкости, индуктивности, сопротивления есть ещё и генератор переменного напряжения, то есть источник электрической энергии. Очевидно, что в таком контуре со временем (это время обычно мало) установятся вынужденные колебания тока с частотой генератора и с постоянной амплитудой; подвод энергии от генератора будет в точности компенсировать потери энергии на сопротивлении.

Не будем учитывать внутреннее сопротивление генератора (будем считать, что у нас хороший, «идеальный» генератор). Получим уравнение для колебаний заряда на обкладках конденсатора. Для этого нам необходимо в закон Ома , который мы писали для затухающих колебаний, добавить в левую часть э.д.с. генератора E(t).

Дифференциальное уравнение вынужденных колебаний заряда в электромагнитном контуре в стандартном (каноническом) виде получается следующим:

или

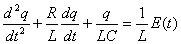
которое полностью аналогично уравнению вынужденных колебаний пружинного маятника . Э.д.с. генератора 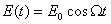. Поэтому сразу можем написать решение:

Резонансная частота колебаний заряда на обкладках конденсатора запишется также по аналогии с резонансной частотой механических колебаний маятника:

Напомню, что в электрическом контуре:

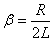
Обратите внимание, что резонансная частота для заряда зависит от коэффициента затухания, а, следовательно, от сопротивления.

Чаще нас интересуют не колебания заряда на конденсаторе, а колебания тока в цепи контура. Найдем эти колебания, продифференцировав заряд по времени:

В этом уравнении сделана подстановка —

Напомню, что — j является сдвигом фазы между напряжением генератора 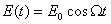и током в цепи. В такой записи знак минус показывает, что напряжение первично, а ток отстает по фазе.

Формулы для амплитуды тока и сдвига фаз выглядят так:

Существенное отличие колебаний тока от колебаний заряда состоит в том, что резонансная частота для тока не зависит от сопротивления; она просто равна собственной частоте свободных колебаний в контуре:

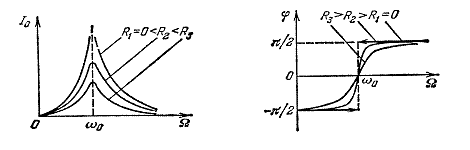
Колебания тока в цепи имеют аналогом не колебания механического маятника, а колебания его скорости. Резонансные кривые для амплитуды тока и зависимость сдвига фаз от частоты для различных сопротивлений — на графиках. Обратите внимание, что при резонансе сдвиг фаз между током и напряжением на генераторе отсутствует.

Посмотрим ещё раз на формулу для амплитуды колебаний тока. В числителе стоит амплитудное напряжение на генераторе (мы пренебрегаем внутренним сопротивлением генератора, поэтому его э.д.с. равна напряжению на его клеммах); в знаменателе — величина, имеющая размерность сопротивления. Она включает в себя не только активное сопротивление R, но и составляющую, зависящую от ёмкости и индуктивности контура и от частоты генератора. Эта величина носит название полного сопротивления контура, или импеданса контура Z:

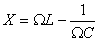
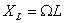
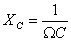
Величина носит название реактивного сопротивления, а её составляющие: — индуктивным сопротивлением; — ёмкостным сопротивлением.

Посмотрим, как ведут себя колебания тока и напряжения на различных участках контура.

Ток в цепи устанавливается со скоростью распространения электрического поля, то есть со скоростью света с. Время установления тока в цепи

l/c, где l — длина контура. Это время в реальных контурах много-много меньше, чем период колебаний. Поэтому мы считаем, что в каждый момент времени значения тока на всех участках цепи одинаково; колебания тока на сопротивлении, индуктивности и ёмкости происходят синхронно.

Иначе обстоит дело с колебаниями напряжения. Вычислим напряжение на каждом элементе контура и посмотрим, как они отличаются по амплитуде и фазе.

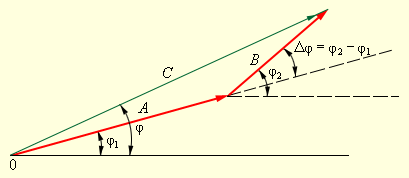
Видно, что напряжение на конденсаторе отстает на четверть периода от напряжения на сопротивлении, а напряжение на индуктивности на столько же по фазе опережает его. Напряжение на ёмкости и индуктивности всегда отличаются по фазе на полпериода. Наглядно сдвиг фаз на элементах цепи можно посмотреть на векторной диаграмме; из неё, в частности, ясно, почему импеданс вычисляется таким образом.

Общее падение напряжения на всех трех элементах цепи равно напряжению на клеммах генератора; поэтому угол j на диаграмме дает сдвиг по фазе между током и напряжением на генераторе.

Содержание

Лекция № 5 Свободные электромагнитные колебания
Вынужденные колебания. Переменный ток
Что такое переменный ток?
Цепи переменного тока
Векторная диаграмма токов и напряжений
Резистор в цепи переменного тока
Конденсатор в цепи переменного тока
Применение элементов высшей математики при решении задач с физическим содержанием
📹 Видео

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Лекция № 5 Свободные электромагнитные колебания

СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ

Выписка из рабочей программы дисциплины «Колебания и волны» – 010900

2.1 Свободные электромагнитные колебания.

Колебательный контур. Процессы в идеализированном колебательном контуре. Электромагнитные гармонические колебания. Дифференциальное уравнение свободных незатухающих электромагнитных колебаний и его решение. Собственная частота свободных электромагнитных колебаний. Формула Томсона. Закон сохранения и превращения энергии в идеализированном колебательном контуре.

1. Свободные электромагнитные колебания

Электромагнитные колебания представляют собой взаимосвязанные периодические изменения зарядов, токов, характеристик электрического и магнитного полей, сопровождающиеся взаимными превращениями этих полей.

Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур – цепь, состоящая из конденсатора ёмкостью и катушки индуктивностью .

Если сопротивление контура равно нулю, колебательный контур называют идеальным. В идеальном колебательном контуре отсутствуют потери энергии, поэтому собственные колебания, возникающие в нем, являются незатухающими.

Рассмотрим процесс возникновения свободных незатухающих колебаний в идеальном колебательном контуре. Чтобы возбудить колебания, необходимо сообщить конденсатору некоторый заряд, а потом замкнуть ключ К (рис.1).

Пусть в начальный момент времени () конденсатору сообщили некоторый заряд . При этом напряжение между его обкладками , напряженность электрического поля и энергия электрического поля – максимальны, а ток в цепи отсутствует (рис. 2,а). Затем начинается разряд конденсатора. Возникающий при этом разрядный ток, проходя через катушку , создает в ней изменяющееся магнитное поле, которое продолжает расти до тех пор, пока ток не достигает максимального значения . При этом вся энергия электрического поля конденсатора переходит в энергию магнитного поля катушки , а индукция магнитного поля достигает максимума (рис. 2,б). Несмотря на то, что конденсатор полностью разрядился, ток в колебательном контуре не прекращается и поддерживается э. д.с. самоиндукции, что в итоге приведет к перезарядке конденсатора. При этом заряд конденсатора, напряжение между обкладками, напряженность и энергия электрического поля вновь достигают максимальных значений, однако полярность обкладок конденсатора и направление напряженности электрического поля между ними противоположны тем, какие были в начальный момент времени (рис. 2, в). По окончании перезарядки энергия магнитного поля катушки перейдет в энергию электрического поля конденсатора. Начиная с этого момента, ток в контуре меняет направление, и процесс воспроизводится в обратном направлении (рис. 2, г). Система возвращается в исходное состояние (рис. 2, д), и начинается следующий период колебаний.

В контуре возникают электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот. Рисунок 2 представляет собой график зависимости заряда конденсатора от времени , , на котором значениям заряда в моменты времени сопоставлены соответствующие состояния колебательного

контура (а; б; в; г; д).

Так как сопротивление контура равно нулю, т. е. нет потерь энергии, такой процесс должен продолжаться бесконечно, а возникающие колебания называются собственными или свободными.

Период собственных незатухающих колебаний в колебательном контуре определяется формулой Томсона

, (5)

а циклическая частота

. (6)

Колебания заряда происходят по гармоническому закону

, (7)

где – максимальный заряд на обкладках конденсатора;

– циклическая частота собственных колебаний;

– начальная фаза.

Дифференциальное уравнение колебаний заряда на конденсаторе и его решение

На рисунках 3 и 4 представлены соответственно идеальный колебательный контур и график зависимости при .

Очевидно, что изменение напряжения между обкладками описывается таким же законом

(8)

где – максимальное напряжение между обкладками конденсатора.

Так как электрический ток характеризует скорость изменения заряда на обкладках конденсатора,

(9)

где – амплитуда силы тока.

Из выражений (7), (8), (9) следует, что колебания заряда (напряжения) и тока в контуре сдвинуты по фазе на , т. е. ток достигает максимального значения в те моменты времени, когда заряд и напряжение на обкладках конденсатора равны нулю, и наоборот. Этот же вывод следует из анализа рис. 2 (а, б, в, г, д).

Идеальный колебательный контур (рис. 3), в котором происходят свободные незатухающие электромагнитные колебания, представляет собой электрическую цепь, состоящую из конденсатора емкостью и катушки индуктивности . Запишем для этого замкнутого контура второе правило Кирхгофа: сумма падений напряжений равна сумме э. д.с., действующих в контуре.

В контуре действует только одна э. д.с. – э. д.с. самоиндукции, следовательно

где – падение напряжения на конденсаторе;

– мгновенное значение заряда на обкладках конденсатора;

Так как , , то дифференциальное уравнение свободных незатухающих электромагнитных колебаний может быть записано в виде

где – собственная циклическая частота контура.

Уравнение колебаний принимает вид

и называется уравнением свободных незатухающих электромагнитных колебаний в дифференциальной форме.

Из математики известно, что решение этого уравнения имеет вид

т. е. соответствует формуле (7) и рис. 4 (при ).

Таким образом, свободные незатухающие электромагнитные колебания являются гармоническими, а их период определяется формулой Томсона:

2. Закон сохранения и превращения энергии в идеализированном колебательном контуре

Исключительно важным является вопрос об энергии гармонических колебаний. С энергетической точки зрения гармоническое колебание представляет собой непрерывный процесс перехода кинетической энергии движущихся частей осциллятора в потенциальную энергию упругого элемента. Полная энергия гармонического осциллятора есть величина постоянная, так как для него потерь нет. Она равна либо максимальной кинетической энергии ( в момент прохождения положения равновесия) , либо максимальной потенциальной энергии (при амплитудном смешении). В задачах используются именно эти энергии, так как с их помощью можно оценить величину амплитуды и частоты собственных колебаний осциллятора.

Расчет энергии W гармонического осциллятора осуществляют стандартным образом. Для механических осцилляторов:

Видео:Урок 355. Затухающие электромагнитные колебания.Скачать

Вынужденные колебания. Переменный ток

Дадим определение понятию вынужденных колебаний.

Вынужденные колебания – это процессы, которые происходят в электрических цепях под воздействием периодического источника тока.

Основным отличием вынужденных колебаний по сравнению с собственными колебаниями в электрических цепях является то, что они являются незатухающими. Неизбежные потери энергии компенсируются за счет внешнего источника периодического воздействия, который не позволяет колебаниям затухать.

Видео:Свободные электромагнитные колебания. 11 класс.Скачать

Что такое переменный ток?

Переменный ток — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.

Рассмотрим случай, когда электрическая цепь способна совершать собственные свободные колебания с некоторой частотой ω 0 . Предположим, что к этой цепи подключен внешний источник, напряжение которого изменяется по гармоническому закону с частотой ω .

Частота свободных колебаний в электрической сети ω 0 будет определяться параметрами этой сети. Вынужденные колебания, которые установятся при подключении внешнего источника ω , будут происходить на частоте этого внешнего источника.

Частота вынужденных колебаний устанавливается не сразу после включения внешнего источника, а спустя некоторое время Δ t . По порядку величины это время будет равно времени затухания свободных колебаний в сети τ .

Видео:Дифференциальные уравнения. 11 класс.Скачать

Цепи переменного тока

Цепи переменного тока – это такие электрические цепи, в которых под воздействием периодического источника тока происходят установившиеся вынужденные колебания.

Рассмотрим устройство колебательного контура, в который включен источник тока с напряжением, изменяющимся по периодическому закону:

e ( t ) = ε 0 cos ω t,

где ε 0 – амплитуда, ω – круговая частота.

Фактически, это будет R L C -цепь.

Рисунок 2 . 3 . 1 . Вынужденные колебания в контуре.

Будем считать, что для изображенной на этом рисунке электрической цепи выполняется условие квазистационарности. Это позволит нам записать закон Ома для мгновенных значений токов и напряжений:

R J + q C + L d J d t = ε 0 c o c ω t.

Величину L d J d t принято называть напряжением на катушке индуктивности. Фактически, это ЭДС самоиндукции катушки, которую мы для простоты вычислений перенесли с противоположным знаком в левую часть уравнения из правой.

Уравнение вынужденных колебаний можно записать в виде:

u R + u C + u L = e ( t ) = ε 0 cos ω t.

где u R ( t ) , u C ( t ) и u L ( t ) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами U R , U C и U L . Напряжения при установившихся вынужденных колебаниях изменяются с частотой внешнего источника переменного тока ω .

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Векторная диаграмма токов и напряжений

Для решения уравнения вынужденных колебаний мы можем использовать достаточно наглядный метод векторных диаграмм. Для этого используем векторную диаграмму, на которой с помощью векторов изобразим колебания определенной заданной частоты ω .

Давайте посмотрим, как построить векторную диаграмму токов и напряжений.

Рисунок 2 . 3 . 2 . Векторная диаграмма, на которой с помощью векторов изображены гармонические колебания A cos ( ω t + φ 1 ) , B cos ( ω t + φ 2 ) и их суммы C cos ( ω t + φ ) .

Наклон векторов к горизонтальной оси определяется фазой колебаний φ 1 и φ 2 , а длины векторов соответствуют амплитудам колебаний A и B . Относительный фазовый сдвиг определяет взаимную ориентацию векторов: ∆ φ = φ 1 — φ 2 . Для того, чтобы построить вектор, изображающий суммарное колебание, нам необходимо использовать правило сложения векторов: C → = A → + B → .

При вынужденных колебаниях в электрической цепи для построения векторной диаграммы напряжений и токов нам необходимо знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для любого участка цепи.

Источник переменного тока может быть подключен к:

катушке индуктивности L ;
резистору с сопротивлением R ;
конденсатору с емкостью С .

Рассмотрим эти три примера подробнее. Будем считать, что напряжение на резисторе, катушке и конденсаторе во всех трех случаях равно напряжению внешнего источника переменного тока.

Резистор в цепи переменного тока

J R R = u R = U R cos ω t ; J R = U R R cos ω t = I R cos ω t

Мы обозначили амплитуду тока, который протекает через резистор, через I R . Соотношение R I R = U R выражает связь между амплитудами тока и напряжения на резисторе. Фазовый сдвиг в этом случае равен нулю. Физическая величина R – это активное сопротивление на резисторе.

Конденсатор в цепи переменного тока

u C = q C = U C cos ω t

J C = d q d t = C d u C d t = C U C ( — ω sin ω t ) = ω C U C cos ω t + π 2 = I C cos ω t + π 2 .

Соотношение между амплитудами тока I C и напряжения U C : 1 ω C I C = U C .

Ток опережает по фазе напряжение на угол π 2 .

Физическая величина X C = 1 ω C — это емкостное сопротивление конденсатора.

Видео:Колебания в электрической цепи и дифференциальные уравненияСкачать

Применение элементов высшей математики при решении задач с физическим содержанием

В курсе средней школы задачи по физике, при решении которых требуется явное применение дифференциального и интегрального исчисления встречаются нечасто и в большинстве своем вызывают значительные затруднения у выпускников. Конечно, формулировки многих из этих задач требуют ответы на вопросы, которые можно легче получить не из явного решения описывающих протекающие в них явления дифференциальных уравнений, а привлекая известные в физике законы сохранения.

Однако, сравнительный анализ различных способов решения заданий, а также умение использовать изученный в курсе алгебры и начал анализа математический аппарат, безусловно пригодятся выпускникам средней школы для продолжения образования в стенах высшей.

Кроме того, весьма важно установление четкой связи в умах учеников между различными ветвями познания окружающего мира, их взаимодополняющего влияния на точность и четкость воссоздаваемой картины реальности. Я полагаю, что задумываться об этом человек должен как можно раньше, для того чтобы в будущей деятельности плодотворно заниматься творческой исследовательской работой.

Для начала рассмотрим задачу №1, предлагавшуюся на вступительных экзаменах в МФТИ , так как её результаты можно будет использовать при решении последующих задач.

Задача 1. В цепи, изображенной на рис.1 , при разомкнутом ключе К заряд на конденсаторе с емкостью С₂ (С₂=С₁/3) равен q₂, а конденсатор с емкостью С₁ не заряжен. Через какое время после замыкания ключа заряд на конденсаторе С₁ будет иметь максимальное значение? Чему будет равен этот заряд? Омическими потерями в катушке с индуктивностью L пренебречь.

Как показывает опыт работы, простая замена преподавателем схемы из двух последовательно соединенных конденсаторов С₁ и С₂ эквивалентным конденсатором хотя бы для расчетов частоты колебаний контура может совершенно запутать учеников, если они предварительно сами не придут к осознанию равносильности такой замены для ответа на некоторые вопросы задачи. Попробуем составить дифференциальное уравнение для описания колебательных явлений в контуре. Хочется отметить, что то, что близкому к радиотехнике человеку кажется очевидным, вызывает кучу вопросов у учеников, и преподаватель не должен оставлять у них ощущения, что какие-то члены в уравнении или, допустим, их знаки появляются из-за случайных догадок, и подробно последовательно остановиться на всех этапах решения.

Обозначим буквами М, N, F соответствующие точки схемы. Изначально на левой пластине конденсатора С₂ был заряд q₂₀, на правой — (-q₂₀).По закону сохранения заряда сумма зарядов на левой пластине конденсатора С₂ правой пластине конденсатора С₁ остается постоянной, так как заряды в эту часть схемы извне не поступают q₁+q₂=q₂₀.

j _M-j _N=q₁/C₁; (1) j _N-j _F=q₂/C₂ (2). Выберем направление тока в цепи против часовой стрелки, при этом заряд q₂ должен уменьшаться.

Падение напряжения на катушке индуктивности IR=j _M-j _F+e _{сам. инд}. По закону электромагнитной индукции e _cам.инд=Так как активное сопротивление катушки индуктивности равно 0, то j _M-j _FСкладывая уравнения (1) и (2),получим j _M-j _F=q₁/C₁+q₂/C₂. Подставляя данное соотношение в (3), мы получим уравнение (4), справедливое для любого момента времени:

q₁/C₁+q₂/C₂— Продифференцируем это уравнение по времени, получим:

учитывая, что мы приходим к дифференциальному уравнению которое является уравнением гармонических колебаний.

Общее решение этого уравнения I(t) = I_max sin(w t+j ), где w 2 =.

Инерционной частью в данной модели являются заряды на конденсаторах q₁ и q₂, которые не могут измениться мгновенно из-за наличия индуктивности в цепи.

В момент замыкания ключа j _M=j _N, так как конденсатор C₁ не заряжен.

j _M-j _F=j _N-j _F=q₂₀/C₂. Скорость изменения тока в начальный момент времени конечна и равна q₂₀/(C₂L)(см.(3)), его значение в этот момент времени также равно 0, откуда в общем уравнении гармонических колебаний находим первую const: j =0, тогда I(t)=I_max sinw t.

w t; так как q₂(0)=q₂₀, то const=, а зависимость величин зарядов конденсаторов от времени имеет вид:

В моменты времени, когда ток в цепи максимален, Поскольку активное сопротивление цепи равно 0, энергия электромагнитного поля в процессе колебаний сохраняется, т.е. в любой момент времени справедливо соотношение

а при максимальном значении тока из этого соотношения получаем: отсюда

Данный результат можно получить и иначе. Найдем равновесное распределение зарядов на конденсаторах, которое отвечает отсутствию протекания тока в цепи. При этом конденсаторы С₁ и С₂ оказываются включенными параллельно друг другу.

U₁=U₂=q_1p/C₁=q_2p/C₂.Сумма же зарядов на конденсаторах равна q₂₀. Из этих условий получаем, чтоВокруг этих положений и осуществляются колебания зарядов на конденсаторах с течением времени, амплитуда же колебаний соответствует величине I_max/w , что позволяет определить I_max.

В нашем конкретном случае Максимальная величина заряда q₁ будет равняться 3q₂₀/2, а достигаться она будет в моменты времени t=T/2+n? T, где Т — период колебаний, а n=0,1,2. На рис.2 приведены зависимости от времени величины зарядов на конденсаторах и тока, протекающего в цепи.

Подробный анализ данной задачи позволяет подойти к решению более сложного задания, предложенного на вступительных экзаменах в МФТИ.

Задача 2. В схеме, предложенной на рисунке, сначала замыкают ключ К₁ и после того, как конденсатор емкостью С₂ полностью зарядится от батареи с ЭДС E , ключ К₁ раз-

мыкают и замыкают ключ К₂. После замыкания ключа К₂ в схеме происходят свободные незатухающие колебания. Когда напряжение на конденсаторе емкостью С₁ достигает максимального значения, в него быстро (за время, малое по сравнению с периодом колебаний) вставляют диэлектрическую пластину, что приводит к увеличению его емкости в e раз.

1)Чему равен начальный ток в цепи после замыкания ключа К₂?

2)Определить максимальный ток в цепи после вставки пластины.

После замыкания ключа К₁ конденсатор С₂ заряжается до напряжения U= E , на его пластинах скапливаются заряды q₂₀ и -q₂₀, q₂₀=UC₂. После размыкания ключа К₁ источник ЭДС не играет роли в дальнейших процессах и промежуточный этап после замыкания ключа К₂ описывается найденными в задаче №1 соотношениями. Из зависимости зарядов q₁ и q₂ от времени следует, что а

За время, малое по сравнению с периодом колебаний, в процессе внесения в конденсатор C₁ диэлектрической пластины заряды на пластинах конденсаторов не могут измениться, т.к. до начала процесса ток в цепи равнялся 0,а максимальную скорость его изменения можно оценить из уравнения (3).

Она конечна, следовательно, сразу после внесения диэлектрической пластины ток в цепи по-прежнему будет равняться 0.

Колебания зарядов на конденсаторах после внесения диэлектрической пластины будут осуществляться около новых равновесных положений, определяемых условиями: Отсюда находим равновесные распределения зарядов: В момент времени, когда система проходит это равновесное положение, ток в цепи достигает своего максимального значения. Найдем величину этого тока из закона сохранения энергии электромагнитного поля в контуре в процессе колебаний после помещения в него диэлектрической пластины.

Данное уравнение относительно I_max является квадратным, одно из его решений I_max=0 соответствует тривиальному случаю отсутствия колебаний в контуре, а после упрощений можно найти и его второе, интересующее нас решение:

Следующие схемы предлагались на экзамене в МФТИ в качестве наиболее сложных задач.

Задача №3. В колебательном контуре, состоящем из двух последовательно соединенных катушек с индуктивностью L₁ и L₂ и конденсатора с емкостью С, происходят свободные незатухающие колебания, при которых амплитуда колебаний тока равна I₀. Когда сила тока в катушке L₁ максимальна, в неё быстро ( за время, малое по сравнению с периодом колебаний) вставляют сердечник, что приводит к увеличению её индуктивности в m раз.

1)Определить максимальное напряжение на конденсаторе до вставки сердечника.

2)Определить максимальное напряжение на конденсаторе после вставки сердечника.

Составим дифференциальное уравнение колебаний, описывающее поведение данной цепи. Все её элементы соединены последовательно, пусть ток , протекающий в цепи, будет i(t), выберем его направление так, как показано на рис.5. Пусть заряд на правой пластине конденсатора q, тогда j _N-j _M=q(t)/C; (1).

Падение напряжения на катушке L₁ равно 0, так как её активное сопротивление равно 0

( колебания в контуре по условию задачи незатухающие.)

Складывая уравнения (2) и (3) и учитывая (1), получаем уравнение (4), справедливое для любого момента времени до вставки сердечника. (4) Продифференцируем его по времени: Данное дифференциальное уравнение показывает, что колебания в контуре происходят по гармоническому закону, а квадрат частоты собственных колебаний равен . Максимальное напряжение на конденсаторе соответствует максимальному заряду на нем; учитывая, что в точках экстремума дифференцируемой функции q(t) её производная обращается в 0, получаем, что ток в этот момент в цепи равен 0.

По закону сохранения электромагнитной энергии в контуре:

, где U_max— максимальное напряжение на конденсаторе до вставки сердечника. Рассмотрим процесс введения в катушку L₁ сердечника. В это время конденсатор полностью разряжен, j _M=j _N.

j _M-j _F+e _{инд 1}=0, j _F-j _N+e _{инд 2}=0, тогда e _{инд 1}+e _{инд 2}=0, т.е. поскольку вставка сердечника происходит быстро и конденсатор всё это время остается незаряженным. Получаем равенство, вытекающее из сохранения магнитного потока в системе: (L₁+L₂) I_{max нач}=(m L₁+L₂)I_{max кон}. Следовательно, к моменту окончания вставки сердечника I_{max кон}= Тогда для максимального напряжения на конденсаторе после вставки сердечника имеем: