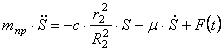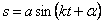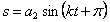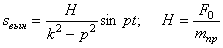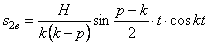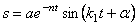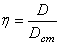Разрешающие дифференциальные уравнения колебаний моста, представленного конечно-элементной моделью, преобразуются к совокупности n типовых обыкновенных дифференциальных уравнений второго порядка /11-12/ относительно обобщённых координат :
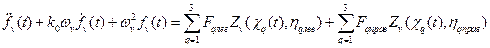
где 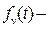




Прогибы ортотропной плиты проезжей части под 

В качестве инертной подвижной нагрузки принят трёхосный самосвал SHACMAN полной массой M=41,0т. При вычислении квазистатической составляющей реакции главных балок пролётного строения на проезд трёхосной подвижной нагрузки использовалось прямое интегрирование уравнений движения с помощью численной пошаговой процедуры методом Ньюмарка. При этом решении подрессоренный автомобиль рассматривался только как силовое воздействие.
Для получения динамической составляющей реакции главных балок от совместного взаимодействия движущегося автомобиля с конструкцией моста, выполнялось совместное решение дифференциальных уравнений для автотранспортного средства (6.1) и для несущей мостовой конструкции (6.2) в программном комплексе Mathcad с использованием встроенной функции, реализующей метод Рунге-Кутта с постоянным шагом интегрирования. Шаг дискретизации по времени 0,005с. Скорость движения трёхосного грузовика принимается постоянной v=16 м/с = 57,6 км/ч. Время движения автомобиля 10,25с. Начальные условия для автомобиля принимаются статическими, для несущих конструкций моста – нулевыми. В расчёте грузовой автомобиль заезжает на разрезное пролётное строение моста начиная с 0,0 с. Изучение колебаний разрезного пролётного строения продолжается и после съезда автомобиля с моста. За время в 3,016с грузовик со скоростью 16 м/с полностью съедет с пролётного строения длиной 43,1м. В расчетах удерживалось из приведенных в табл. 6.1 настоящего раздела отчета пять собственных форм колебаний разрезного пролётного строения моста, наиболее значимые из которых первая изгибная и вторая изгибно-крутильная собственные формы.
Демпфирование для металлического разрезного пролётного строения задавалось постоянным для всех удерживаемых в расчёте собственных форм колебаний. Логарифмический декремент для рассматриваемого металлического пролётного строения моста – δ = 0,06. Параметр затухания колебаний – 

Пробные вычисления динамической реакции моста на проезд автомобиля по абсолютно гладкой и не имеющей неровностей проезжей части показал, что колебания моста практически не возбуждаются. Это приводит к выводу, что влияние изменчивости прогибов (так называемой «обратной» связи), на колебания движущегося автомобиля и на колебания пролетного строения незначительно. Поэтому близкие к имеющим место при натурных динамических испытаниях колебания моста могут быть объяснены влиянием неровностей на проезжей части. Поэтому продолжим расчетное моделирование совместных колебаний моста после учета в разрешающих уравнений автомобиля кинематических возмущений от неровностей на проезжей части.
Рис. 6.24. Схематичное изображение положения проезда подвижной инертной нагрузки
Одиночную неровность в месте стыка соседних разрезных пролётных строений задаём детерминированной функцией в виде впадины. При проезде самосвалов через деформационные швы при натурных динамических испытаниях было зафиксировано, что возникают колебания кузова на частоте около 2,0 Гц. С целью моделирования этого процесса математически, впадину в месте деформационного шва необходимо сделать достаточно широкой, чтобы возбудились колебания кузова. При коротких одиночных неровностях и высоких скоростях движения грузовых автомобилей, колебания кузова не успевают возбудиться. Серия пробных расчётов показала, что ширину одиночной впадины в месте стыка пролётных строений необходимо сделать около 2,0м. Глубина впадины около 30мм.
Рис. 6.25. Расчетная одиночная неровность в начале пролётного строения в виде впадины шириной 2,0м и глубиной 30мм
Рис. 6.26. Расчётные вертикальныеколебания главных балок Б1 и Б2 в середине пролёта при проезде по рассматриваемому металлическому пролётному строению одиночного самосвала SHACMAN
Рис. 6.27. Расчётные спектральные плотности амплитуд вертикальных колебаний при проезде по рассматриваемому металлическому пролётному строению одиночного самосвала SHACMAN
Результаты моделирования совместных колебаний пролетного строения моста и движущегося через одиночную гладкую неровность трехосного автомобиля представлены на рис. 6.26, где изображены графики изменения прогибов главных металлических балок Б1 и Б2 в середине пролета №1 расчетной длиной 42,5м.
Из сопоставления приведенных на рис. 6.26 графиков с полученными при натурных испытаниях моста через реку Хопер и приведенных выше на рис. 6.19, видно, что характер колебаний и амплитудные значения близки. Совпадают также приведенные на рис. 6.20 и 6.27 спектральные плотности экспериментальных и расчетных графиков реакции моста на проезд трехосного автомобиля. Это дает основание считать, что принятые для расчетного моделирования предпосылки отвечают действительным особенностям рассматриваемых колебаний.
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Дифференциальное уравнение колебаний моста имеет вид какие из констант необходимо обнулить
Глава 21. Малые колебания механических систем.
21.1. Колебания систем с одной степенью свободы.
21.1.17. Колебания механической системы описываются дифференциальным уравнением 9q + 4q = 2 sin 2t, где q — обобщенная координата. Совершаются ли вынужденные колебания механической системы в фазе с вынуждающей силой? (Ответ Heт)
21.1.18. Консервативная механическая система совершает резонансные колебания, закон изменения обобщенной координаты q во времени показан на рисунке. Во сколько раз увеличатся ординаты точек огибающей N, если в два раза увеличить амплитуду вынуждающей силы? (Ответ 2)
21.1.19. Колебания механической системы описываются дифференциальным уравнением 2q + 3q = 2 sin 5t, где q — обобщенная координата, м. Определить в мм амплитуду обобщенной координаты вынужденных колебаний. (Ответ 42,6)
21.1.20. Дифференциальное уравнение малых колебаний тела имеет вид Iφ + сl 2 φ = lF. Определить в рад амплитуду вынужденных колебаний тела, если момент инерции его относительно оси вращения I = 6 кг • м 2 , коэффициент жесткости пружины с = 3 кН/м, размер l = 0,5 м, сила F = 10sin6 πt. (Ответ 3,62 • 10 -3 )
21.1.21. Определить декремент колебаний механической системы, если дифференциальное уравнение колебаний этой системы имеет вид 8q + 16q + 800q = 0, где q — обобщенная координата. (Ответ 1,88)
21.1.22. Определить логарифмический декремент колебаний механической системы, если дифференциальное уравнение этой системы имеет вид 15q + 30q + 900q = 0. где q — обобщенная координата. (Ответ 0,818)
21.1.23. Колебания нелинейной механической системы описываются дифференциальным уравнением q + 3sinq + 4q = 0, где q — обобщенная координата. Определить логарифмический декремент малых колебаний системы. (Ответ 7,12)
21.1.24. Дифференциальное уравнение движения механической системы имеет вид 20q + 120q + 720q = 0, где q — обобщенная координата. Будет ли в этом случае движение системы апериодическим? (Ответ Нет)
21.1.25. Движение механической системы описывается дифференциальным уравнением 3q+ 6q + 2q = 0, где q — обобщенная координата. Будет ли это движение апериодическим? (Ответ Да)
21.1.26. Свободные затухающие колебания механической системы описываются дифференциальным уравнением 2q + q + 8q = 0, где q — обобщенная координата. Во сколько раз уменьшится амплитуда колебаний за два периода? (Ответ 4,87)
21.1.27. Определить период свободных затухающих колебаний механической системы, если дифференциальное уравнение колебаний этой системы имеет вид 12q + 48q + 432q = 0, где q — обобщенная координата. (Ответ 1,1)
21.1.28. Свободные затухающие колебания механической системы описываются дифференциальным уравнением 2q + 3q + 5q = 0, где q — обобщенная координата, м. Определить обобщенную координату в момент времени t = 1 с, если в начальный момент времени обобщенная координата q0 = 0, а ее производная q0 = 1 м/с. (Ответ 0,334)
21.1.29. Колебания механической системы описываются дифференциальным уравнением 5q + 10q + 125q = 12 sin 5t, где q — обобщенная координата. Определить фазовый угол установившихся вынужденных колебании. (Ответ 1,57)
21.1.30. Движение механической системы описывается дифференциальным уравнением q + 4q + 9q = 10 sin 3t, где q — обобщенная координата. Во сколько раз уменьшится амплитуда установившихся вынужденных колебаний при увеличении коэффициента сопротивления в 2 раза? (Ответ 2)
21.1.31. Дифференциальное уравнение колебаний механической системы имеет вид 64q + 170q + 3000q = F, где q — обобщенная координата, м; F = 150 sin 8t — вынуждающая сила, Н. Определить амплитуду установившихся вынужденных колебаний. (Ответ 8,59 • 10 -2 )
21.1.32. Определить, во сколько раз уменьшится амплитуда установившихся вынужденных малых колебаний неконсервативной механической системы с одной степенью свободы, если амплитуда гармонической обобщенной вынуждающей силы уменьшится в 3 раза. (Ответ 3)
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Дифференциальное уравнение колебаний моста имеет вид какие из констант необходимо обнулить
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ДИНАМИКЕ
Исследование колебаний механической системы с одной степенью свободы
Эти задачи следующие:
2. Построение расчетной схемы .
Ф ормулировка задачи — это условие ( текст) з адачи. Она осу ществляется руководител ем работ сов местно с испол нителе м.
Рас четная схема — эт о рисунок , на ко тор ом изображены :
а) ра циональ но выбранная система координат;
Математическая моде ль — э то система д иф фере нциальных уравн ений, алгебраических уравнений и на чальн ых условий, описывающих динамическое поведение механической системы.
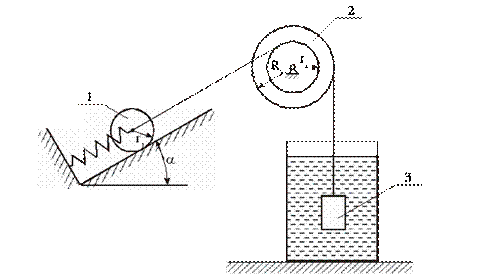
Дано: m1, m2, m3 — массы тел механической системы, с — жесткость упру гого элемента, r 1 — радиус одн ородн ого катка 1, r2, R2 — радиусы ст упеней блока 2, i2 — рад иус инерции блока 2 , 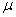
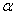
Определить: применяя основные теоремы динамики системы и аналитические методы теоретической механики, определить закон движения первого тела и реакции внешних и внутренних связей. Провести численный анализ полученного решения с использованием ЭВМ.
Порядок выполнения работы:
3) Сформулировать начальные услови я движения.
4) Найти решение дифференциального уравнения движения.
6) По дставив на йденные постоянны е интегрирования в решение дифференциального уравнения, записать закон движ ен ия объ ект а .
8) Построить алгоритм вычис лени й для реализации н а ЭВМ.
9) Произ вес ти вычисления в дисплейном классе.
10) Произв ес ти графическую обработк у результатов вычис лений.
1. Применение основных теорем динамики механической системы
1.1. Постановка второй основной задачи динамики механической системы
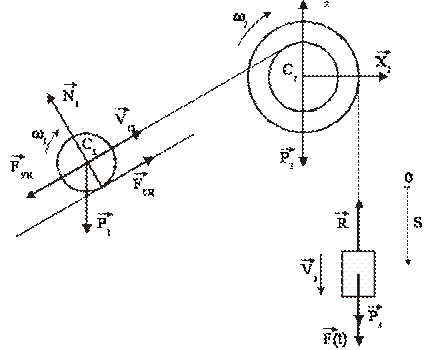
Расчетная схема представлена на рис.2
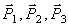
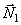
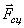
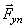
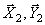
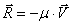
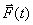
Рассматриваемая механическая система имеет одну степень свободы (нити нерастяжимые, качение катка 1 происходит без скольжения). Будем определять ее положение с помощью координаты S. Начало отсчета координаты совместим с положением статического равновесия центра масс груза 3.
Для пост роения дифферен циального уравнения движен ия с истемы используем теорему об изменении к инетической энергии механической системы в форме:
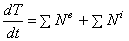
где Т — кинетическая энергия системы,
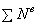
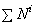
Теорема (1.1) формулируется так: «Производная по времени от кинетической энергии механической системы равн а алгебраической сумме мощностей внеш них и внутренних сил, д ейс твующих на точки механической системы».
Вычислим ки нетическую энергию сис темы как сумму кинетических эн ергий тел 1-3:
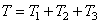
Каток 1 совершает плоскопараллельное движение, поэто му его кинетическая энергия опре деляется по теореме Кенига:
где VC1 – скорость центра масс катка;
JC1 – момент инерции относительно центральной оси катка;
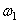
Блок 2 совершает вращ ательное движение около неподвижной оси. Его кинетическая энергия
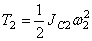
где JC2 – момент инерции относительно центральной оси блока;
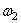
Груз 3 совершает поступательное движение. Его кинетическая энергия равна:
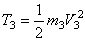
Кинетическая энергия всего механизма будет равна:
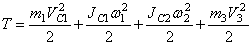
Выразим VC1, 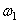
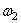
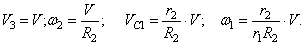
Подставляя (1.3), (1.4), (1.5) в (1.6) с учетом (1.7), получаем:
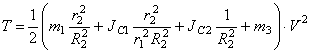
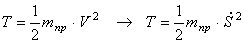
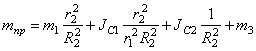
Величину 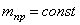
Найдем производную от кинетической энергии по времени
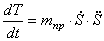
Теперь вычислим правую часть уравнения (1.1) — сумму мощностей внешних и внутренних сил.
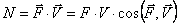
Рассматриваемая нами механическая система является неизменяемой, т.е. тела, входящие в систему, недеформируемы и скорости их точек относительно друг друга равны нулю. Поэтому сумма мощностей всех внутренних сил будет равняться нулю:
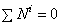
Будут равняться нулю и мощности некоторых внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы
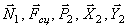
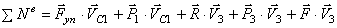
или, раскрывая скалярные произведения,
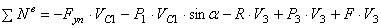
С учетом кинематических соотношений (1.7) сумму мощностей внешних сил преобразуем к виду:
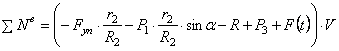
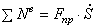
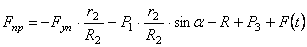
Величину F пр будем называть приведенной силой.
Преобразуем выражение (1.18). Упругую силу считаем пропорциональной удлинению пружины. Полное удлинение пружины f равно сумме статического f ст и динамического SC1 удлинений
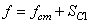
причем из выражения (1.7) для VС1 следует, что 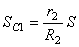
Тогда упругая сила будет равна:

Сила вязкого сопротивления 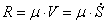
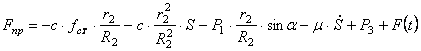
В состоянии покоя приведенная сила равна нулю. Полагая в (1.20) 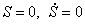
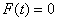
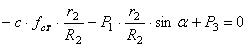
Из уравнения (1.21) определяется статическое удлинение пружины
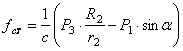
Учитывая (1.22) в (1.20), получаем окончательное выражение для приведенной силы:
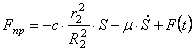
Подставим выражения для производной от кинетической энергии (1.11) и сумму мощностей всех сил (1.17) с учетом (1.23) в уравнение (1.1). Тогда, получаем дифференциальное уравнение движения системы:
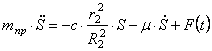
Запишем последнее уравнение в виде:
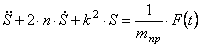
где введены коэффициенты, имеющие определенный физический смысл:
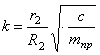
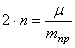
Запишем начальные условия движения:
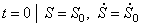
В ыражения (1.25) и (1.26) совместно представляют математическую модель для решения второй задачи динамики.
1.2. Определение закона движения системы.
Проинтегрируем дифференциальное уравнение (1.25). Пусть возмущающая сила изменяется по гармоническому закону:
где 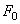
р — циклическая частота возмущения.
Общее решение S неоднородного дифференциального уравнения (1.25) складывается из общего решения однородного уравнения 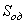
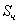
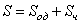
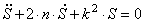
Решение этого уравнения ищем в виде функции
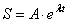
где А и 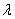
Подставляя (2.3) в (2.2), получаем:
Так как мы ищем нетривиальное решение, то 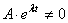
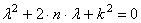
Уравнение (2.4) называется характеристическим уравнением дифференциального уравнения (2.2). Это уравнение имеет два корня:
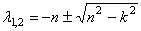
В зависимости от знака подкоренного выражения, корни характеристического уравнения могут быть комплексно-сопряженными или действительными. Возможны три случая:
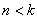
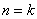
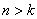
В первом случае ( 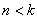
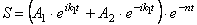
где А 1 , А2 – постоянные интегрирования,
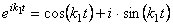
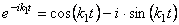
нетрудно представить в виде:
где a , 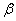
Во втором случае ( 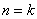
В третьем случае ( 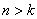
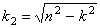
Далее предполагается, что в рассматриваемом примере имеет место случай 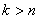
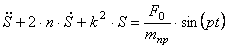
Частное решение ищем в виде правой части

Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева, получаем систему алгебраических уравнений для определения постоянных А и В:
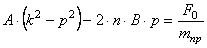
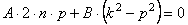
Решая эту систему, получаем следующие выражения для коэффициентов А и В:
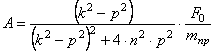
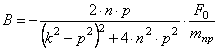
Таким образом, решение (2.12) определено. Складывая (2.8) и (2.12), получаем общее решение неоднородного уравнения (2.11)
Константы а и 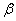
Подчинив (2.14) и (2.15) начальным условиям, получим систему уравнений относительно искомых констант

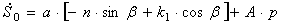
Решая эту систему, получаем:
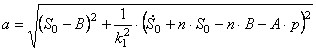
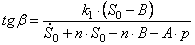
Подставляя (2.16) в (2.14), получаем закон движения механизма.
1.3. Определение реакций внешних и внутренних связей.
Для решения этой задачи расчленяем механизм на отдельные части и изображаем расчетные схемы отдельно для каждого тела (рис.3).
Определение реакций связей проведем с помощью теоремы об изменении количества движения
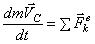
и теоремы об изменении кинетического момента относительно центра масс
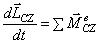
В соответствии с расчетными схемами (рис. 3) записываем уравнения (3.1) и (З.2) в проекциях на оси координат
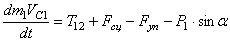
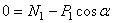


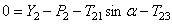
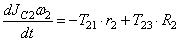
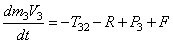
С учетом кинематических соотношений (1.7) систему уравнений (3.3) -(3.9) преобразуем к виду:
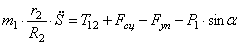
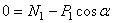
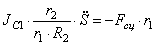

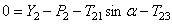
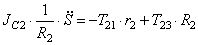
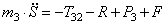
Уравнения (3.10) составляют систему алгебраических уравнений относительно функций
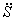
Решая эту систему, получаем и дифференциальное уравнение движения системы, и выражения для определения реакций.
2.1. Составлени е дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа.
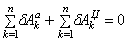
Здесь 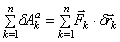

Изобразим на рисунке активные силы и силы инерции (рис.4). Реакции идеальных связей 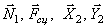
Сообщим системе возможное перемещение. Возможная работа активных сил определяется как сумма следующих элементарных работ:
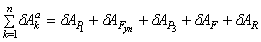
Вычисляя последовательно элементарные работы активных сил и суммируя их, получаем после несложных преобразований
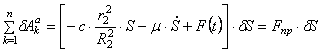
Аналогичное выражение для приведенной силы F пр получено ранее [см. (1.23)].
Найдем возможную работу сил инерции:
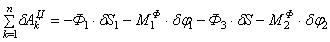
Для величин главных векторов и главных моментов сил инерции имеем следующие выражения:
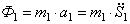
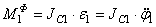

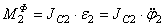
Используя кинематические соотношения (1.7), можно записать
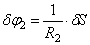
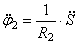
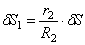
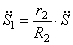
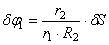
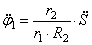
Тогда возможную работу сил инерции можно преобразовать к виду
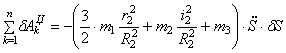
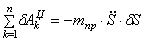
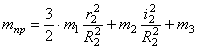
Аналогичное выражение для приведенной массы системы было получено ранее [см.(1.10)]. Подставляя выражения (4.3) и (4.8) в общее уравнение динамики (4.1), получаем
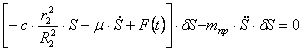
Поделив (4.10) на 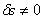

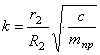
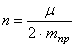
Дифференциальное уравнение (4.11) полностью совпадает с полученным ранее уравнением (1.25).
2.2. Составление дифференциального уравнения движения механизма с помощью уравнений Лагранжа 2— го рода.
Составим теперь уравнения Лагранжа 2-го рода. Для механической системы с одной степенью свободы дифференциальное уравнение движения в обобщенных координатах имеет вид:

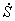
Выражение для кинетической энергии системы было найдено ранее (1.8):
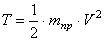
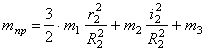
Учитывая, что 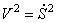
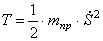
Производные от кинетической энергии
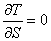
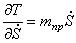
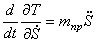
Для определения обобщенной силы Q сообщим системе возможное перемещение 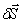
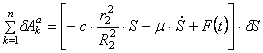
С другой стороны для системы с одной степенью свободы
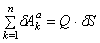
Сравнивая два последних соотношения, получаем
Подставляя производные от кинетической энергии (4.15) и обобщенную силу (4.16) в уравнение Лагранжа, получаем
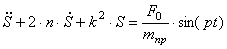
Полученное уравнение (4.18) совпадает с уравнениями (1.25) и (4.11).
3. Анализ колебаний механической системы с одной степенью свободы
3.1. Колебания механической системы при отсутствии сил сопротивления среды
В дифференциальном уравнении движения системы, полученном ранее (1.25), полагаем 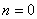
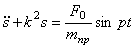
Начальные условия: при 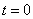
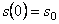
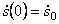
3.1.1. Свободные колебания
Если внешнее возмущение отсутствует (т.е. 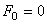
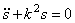
и называется дифференциальным уравнением свободных колебаний, т.е. таких движений системы, которые происходят под действием так называемых восстанавливающих сил. Восстанавливающие силы – это такие силы, каждая из которых стремится вернуть систему в состояние статического равновесия (силы тяжести, упругие силы).
Решение уравнения (5.2) с учетом начальных условий имеет вид:
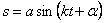
где 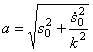
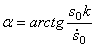
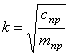
Анализируя решение (5.3) можно сделать следующие выводы:
1. Свободные колебания (рис.5.1) системы с одной степенью свободы представляют собой гармонические колебания.
2. Амплитуда 
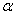
3. Циклическая частота 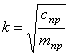
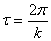
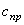
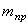
4. Отношения амплитуд колебаний различных точек системы не зависят от начальных условий, так как начальные условия влияют на амплитуды только через множитель 
5. Все точки системы всегда находятся в одной фазе, т.е. они одновременно проходят через свои равновесные положения; координаты всех точек одновременно достигают своих максимальных значений.
3.1.2. Вынужденные колебания
При воздействии возмущающей силы 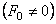
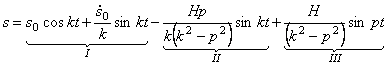
где 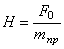
Первые два слагаемых правой части уравнения (5.5):
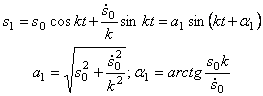
соответствуют свободным колебаниям с частотой 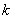
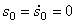
Третье слагаемое в (5.5)
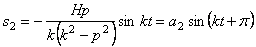
— гармоническое колебание, происходящее с собственной частотой 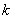
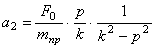
Эти колебания также относятся к свободным колебаниям. Они всегда сопровождают вынужденные колебания при любых начальных условиях, от которых они вообще не зависят.
Их называют сопровождающими колебаниями (рис. 5.2).
Четвертое слагаемое в выражении (4.5):
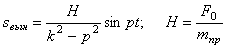
представляет собой вынужденные колебания системы (рис. 5.3).
Таким образом, колебания линейного осциллятора в рассмотренном случае представляют собой линейное наложение трех гармонических колебаний: свободных, сопровождающих и вынужденных (рис. 5.4).
Отметим следующие свойства вынужденных колебаний:
1. Вынужденные колебания происходят с частотой возмущающей силы.
2. Вынужденные колебания не зависят от начальных условий, поэтому для изменения, например, амплитуды (при заданной возмущающей силе) вынужденных колебаний необходимы существенные изменения параметров конструкции: ее жесткости, распределения масс, тогда как в свободных колебаниях для этого достаточно изменить начальные условия.
3. Если 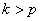
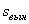
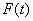
Если 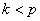
Переписав для этого случая выражение (5.9) в виде:
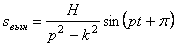
убеждаемся, что при 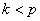
4. Если 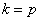
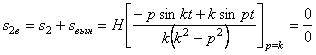
т.е. получим неопределенность, которую можно раскрыть по правилу Лопиталя , заменив дробь в (5.11) пределом
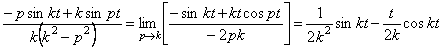
Таким образом, в этом случае общий интеграл (5.5) будет иметь вид:
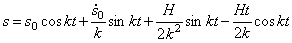
И здесь, как в (5.5) движение осциллятора представляет собой линейное наложение трех колебательных движений, но с одним существенным отличием от (5.5): вынужденные колебания представлены непериодическим слагаемым:
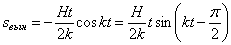
в коэффициенты которого входит время t .
С течением времени он растет по абсолютной величине безгранично, причем вынужденные колебания происходят с возрастающей по линейному закону амплитудой.
Такая ситуация при колебаниях называется резонансом.
5. Если частота вынужденных колебаний не равна частоте свободных колебаний, но близка к ней, то, записав выражение (5.11) в виде:
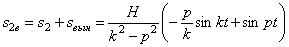
полагаем 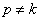
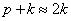
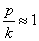
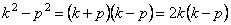
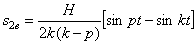
Используя тригонометрическое выражение:
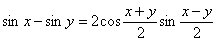

т.е. 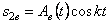
где 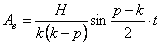
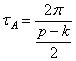
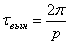
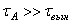
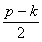
Подобная рассмотренному случаю ситуация представляет собой биение (рис. 5.5).
Таким образом, когда частота вынужденных колебаний весьма близка к частоте свободных (или собственных) колебаний системы, но не равна ей, в колебательной системе возникает биение.
3.2. Колебания механической системы в вязкой среде
Дифференциальное уравнение движения имеет вид (1.25):
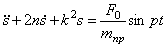
Начальные условия: 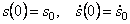
3.2.1. Свободные колебания
Полагая в (5.17) 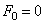
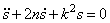
Ограничимся случаем малых сопротивлений и примем 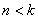
Тогда общее решение однородного уравнения (5.19) с учетом начальных условий можно представить в виде (рис. 5.6):
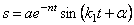
где 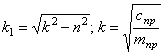

Из закона движения системы (5.20) видно, что в сопротивляющейся среде:
1) свободные колебания являются затухающими;
2) частота затухающих колебаний 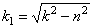
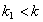
3) амплитуда затухающих колебаний 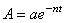
4) период затухающих колебаний 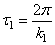
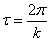
5) отношение любых двух соседних амплитуд: 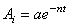
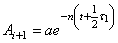
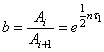
Это отношение называется декрементом затухания. Логарифм этого коэффициента
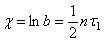
называется логарифмическим декрементом.
Декремент или логарифмический декремент используются для оценки быстроты убывания амплитуды затухающих колебаний.
3.2.2. Вынужденные колебания в сопротивляющейся среде
Дифференциальное уравнение движения в этом случае является неоднородным:
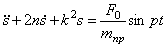
его общее решение имеет вид:
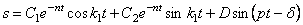
При начальных условиях 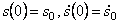
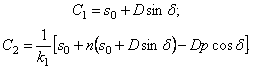
После подстановки постоянных интегрирования (5.27) в общее решение (5.26) получим закон движения механической системы:
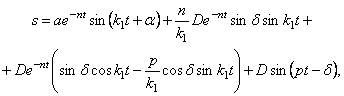
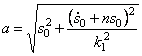
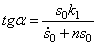
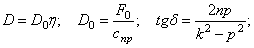
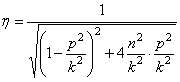
В выражении (5.28) первое слагаемое представляет собой собственные затухающие колебания (рис. 5.6):
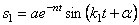
Второе и третье слагаемые в совокупности представляют собой сопровождающие колебания (рис. 5.7):

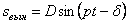
— вынужденные колебания с частотой возмущающей силы (рис. 5.8).
Таким образом, амплитуда вынужденных колебаний при резонансе достигает значительной величины при малых сопротивлениях.
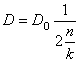
Если 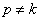
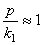
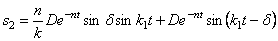
Рассматривая (5.33) и (5.35) совместно и, добавив выражение
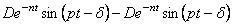
равное нулю, получим закон движения механической системы в виде:
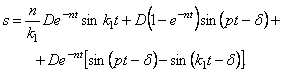
Но выражение в квадратных скобках можно представить так (5.15):
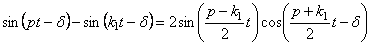
Тогда получим, положив 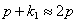

Последнее слагаемое в (5.38) представляет собой колебания биений с затухающей амплитудой
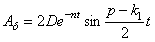
т.е. 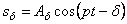
Второе слагаемое в (5.38) – это незатухающие вынужденные колебания
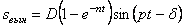
Первое слагаемое в (5.38) – это затухающие сопровождающие колебания
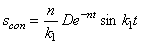
Таким образом, в реальных условиях 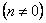
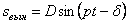
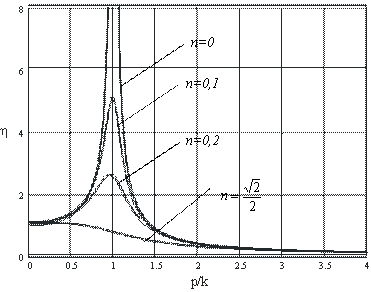
3.3. Коэффициент динамичности
Как было отмечено выше (5.31), коэффициентом динамичности называется отношение максимального динамического отклонения механической системы от положения устойчивого равновесия к статическому отклонению под воздействием силы, равной амплитуде возмущающей силы (рис. 5.10).
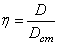
где 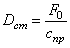
т.е. согласно выражению (5.31):

Максимальное значение 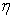
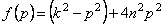
Найдем, при каком значении р функция (5.44) минимальная.
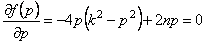
Из (5.45) следует, что
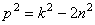
Это возможно, если
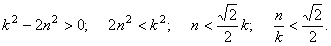
Подставляя (5.46) в (5.43), получаем

При малом значении сопротивления 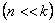
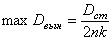
При резонансе 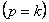

т.е. максимальное значение амплитуды и ее значение при резонансе весьма близки друг к другу (практически одинаковы).
В области, достаточно удаленной от резонанса, при установившемся движении и малом коэффициенте затухания, силами сопротивления можно пренебрегать.
Графические иллюстрации видов колебаний
Рис. 5.1. Собственные колебания
Рис.5.2 Сопровождающие колебания
Рис.5.3 Вынужденные колебания
Рис. 5.4 Результирующие колебания
Рис. 5.5 Биения – результирующие колебания
Колебания в вязкой среде
Рис.5.6. Собственные колебания в вязкой среде
Рис.5.7 Сопровождающие колебания в вязкой среде
Рис. 5.8. Вынужденные колебания
Рис. 5.9 Результирующие колебания в вязкой среде
Рис. 5.10 Коэффициент динамичности
Рис. 5.11. Резонанс ( 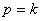
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
📺 Видео
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Дифференциальные уравнения. 11 класс.Скачать

1. Что такое дифференциальное уравнение?Скачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Урок 343. Затухающие колебания (часть 1)Скачать

Урок 327. Гармонические колебанияСкачать

70. Затухающие колебанияСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Однородное дифференциальное уравнениеСкачать

Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать

Дифференциальные уравнения высших порядков, допускающие понижение порядкаСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

4. Однородные дифференциальные уравнения (часть 1)Скачать