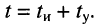Цель работы:
* Знакомство с моделью свободных колебаний в последовательном RLC-контуре.
* Экспериментальное исследование закономерностей свободных незатухающих и затухающих колебаний.
* Экспериментальное определение характеристик затухания в RLC-контуре.
Основные понятия:
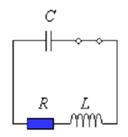
В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур
Закон Ома для замкнутой RLC-цепи, не содержащей внешнего источника тока, записывается в виде
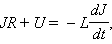
где 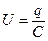

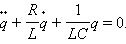
Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда
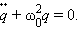
Здесь принято обозначение: 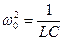
В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону
Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний
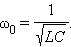
Амплитуда q0 и начальная фаза φ0 определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия.
При свободных колебаниях происходит периодическое превращение электрической энергии Wэ, запасенной в конденсаторе, в магнитную энергию Wм катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:
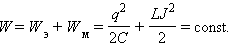
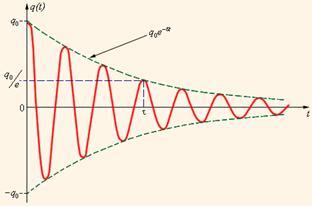
Все реальные контура содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рисунок 2).
Рисунок 2 Затухающие колебания
Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: Fтр = – dυ. Коэффициент d в этой формуле аналогичен сопротивлению R в электрическом контуре. Уравнение свободных колебаний в контуре при наличии затухания имеет вид
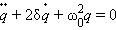
Физическая величина δ = R / 2L называется коэффициентом затухания. Решением этого дифференциального уравнения является функция
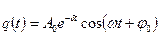
где 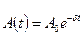
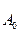
Скорость затухания зависит от электрического сопротивления R контура. Интервал времени 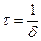
в течение которого амплитуда колебаний уменьшается в e ≈ 2,7 раза, называется временем затухания.
Для характеристики степени затухания в контуре, кроме величины δ, вводят понятие логарифмического декремента затухания q. Он равен натуральному логарифму отношения двух последующих амплитуд (отстоящих во времени на один период)
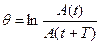
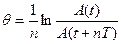

Добротность Q колебательной системы вычисляется:
Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение:
Для RLC-контура добротность Q выражается формулой
Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен.
Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω0 идеального контура с теми же значениями L и C. Но при Q ≥ (5 – 10) этим различием можно пренебречь.
Расчетные формулы:
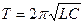
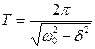
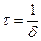
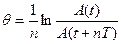
добротность RLC-контура: 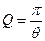
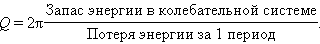
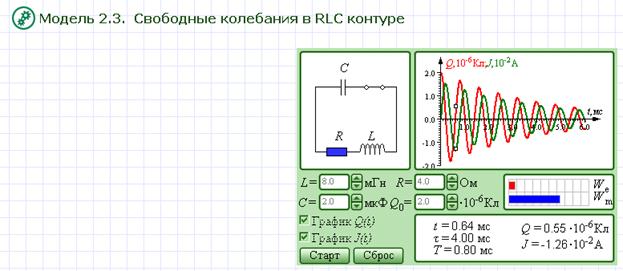
Перейдите от окна теории к окну модели, щелкнув по изображению «Модель. Свободные колебания в RLC-контуре». Внимательно рассмотрите рисунок, найдите все регуляторы и другие основные элементы.
Нажмите кнопку «Старт».Пронаблюдайте картину затухающих колебаний в RLC-контуре. Установите значение R=0. Пронаблюдайте картину незатухающих колебаний. Получите у преподавателя допуск для выполнения измерений.
Порядок измерений и обработка результатов:
ЭКСПЕРИМЕНТ 1. Определение периода затухающих и незатухающих колебаний.
- Установите значение L и C, соответствующее вашей бригаде. Установите значение R=0.
- Выберите график Q(t) (для бригад 1-4), выберите график I(t) (для бригад 5-8), нажмите кнопку «Старт». Нажимая кнопку «Стоп», засеките время n полных колебаний, где n=1 — 7.
- Рассчитайте период колебаний
для каждого значения n. Вычислите среднее значение периода.
- Рассчитайте период колебаний, исходя из параметров RLC-контура
.
- Сравните значения периода, полученные в пп. 3 и 4 со значением периода, выведенным на экране.
- Повторите измерения и расчеты пп. 2-5 для незатухающих колебаний, установив значение R, соответствующее вашей бригаде.
ТАБЛИЦА 1. Параметры RLC-контура (не перерисовывать)
| Бригада |
| L [мГн] |
| C [мкФ] |
| R[Ом] |
ТАБЛИЦА 2. Результаты измерений при L= ____ мГн, C = ____ мкФ, R=0 Ом.
| n | ti, с | 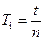 , с , с |
| T ср=____с |
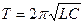
ТАБЛИЦА 3. Результаты измерений при L= ____ мГн, C = ____ мкФ, R=____ Ом.
| n | ti, с | 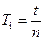 , с , с |
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| T ср=____с |
t =____с, 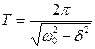
ЭКСПЕРИМЕНТ 2 Определение логарифмического декремента затухания.
- Выберите график q(t).
- Запишите значение
. Измерьте с помощью линейки (или нажимая кнопку «Стоп») амплитуду колебаний через n=3 полных колебаний
.
- Рассчитайте логарифмический декремент затухания
.
- Повторите измерения пп. 2-3 еще 3 раза.
- Рассчитайте среднее значение логарифмического декремента затухания.
- Рассчитайте логарифмический декремент затухания по формуле
.
- Сравните полученные результаты.
ТАБЛИЦА 4. Логарифмический декремент затухания
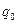 = = 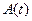 | 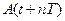 | 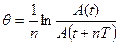 |  |
ЭКСПЕРИМЕНТ 3 Определение добротности контура.
- Определите начальную энергию RLC-контура W0, нажмите кнопку «Старт». Нажимая кнопку «Стоп», определите энергию через одно полное колебание W1.
- Рассчитайте потерю энергии за один период
.
- Рассчитайте добротность
.
- Повторите измерения полной энергии через период W2, W3, W4, W5, каждый раз вычисляя потерю энергии за период
и добротность
- Рассчитайте среднее значение Q.
- Сравните полученный результат с результатом расчетной формулы
.
- Вычислите добротность контура по формуле
ТАБЛИЦА 5. Добротность контура
- RLC-контур. Свободные колебания
- R L C -контур
- Свободные колебания
- Переходные процессы в колебательных контурах
- Свободные колебания в RC-цепи при воздействии видеоимпульса
- Свободные колебания в параллельном контуре без потерь
- Свободные колебания в последовательном RLC-контуре
- Колебания в последовательном RLC-контуре при воздействии в виде отрезка гармонического колебания
- Прохождение радиоимпульса через колебательный контур
- 📹 Видео
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

RLC-контур. Свободные колебания
Видео:Урок 353. Колебательный контурСкачать

R L C -контур
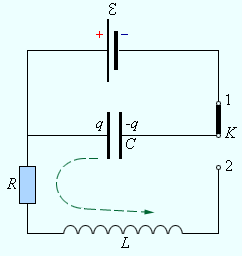
Кроме как в механических системах, к примеру, в таких, маятник или же грузило на пружине, свободные колебания могут возникать также и в электрических цепях, самым простым примером чего может послужить последовательный R L C -контур, изображенный на рис. 2 . 2 . 1 .
Рисунок 2 . 2 . 1 . Последовательный R L C -контур.
Находясь в положении 1 , ключ К позволяет источнику зарядить конденсатор до некоего напряжения δ . Процесс разрядки ранее заряженного конденсатора провоцируется переключением ключа К во второе положение и происходит через катушку индуктивности L и резистор R . При выполнении определенных условий данный процесс может приобретать характер колебательного.
Для не содержащей внешнего источника тока замкнутой R L C -цепи закон Ома представляет из себя выражение:
J R + U = — L d J d t .
В данной формуле U = q C – напряжение на конденсаторе, q является обозначением заряда конденсатора, а J = d q d t – ток в цепи. Правой частью соотношения является выражение ЭДС самоиндукции катушки. В случае, когда заряд конденсатора q ( t ) берется как переменная величина, описывающее свободные колебания в R L C -контуре уравнение может быть приведено к виду:
q · · + R L q · + 1 L C q = 0 .
Для начала рассмотрим такую ситуацию, в которой электромагнитные потери энергии в контуре равны нулю. В таком случае:
q · · + ω 0 2 q = 0 .
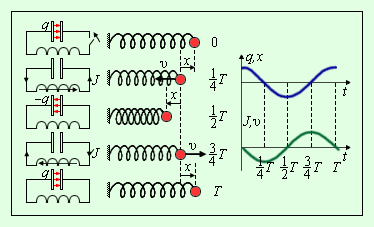
Примем обозначение ω 0 2 = 1 L C . Данным чуть выше уравнением описывается процесс незатухающих свободных колебаний в L C — контуре. Внешне оно полностью эквивалентно уравнению свободных колебаний груза на пружине в условиях отсутствующих сил трения. Аналогичный свободным механическим и электрическим колебаниям процесс изображен на рисунке 2 . 2 . 2 . На данной иллюстрации приводятся графики зависимости заряда смещения x ( t ) груза и q ( t ) конденсатора от положения равновесия, а также графики изменений тока J ( t ) и скорости груза υ ( t ) за период T = 2 π ω 0 колебаний.
Рисунок 2 . 2 . 2 . Аналогия процессов свободных электрических и механических колебаний.
Сделать заключение о некой связи между механическими и электрическими величинами нам позволяет сопоставление процессов в электрическом колебательном контуре и свободных колебаний груза на пружине. Данные аналогии показаны в таблице.
| Электрические величины | Механические величины | ||
| Заряд конденсатора | q ( t ) | Координата | x ( t ) |
| Ток в цепи | J = d q d t | Скорость | ν = d x d t |
| Индуктивность | L | Масса | m |
| Величина, обратная электроемкости | 1 C | Жесткость | k |
| Напряжение на конденсаторе | U = q C | Упругая сила | k x |
| Энергия электрического поля конденсатора | q 2 2 C | Потенциальная энергия пружины | k x 2 2 |
| Магнитная энергия катушки | L I 2 2 | Кинетическая энергия | m ν 2 2 |
| Магнитный поток | L I | Импульс | m υ |
Видео:Свободные электромагнитные колебания. 11 класс.Скачать

Свободные колебания
Свободные колебания в электрическом контуре носят название гармонических при условии отсутствия затухания.
Такие колебания происходят по закону:
q ( t ) = q 0 cos ( ω t + φ 0 ) .
Параметры L и C колебательного контура определяют лишь собственную частоту свободных колебаний:
«Начальными условиями», определяющими амплитуду q 0 и начальную фазу φ 0 , называют тот способ, при помощи которого систему вывели из равновесия.
Например, для процесса колебаний, который начнется в контуре, изображенном на рисунке 2 . 2 . 1 , после перевода ключа K в второе положение, q 0 = C δ , φ 0 = 0 .
Процесс свободных колебаниях провоцирует повторяющееся превращение запасенной в конденсаторе электрической энергии W э в магнитную энергию катушки W м и наоборот. В ситуации, когда потери энергии равны нулю, полная электромагнитная энергия системы не претерпевает изменений:
W = W э + W м = q 2 2 C + L J 2 2 = c o n s t
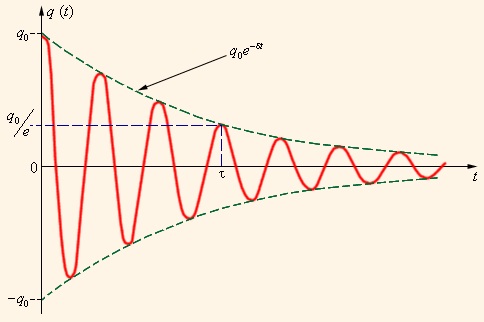
Однако любой реально существующий контур, в отличие от идеального, включает в себя некоторое сопротивление R . По этой причине, процесс свободных колебаний в подобном контуре не подчиняется гармоническому закону. Запасенная в контуре энергия с каждым периодом колебаний теряется, превращаясь в джоулево тепло, из-за чего колебания становятся затухающими (рис. 2 . 2 . 3 ).
Рисунок 2 . 2 . 3 . Затухающие колебания в контуре.
Затухающие колебания в электрическом контуре сравнимы с затухающими колебаниями груза на пружине в условиях существующего вязкого трения, при котором сила трения меняет свое значение прямо пропорционально скорости тела: F т р = – β υ .
В данной формуле сопротивление R электрического контура аналогично коэффициенту β . Уравнение свободных колебаний в контуре при наличии затухания принимает следующий вид:
q · · + 2 δ q · + ω 0 2 q = 0
Коэффициентом затухания называется физическая величина δ = R 2 L .
Следующая функция представляет собой решение приведенного выше дифференциального уравнения:
q ( t ) = q 0 e — δ t cos ( ω t + φ 0 ) ,
Также она содержит описывающий затухание колебаний множитель e x p ( – δ t ) . Скорость затухания зависит от электрического сопротивления R контура.
Интервал времени τ = 1 δ , в течение которого амплитуда колебаний уменьшается в e ≈ 2 , 7 раза, называется временем затухания.
Понятие добротности Q колебательной системы:
где N является числом полных колебаний, которые совершает система за время затухания τ .
Любая добротность Q , относящаяся к колебательной системе, которая способна совершать свободные колебания, имеет следующее энергетическое определение:
Q = 2 π З а п а с э н е р г и и в к о л е б а т е л ь н о й с и с т е м е П о т е р я э н е р г и и з а 1 п е р и о д
Добротность Q , принадлежащая R L C -контуру, выражают формулой:
Добротность электрических контуров, которые применяются в радиотехнике, обычно порядка нескольких десятков и даже сотен.
Стоит обратить внимание на то, что собственная частота ω свободных колебаний в контуре с не самой высокой добротностью несколько уступает собственной частоте ω 0 идеального контура с такими же значениями L и C . Однако при Q ≥ ( 5 ÷ 10 ) данным различием можно пренебречь.
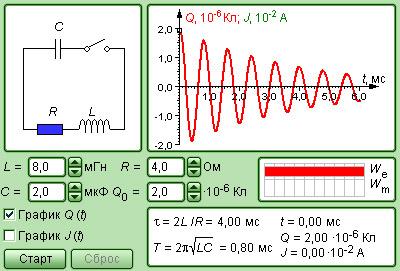
Рисунок 2 . 2 . 4 . Модель свободных колебаний в R L C -контуре.
Видео:RLC контур - вынужденные колебанияСкачать

Переходные процессы в колебательных контурах
Содержание:
Переходные процессы в колебательных контурах:
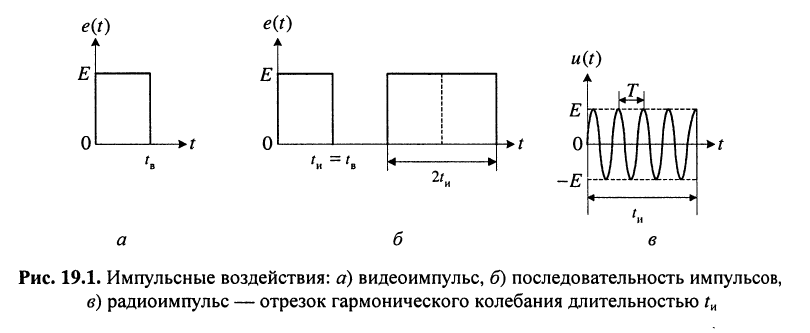
В современных системах телекоммуникации, построенных на принципах цифровой обработки сигналов, сообщения представляются в виде последовательностей одно- или двухполярных импульсов напряжения или тока. Формы импульсов могут быть различными. Здесь рассматриваются только прямоугольные импульсы.
Одиночный прямоугольный импульс с фиксированными длительностью
Импульсы в последовательности могут иметь как строго определённую длительность, так и переменную, обычно кратную длительности одного видеоимпульса
Однако в канал связи собственно импульсы, за редким исключением, не передаются. Они заменяются отрезками гармонического колебания (рис. 19.1, в) длительностью 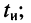
существенно меньше наименьшей длительности импульса 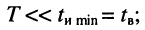
Видео:Билеты №43,44 "Параметры колебательных контуров"Скачать

Свободные колебания в RC-цепи при воздействии видеоимпульса
Задача 19.1.
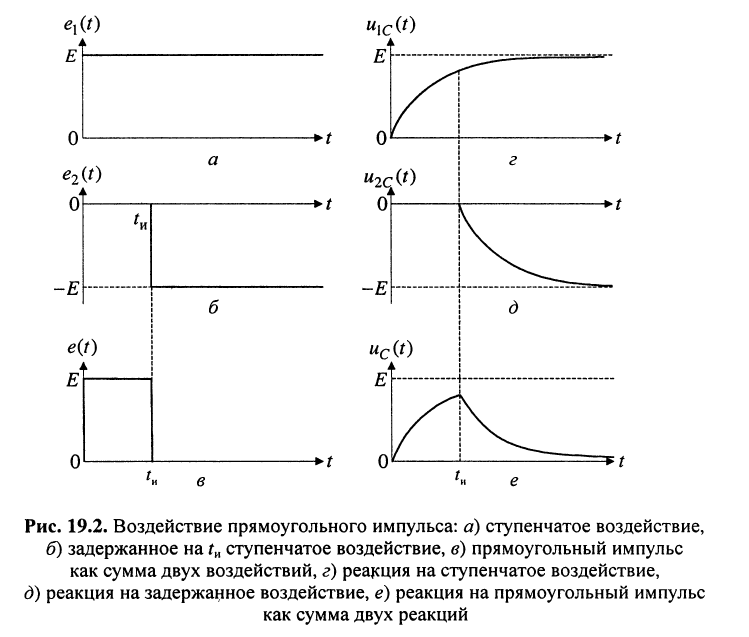
Определить закон изменения напряжения на ёмкости в RС-цепи при воздействии видеоимпульса (рис. 19.2) при нулевых начальных условиях.
Решение. Реакцию на видеоимпульс можно определить, воспользовавшись принципом суперпозиции, а именно: представить видеоимпульс
как сумму двух ступенчатых воздействий одинаковых амплитуд 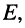
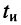
Тогда в силу линейности цепи реакция 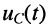
(рис. 19.2, г—е):
где согласно (18.3) имеем:
а реакция запишется как сумма полученных колебаний:
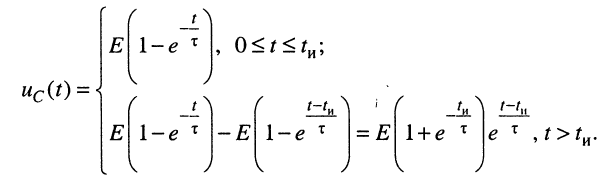
Полученные выражения и рисунок показывают, что за время переходного процесса, ограниченное длительностью видеоимпульса 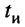
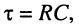
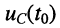
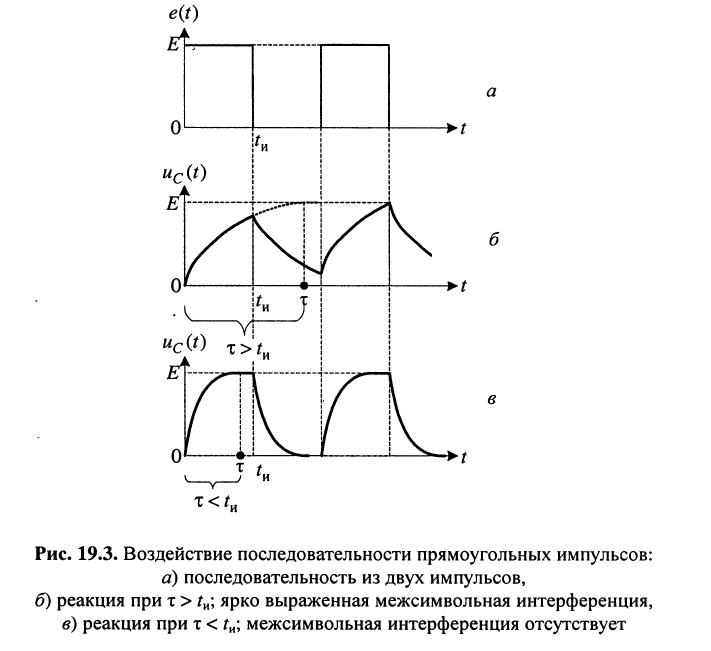
Посмотрим, к чему может привести такое явление при передаче по системе связи не одного, а последовательности импульсов
(рис. 19.3, а), что имеет место в действительности. Если очередной импульс будет передаваться прежде, чем завершится разряд ёмкости1, произойдёт перекрытие, или наложение двух переходных процессов. В результате разряд ёмкости прекратится, и её заряд начнётся не с нуля, а с некоторого напряжения, достигнутого на ёмкости к этому моменту (рис. 19.3, б), т. е. последует частичное перекрытие соседних импульсов во времени, которое приведёт к искажению передаваемых и принимаемых импульсов. Причём от импульса к импульсу искажения будут нарастать.
Искажения такого рода называются межсимвольной интерференцией. Рассмотренное перекрытие соседних импульсов является наиболее простым примером межсимвольной интерференции. Борьба с межсимвольной интерференцией является весьма сложной и актуальной задачей.
Разряд считается завершённым, если напряжение на ёмкости не превышает 0,01 амплитуды Е.
Наиболее остро эта задача стоит перед разработчиками средств современной беспроводной связи, которые весьма широко используются в офисных и домашних сетях передачи информации, в интерфейсах «ноутбук — настольный компьютер», для обеспечения беспроводного доступа в Интернет, для организации сотовой связи. Скорость передачи данных в таких сетях исчисляется в десятках и сотнях гигагерц и имеет тенденцию к дальнейшему её росту.
Для передачи последовательности импульсов с такими скоростями без искажений требуется ряд условий, которые предъявляются к конкретным системам связи и которые изучаются в других дисциплинах.
Добиться исключения межсимвольной интерференции на этапе формирования первичных импульсов и ускорить процесс разряда ёмкости можно, если потребовать, чтобы постоянная времени была не больше длительности видеоимпульса (рис. 19.3, в):
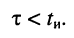
Видео:Урок 347. Вынужденные колебания. Резонанс (часть 1)Скачать

Свободные колебания в параллельном контуре без потерь
Параллельные и последовательные колебательные контуры являются основой избирательных фильтров, амплитудных и фазовых корректоров и входят в состав полосовых усилителей. Свойства перечисленных устройств зависят от свойств колебательных контуров, которые изучим при различных воздействиях.
Задача 19.2.
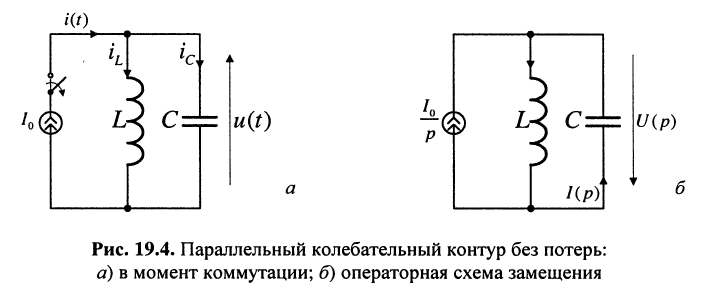
Пусть до момента t = 0 размыкания ключа цепь находилась в режиме постоянного тока: через индуктивность протекал постоянный ток 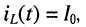
Найти законы изменения тока в контуре 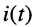
Решение. Для исследования процессов, происходящих в контуре после коммутации, воспользуемся операторным методом и запишем изображение напряжения на контуре:
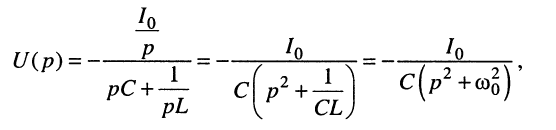
Умножая числитель и знаменатель (19.3) на 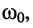
которой соответствует оригинал (см. табл. 16.1, строка № 10):
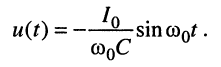
Для определения закона изменения тока в контуре воспользуемся законом Ома в операторной форме
которой соответствует оригинал (см. табл. 16.1 строка № 11):
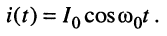
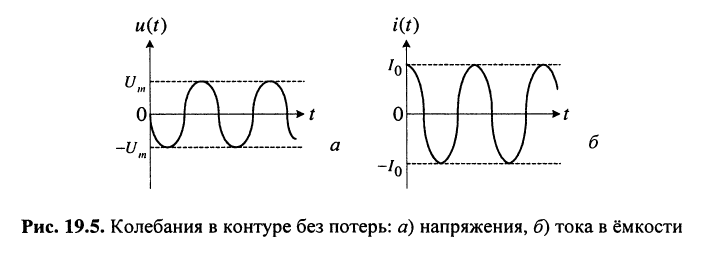
Графики временной зависимости напряжения и тока в контуре без потерь представлены на рис. 19.5.
Заметим, что выражение (19.3) является изображением решения линейного однородного дифференциального уравнения второго порядка, которое описывает процесс свободных колебаний в контуре:
Его характеристическое уравнение
совпадает с характеристическим уравнением выражения (19.3) и имеет пару комплексно сопряжённых мнимых корней
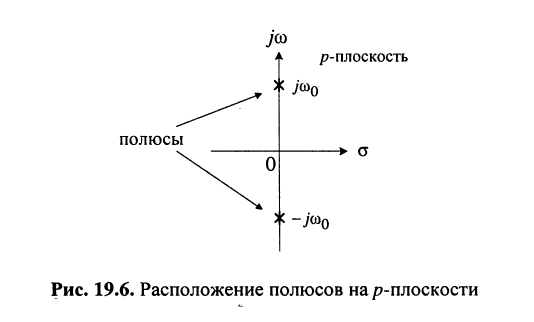
располагающихся на мнимой оси р-плоскости симметрично относительно начала координат (рис. 19.6).
Анализ полученных решений приводит к следующим выводам:
- свободные колебания тока в контуре без потерь и напряжения на его элементах являются отрезками незатухающих гармонических колебаний;
- круговая частота колебаний
.называемая частотой колебаний контура, определяется только параметрами контура L и С и не зависит от начальных условий;
- начальные условия определяют амплитуды колебаний тока
и напряжения
- отношение амплитуд колебаний напряжения и тока в контуре равно его волновому, или характеристическому сопротивлению и не зависит от начальных условий;
- начальные фазы колебаний тока
и напряжения
различны и в общем случае зависят от начальных условий.
Видео:Резонанс в колебательном контуреСкачать

Свободные колебания в последовательном RLC-контуре
Незатухающий характер колебаний в рассмотренном идеальном LC-контуре объясняется отсутствием потерь (т. е. активной проводимости G); в этом случае свободные колебания представляют собой периодический процесс перехода энергии из одного вида в другой: из магнитной в электрическую и обратно. Любой реальный контур содержит не идеальные конденсаторы и катушки индуктивности, что приводит к потерям энергии за счёт её рассеяния (см.разд. 3.3). Наличием потерь обусловлен затухающий характер свободных колебаний, что показывается ниже на примере последовательного колебательного RLС-контура, т. е. контура с потерями, что отражается введением резистивного элемента.
Задача 19.3.
Пусть в момент коммутации t(0) к последовательной RL-цепи (рис. 19.7, а) подключена заряженная ёмкость 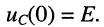
Решение. До коммутации напряжение на ёмкости было равно Е, а ток в индуктивности равнялся нулю. По закону коммутации в образовавшемся RLC-контуре имеем:
Воспользуемся операторной схемой замещения анализируемого контура, для чего, как и в задаче 18.1, представим операторную схему замещения заряженной ёмкости в виде последовательно соединённых источника напряжения 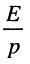
Согласно закону Ома в операторной форме (рис. 19.7, б) изображение реакции (тока) имеет вид:
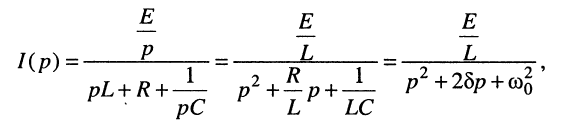
где:
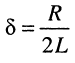
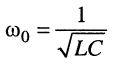
Для оценки характера свободных колебаний обратимся к характеристическому уравнению рассматриваемой цепи, которое получается приравниванием знаменателя (19.6) нулю:
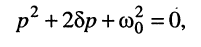
и изучим корни этого уравнения
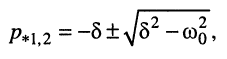
которые являются полюсами функции (19.6).
Поскольку коэффициенты характеристического уравнения вещественны (вследствие вещественности значений параметров R, L и С), его корни (полюсы 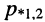
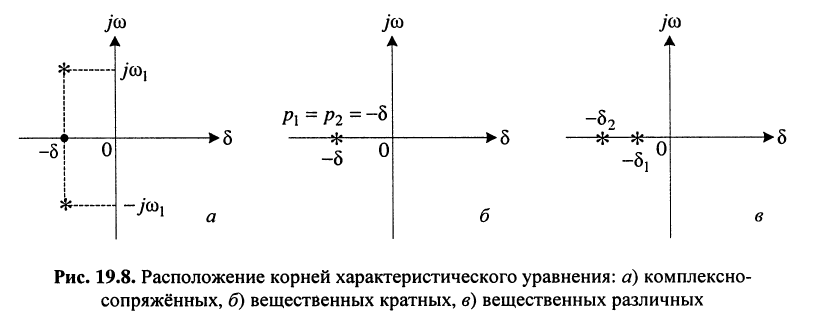
Рассмотрим три возможных случая:
1. Корни (полюсы) комплексно-сопряжённые:
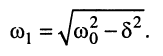
Расположение таких корней на р-плоскости показано на рис. 19.8, а. Такие корни могут быть лишь при условии выполнения неравенства
или, что то же самое, при
Исходя из таблицы соответствий (см. табл. 16.1, строка № 12)
согласно (19.6) получаем формулу для тока в контуре:
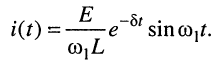
Из последнего выражения видно, что амплитуда колебаний является функцией времени и убывает по экспоненциальному
закону 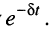
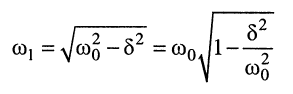
называется частотой собственных затухающих колебаний контура. Она меньше частоты собственных незатухающих колебаний 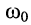
Период затухающих колебаний равен
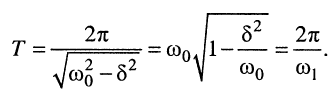
Назовём добротностью контура отношение сопротивления элемента индуктивности к сопротивлению резистивного элемента
тогда коэффициент затухания примет вид:
откуда следует, что колебания в контуре убывают тем медленнее, чем выше добротность контура.
Поскольку частота собственных затухающих колебаний контура (19.9), выраженная через добротность, записывается в виде:
то колебательному режиму в контуре соответствуют значения добротности 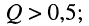
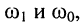
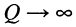
Как говорилось ранее (см. задачу 19.1), процесс свободных колебаний считается оконченным, если амплитуда колебаний становится равной 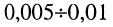
2. Корни характеристического уравнения вещественные кратные.
Если два корня (полюса) равны друг другу 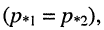
Расположение кратных вещественных корней на р-плоскости показано на рис. 19.8, б. Такие корни согласно (19.8) возможны только при равенстве
т.е. когда
Это — предельный случай колебательного режима, когда частота собственных затухающих колебаний равна нулю:
чему соответствует бесконечно большой период колебаний 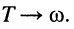
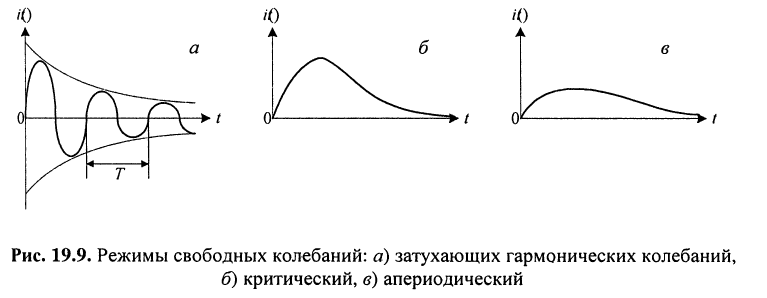
Такой режим свободных колебаний (рис. 19.9, б) называют критическим.
3. Корни вещественные и различные.
Вещественные различные корни можно представить выражением
при условии вещественности
т. е. при 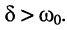
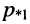
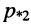
рис. 19.8, в. Следовательно, первичные параметры контура должны удовлетворять неравенству:
Найдём ток в контуре, для чего преобразуем выражение (19.6)
Представим дробь в виде суммы простых дробей
и определим неизвестные коэффициенты разложения 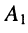
Для равенства левой и правой дробей необходимо, чтобы их числители были равными, поэтому записываем систему уравнений:
из которой нетрудно получить значения искомых коэффициентов:
Подставим найденные коэффициенты разложения в формулу операторного тока:
Для получения формулы протекающего в контуре тока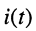
откуда следует, что ток в цепи представляет собой алгебраическую сумму двух экспоненциальных функций, абсолютные значения которых убывают во времени, поскольку корни отрицательны:
Этот режим (рис. 19.9, в) называется апериодическим.
Видео:RLC контур - свободные колебанияСкачать

Колебания в последовательном RLC-контуре при воздействии в виде отрезка гармонического колебания
Задача 19.4.
Пусть при нулевых начальных условиях на последовательный RLC-контур, имеющий резонансную частоту 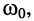
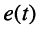
Найти закон изменения тока в контуре.
Решение. Запишем ток в операторной форме согласно закону Ома:
и подставим сюда изображение воздействия
и операторное сопротивление контура
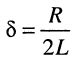
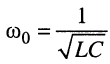
В результате получаем сложную функцию
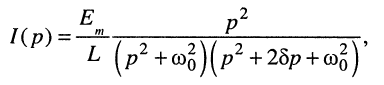
не имеющую табличного соответствия. Для определения оригинала представим (19.13) в виде суммы простых дробей:
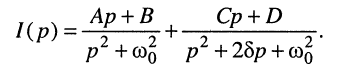
Коэффициенты А, В, С, D определим методом неопределённых коэффициентов, как это было сделано в разд. 19.3.3, для чего приведём дроби (19.14) к общему знаменателю и приравняем числители новой дроби числителю (19.13). После этих несложных преобразований получаем равенство
которое, как нетрудно видеть, справедливо при следующих соотношениях между коэффициентами:
Решение этой системы линейных уравнений даёт:
Подставляя коэффициенты в (19.14), имеем:
Оригиналы для дробей, стоящих в скобках, известны (см. табл. 16.1), и можно сразу записать выражение для тока:
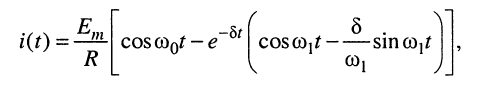
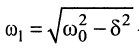
Выражение для тока (19.15) существенно упрощается, если учесть, что на практике применяются контуры высокой добротности 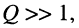
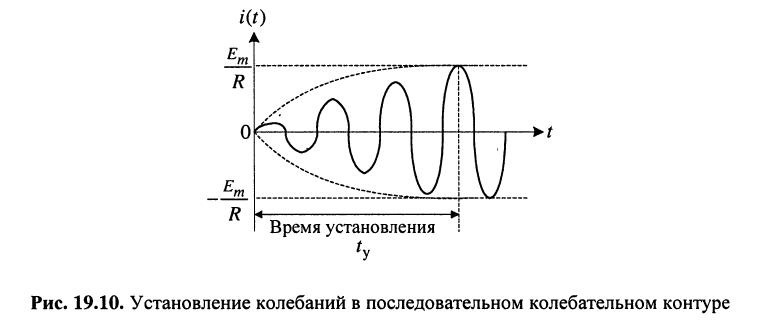
При этих условиях выражение для тока принимает вид:
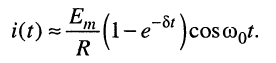
Функция (19.16) описывает колебание (рис. 19.10), которое отличается от гармонического воздействия тем, что его амплитуда возрастает по экспоненциальному закону, стремясь к значению
которое принято называть установившимся.
Из (19.16) следует, что нарастание амплитуды тока происходит тем быстрее, чем больше коэффициент затухания контура 5. Напомним, что процесс установления колебаний в контуре происходит за время
Найдём связь между длительностью переходного процесса 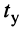
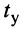
откуда полагают, что
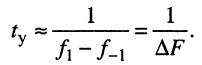
Выводы:
- чем выше добротность контура, т. е. чем уже его полоса пропускания, тем больше длительность переходного процесса, а это, в свою очередь, приводит к большим искажениям формы передаваемого сигнала;
- произведение полосы пропускания контура на длительность переходного процесса в контуре согласно (19.17) приближённо равно единице
; это справедливо и для более сложных избирательных цепей.
Видео:Что такое РЕЗОНАНС НАПРЯЖЕНИЙ | САМОЕ ПОНЯТНОЕ объяснениеСкачать

Прохождение радиоимпульса через колебательный контур
Пусть на контур воздействует радиоимпульс длительности 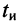
Реакцию контура на радиоимпульс можно найти на основании принципа суперпозиции с учётом полученного в разд. 19.4
решения (19.16).
В зависимости от полосы пропускания контура, т. е. от величины коэффициента затухания контура 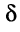
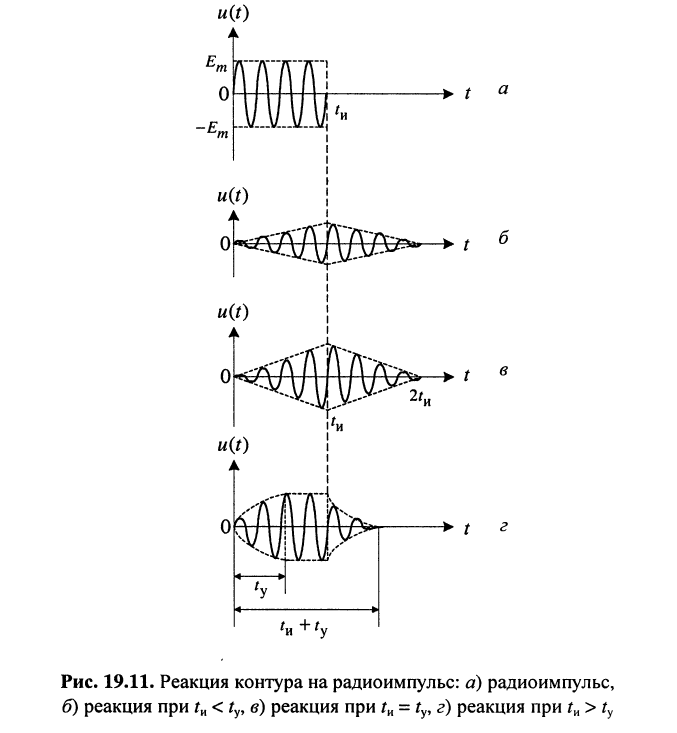
- Длительность радиоимпульса меньше времени установления колебаний:
т.е. полоса пропускания контура достаточно узкая (рис. 19.11,6); импульс значительно искажается, поскольку к моменту окончания воздействия колебания в контуре не являются установившимися.
- Длительность радиоимпульса равна времени установления колебаний — полоса пропускания контура оптимальная (рис. 19.11, в) выполняется соотношение (19.17). В этом случае колебания в контуре могут считаться установившимися к моменту окончания воздействия. Такое же время
потребуется на затухание колебаний в контуре до величины, равной
от установившегося значения. Следовательно, через время
с момента начала воздействия контур будет готов к приёму очередного радиоимпульса.
- Длительность радиоимпульса больше времени установления колебаний:
в этом случае установление колебаний и затухание происходят быстрее (рис. 19.11, г), поэтому очередной радиоимпульс может быть подан на колебательный контур через время
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Расчет переходных процессов
- Классический метод расчета переходных процессов
- Анализ переходных и установившихся процессов методом интеграла свертки
- Операторный метод расчета переходных процессов
- Переходные процессы
- Переходные процессы в линейных цепях
- Переходные процессы в нелинейных цепях
- Переходные процессы в электрических цепях с сосредоточенными параметрами
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📹 Видео
Составление дифференциального уравненияСкачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Урок 354. Математическое описание процессов в колебательном контуреСкачать

Вынужденные электромагнитные колебания. Автоколебания. 11 класс.Скачать

Урок 17. Как работает Интегрирующая и Дифференцирующая RC-цепь | Самое понятное объяснениеСкачать

Колебательный контур. Получение электромагнитных колебаний | Физика 9 класс #45 | ИнфоурокСкачать

Билеты №45 "Вынужденные колебания в линейных системах"Скачать

Урок 355. Затухающие электромагнитные колебания.Скачать

Физика 11 класс (Урок№7 - Свободные и вынужденные электромагнитные колебания. Колебательный контур.)Скачать

Последовательное соединение RLC элементов в цепи синусоидального токаСкачать

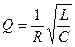
 для каждого значения n. Вычислите среднее значение периода.
для каждого значения n. Вычислите среднее значение периода.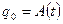 . Измерьте с помощью линейки (или нажимая кнопку «Стоп») амплитуду колебаний через n=3 полных колебаний
. Измерьте с помощью линейки (или нажимая кнопку «Стоп») амплитуду колебаний через n=3 полных колебаний 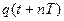 .
.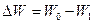 .
.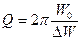 .
.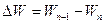 и добротность
и добротность 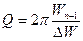
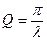 .
.
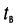
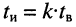
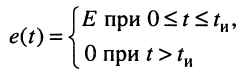
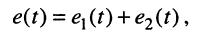
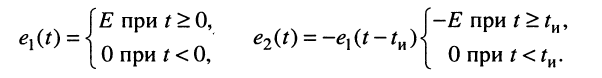
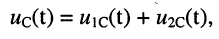
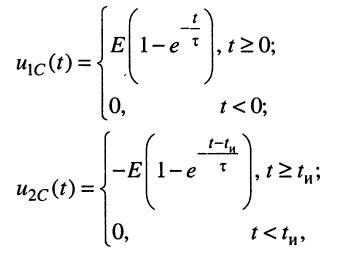

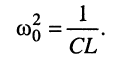
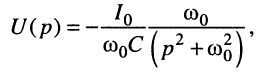
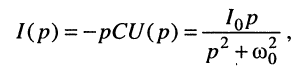
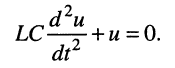
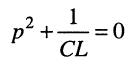
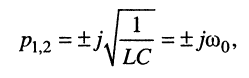
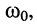 .называемая частотой колебаний контура, определяется только параметрами контура L и С и не зависит от начальных условий;
.называемая частотой колебаний контура, определяется только параметрами контура L и С и не зависит от начальных условий;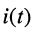 и напряжения
и напряжения 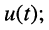
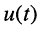 различны и в общем случае зависят от начальных условий.
различны и в общем случае зависят от начальных условий.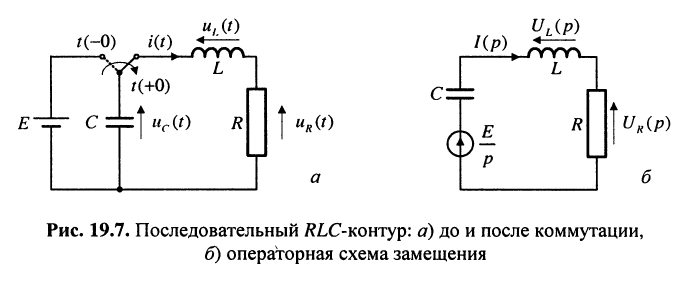

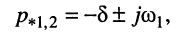
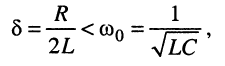
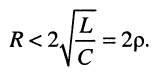
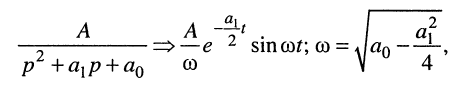
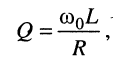
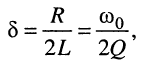
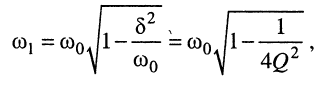

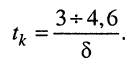
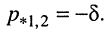
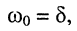
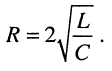
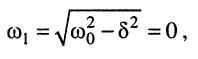
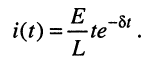
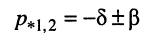
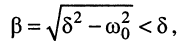
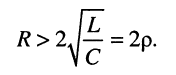
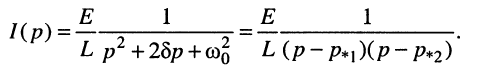
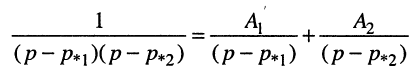
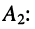
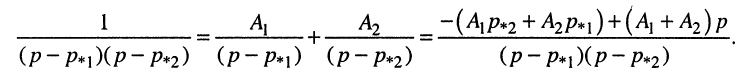
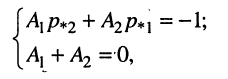
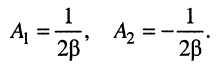
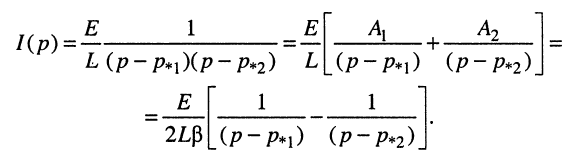
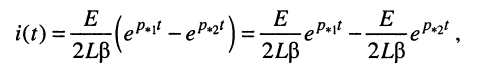
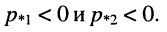
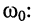
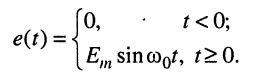
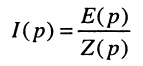
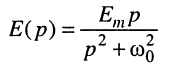
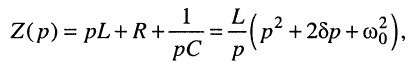
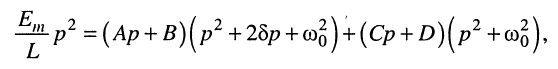
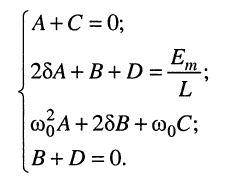
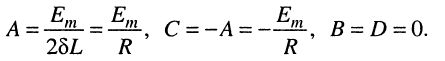
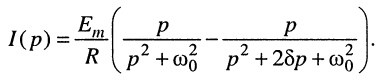
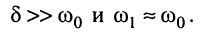
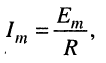
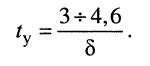
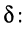
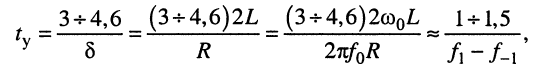
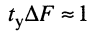 ; это справедливо и для более сложных избирательных цепей.
; это справедливо и для более сложных избирательных цепей.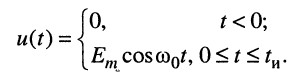
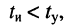 т.е. полоса пропускания контура достаточно узкая (рис. 19.11,6); импульс значительно искажается, поскольку к моменту окончания воздействия колебания в контуре не являются установившимися.
т.е. полоса пропускания контура достаточно узкая (рис. 19.11,6); импульс значительно искажается, поскольку к моменту окончания воздействия колебания в контуре не являются установившимися.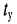 потребуется на затухание колебаний в контуре до величины, равной
потребуется на затухание колебаний в контуре до величины, равной 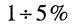 от установившегося значения. Следовательно, через время
от установившегося значения. Следовательно, через время 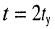 с момента начала воздействия контур будет готов к приёму очередного радиоимпульса.
с момента начала воздействия контур будет готов к приёму очередного радиоимпульса.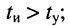 в этом случае установление колебаний и затухание происходят быстрее (рис. 19.11, г), поэтому очередной радиоимпульс может быть подан на колебательный контур через время
в этом случае установление колебаний и затухание происходят быстрее (рис. 19.11, г), поэтому очередной радиоимпульс может быть подан на колебательный контур через время