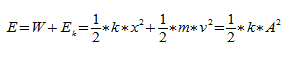Дифференциальное уравнение и закон движения для пружинного маятника в жидкости

§2 Пружинный маятник.

Упругие и квазиупругие силы .

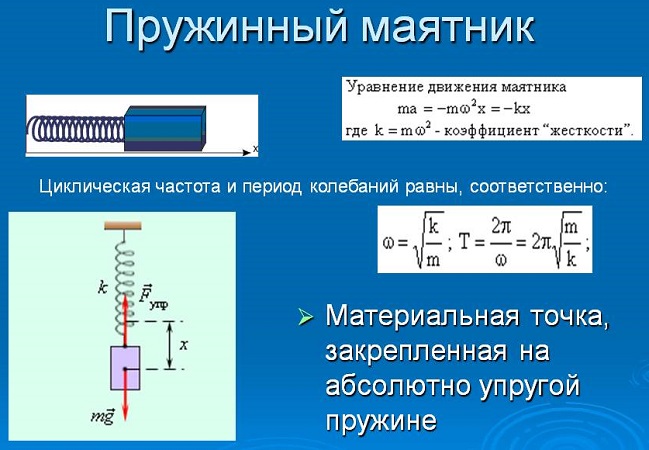
Уравнение колеблющейся пружины

Рассмотрим тело массы m , закрепленное на пружине с коэффициентом жесткости k (массой пружины пренебрегаем). Растянем пружину на х. Тогда по закону Гука на тело будет действовать сила упругости F _упр :

1) величина силы пропорциональна величине отклонения системы от положения равновесия

2) направление сила противоположно направлении смещения, т.е. сила всегда направлена к положению равновесия (при х > 0, F _упр F _упр > 0)

3) В положении равновесия х = 0 и F _упр = 0.

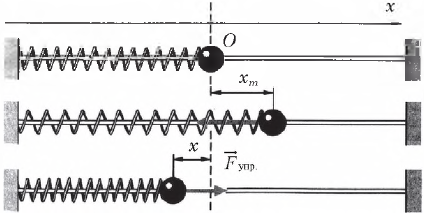
Систему, состоящую из материальной точки массы m и абсолютно упругой пружины с коэффициентом жесткости k , в которой возможны свободные колебания, называют пружинным маятником.

Запишем второй закон Ньютона для рис. б

Если сила не является по своей природе упругой, но подчиняется закону F = — k х , то она называется квазиупругой силой.

Получим уравнение пружинного маятника. Учтем в записи второго закона Ньютона, что

— дифференциальное уравнение точки, совершающей колебательное движение (дифференциальное уравнение пружинного маятника).

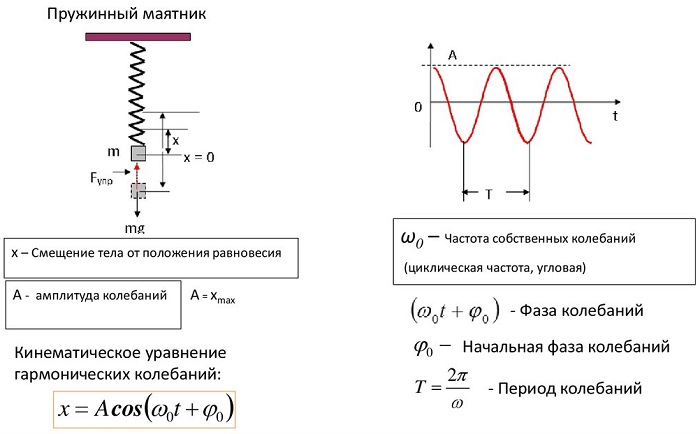
Решение дифференциального уравнения:

— уравнение колеблющейся точки (уравнение колеблющейся пружины).

— собственная частота колебаний.

§3 Математический и физический маятники.

Периоды колебаний математического и физического маятников

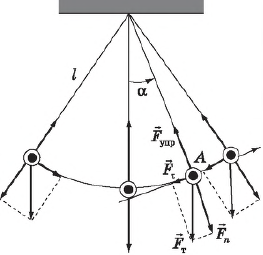
Математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити, и совершавшая колебания в вертикальной плоскости под действием силы тяжести. Материальная точка — тело, масса которого сосредоточена в центре масс и размерами которого в условиях данной задачи, можно пренебречь.

Математический маятник при колебаниях совершает движение по дуге окружности радиуса . Его движение подчиняется законам вращательного движения.

Основное уравнение вращательного цветения запишется в виде

(1)

М – момент сил, I – момент инерции, ε – угловое ускорение.

Равнодействующая сил и равна .

Из треугольника АВС

таким образом, колебания математического маятника происходят под действием квазиупругой силы — силы тяжести.

Тогда (1) запишется в виде

(2)

Знак минус учитывает, что векторы и имеют противоположные направления (угол поворота можно рассматривать, как псевдовектор углового смещения , направление вектора определяется по правилу правого винта, из-за знака минус направлен в противоположную сторону).

Сократив в (2) на m и получим

При малых углах колебаний α = 5 ÷6° , , получим

получим дифференциальное уравнение колебаний математического маятника

— уравнение математического маятника.

из которого видно, что угол α изменяется по закону косинуса. α₀ — амплитуда, ω₀ — циклическая частота, φ₀ — начальная фаза.

— период колебаний математического маятника

Физический маятник — твердое тело, колеблющееся под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через центр тяжести тела, называемой осью качания маятника.

Основное уравнение – вращательного движения для физического маятника запишется в виде

При малых углах колебаний и уравнение движения имеет вид

— дифференциальное уравнение физического маятника.

— период колебаний физического маятника

следовательно, математический маятник с длиной

Видео:Механика. Л 10.1. Колебания. Вывод дифференциального уравнения пружинного маятникаСкачать

Свободные колебания пружинного маятника. Общие сведения

Цель работы. Ознакомиться с основными характеристиками незатухающих и затухающих свободных механических колебаний.

Задача. Определить период собственных колебаний пружинного маятника; проверить линейность зависимости квадрата периода от массы; определить жесткость пружины; определить период затухающих колебаний и логарифмический декремент затухания пружинного маятника.

Приборы и принадлежности. Штатив со шкалой, пружина, набор грузов различной массы, сосуд с водой, секундомер.

1. Свободные колебания пружинного маятника. Общие сведения

Колебаниями называются процессы, в которых периодически изменяется одна или несколько физических величин, описывающих эти процессы. Колебания могут быть описаны различными периодическими функциями времени. Простейшими колебаниями являются гармонические колебания – такие колебания, при которых колеблющаяся величина (например, смещение груза на пружине) изменяется со временем по закону косинуса или синуса. Колебания, возникающие после действия на систему внешней кратковременной силы, называются свободными.

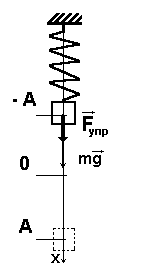
Рассмотрим одну из простейших колебательных систем – пружинный маятник, представляющий собой груз массой m, подвешенный на абсолютно упругой пружине с коэффициентом жесткости k
(рис. 1). Пусть l0 – длина пружины без подвешенного к ней груза. При подвешивании груза под действием силы тяжести пружина растянется на x1 так, что маятник будет находиться в положении равновесия вследствие равенства модулей силы тяжести mg и упругой силы Fупр: mg = kx1, стремящейся вернуть груз в положение равновесия (полагается, что деформации пружины идеально упругие и подчиняются закону Гука).

Если груз вывести из положения равновесия, отклонив на величину x, то сила упругости возрастает: Fупр = – kx2= – k(x1 + x). Дойдя до положения равновесия, груз будет обладать отличной от нуля скоростью и пройдет положение равновесия по инерции. По мере дальнейшего движения будет увеличиваться отклонение от положения равновесия, что приведет к возрастанию силы упругости, и процесс повторится в обратном направлении. Таким образом, колебательное движение системы обусловлено двумя причинами: 1) стремлением тела вернуться в положении равновесия и 2) инерцией, не позволяющей телу мгновенно остановиться в положении равновесия. В отсутствии сил трения колебания продолжались бы сколь угодно долго. Наличие силы трения приводит к тому, что часть энергии колебаний переходит во внутреннюю энергию и колебания постепенно затухают. Такие колебания называются затухающими.

Незатухающие свободные колебания

Сначала рассмотрим колебания пружинного маятника, на который не действуют силы трения – незатухающие свободные колебания. Согласно второму закону Ньютона c учетом знаков проекций на ось X

(1)

Из условия равновесия смещение, вызываемое силой тяжести: . Подставляя в уравнение (1), получим: . Разделив правую и левую часть этого уравнения на m и принимая, что a = d2x/dt2, получим дифференциальное уравнение

. (2)

Это уравнение называется дифференциальным уравнением гармонических колебаний пружинного маятника. Из этого уравнения следует, что после прекращения внешнего воздействия, приводящего к первоначальному отклонению системы от положения равновесия, движение груза обусловлено только действием упругой силы (сила тяжести вызывает постоянное смещение).

Общее решение однородного дифференциального уравнения второго порядка (2) имеет вид

. (3)

Данное уравнение называется уравнением гармонических колебаний. Наибольшее отклонение груза от положения равновесия А0 называется амплитудой колебаний. Величина , стоящая в аргументе косинуса, называется фазой колебания. Постоянная φ0 представляет собой значение фазы в начальный момент времени (t = 0) и называется начальной фазой колебаний. Величина

(4)

есть круговая или циклическая частота собственных колебаний, связанная с периодом колебаний Т соотношением . Период колебаний определяется

. (5)

Рассмотрим свободные колебания пружинного маятника при наличии силы трения (затухающие колебания). В простейшем и вместе с тем наиболее часто встречающемся случае сила трения пропорциональна скорости υ движения:

где r – постоянная, называемая коэффициентом сопротивления. Знак минус показывает, что сила трения и скорость имеют противоположные направления. Уравнение второго закона Ньютона в проекции на ось Х при наличии упругой силы и силы трения

Данное дифференциальное уравнение с учетом υ = dx/dt можно записать

, (8)

где – коэффициент затухания; – циклическая частота свободных незатухающих колебаний данной колебательной системы, т. е. при отсутствии потерь энергии (β = 0). Уравнение (8) называют дифференциальным уравнением затухающих колебаний.

Чтобы получить зависимость смещения x от времени t, необходимо решить дифференциальное уравнение (8). В случае малых затуханий () решение уравнения можно записать следующим образом:

, (9)

где А0 и φ0 – начальная амплитуда и начальная фаза колебаний;
– циклическая частота затухающих колебаний при ω >> ω ≈ ω0.

Движение груза в этом случае можно рассматривать как гармоническое колебание с частотой ω и переменной амплитудой, меняющейся по закону:

. (10)

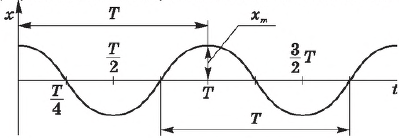
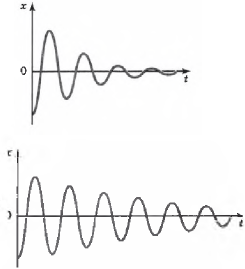
На графике функции (9), рис. 2, пунктирными линиями показано изменение амплитуды (10) затухающих колебаний.

Рис. 2. Зависимость смещения х груза от времени t при наличии силы трения

Для количественной характеристики степени затухания колебаний вводят величину, равную отношению амплитуд, отличающихся на период, и называемую декрементом затухания:

. (11)

Часто используют натуральный логарифм этой величины. Такой параметр называется логарифмическим декрементом затухания:

. (12)

Если за время t‘ амплитуда уменьшается в n раз, то из уравнения (10) следует, что

. (13)

Отсюда для логарифмического декремента получаем выражение

. (14)

Если за время t‘ амплитуда уменьшается в е раз (е = 2,71 – основание натурального логарифма), то система успеет совершить число колебаний

. (15)

Следовательно, логарифмический декремент затухания – величина, обратная числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз. Чем больше θ, тем быстрее происходит затухание колебаний.

2. Методика эксперимента и экспериментальная установка

Рис. 3. Схема установки

Установка состоит из штатива 1 с измерительной шкалой 2. К штативу на пружине 3 подвешиваются грузы 4 различной массы. При изучении затухающих колебаний в задании 2 для усиления затухания используется кольцо 5, которое помещается в прозрачный сосуд 6 с водой.

В задании 1 (выполняется без сосуда с водой и кольца) в первом приближении затуханием колебаний можно пренебречь и считать гармоническими. Как следует из формулы (5) для гармонических колебаний зависимость T 2 = f (m) – линейная, из которой можно определить коэффициент жесткости пружины k по формуле

, (16)

где – угловой коэффициент наклона прямой T 2 от m.

Задание 1. Определение зависимости периода собственных колебаний пружинного маятника от массы груза.

1. Определить период колебаний пружинного маятника при различных значениях массы груза m. Для этого с помощью секундомера для каждого значения m трижды измерить время t полных n колебаний (n ≥10) и по среднему значению времени вычислить период . Результаты занести в табл. 1.

2. По результатам измерений построить график зависимости квадрата периода T2 от массы m. Из углового коэффициента графика определить жесткость пружины k по формуле (16).

Результаты измерений для определения периода собственных колебаний

, с

, с

Видео:Колебания математического маятникаСкачать

Пружинный маятник — формулы и уравнения нахождения величин

Пружинный маятник — колебательная система, которая состоит из тела, подвешенного к пружине. Эта система способна к совершению свободных колебаний.

Подобные системы довольно широко распространены за счет своей функциональной гибкости. Механизмы на основе таких маятников часто используются как элементы средств автоматики.

В том числе они нашли применение в контактных взрывателях различных боеприпасов, в качестве акселерометров в контурах управления ракет. Так же они активно используются в предохранительных клапанах, устанавливаемых в трубопроводах.

Видео:Математические и пружинные маятники. 11 класс.Скачать

Что такое пружинный маятник

Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости.

Приняты следующие обозначения:

k — коэффициент жесткости пружины.

Общий вид маятника:

Особенностями пружинных маятников являются:

Сочетание тела и пружины. Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;

У любой пружины есть исходное положение, предел сжатия и растяжения. При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;

Полная механическая энергия появляется с началом процесса обратимого деформирования. В этот момент на объект не оказывает действие сила упругости;

Колебательные движения происходят под влиянием силы упругости. Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;

От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения. Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.

Видео:Колебания математического и пружинного маятников. 9 класс.Скачать

Виды пружинных маятников

Существует два типа данной системы:

Вертикальный маятник — на тело довольно сильно влияет сила тяжести. Это влияние обуславливает увеличение инерционных движений, которые совершает тело в исходной точке.

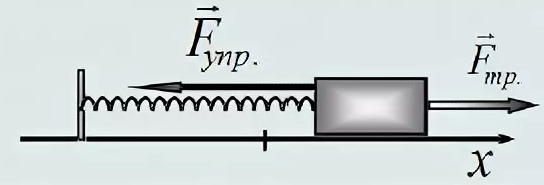
Горизонтальный — в таком варианте при движении на груз начинает действовать сила трения, возникающая по причине того, что груз лежит на поверхности.

Видео:Урок 92 (осн). Колебательное движение. МаятникиСкачать

Сила упругости в пружинном маятнике

До начала деформирования пружина находится в равновесном состоянии. Прикладываемое усилие может как растягивать, так и сжимать её.

Применяя к пружинному маятнику закон сохранения энергии, мы можем рассчитать силу упругости в нем. Упругость прямо пропорциональна расстоянию, на которое сместился груз.

Расчёт силы упругости может быть проведен таким образом:

где k — коэффициент жесткости пружины (Нм),

Видео:Урок 327. Гармонические колебанияСкачать

Уравнения колебаний пружинного маятника

Свободные колебания пружинного маятника описываются с помощью гармонического закона.

Если допустить вероятность того, что колебания идут вдоль оси Х, и при этом выполняется закон Гука, то уравнение примет вид:

F(t) = ma(t) = — mw2x(t),

где w — радиальная частота гармонического колебания.

Для проведения расчета колебаний, учитывая все вероятности, применяют следующие формулы:

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Период и частота свободных колебаний пружинного маятника

При разработке проектов всегда определяется период колебаний и их частота. Для их измерения используются известные в физике формулы.

Изменение циклической частоты покажет формула, приведенная на рисунке:

Факторы, от которых зависит частота:

Коэффициент упругости. На этот коэффициент влияет количество витков, их диаметр, расстояние между ними, длина пружины, жесткость используемого сплава и т. д.

Масса груза. От этого фактора зависит возникающая инерция и скорость перемещения.

Видео:5.4 Уравнение гармонических колебанийСкачать

Амплитуда и начальная фаза пружинного маятника

Учитывая начальные условия и рассчитав уравнение колебаний, можем точно описать колебания пружинного маятника.

В качестве начальных условий используются: амплитуда (А) и начальная фаза колебаний (ϕ).

Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Энергия пружинного маятника

При рассмотрении колебания тел учитывают, что груз движется прямолинейно. Полная механическая энергия тела в каждой точке траектории является константой и равняется сумме его потенциальной энергии и кинетической энергии.

Расчет имеет особенности. При его проведении нужно учитывать несколько условий:

Колебания проходят в двух плоскостях: вертикальной и горизонтальной.

В качестве равновесного положения выбирается ноль потенциальной энергии. Находясь в этом положении пружина сохраняет свою форму.

Влияние силы трения при расчете не учитывают.

Видео:Урок 93 (осн). Исследование пружинного маятникаСкачать

Дифференциальное уравнение гармонических колебаний пружинного маятника

Отметим, что пружинный маятник — это обобщенное определение. Скорость движения груза (тела) напрямую зависит от комплекса условий, в том числе приложенного к нему усилия.

Видео:Период колебаний пружинного маятникаСкачать

Равновесие, закон Паскаля, сила Архимеда, математический и пружинный маятники, механические волны, звук

Видео:Урок 325. Колебательное движение и его характеристикиСкачать

Теория к заданию 4 из ЕГЭ по физике

Равновесие механической системы (абсолютно твердого тела)

Равновесие механической системы — это состояние, при котором все точки механической системы находятся в покое по отношению к рассматриваемой системе отсчета. Если система отсчета инерциальна, равновесие называется абсолютным, если неинерциальна — относительным.

Для нахождения условий равновесия абсолютно твердого тела необходимо мысленно разбить его на большое число достаточно малых элементов, каждый из которых можно представить материальной точкой. Все эти элементы взаимодействуют между собой — эти силы взаимодействия называются внутренними. Помимо этого на ряд точек тела могут действовать внешние силы.

Согласно второму закону Ньютона, чтобы ускорение точки равнялось нулю (а ускорение покоящейся точки равно нулю), геометрическая сумма сил, действующих на эту точку, должна быть равна нулю. Если тело находится в покое, значит, все его точки (элементы) также находятся в покое. Следовательно, для любой точки тела можно записать:

где $↖+↖$ — геометрическая сумма всех внешних и внутренних сил, действующих на $i$-й элемент тела.

Уравнение означает, что для равновесия тела необходимо и достаточно, чтобы геометрическая сумма всех сил, действующих на любой элемент этого тела, была равна нулю.

Из уравнения легко получить первое условие равновесия тела (системы тел). Для этого достаточно просуммировать уравнение по всем элементам тела:

Вторая сумма равна нулю согласно третьему закону Ньютона: векторная сумма всех внутренних сил системы равна нулю, т. к. любой внутренней силе соответствует сила, равная по модулю и противоположная по направлению.

Первым условием равновесия твердого тела (системы тел) является равенство нулю геометрической суммы всех внешних сил, приложенных к телу.

Это условие является необходимым, но не достаточным. В этом легко убедиться, вспомнив о вращающем действии пары сил, геометрическая сумма которых тоже равна нулю.

Вторым условием равновесия твердого тела является равенство нулю суммы моментов всех внешних сил, действующих на тело, относительно любой оси.

Таким образом, условия равновесия твердого тела в случае произвольного числа внешних сил выглядят так:

Закон Паскаля

Гидростатика (от греч. hydor — вода и statos — стоящий) — один из подразделов механики, изучающий равновесие жидкости, а также равновесие твердых тел, частично или полностью погруженных в жидкость.

Закон Паскаля — основной закон гидростатики, согласно которому давление на поверхность жидкости, произведенное внешними силами, передается жидкостью одинаково во всех направлениях.

Этот закон был открыт французским ученым Б. Паскалем в 1653 г. и опубликован в 1663 г.

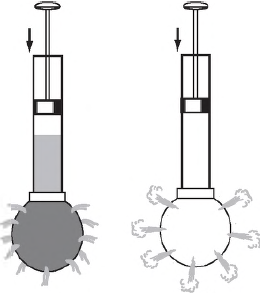
Чтобы убедиться в справедливости закона Паскаля, достаточно проделать простой опыт. Присоединим к трубке с поршнем полый шар со множеством маленьких отверстий. Наполнив шар водой, нажмем на поршень, чтобы увеличить в нем давление. Вода начнет выливаться, но не только через то отверстие, которое находится на линии действия прилагаемой нами силы, а и через все остальные тоже. Причем напор воды, обусловленный внешним давлением, во всех появившихся струйках будет одинаковым.

Аналогичный результат мы получим в том случае, если вместо воды будем использовать дым. Таким образом, закон Паскаля справедлив не только для жидкостей, но и для газов.

Жидкости и газы передают оказываемое на них давление по всем направлениям одинаково.

Передача давления жидкостями и газами во всех направлениях одновременно объясняется достаточно высокой подвижностью частиц, из которых они состоят.

Давление покоящейся жидкости на дно и стенки сосуда (гидростатическое давление)

Жидкости (и газы) передают по всем направлениям не только внешнее давление, но и то давление, которое существует внутри них благодаря весу собственных частей.

Давление, оказываемое покоящейся жидкостью, называется гидростатическим.

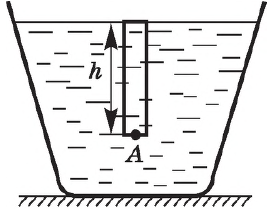
Получим формулу для расчета гидростатического давления жидкости на произвольной глубине $h$ (в окрестности точки А на рисунке).

Сила давления, действующая со стороны вышележащего узкого столба жидкости, может быть выражена двумя способами:

1) как произведение давления $р$ в основании этого столба на площадь его сечения $S$:

2) как вес того же столба жидкости, т. е. произведение массы $m$ жидкости на ускорение свободного падения:

Масса жидкости может быть выражена через ее плотность $р$ и объем $V$:

а объем — через высоту столба и площадь его поперечного сечения:

Подставляя в формулу $F=mg$ значение массы из $m=pV$ и объема из $V=Sh$, получим:

Приравнивая выражения $F=pS$ и $F=pVg=pShg$ для силы давления, получим:

Разделив обе части последнего равенства на площадь $S$, найдем давление жидкости на глубине $h$:

Это и есть формула гидростатического давления.

Гидростатическое давление на любой глубине внутри жидкости не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободного падения и глубины, на которой определяется давление.

Важно еще раз подчеркнуть, что по формуле гидростатического давления можно рассчитывать давление жидкости, налитой в сосуд любой формы, в том числе давление на стенки сосуда, а также давление в любой точке жидкости, направленное снизу вверх, поскольку давление на одной и той же глубине одинаково по всем направлениям.

С учетом атмосферного давления $р_0$, формула для давления покоящейся в ИСО жидкости на глубине $h$ запишется следующим образом:

Гидростатический парадокс

Гидростатический парадокс — явление, заключающееся в том, что вес жидкости, налитой в сосуд, может отличаться от силы давления жидкости на дно сосуда.

В данном случае под словом «парадокс» понимают неожиданное явление, не соответствующее обычным представлениям.

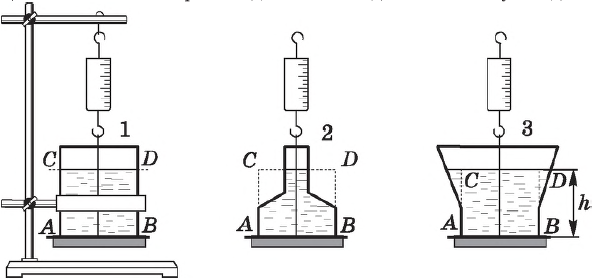
Так, в расширяющихся кверху сосудах сила давления на дно меньше веса жидкости, а в сужающихся — больше. В цилиндрическом сосуде обе силы одинаковы. Если одна и та же жидкость налита до одной и той же высоты в сосуды разной формы, но с одинаковой площадью дна, то, несмотря на разный вес налитой жидкости, сила давления на дно одинакова для всех сосудов и равна весу жидкости в цилиндрическом сосуде.

Это следует из того, что давление покоящейся жидкости зависит только от глубины под свободной поверхностью и от плотности жидкости: $p=pgh$ (формула гидростатического давления). А так как площадь дна у всех сосудов одинакова, то и сила, с которой жидкость давит на дно этих сосудов, одна и та же. Она равна весу вертикального столба $АВСD$ жидкости: $P=pghS$, здесь $S$ — площадь дна (хотя масса, а следовательно, и вес в этих сосудах различны).

Гидростатический парадокс объясняется законом Паскаля — способностью жидкости передавать давление одинаково во всех направлениях.

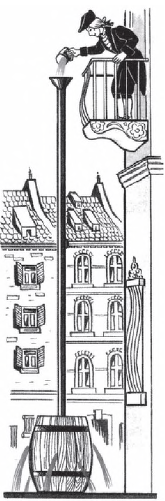
Из формулы гидростатического давления следует, что одно и то же количество воды, находясь в разных сосудах, может оказывать разное давление на дно. Поскольку это давление зависит от высоты столба жидкости, то в узких сосудах оно будет больше, чем в широких. Благодаря этому даже небольшим количеством воды можно создавать очень большое давление. В 1648 г. это очень убедительно продемонстрировал Б. Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, вылил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.

Закон Архимеда

Закон Архимеда — закон статики жидкостей и газов, согласно которому на всякое тело, погруженное в жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа) и направленная по вертикали вверх.

Этот закон был открыт древнегреческим ученым Архимедом в III в. до н. э. Свои исследования Архимед описал в трактате «О плавающих телах», который считается одним из последних его научных трудов.

Ниже приведены выводы, следующие из закона Архимеда.

Действие жидкости и газа на погруженное в них тело

Если погрузить в воду мячик, наполненный воздухом, и отпустить его, то он всплывет. То же самое произойдет со щепкой, с пробкой и многими другими телами. Какая же сила заставляет их всплывать?

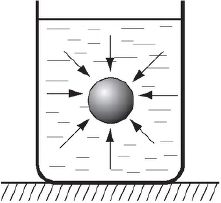
На тело, погруженное в воду, со всех сторон действуют силы давления воды. В каждой точке тела эти силы направлены перпендикулярно его поверхности. Если бы все эти силы были одинаковы, тело испытывало бы лишь всестороннее сжатие. Но на разных глубинах гидростатическое давление различно: оно возрастает с увеличением глубины. Поэтому силы давления, приложенные к нижним участкам тела, оказываются больше сил давления, действующих на тело сверху.

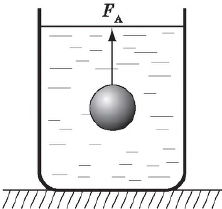
Если заменить все силы давления, приложенные к погруженному в воду телу, одной (результирующей или равнодействующей) силой, оказывающей на тело то же самое действие, что и все эти отдельные силы вместе, то результирующая сила будет направлена вверх. Это и заставляет тело всплывать. Эта сила называется выталкивающей силой, или архимедовой силой (по имени Архимеда, который впервые указал на ее существование и установил, от чего она зависит). На рисунке она обозначена как $F_A$.

Архимедова (выталкивающая) сила действует на тело не только в воде, но и в любой другой жидкости, т. к. в любой жидкости существует гидростатическое давление, разное на разных глубинах. Эта сила действует и в газах, благодаря чему летают воздушные шары и дирижабли.

Благодаря выталкивающей силе вес любого тела, находящегося в воде (или в любой другой жидкости), оказывается меньше, чем в воздухе, а в воздухе меньше, чем в безвоздушном пространстве. В этом легко убедиться, взвесив гирю с помощью учебного пружинного динамометра сначала в воздухе, а затем опустив ее в сосуд с водой.

Уменьшение веса происходит и при переносе тела из вакуума в воздух (или какой-либо другой газ).

Если вес тела в вакууме (например, в сосуде, из которого откачан воздух) равен $Р_0$, то его вес в воздухе равен:

где $F’_A$ — архимедова сила, действующая на данное тело в воздухе. Для большинства тел эта сила ничтожно мала и ею можно пренебречь, т. е. можно считать, что $P_=P_0=mg$.

Вес тела в жидкости уменьшается значительно сильнее, чем в воздухе. Если вес тела в воздухе $P_=P_0$, то вес тела в жидкости равен $Р_= Р_0 — F_A$. Здесь $F_A$ — архимедова сила, действующая в жидкости. Отсюда следует, что

Поэтому чтобы найти архимедову силу, действующую на тело в какой-либо жидкости, нужно это тело взвесить в воздухе и в жидкости. Разность полученных значений и будет архимедовой (выталкивающей) силой.

Другими словами, учитывая формулу $F_A=P_0-P_$, можно сказать:

Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу жидкости, вытесненной этим телом.

Определить архимедову силу можно также теоретически. Для этого предположим, что тело, погруженное в жидкость, состоит из той же жидкости, в которую оно погружено. Мы имеем право это предположить, так как силы давления, действующие на тело, погруженное в жидкость, не зависят от вещества, из которого оно сделано. Тогда приложенная к такому телу архимедова сила $F_A$ будет уравновешена действующей вниз силой тяжести $m_g$ (где $m_$ — масса жидкости в объеме данного тела):

Но сила тяжести $m_g$ равна весу вытесненной жидкости $Р_ж$, Таким образом,

Учитывая, что масса жидкости равна произведению ее плотности $р_ж$ на объем, формулу $F_=m_g$ можно записать в виде:

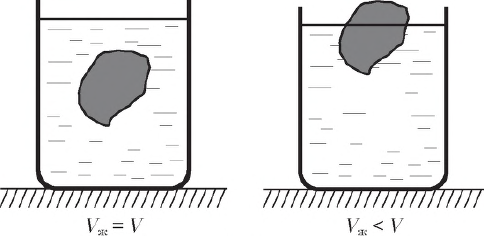
где $V_ж$ — объем вытесненной жидкости. Этот объем равен объему той части тела, которая погружена в жидкость. Если тело погружено в жидкость целиком, то он совпадает с объемом $V$ всего тела; если же тело погружено в жидкость частично, то объем $V_ж$ вытесненной жидкости меньше объема $V$ тела.

С учетом вышеизложенного закон Архимеда можно сформулировать так:

На всякое тело, погруженное в покоящуюся жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная произведению плотности жидкости (или газа), ускорения свободного падения и объема той части тела, которая погружена в жидкость (или газ).

Свободные колебания математического и пружинного маятников

Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинетической) при отсутствии внешних воздействий.

Потенциальная или кинетическая энергия может быть сообщена, например, в механических системах через начальное смещение или начальную скорость.

Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними образуют систему тел, которая называется колебательной системой.

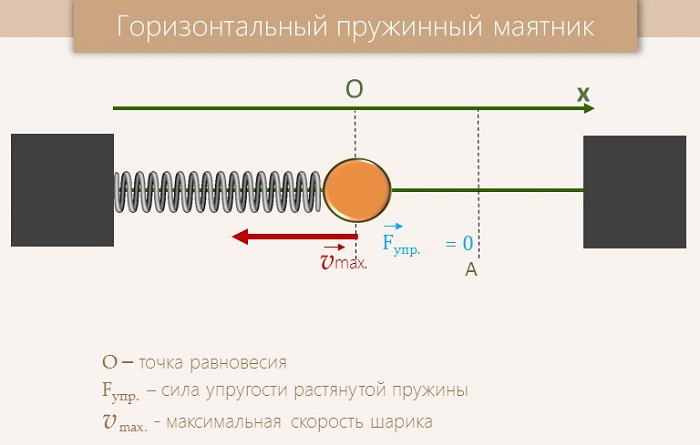
Например, пружина, шарик и вертикальная стойка, к которой прикреплен верхний конец пружины, входят в колебательную систему. Здесь шарик свободно скользит по струне (силы трения пренебрежимо малы). Если отвести шарик вправо и предоставить его самому себе, он будет совершать свободные колебания около положения равновесия (точки О) вследствие действия силы упругости пружины, направленной к положению равновесия.

Другим классическим примером механической колебательной системы является математический маятник. В данном случае шарик совершает свободные колебания под действием двух сил: силы тяжести и силы упругости нити (в колебательную систему входит также Земля). Их равнодействующая направлена к положению равновесия. Силы, действующие между телами колебательной системы, называются внутренними силами. Внешними силами называются силы, действующие на систему со стороны тел, не входящих в нее. С этой точки зрения свободные колебания можно определить как колебания в системе под действием внутренних сил после того, как система выведена из положения равновесия.

Условиями возникновения свободных колебаний являются:

1. возникновение в них силы, возвращающей систему в положение устойчивого равновесия, после того как ее вывели из этого состояния;
2. отсутствие трения в системе.

Динамика свободных колебаний

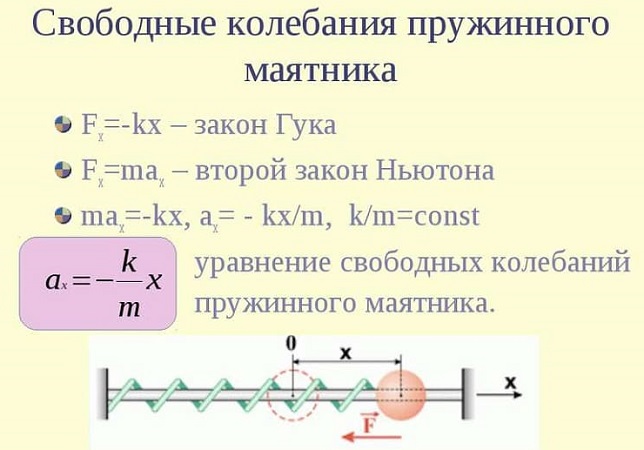
Колебания тела под действием сил упругости. Уравнение колебательного движения тела под действием силы упругости $F_$ может быть получено с учетом второго закона Ньютона ($F=ma$) и закона Гука ($F_=-kx$), где $m$ — масса шарика, $а$ — ускорение, приобретаемое шариком под действием силы упругости, $k$ — коэффициент жесткости пружины, $х$ — смещение тела от положения равновесия (оба уравнения записаны в проекции на горизонтальную ось $Ох$). Приравнивая правые части этих уравнений и учитывая, что ускорение $а$ — это вторая производная от координаты $х$ (смещения), получим:

Это дифференциальное уравнение движения тела, колеблющегося под действием силы упругости: вторая производная координаты по времени <ускорение тела) прямо пропорциональна его координате, взятой с противоположным знаком.

Колебания математического маятника. Для получения уравнения колебания математического маятника необходимо разложить силу тяжести $F_т=mg$ на нормальную $F_n$ (направленную вдоль нити) и тангенциальную $F_τ$ (касательную к траектории движения шарика — окружности) составляющие. Нормальная составляющая силы тяжести $F_n$ и сила упругости нити $F_$ в сумме сообщают маятнику центростремительное ускорение, не влияющее на величину скорости, а лишь меняющее ее направление, а тангенциальная составляющая $F_τ$ является той силой, которая возвращает шарик в положение равновесия и заставляет его совершать колебательные движения. Используя, как и в предыдущем случае, закон Ньютона для тангенциального ускорения — $ma_τ=F_τ$ и учитывая, что $F_τ=-mgsinα$, получим:

Знак минус появился потому, что сила и угол отклонения от положения равновесия $α$ имеют противоположные знаки. Для малых углов отклонения $sinα≈α$. В свою очередь, $α=/$, где $s$ — дуга $ОА$, $l$ — длина нити. Учитывая, что $a_τ=s»$, окончательно получим:

Вид уравнения $s»=/s$ аналогичен уравнению $x»=-/x$. Только здесь параметрами системы являются длина нити и ускорение свободного падения, а не жесткость пружины и масса шарика; роль координаты играет длина дуги (т. е. пройденный путь, как и в первом случае).

Таким образом, свободные колебания описываются уравнениями одного вида (подчиняются одним и тем же законам) независимо от физической природы сил, вызывающих эти колебания.

Решением уравнений $x»=-/x$ и $s»=/s$ является функция вида:

То есть координата тела, совершающего свободные колебания, меняется с течением времени по закону косинуса или синуса, и, следовательно, эти колебания являются гармоническими.

В уравнении $x=x_cosω_t$ хт— амплитуда колебания, $ω_$ — собственная циклическая (круговая) частота колебаний.

Циклическая частота и период свободных гармонических колебаний определяются свойствами системы. Так, для колебаний тела, прикрепленного к пружине, справедливы соотношения:

Собственная частота тем больше, чем больше жесткость пружины или меньше масса груза, что вполне подтверждается опытом.

Для математического маятника выполняются равенства:

Эта формула была впервые получена и проверена на опыте голландским ученым Гюйгенсом (современником Ньютона).

Период колебаний возрастает с увеличением длины маятника и не зависит от его массы.

Следует особо обратить внимание на то, что гармонические колебания являются строго периодическими (т. к. подчиняются закону синуса или косинуса) и даже для математического маятника, являющегося идеализацией реального (физического) маятника, возможны только при малых углах колебания. Если углы отклонения велики, смещение груза не будет пропорционально углу отклонения (синусу угла) и ускорение не будет пропорционально смещению.

Скорость и ускорение тела, совершающего свободные колебания, также будут совершать гармонические колебания. Беря производную по времени функции $x=x_cosω_t$, получим выражение для скорости:

где $υ_$ — амплитуда скорости.

Аналогично выражение для ускорения а получим, дифференцируя $x’=υ=-x_·sinω_t=υ_cos(ω_t+/)$:

где $a_m$ — амплитуда ускорения. Таким образом, из полученных уравнений следует, что амплитуда скорости гармонических колебаний пропорциональна частоте, а амплитуда ускорения — квадрату частоты колебания:

Фаза колебаний

Фаза колебаний — это аргумент периодически изменяющейся функции, описывающей колебательный или волновой процесс.

Для гармонических колебаний

где $φ=ωt+φ_0$ — фаза колебания, $А$ — амплитуда, $ω$ — круговая частота, $t$ — время, $φ_0$ — начальная (фиксированная) фаза колебания: в момент времени $t=0$ $φ=φ_0$. Фаза выражается в радианах.

Фаза гармонического колебания при постоянной амплитуде определяет не только координату колеблющегося тела в любой момент времени, но и скорость и ускорение, которые тоже изменяются по гармоническому закону (скорость и ускорение гармонических колебаний — это первая и вторая производные по времени функции $X(t)=Acos(ωt+φ_0)$, которые, как известно, снова дают синус и косинус). Поэтому можно сказать, что фаза определяет при заданной амплитуде состояние колебательной системы в любой момент времени.

Два колебания с одинаковыми амплитудами и частотами могут отличаться друг от друга фазами. Так как $ω=/$, то

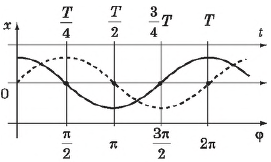
Отношение $/$ показывает, какая часть периода прошла от момента начала колебаний. Любому значению времени, выраженному в долях периода, соответствует значение фазы, выраженной в радианах. Сплошная кривая — это зависимость координаты от времени и одновременно от фазы колебаний (верхние и нижние значения на оси абсцисс соответственно) для точки, совершающей гармонические колебания по закону:

Здесь начальная фаза равна нулю $φ_0=0$. В начальный момент времени амплитуда максимальна. Это соответствует случаю колебаний тела, прикрепленного к пружине (или маятника), которое в начальный момент времени отвели от положения равновесия и отпустили. Описание колебаний, начинающихся из положения равновесия (например, при кратковременном толчке покоящегося шарика), удобнее вести с помощью функции синуса:

Как известно, $cosφ=sin(φ+/)$, поэтому колебания, описываемые уравнениями $x=x_cosω_t$ и $x=sinω_t$, отличаются друг от друга только фазами. Разность фаз, или сдвиг фаз, составляет $/$. Чтобы определить сдвиг фаз, нужно колеблющуюся величину выразить через одну и ту же тригонометрическую функцию — косинус или синус. Пунктирная кривая сдвинута относительно сплошной на $/$.

Сравнивая уравнения свободных колебаний, координаты, скорости и ускорения материальной точки, находим, что колебания скорости опережают по фазе на $/$, а колебания ускорения — на $π$ колебания смещения (координаты).

Затухающие колебания

Затухание колебаний — это уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебательной системой.

Свободные колебания всегда являются затухающими колебаниями.

Потери энергии колебаний в механических системах связаны с превращением ее в теплоту вследствие трения и сопротивления окружающей среды.

Так, механическая энергия колебаний маятника расходуется на преодоление сил трения и сопротивления воздуха, переходя при этом во внутреннюю энергию.

Амплитуда колебаний постепенно уменьшается, и через некоторое время колебания прекращаются. Такие колебания называются затухающими.

Чем больше силы сопротивления движению, тем быстрее прекращаются колебания. Например, в воде колебания прекращаются быстрее, чем в воздухе.

Упругие волны (механические волны)

Возмущения, распространяющиеся в пространстве, удаляясь от места их возникновения, называют волнами.

Упругие волны — это возмущения, распространяющиеся в твердой, жидкой и газообразной средах благодаря действию в них сил упругости.

Сами эти среды называют упругими. Возмущение упругой среды — это любое отклонение частиц этой среды от своего положения равновесия.

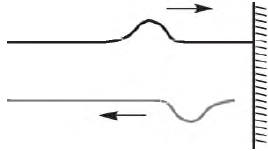
Возьмем, например, длинную веревку (или резиновую трубку) и прикрепим один из ее концов к стене. Туго натянув веревку, резким боковым движением руки создадим на ее незакрепленном конце кратковременное возмущение. Мы увидим, что это возмущение побежит вдоль веревки и, дойдя до стены, отразится назад.

Начальное возмущение среды, приводящее к появлению в ней волны, вызывается действием в ней какого-нибудь инородного тела, которое называют источником волны. Это может быть рука человека, ударившего по веревке, камешек, упавший в воду, и т. д.

Если действие источника носит кратковременный характер, то в среде возникает так называемая одиночная волна. Если же источник волны совершает длительное колебательное движение, то волны в среде начинают идти одна за другой. Подобную картину можно увидеть, поместив над ванной с водой вибрирующую пластину, имеющую наконечник, опущенный в воду.

Необходимым условием возникновения упругой волны является появление в момент возникновения возмущения сил упругости, препятствующих этому возмущению. Эти силы стремятся сблизить соседние частицы среды, если они расходятся, и отдалить их, когда они сближаются. Действуя на все более удаленные от источника частицы среды, силы упругости начинают выводить их из положения равновесия. Постепенно все частицы среды одна за другой вовлекаются в колебательное движение. Распространение этих колебаний и проявляется в виде волны.

В любой упругой среде одновременно существуют два вида движения: колебания частиц среды и распространение возмущения. Волна, в которой частицы среды колеблются вдоль направления ее распространения, называется продольной, а волна, в которой частицы среды колеблются поперек направления ее распространения, называется поперечной.

Продольная волна

Волна, в которой колебания происходят вдоль направления распространения волны, называется продольной.

В упругой продольной волне возмущения представляют собой сжатия и разрежения среды. Деформация сжатия сопровождается возникновением сил упругости в любой среде. Поэтому продольные волны могут распространяться во всех средах (и в жидких, и в твердых, и в газообразных).

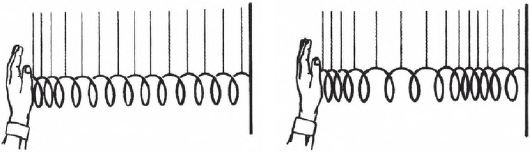
Пример распространения продольной упругой волны изображен на рисунке. По левому концу длинной пружины, подвешенной на нитях, ударяют рукой. От удара несколько витков сближаются, возникает сила упругости, под действием которой эти витки начинают расходиться. Продолжая движение по инерции, они будут продолжать расходиться, минуя положение равновесия и образуя в этом месте разрежение. При ритмичном воздействии витки на конце пружины будут то сближаться, то отходить друг от друга, т. е. колебаться возле своего положения равновесия. Эти колебания постепенно передадутся от витка к витку вдоль всей пружины. По пружине распространятся сгущения и разрежения витков, или упругая волна.

Поперечная волна

Волны, в которых колебания происходят перпендикулярно направлению их распространения, называются поперечными.

В поперечной упругой волне возмущения представляют собой смещения (сдвиги) одних слоев среды относительно других. Деформация сдвига приводит к появлению сил упругости только в твердых телах: сдвиг слоев в газах и жидкостях возникновением сил упругости не сопровождается. Поэтому поперечные волны могут распространяться только в твердых телах.

Плоская волна

Плоская волна — это волна, у которой направление распространения одинаково во всех точках пространства.

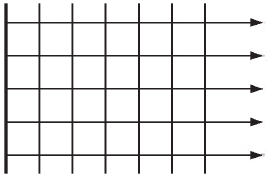
В такой волне амплитуда не меняется со временем (по мере удаления от источника). Получить такую волну можно, если большую пластину, находящуюся в сплошной однородной упругой среде, заставить колебаться перпендикулярно плоскости. Тогда все точки среды, примыкающей к пластине, будут колебаться с одинаковыми амплитудами и одинаковыми фазами. Распространяться эти колебания будут в виде волн в направлении нормали к пластине, причем все частицы среды, лежащие в плоскостях, параллельных пластине, будут колебаться с одинаковыми фазами.

Геометрическое место точек, в которых фаза колебаний имеет одно и то же значение, называется волновой поверхностью, или фронтом волны.

С этой точки зрения плоской волне можно дать и следующее определение.

Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу.

Линия, нормальная к волновой поверхности, называется лучом. Вдоль лучей происходит перенос энергии волны. Для плоских волн лучи — это параллельные прямые.

Уравнение плоской синусоидальной волны имеет вид:

где $s$ — смещение колеблющейся точки, $s_m$ — амплитуда колебаний, $ω$ — циклическая частота, $t$ — время, $х$ — текущая координата, $υ$ — скорость распространения колебаний или скорость волны, $φ_0$ — начальная фаза колебаний.

Сферическая волна

Сферической называется волна, волновые поверхности которой имеют вид концентрических сфер. Центр этих сфер называется центром волны.

Лучи в такой волне направлены вдоль радиусов, расходящихся от центра волны. На рисунке источником волны является пульсирующая сфера.

Амплитуда колебаний частиц в сферической волне обязательно убывает по мере удаления от источника. Энергия, излучаемая источником, равномерно распределяется по поверхности сферы, радиус которой непрерывно увеличивается по мере распространения волны. Уравнение сферической волны имеет вид:

В отличие от плоской волны, где $s_m=A$ — амплитуда волны постоянная величина, в сферической волне она убывает с расстоянием от центра волны.

Длина и скорость волны

Любая волна распространяется с некоторой скоростью. Под скоростью волны понимают скорость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около $5$ км/с.

Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.

Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.

Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:

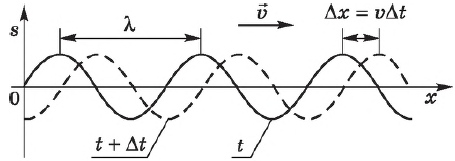
где $υ$ — скорость волны, $Т$ — период колебаний в волне, $λ$ (греческая буква лямбда) — длина волны.

Формула $λ=υT$ выражает связь длины волны с ее скоростью и периодом. Учитывая, что период колебаний в волне обратно пропорционален частоте $v$, т. е. $T=/$, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:

Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.

Длина волны — это пространственный период волны. На графике волны длина волны определяется как расстояние между двумя ближайшими точками гармонической бегущей волны, находящимися в одинаковой фазе колебаний. Рисунок — это как бы мгновенные фотографии волн в колеблющейся упругой среде в моменты времени $t$ и $t+∆t$. Ось $х$ совпадает с направлением распространения волны, на оси ординат отложены смещения $s$ колеблющихся частиц среды.

Частота колебаний в волне совпадает с частотой колебаний источника, т. к. колебания частиц в среде являются вынужденными и не зависят от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.

Интерференция и дифракция волн

Интерференция волн (от лат. inter — взаимно, между собой и ferio — ударяю, поражаю) — взаимное усиление или ослабление двух (или большего числа) волн при их наложении друг на друга при одновременном распространении в пространстве.

Обычно под интерференционным эффектом понимают тот факт, что результирующая интенсивность в одних точках пространства получается больше, в других — меньше суммарной интенсивности волн.

Интерференция волн — одно из основных свойств волн любой природы: упругих, электромагнитных, в том числе и световых, и др.

Интерференция механических волн

Сложение механических волн — их взаимное наложение — проще всего наблюдать на поверхности воды. Если возбудить две волны, бросив в воду два камня, то каждая из этих волн ведет себя так, как будто другой волны не существует. Аналогично ведут себя звуковые волны от разных независимых источников. В каждой точке среды колебания, вызванные волнами, просто складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.

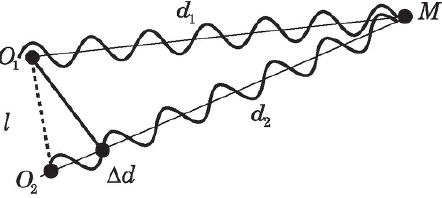
Если одновременно в двух точках $О_1$ и $O_2$ возбудить в воде две когерентные гармонические волны, то будут наблюдаться гребни и впадины на поверхности воды, не меняющиеся со временем, т. е. возникнет интерференция.

Условием возникновения максимума интенсивности в некоторой точке $М$, находящейся на расстояниях $d_1$ и $d_2$ от источников волн $О_1$ и $О_2$, расстояние между которыми $l 50—60$ мс. Тогда возникает многократное эхо. Некоторые из таких явлений приобрели мировую известность. Так, например, скалы, расположенные в форме круга возле Адерсбаха в Чехии, в определенном месте повторяют $7$ слогов, а в замке Вудсток в Англии эхо отчетливо повторяет $17$ слогов!

Слово «эхо» связано с именем горной нимфы Эхо, которая, согласно древнегреческой мифологии, безответно была влюблена в Нарцисса. От тоски по возлюбленному Эхо высохла и окаменела так, что от нее остался лишь голос, способный повторять окончания произнесенных в ее присутствии слов.

Почему не слышно эхо в небольшой квартире? Ведь и в ней звук должен отражаться от стен, потолка, пола. Дело в том, что время $t$, за которое звук проходит расстояние, скажем, $s=6м$, распространяясь со скоростью $υ=340$ м/с, равно:

А это значительно меньше времени ($0.06$ с), необходимого, чтобы услышать эхо.

Увеличение длительности звука, вызванное его отражениями от различных препятствий, называется реверберацией. Реверберация велика в пустых помещениях, где она приводит к гулкости. И наоборот, помещения с мягкой обивкой стен, драпировками, шторами, мягкой мебелью, коврами, а также наполненные людьми хорошо поглощают звук, и потому реверберация в них незначительна.

Скорость звука

Для распространения звука необходима упругая среда. В вакууме звуковые волны распространяться не могут, так как там нечему колебаться. В этом можно убедиться на простом опыте. Если поместить под стеклянный колокол электрический звонок, то по мере выкачивания из-под колокола воздуха звук от звонка будет становиться все слабее и слабее, пока не прекратится совсем.

Известно, что во время грозы мы видим вспышку молнии и лишь через некоторое время слышим раскаты грома. Это запаздывание возникает из-за того, что скорость звука в воздухе значительно меньше скорости света, идущего от молнии.

Скорость звука в воздухе впервые была измерена в 1636 г. французским ученым М. Мерсенном. При температуре $20°$С она равна $343$ м/с, т. е. $1235$ км/ч. Заметим, что именно до такого значения уменьшается на расстоянии $800$ м скорость пули, вылетевшей из автомата Калашникова. Начальная скорость пули $825$ м/с, что значительно превышает скорость звука в воздухе. Поэтому человек, услышавший звук выстрела или свист пули, может не беспокоиться: эта пуля его уже миновала. Пуля обгоняет звук выстрела и достигает своей жертвы до того, как приходит этот звук.

Скорость звука в газах зависит от температуры среды: с увеличением температуры воздуха она возрастает, а с уменьшением — убывает. При $0°$С скорость звука в воздухе составляет $332$ м/с.

В разных газах звук распространяется с разной скоростью. Чем больше масса молекул газа, тем меньше скорость звука в нем. Так, при температуре $0°$С скорость звука в водороде составляет $1284$ м/с, в гелии — $965$ м/с, а в кислороде — $316$ м/с.

Скорость звука в жидкостях, как правило, больше скорости звука в газах. Скорость звука в воде впервые была измеренав 1826 г. Ж. Колладоном и Я. Штурмом. Свои опыты они проводили на Женевском озере в Швейцарии. На одной лодке поджигали порох и одновременно ударяли в колокол, опущенный в воду. Звук этого колокола, опущенного в воду, улавливался на другой лодке, которая находилась на расстоянии $14$ км от первой. По интервалу времени между вспышкой светового сигнала и приходом звукового сигнала определили скорость звука в воде. При температуре $8°$С она оказалась равной $1440$ м/с.

Скорость звука в твердых телах больше, чем в жидкостях и газах. Если приложить ухо к рельсу, то после удара по другому концу рельса слышно два звука. Один из них достигает уха по рельсу, другой — по воздуху.

Хорошей проводимостью звука обладает земля. Поэтому в старые времена при осаде в крепостных стенах помещали «слухачей», которые по звуку, передаваемому землей, могли определить, ведет ли враг подкоп к стенам или нет. Прикладывая ухо к земле, также следили за приближением вражеской конницы.

Твердые тела хорошо проводят звук. Благодаря этому люди, потерявшие слух, иной раз способны танцевать под музыку, которая доходит до слуховых нервов не через воздух и наружное ухо, а через пол и кости.

Скорость звука можно определить, зная длину волны и частоту (или период) колебаний:

Инфразвук

Звуковые волны с частотой, меньшей $16$ Гц, называются инфразвуком.

Инфразвуковые волны человеческое ухо не воспринимает. Несмотря на это, они способны оказывать на человека определенное физиологическое воздействие. Объясняется это действие резонансом. Внутренние органы нашего тела имеют достаточно низкие собственные частоты: брюшная полость и грудная клетка — $5—8$ Гц, голова — $20—30$ Гц. Среднее значение резонансной частоты для всего тела составляет $6$ Гц. Имея частоты того же порядка, инфразвуковые волны заставляют наши органы вибрировать и при очень большой интенсивности способны привести к внутренним кровоизлияниям.

Специальные опыты показали, что облучение людей достаточно интенсивным инфразвуком может вызвать потерю чувства равновесия, тошноту, непроизвольное вращение глазных яблоки т. д. Например, на частоте $4—8$ Гц человек ощущает перемещение внутренних органов, а на частоте $12$ Гц — приступ морской болезни.

Рассказывают, что однажды американский физик Р. Вуд (прослывший среди коллег большим оригиналом и весельчаком) принес в театр специальный аппарат, излучающий инфразвуковые волны, и, включив его, направил на сцену. Никакого звука никто не услышал, однако с актрисой случилась истерика.

Резонансным влиянием на человеческий организм низкочастотных звуков объясняется и возбуждающее действие современной рок-музыки, насыщенной многократно усиленными низкими частотами барабанов, бас-гитар.

Инфразвук не воспринимается человеческим ухом, однако его способны слышать некоторые животные. Например, медузы уверенно воспринимают инфразвуковые волны с частотой $8—13$ Гц, возникающие при шторме в результате взаимодействия потоков воздуха с гребнями морских волн. Достигая медуз, эти волны заранее (за $15$ часов!) «предупреждают» о приближающемся шторме.

Источниками инфразвука могут служить грозовые разряды, выстрелы, извержения вулканов, работающие двигатели реактивных самолетов, ветер, обтекающий гребни морских волн, и т. д. Для инфразвука характерно малое поглощение в различных средах, вследствие чего он может распространяться на очень большие расстояния. Это позволяет определить места сильных взрывов, положение стреляющего орудия, осуществлять контроль за подземными ядерными взрывами, предсказывать цунами и т. д.

Ультразвук

Упругие волны с частотой выше $20$ кГц называются ультразвуком.

Ультразвук в животном мире. Ультразвук, как и инфразвук, не воспринимается человеческим ухом, однако его способны излучать и воспринимать некоторые животные. Так, например, дельфины благодаря этому уверенно ориентируются в мутной воде. Посылая и принимая возвратившиеся назад ультразвуковые импульсы, они способны на расстоянии $20—30$ м обнаружить даже маленькую дробинку, осторожно опущенную в воду. Ультразвук помогает и летучим мышам, которые плохо видят или вообще ничего не видят. Издавая с помощью своего слухового аппарата ультразвуковые волны (до $250$ раз в секунду), они способны ориентироваться в полете и успешно ловить добычу даже в темноте. Любопытно, что у некоторых насекомых в ответ на это выработалась особая защитная реакция: отдельные виды ночных бабочек и жуков тоже оказались способными воспринимать ультразвуки, издаваемые летучими мышами, и, услышав их, они тут же складывают крылья, падают вниз и замирают на земле.

Ультразвуковые сигналы используются и некоторыми китами. Эти сигналы позволяют им охотиться на кальмаров при полном отсутствии света.

Установлено также, что ультразвуковые волны с частотой более $25$ кГц вызывают болезненные ощущения у птиц. Это используется, например, для отпугивания чаек от водоемовс питьевой водой.

Использование ультразвука в технике. Ультразвук находит широкое применение в науке и технике, где его получают с помощью различных механических (например, сирена) и электромеханических устройств.

Источники ультразвука устанавливают на кораблях и подводных лодках. Посылая короткие импульсы ультразвуковых волн, можно уловить их отражения от дна или каких-либо других предметов. По времени запаздывания отраженной волны можно судить о расстоянии до препятствия. Использующиеся при этом эхолоты и гидролокаторы позволяют измерять глубину моря, решать различные навигационные задачи (плавание вблизи скал, рифов и т. д.), осуществлять рыбопромысловую разведку (обнаруживать косяки рыб), а также решать военные задачи (поиск подводных лодок противника, бесперископные торпедные атаки и др.).

В промышленности по отражению ультразвука от трещин в металлических отливках судят о дефектах в изделиях.

Ультразвуки дробят жидкие и твердые вещества, образуя различные эмульсии и суспензии.

С помощью ультразвука удается осуществить пайку алюминиевых изделий, что с помощью других методов сделать не удается (так как на поверхности алюминия всегда имеется плотный слой оксидной пленки). Наконечник ультразвукового паяльника не только нагревается, но и совершает колебанияс частотой около $20$ кГц, благодаря чему оксидная пленка разрушается.

Преобразование ультразвука в электрические колебания, а их затем в свет позволяет осуществить звуковидение. При помощи звуковидения можно видеть предметы в непрозрачной для света воде.

В медицине при помощи ультразвука осуществляют сварку сломанных костей, обнаруживают опухоли, осуществляют диагностические исследования в акушерстве и т. д. Биологическое действие ультразвука (приводящее к гибели микробов) позволяет использовать его для пастерилизации молока, стерилизации медицинских инструментов.

📹 Видео

Математический маятник или откуда формула периодаСкачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Колебания пружинного маятникаСкачать

Физика 9 класс. Уравнение механического движения пружинного маятникаСкачать

Колебательное движение. Свободные колебания | Физика 9 класс #23 | ИнфоурокСкачать

Дифференциальные уравнения для самых маленькихСкачать

Механические колебания. Математический маятник | Физика 11 класс #7 | ИнфоурокСкачать