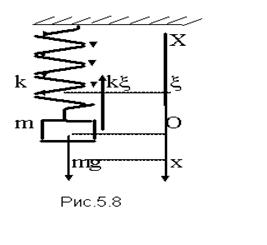
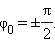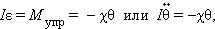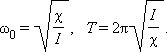Свободные колебания. Рассмотрим колебания груза массы m, висящего на пружине, жесткость которой. Направим ось координат Х вертикально вниз,
причем за начало отсчета примем точку О (рис.5.8), лежащую на одном уровне с центром масс m, когда груз неподвижен. При этом пружина растянута на величину x по сравнению с недеформированном состоянием. Величина упругой силы, действующей на массу m, равна kx. В положении равновесия
Если теперь сместить груз из положения равновесия, то он начнет совершать колебательное движение. Колебания, которые происходят в системе, выведенной из положения равновесия и затем предоставленной самой себе, называются свободными или собственными колебаниями,а частота, с которой происходят эти колебания, называется собственной частотой.Пусть в некоторый момент времени смещение груза равно х. Тогда второй закон Ньютона в проекции на ось Х может быть записан в следующем виде:
max = mg — k (x +x) или с учетом (5-13)
В свою очередь, уравнение (5-14) можно записать иначе, если представить ускорение тела через вторую производную смещения по времени ax = d 2 x/dt 2 и обозначить величину k/m = 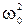
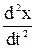
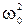
Уравнение (5-15) является дифференциальным уравнением второго порядка, однако его решение можно просто угадать простым перебором всех элементарных функций, из которых только функции синуса и косинуса удовлетворяют решению этого уравнения. Действительно, если
смещение x = A sin(w0t + j), (5-16)
то скорость тела 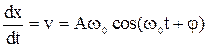
и ускорение тела 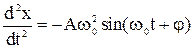
Сравнение (5-16) и (5-18) показывает, что действительно (5-16) является решением уравнения (5-15). Величины А и j остаются произвольными, для их определения необходимо использовать начальные условия, т.е. значения смещения и скорости тела в начальный момент времени. Например, если при t = 0 x (0)= 0, а v(0) = v0, то из (5-16 ) следует, что sinj = 0 и j = 0, a из (5-17) величина А = v0/w0. При этих условиях решением уравнения (5-15) служит функция х(t) = 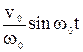
Затухающие колебания. В реальной жизни любой колебательный процесс постепенно затухает из-за наличия сил трения. Для колебаний груза на пружине существенную роль играет так называемое вязкое трение, сила которого при малых смещениях оказывается пропорциональной величине скорости тела:
Fтрен = — bv = — b 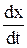
В этом случае второй закон Ньютона (уравнение движения) для груза, колеблющегося на пружине, приобретает такой вид:

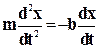
Вводя обозначения 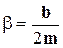
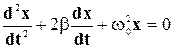
где по-прежнему 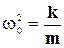
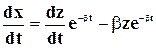
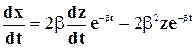
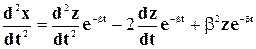
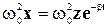
С учетом этого уравнение (5-21) может быть записано в таком виде:
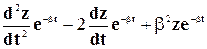
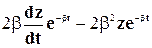
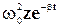
После сокращения на величину 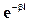
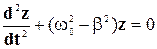
Сравнивая полученное уравнение с выражением (5-15), нетрудно заметить их почти полную идентичность; различие состоит лишь в том, что частота колебаний в (5-22) определяется из формулы 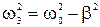
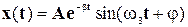
где как и ранее величины А и j определяются из начальных условий. В большинстве случаев b
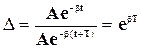
т.е. декремент затухания равен относительному уменьшению амплитуды за время, равное периоду колебания. Натуральный логарифм D называют логарифмическим декрементом затухания d, т.е. d = ln D = bТ.
Дата добавления: 2015-04-15 ; просмотров: 2767 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

1.1. Уравнение гармонических колебаний
В этом разделе мы покажем, что уравнения колебательного движения многих систем, в сущности, одинаковы, так что различные физические процессы могут быть описаны одними и теми же математическими формулами.
Пружинный маятник — это система, состоящая из шарика массой m, подвешенного на пружине длиной 
Рис. 1.2. К выводу уравнения движения для пружинного маятника
В положении равновесия (рис. 1.2) сила тяжести 

где 
Если теперь оттянуть шарик от положения равновесия на расстояние x, то полное удлинение пружины станет равным 
Знак минус означает, что сила стремится уменьшить отклонение от положения равновесия. Полученное выражение соответствует упругой силе слабо деформированной пружины.
Запишем теперь уравнение второго закона Ньютона:
Его можно также представить в виде:
Математический маятник
Математический маятник — это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.
Будем характеризовать отклонение маятника от положения равновесия углом 
Рис. 1.3. К выводу уравнения движения математического маятника
При отклонении маятника от положения равновесия на материальную точку массой m действуют сила тяжести 


Проецируя его на направления нормали и касательной к траектории (окружности радиуса 
Модуль скорости 




Тогда второе из написанных выше уравнений движения приобретает вид
При малых отклонениях маятника от вертикали, когда 
Физический маятник
Физический маятник — это протяженное колеблющееся тело, закрепленное на оси. Его размеры таковы, что его невозможно рассматривать как материальную точку.
Пример физического маятника приведен на рис. 1.4.
Рис. 1.4. К выводу уравнения движения физического маятника
При отклонении маятника от положения равновесия на угол 
где m – масса маятника, а l – расстояние 0C между точкой подвеса 0 и центром масс C маятника.
Рассматривая 




Ограничимся рассмотрением малых отклонений от положения равновесия:
В этом случае уравнение колебаний принимает вид:
В случае, когда физический маятник можно представить как материальную точку, колеблющуюся на нити длиной l, момент инерции равен
и мы приходим к уравнению (1.6) движения математического маятника.
Колебания поршня в сосуде с идеальным газом
Рассмотрим цилиндр с площадью поперечного сечения 




Рис. 1.5. Колебания поршня, закрывающего сосуд с идеальным газом
В состоянии равновесия давление в газе под поршнем складывается из атмосферного давления 


Переместим поршень на расстояние x вверх. Объем сосуда увеличится и станет равным
Соответственно уменьшится давление. В силу предположения об отсутствии теплообмена, новое давление в газе можно найти из уравнения адиабаты Пуассона
Здесь 
При малых колебаниях, когда изменение объема газа 

выражение (1.11) можно разложить в ряд Тейлора:
На поршень действуют три силы: сила атмосферного давления 



Используя (1.13), уравнение движения поршня
Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Дифференциальное уравнение гармонических колебаний
Таким образом, синусоидальное колебание физической величины s можно выразить, например, соотношением
Дифференцируя (3.4) по времени, получаем скорость изменения величины s
а повторное дифференцирование даст ускорение
Однако согласно (3.4) s = 5sin(co/ + фо) и есть сама функция, поэтому (3.6) можно представить в виде
Равенство (3.7) является дифференциальным уравнением гармонических колебаний. Его решением являются зависимости (3.1). Круговая частота называется частотой собственных колебаний системы.
Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Механические колебания
Простейшими механическими системами, совершающими колебательные движения, являются маятники.
Пружинный маятник. Пружинным маятником называется груз массой т, закрепленный на конце пружины (рис. 3.2). Груз может скользить (без трения) по горизонтальной плоскости. Оттянем груз из положения равновесия (точка О) на некоторое расстояние х. Тогда со стороны пружины на него будет действовать упругая сила F = —kx (см. (1.20)). Если груз отпустить, то под ее действием он начнет двигаться влево с ускорением а = d 2 x/c 2 . Согласно второму закону Ньютона
откуда
Сравнивая это выражение с (3.7), видим, что оно является дифференциальным уравнением гармонических колебаний пружинного маятника:
где со — круговая частота колебаний, со = -jk/т. Решением этого уравнения
будет зависимость х = Jfsin((o/‘ + сро), где X — амплитуда колебаний.
Физический маятник. Физическим маятником называется твердое тело, которое может колебаться около горизонтальной оси О, не проходящей через центр тяжести (рис. 3.3). В положении равновесия физический маятник располагается так, что центр тяжести тела С находится на одной вертикали 00 с точкой подвеса
О. Если маятник вывести из положения равновесия, отклонив его ось ОС от вертикали на небольшой угол а, на него будет действовать момент сил
где т — масса тела; mg — сила тяжести, приложенная к телу в центре тяжести С. Величина ОС = d = I sin а — плечо силы тяжести. Знак «—» в формуле (3.10) означает, что момент М действует на маятник в сторону уменьшения угла а.
Под действием момента М тело получит угловое ускорение в, связанное с моментом М зависимостью (2.14):
Если угол а мал, то sin a « а. Подставляя эти значения в (3.10), получаем

Сравнивая (3.11) c (3.8), замечаем, что при малых а физический маятник совершает гармонические колебания. Решением уравнения (3.11) будет
где а,„ — амплитуда колебаний; со — циклическая частота собственных колебаний физического маятника:

Математический маятник. Математическим маятником называется материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной / (рис. 3.4). Математический маятник является частным случаем физического, поэтому отклоненный от вертикали на угол а, он совершает гармонические колебания, описываемые зависимостью (3.12). Уравнение для циклической частоты этих колебаний можно получить, подставив в (3.13) выражение для момента инерции математического маятника I = ml 2 :
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Дифференциальное уравнение и его решение на примере грузика на пружине
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению (см. §2.1):
| . |
В этом соотношении – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:
| . |
Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .
Таким образом, груз некоторой массы , прикрепленный к пружине жесткости , второй конец которой закреплен неподвижно (рис. 2.2.1), составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором .
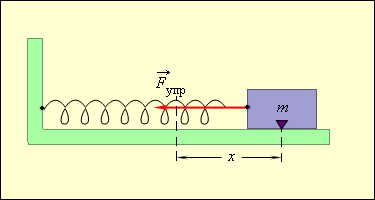 | ||||||||||||||||
| Рисунок 2.2.1. Круговая частота свободных колебаний груза на пружине находится из второго закона Ньютона:
откуда
Частота называется собственной частотой колебательной системы. Период гармонических колебаний груза на пружине равен
При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину , равную
и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты и периода колебаний справедливы и в этом случае. Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела и координатой : ускорение является второй производной координаты тела по времени :
Поэтому второй закон Ньютона для груза на пружине может быть записан в виде
или
где Все физические системы (не только механические), описываемые уравнением (*), способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида
Уравнение (*) называется уравнением свободных колебаний . Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний или период . Такие параметры колебательного процесса, как амплитуда m и начальная фаза , определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени. Если, например, груз был смещен из положения равновесия на расстояние и затем в момент времени отпущен без начальной скорости, то m = , . Если же грузу, находившемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость Таким образом, амплитуда m свободных колебаний и его начальная фаза определяются начальными условиями . Существует много разновидностей механических колебательных систем, в которых используются силы упругих деформаций. На рис. 2.2.2 показан угловой аналог линейного гармонического осциллятора, совершающий крутильные колебания. Горизонтально расположенный диск висит на упругой нити, закрепленной в его центре масс. При повороте диска на угол возникает момент сил упругой деформации кручения:
Это соотношение выражает закон Гука для деформации кручения. Величина аналогична жесткости пружины . Второй закон Ньютона для вращательного движения диска записывается в виде (см. §1.23)
где – момент инерции диска относительно оси, проходящий через центр масс, – угловое ускорение. По аналогии с грузом на пружине можно получить:
Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки. 🎥 ВидеоЗадача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать  Дифференциальные уравнения, 7 урок, Дифференциальные уравнения, допускающие понижение порядкаСкачать  Дифференциальные уравнения для самых маленькихСкачать  Дифференциальные уравнения. 11 класс.Скачать  НАСКОЛЬКО РАЗВИТО ТВОЕ ВНИМАНИЕ? Видео тест на зрение и концентрациюСкачать  Подготовка к экзамену. Динамика.Скачать  2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать  Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать  14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать  Как распознать талантливого математикаСкачать  11. Уравнения в полных дифференциалахСкачать  Дифференциальные уравнения 1. Вязкое торможениеСкачать  12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать  ЛОДУ 2 порядка c постоянными коэффициентамиСкачать  МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать  |












































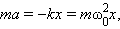
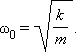
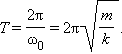
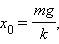
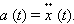
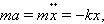
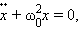
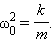
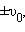 то
то