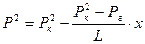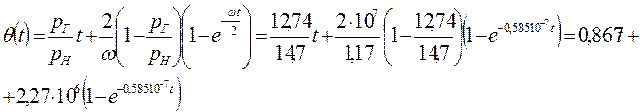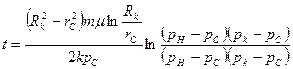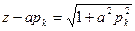Исследования показали, что хотя при установившейся фильтрации газа и происходит понижение температуры, оно относительно невелико даже при больших перепадах давления. Во многих случаях можно принимать для практических целей, что установившаяся фильтрация газа в пористых породах совершается в условиях изотермического изменения его состояния.
1. Дифференциальное уравнение установившейся фильтрации идеального газа.
Как было сказано ранее, для вывода дифференциального уравнения необходимо совместное решение уравнения неразрывности потока, уравнения движения и уравнения состояния.
Уравнение неразрывности потока:
(1)
(2)
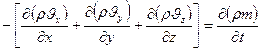
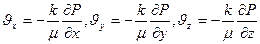
Уравнение состояния идеального газа:
(3)
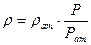
При установившейся фильтрации идеального газа
= 0 (4)
С учетом (2) – (4) уравнение (1) принимает вид:
= 0
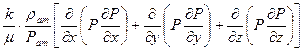
или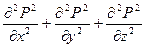 
= 0 (5)
Сравнивая дифференциальное уравнение установившейся фильтрации идеального газа (5) с дифференциальным уравнением установившейся фильтрации несжимаемой жидкости, можно сделать вывод о аналогии, т. е. решения уравнения (5) должны быть аналогичны решениям дифференциального уравнения установившейся фильтрации несжимаемой жидкости. Только вместо Р необходимо брать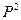 
.
2. Прямолинейно-параллельный поток идеального газа.
Дифференциальное уравнение (5) в этом случае будет иметь вид:
= 0 (6)
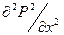
Примем граничные условия:
при x=0; 
при x=L (7)
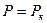
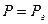
По аналогии с установившимся движением несжимаемой жидкости решение уравнения (6) при условиях (7) дает закон распределения давления в виде:
или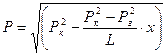 
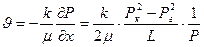
(8)
(9)
Дебит галереи, приведенный к атмосферному давлению
(10)
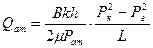
Средневзвешенное по объему пластовое давление
(11)
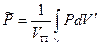
где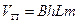 
, 
, 
.
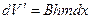
Тогда 
После интегрирования получим
(12)
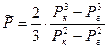
3. Плоскорадиальный фильтрационный поток идеального газа.
Дифференциальное уравнение (5) будет иметь вид:
= 0 (13)
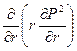
которое решается при следующих граничных условиях
при 
при 
(14)
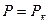
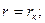
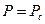
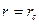
Решение уравнения (13) имеет вид:
(15)
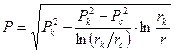
Уравнение (15) представляет собой закон распределения давления в пласте.
(16)
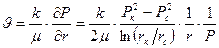
Дебит газовой скважины, приведенный к атмосферному давлению,
(17)
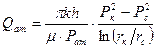
Средневзвешенное по объему пластовое давление определяется по (11) при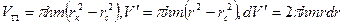 
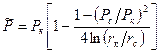
. После интегрирования (11) получим, пренебрегая величиной 
,
(18)
4. Плоскорадиальный фильтрационный поток реального газа по закону Дарси.
Если пластовое давление выше 10МПа и депрессия не слишком мала (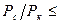 
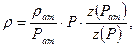
0,9), то уравнение состояния газа значительно отличается от уравнения состояния идеального газа и плотность газа определяется по формуле:
(19)
где z – коэффициент сверхсжимаемости газа. Кроме того, для высоких пластовых давлений нужно учитывать зависимость вязкости от давления
(20)
или при малых изменениях давления
(21)
где µ0 — вязкость при фиксированном давлении;
αµ — коэффициент, определяемый экспериментально и зависящий от состава газа.
Проницаемость пласта принимается постоянной.
Дебит газовой скважины, приведенный к атмосферному давлению,
(22)
Имеется несколько способов вычисления интеграла в формуле (22), наиболее употребляем из которых следующий: по графикам зависимостей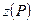 
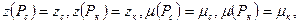
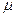
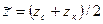
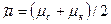
и 
определяются значения 
переменные 
и z под знаком интеграла заменяются постоянными, равными 
, 
.
Тогда интеграл в формуле (22) вычисляется и (22) принимает следующий вид:
.
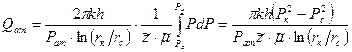
Основная литература: 2 125
Дополнительная литература: 4 74
Контрольные вопросы:
1. Какой газ называется идеальным?
2. Уравнения состояния идеального и реального газов.
3. Дифференциальное уравнение установившейся фильтрации идеального газа.
4. Закон распределения давления при фильтрации идеального газа.
5. Дебит газовой скважины.
6. Средневзвешенное по объему пластовое давление.
7. Коэффициент сверхжимаемости.
8. Зависимость вязкости реального газа от давления.
9. Дебит газовой скважины при фильтрации реального газа.
Дата добавления: 2016-03-10 ; просмотров: 1687 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать
XIII. НЕУСТАНОВИВШАЯСЯ ФИЛЬТРАЦИЯ ГАЗА
Дифференциальное уравнение неустановившейся изотермической фильтрации идеального газа по закону Дарси имеет вид
(XIII.1)
(XIII.2)
Это уравнение является нелинейным уравнением параболического типа, оно отличается от дифференциального уравнения упругого режима тем, что искомой функцией является не давление р, а квадрат давления р 2 , а вместо постоянного коэффициента пьезопроводности х в уравнение входит переменная величина kp/mx.
Точные решения нелинейного уравнения (XIII.2) получены только для некоторых частных задач. Как правило, это уравнение интегрируется приближенными методами.
Наиболее простым приближенным методом является метод линеаризации, предложенный И. А. Чарным, в котором переменное значение коэффициента kp/mµ заменяется усредненным значением kpср/mµ, где
здесь рmax и рmin — максимальное и минимальное давления в залежи за расчетный период, или
При такой замене уравнение (XIII.2) приводится к линейному дифференциальному уравнению теплопроводности. Это дает возможность нестационарное движение газа рассчитывать жак движение упругой жидкости по формулам упругого режима фильтрации.
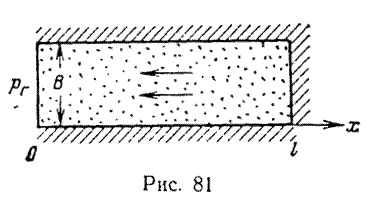
Л. С. Лейбензоном было лолучено решение задачи об истечении газа из полосообразного замкнутого пласта при условии постоянного давления на галерее (рис. 81). Задача сводится к интегрированию дифференциального уравнения
(XIII.3)
при начальном и граничных условиях:
при t=0
при x=0
при x=l (XIII.4)
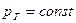
— условие на непроницаемой границе газового пласта.
Задача решалась методом последовательных приближений.
В первом приближении коэффициент, входящий в правую часть (XIII.3), считается постоянным и равным 
.
При этом (XIII.3) обращается в уравнение теплопроводности, интеграл которого при условиях (XII 1.4) имеет вид
(XIII.5)
Во втором приближении принимается, что переменное давление p, входящее в коэффициент kp/mµ, зависит только от времени t и выражается формулой
(XIII.6)
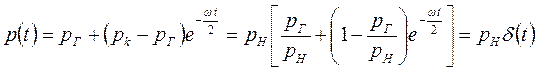
далее, введя новую переменную
(XIII.7)
приведем (XIII.3) к уравнению теплопроводности
(XIII.8)
решение которого при условиях (XIII.4) дается уравнением (XIII.5), в котором переменная t должна быть заменена на θ:
(XIII.9)
Объемный дебит галереи, приведенный к атмосферному давлению, можно записать в виде
(XIII.10)
Многие задачи неустановившейся фильтрации газа решаются «приближенно по методу последовательной смены стационарных состояний с привлечением уравнения материального баланса газа.
Если газовая залежь замкнута, то отобранное за время dt количество газа по объему, приведенному к атмосферному давлению и пластовой температуре, равное 
, равно изменению запасов газа в пласте за тот же промежуток времени.
Если объем порового пространства Ω постоянный, газ идеальный, а фильтрация изотермическая, то изменение запасов можно представить в виде 
, где dp — изменение средневзвешенного по объему давления в газовой залежи за промежуток dt. Уравнение
(XIII.11)
называется дифференциальным уравнением истощения газовой залежи.
При неустановившейся плоскорадиальной фильтрации газа средневзвешенное давление 
мало отличается от контурного, поэтому, заменяя на pk записывают уравнение истощения газовой залежи в виде
(XIII.12)
Уравнение (XIII. 12) в сочетании с методом последовательной смены стационарных состояний позволяет определять распределение давления по пласту, изменение давления с течением времени в любой точке пласта, изменение во времени дебитов таза при эксплуатации залежи с различными условиями на забое. Такими простейшими условиями являются следующие: ..a) Qaт = const; б) pc = const; в) 
, где c = 2nrchwmax, a wmax — максимально допустимая скорость фильтрации газа, исключающая возможность выноса песка и образования песчаных пробок.
Определить падение давления рк на внешней границе полосообразной газовой залежи длиной l = 7500 м, шириной В = 800 м, мощностью h= 10 м (см. рис. 81), если коэффициент пористости пласта m = 20%, коэффициент проницаемости k = 0,5 Д, коэффициент вязкости µ = 0,014 мПа•с, начальное пластовое давление рн = 14,7МПа (150 кгс/см 2 ). Давление на выходе газа в галерею постоянно и равно рг= 12,74 МПа (130 кгс/см 2 ).
Найти также приведенный к атмосферному давлению и пластовой температуре расход газа Qат и распределение давления по длине пласта через t = 30 сут после начала отбора газа из галереи.
Решение.Для определения падения давления во времени на границе пласта рк(t) и распределения давления по длине пласта р(х) в момент t = 30 сут используем решение Л. С. Лейбеизона по методу последовательных приближений (XIII.9).
Прежде всего подсчитаем значение параметра
и значения переменной Q(t) в разные моменты
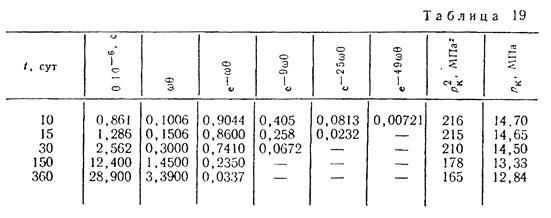
а результаты поместим в табл. 19.
По формуле Л. С. Лейбензона на границе пласта (при x=l) имеем
Значения величин, входящих в эту формулу, приведены в табл. 19.
На рис. 82 представлен график зависимости рк(t).
Закон распределения давления по пласту через 30 сут = 2,59•10 6 с после начала отбора:
Результаты расчетов даны в табл. 20. На рис. 83 показана кривая изменения давления по пласту.
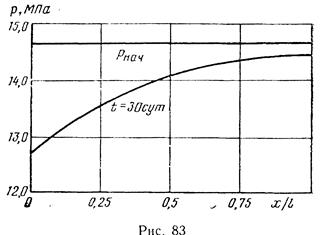
Расход газа, приведенный к атмосферному давлению и пластовой температуре, найдем по (XIII.10).
Газовая скважина расположена в центре кругового замкнутого пласта радиусом Rк=1000 м, мощностью h = 8 м и эксллуатируется при постоянном давлении на забое pc = 6,86 МПа (70 кгс/см 2 ). .Начальное давление в газовой залежи рн = 11,76 МПа (120 кгс/см 2 ), коэффициент проницаемости пласта k = 800 мД, коэффициент пористости пласта m=18%, динамический коэффициент вязкости газа µ = 0,013 мПа•с, радиус скважины rс= 10 см.
Найти изменение во времени давления на внешней границе залежи pk(t) и приведенного объемного дебита скважины.
Решение.Полагая, что средневзвешенное пластовое давление газа равно давлению на внешнем контуре рк, решим задачу методом последовательной смены стационарных состояний. За время dt при изотермическом процессе из залежи отбирается количество газа (по объему, приведенному к атмосферному давлению)
(XIII.13)
(XIII.14)
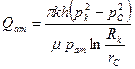
и подставляя эти выражения в уравнение материального баланса (XIII.13), получим
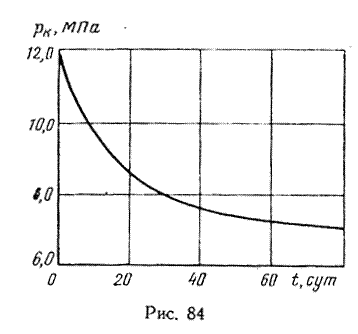
Подставляя исходные данные подсчитаем для различных рк значения t:
Результаты подсчетов представлены на рис. 84 и ниже.
pk, МПа …………..11,76 10,78 9,8 8,82 7,84 6,96
t, сут ………………0 3,77 8,88 16,5 30,5 80,5
Qат ,м 3 /cут ……….13,4·10 6 10,1·10 6 7,2·10 6 4,51·10 6 2,11·10 6 1,99·10 5
Подставляя найденные значения рк в (XIII.14), найдем изменение Qат во времени
Cоответствующие значения дебатов даны на рис. 85.
Определить время истощения газовой залежи и изменение во времени давления на внешней границе и на забое скважины, считая, что скважина дренирует круговую зону радиуса Rк = = 500 м и эксплуатируется с постоянным приведенным дебитом Qaт = 500 000 м 3 /сут. Начальное пластовое давление рн = 9,8 МПа (100 кгс/см 2 ), конечное давление на забое газовой скважины (Рс)кон = 0,101 МПа (1,033 кгс/см 2 ), мощность пласта h=12 м, радиус скважины rс=10 см, коэффициент проницаемости пласта k = 500 мД, коэффициент пористости m==20%, динамический коэффициент вязкости газа µ = 0,015 мПа·с.
Решение. Из уравнения материального баланса, в котором средневзвешенное пластовое давление заменено контурным, имеем
(XIII.15)
Интегрируя (XIII. 15) по рк в пределах от рн до рк и по t ют 0 до t получим
(XIII.16)
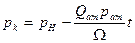
Из формулы дебита
найдем давление на забое скважины
(XIII.17)
По значению забойного давления в конце разработки рс.кон .найдем конечное значение давления на внешней границе рк.кон.
Подставляя полученное значение рк.кон в (XIII.16), найдем время истощения газовой залежи:
Изменение во времени рк и рс определяется из (XIII.16) и (ХШ.17).
Результаты подсчетов приведены на рис. 86 и ниже.
t, сут. О 50 100 150 200 291
рк, кгс/см 2 . 100 86,3 72,6 58,9 45,2 20,2
рс, кгс/см 2 . 97,9 83,9 69,7 55,3 40,5 1,033
Определить изменение во времени дебита газовой скважины, давления на внешней непроницаемой границе рк(t) и давления на забое скважины рс(t) эксплуатирующейся при поддержании постоянной скорости движения газа в призабойной зоне пласта. Начальное пластовое давление рн =9,8 МПа (100 кгс/см 2 ), радиус контура зоны дренирования Rk = 750 м, мощность пласта h=10 м, коэффициент проницаемости пласта k = 0,3 Д, коэффициент пористости пласта m = 20%, динамический коэффициент вязкости газа в пластовых условиях µ = 0,012 сП, радиус скважины rс = 0,1 м. Коэффициент с, который соответствует максимально допустимой скорости фильтрации в призабойной зоне, определяемый практически, равен 
. Принять атмосферное давление рат = 0,098 МПа (1 кгс/см 2 ).
Решение.Если газ отбирается при поддержании максимально допустимой скорости фильтрации wmax у забоя скважины, то приведенный дебит
(XIII.18)
(XIII.19)
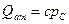
С другой стороны,
(XIII.20)
Приравнивая соотношения (XIII.19) и (XIII.20), найдем
Обозначая 
, запишем
(XIII.21)
Подставляя (XIII.21) в (XIII.19), найдем зависимость дебита Qат от pk
Из уравнения материального баланса, заменяя среднее пластовое давление контурным, найдем
(XIII.22)
Вводя новую переменную
и интегрируя дифференциальное уравнение (XI 11.22), получим
(XIII.23)
Подсчитаем объем норового пространства
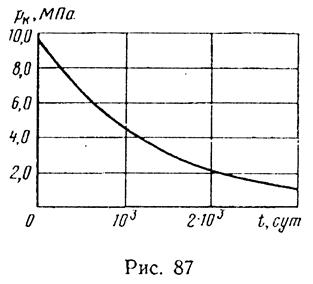
Подставляя численные значения параметров а, с, рат и рн в соотношение (XIII.23), задаваясь различными значениями рк, определим значения t. Соответствующие значения pc(t) и Qат<t) найдем из выражений (XIII.19) и (XIII.21). Результаты вычислений представлены на рис. 87, 88 и ниже.
t,сут ………………0 226 462 776 1196 1825 3130 4250 6100
pk , МПа…………9,8 8,33 6,86 5,39 3,92 2,45 0,980 0,490 0,210
pc ,МПа…………9,62 8,15 6,68 5,22 3,74 2,28 0,822 0,345 0,098
Qат ·10 -5 ,м 3 /сут..2,66 2,25 1,85 1,445 1,035 0,632 0,227 0,0955 0,0271
Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать
Сравнительный анализ прямолинейно-параллельного и плоскорадиального фильтрационных потоков идеального газа
Дифференциальные уравнения фильтрации газа
По линейному закону
Уравнение неразрывности потока сжимаемой жидкости в деформируемой пористой среде имеет вид:
. (7.1)
Уравнения движения в горизонтальном фильтрационном потоке записываются в виде:
 |
,
,
. (7.2)
Введем функцию P следующим образом. Примем, что ее дифференциал равен:
,
 |
— функция Л.С.Лейбензона. (7.3)
От дифференциала функции Л.С.Лейбензона, перейдем к частным производным:
 |
;
;
. (7.4)
Запишем уравнения движения для массовых скоростей фильтрации с учетом соотношений (7.4):
 |
;
;
.
Тогда уравнение неразрывности (7.1) можно записать в виде:
(7.6)
. (7.6’)
В случае установившейся фильтрации правая часть уравнений (7.6) обращается в 0, в результате чего можно записать:
(7.7)
или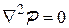 
.
Следовательно, функция Л.С.Лейбензона удовлетворяет уравнению Лапласа.
Аналогия между фильтрацией жидкости и идеального газа
Введение функции Л.С.Лейбензона в дифференциальные уравнения теории фильтрации позволяет установить аналогию между установившейся фильтрацией сжимаемого флюида (газа) и установившейся фильтрацией несжимаемой жидкости.
В наиболее простом случае можно считать K=const. При малых пластовых давлениях и небольших депрессиях можно также пренебречь зависимостью вязкости m от давления. Такое допущение справедливо для идеальных сред, в которых отсутствует внутреннее трение, обусловленное процессами внутреннего молекулярного обмена.
Тогда функцию Л.С.Лейбензона можно представить в виде:
,
при этом 
.
Сравним две записи закона Дарси в дифференциальной форме – для установившейся фильтрации несжимаемой жидкости и для установившейся фильтрации газа.
| Жидкость | Газ |
 где Q=const – объемный расход жидкости; f(S) – площадь поперечного сечения струи |  где Qm=rQ=const – массовый расход газа |
Данные уравнения однотипны, следовательно, все формулы, полученные для установившейся фильтрации жидкости, можно применять и для установившейся фильрации газа, используя аналогию следующих показателей:
| Несжимаемая жидкость | Газ | |
| объемный расход Q | — | массовый расход Qm |
| давление Р | — | функция Л.С.Лейбензона P |
| объемная скорость фильтрации V | — | массовая скорость фильтра-ции rV |
Сравнительный анализ прямолинейно-параллельного и плоскорадиального фильтрационных потоков идеального газа
Исследованиями Б.Б.Лапука было установлено, что фильтрацию газа в реальных пластах можно рассматривать как изотермический процесс, для которого справедлив закон Бойля-Мариотта. При T=const
,
где m – масса газа.
— уравнение состояния идеального газа.
С учетом уравнения состояния идеального газа выражение функции Л.С.Лейбензона приобретает вид:
.
| Характерис-тика | Прямолинейно-параллельный поток | Плоскорадиальный поток |
| Распределение давления | 1.  2.  | 1.  2.  |
| Градиент давле-ния | 1.  2.  | 1.  2.  |
| Скорость фильтрации | 1.  2.  | 1.  2.  |
| Дебит газа, при-веденнй к атмо-сферному дав-лению |  |  |
| Средневзвешен-ное пластовое давление |  |  |
Анализируя соотншения, можно отметить следующее.
В прямолинейно-параллельном потоке:
а) давление по длине пласта изменяется по параболическому закону, зависимость Р 2 (x) — линейная;
б) объемный расход газа, приведенный к атмосферному давлению, постоянный по длине пласта;
в) скорость фильтрации и градиент давления возрастают при приближении к галерее. Физически возрастание скорости фильтрации вдоль газового потока происходит за счет расширения газа при снижении давления.
 |
В плоскорадиальном потоке:
а) распределение давления подчинено логарифмическому и параболическому законам, поэтому в газовом потоке, в отличие от потока жидкости, имеет место резкое падение давления вблизи скважины и весьма малое – вдали от нее. Площадь и объем пласта с пониженным давлением вблизи скважины значительно меньше объема газового пласта в целом. Поэтому в газонасыщенном пласте давление повсюду считается одинаковым, приблизительно равным давлению на контуре питания;
б) градиент давления и скорость фильтрации вблизи забоя газовой скважины резко возрастают как за счет уменьшения r, так и за счет падения давления Р.
Индикаторная диаграмма при фильтрации газа строится в координатах 
и в установившемся плоскорадиальном потоке имеет прямолинейный характер.
💥 Видео
Уравнение состояния идеального газа. 10 класс.Скачать
Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать
Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать
Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать
Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать
Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать
Уравнение состояния идеального газаСкачать
5. Однородные дифференциальные уравнения. Часть 2.Скачать
Газовые законы. Изопроцессы | Физика 10 класс #34 | ИнфоурокСкачать
Математика это не ИсламСкачать
Уравнение идеального газа: PV = nRT | Газы.Молекулярно-кинетическая теория | Химия (видео 1)Скачать
идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать
Решение задач на основное уравнение МКТ идеального газа | Физика 10 класс #29 | ИнфоурокСкачать
