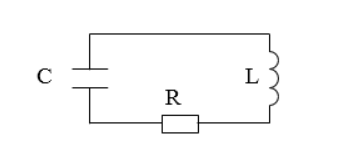
Дифференциальное уравнение для затухающих электромагнитных колебаний и его решение (8 видео)

Затухающие колебания в контуре и их уравнение

Существуют колебания в системе без источника энергии, называемые затухающими. Рассмотрим реальный контур с сопротивлением не равным нулю. Для примера используют контур с включенным сопротивлением R , с емкостью конденсатора C , с катушкой индуктивности L , изображенный на рисунке 1 . Колебания, происходящие в нем, — затухающие.

Именно наличие сопротивления становится главной причиной их затухания. Данный процесс возможен посредствам потерь энергии на выделение джоулева тепла. Аналог сопротивления в механике – действие сил трения.

Содержание

Характеристики затухающих колебаний
Уравнения затухающих колебаний
Дифференциальное уравнение свободных затухающих колебаний (механических и электромагнитных) и его решение. Автоколебания
Дифференциальное уравнение затухающих колебаний в электрическом контуре
🔥 Видео

Видео:Затухающие колебания Лекция 11-1Скачать

Характеристики затухающих колебаний

Затухающие колебания характеризуют коэффициентом затухания β . Применив второй закон Ньютона, получим:

m a = — k x — y v , d 2 x d t 2 + r m d x d t + k m x = 0 , ω 0 2 = k m , β = r 2 m .

Из записи видно, что β действительно является характеристикой контура. Реже вместо β применяют декремент затухания δ ,

Значение a ( t ) является амплитудой заряда, силы тока и так далее, δ равняется количеству колебаний, а N e — период времени уменьшения амплитуды в e раз.

Для R L C контура применима формула с ω частотой.

При небольшой δ ≪ 1 говорят, что β ≪ ω 0 ω 0 = 1 L C — собственная частота, отсюда ω ≈ ω 0 .

При рассмотрении затухающих колебаний последовательного контура колебательный контур характеризуется добротностью Q :

Q = 1 R L C = ω 0 L R , где R , L и C — сопротивление, индуктивность, емкость, а ω 0 — частота резонанса. Выражение L C называют характеристическим или волновым сопротивлением. Для параллельного контура формула примет вид:

Q = R L C = R ω 0 L .

R является входным сопротивлением параллельного контура.

Эквивалентное определение добротности применяется при слабых затуханиях. Его выражают через отношение энергий:

Q = ω 0 W P d = 2 π f 0 W P d , называемое общей формулой.

Видео:Урок 355. Затухающие электромагнитные колебания.Скачать

Уравнения затухающих колебаний

Рассмотрим рисунок 1 . Изменение заряда q на конденсаторе в таком контуре описывается дифференциальным уравнением:

q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .

Если t = 0 , то заряд конденсатора становится равным q 0 , и ток в цепи отсутствует.

Если R > 2 L C изменения заряда не относят к колебаниям, разряд называют апериодическим.

Значение сопротивления, при котором колебания превращаются в апериодический разряд конденсатора, критическое R k .

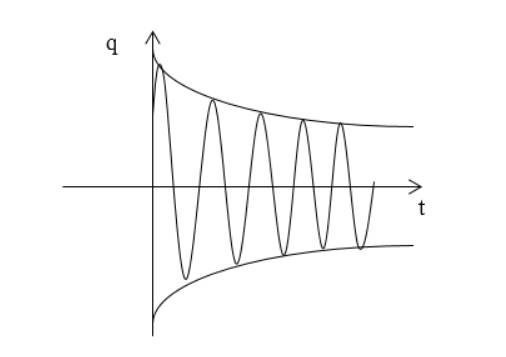
Функция изображается аналогично рисунку 2 .

Записать закон убывания энергии, запасенной в контуре W ( t ) при W ( t = 0 ) = W 0 с затухающими колебаниями. Обозначить коэффициент затухания в контуре β , а собственную частоту — ω 0 .

Решение

Отправная точка решения – это применение формулы изменения заряда на конденсаторе в R L C — контуре:

q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .

Предположим, что при t = 0 , a ‘ 0 = 0 . Тогда применим выражение

Для нахождения I ( t ) :

I ( t ) = — ω 0 q 0 e ( — 2 β t ) sin ( ω t + α ) , где t g α = β ω .

Очевидно, что электрическая энергия W q запишется как:

W q = q 2 2 C = q 0 2 2 C e ( — 2 β t ) cos 2 ( ω t ) = W 0 e ( — 2 β t ) cos 2 ( ω t ) .

Тогда значение магнитной энергии контура W m равняется:

W m = L 2 ω 0 2 q 0 2 e ( — 2 β t ) sin 2 ω t + a = W 0 e — 2 β t sin 2 ω t + a .

Запись полной энергии будет иметь вид:

W = W q + W m = W 0 e ( — 2 β t ) ( cos 2 ( ω t ) + sin 2 ( ω t + a ) ) = = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + α ) .

Где sin α = β ω 0 .

Ответ: W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) .

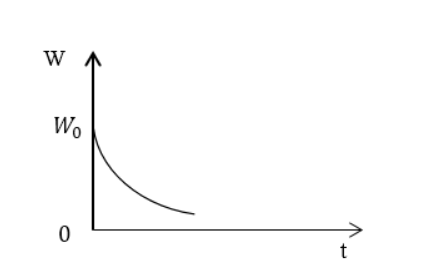
Применив результат предыдущего примера, записать выражение для энергии, запасенной в контуре W ( t ) , при медленно затухающих колебаниях. Начертить график убывания энергии.

Решение

Если колебания в контуре затухают медленно, то:

Очевидно, выражение энергии, запасенной в контуре, вычислим из

W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) , предварительно преобразовав до W ( t ) = W 0 e ( — 2 β t ) .

Такое упрощение возможно по причине выполнения условия β ω 0 ≪ 1 , sin ( 2 ω t + a ) ≤ 1 , что означает β ω 0 sin ( 2 ω t + a ) ≪ 1 .

Ответ: W ( t ) = W 0 e ( — 2 β t ) . Энергия в контуре убывает по экспоненте.

Видео:70. Затухающие колебанияСкачать

Дифференциальное уравнение свободных затухающих колебаний (механических и электромагнитных) и его решение. Автоколебания

Рассмотрим свободные затухающие колебания— колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах,

а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах.

Закон затухающих колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы— идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяются. Линейными системами являются, например, пружинный маятник при малых растяжениях пружины (когда справедлив закон Гука), колебательный контур, индуктивность, емкость и сопротивление которого не зависят ни от тока в контуре, ни от напряжения. Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями, что позволяет подходить к изучению колебаний различной физической природы с единой точки зрения, а также проводить их моделирование, в том числе и на ЭВМ.

Дифференциальное уравнение свободных затухающих колебанийлинейной системы задается в виде

где s — колеблющаяся величина, описывающая тот или иной физический процесс, d=const — коэффициент затухания,w₀ — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при d=0 (при отсутствии потерь энергии) называется собственной частотойколебательной системы.

Решение уравнения (146.1) рассмотрим в виде

где u=u(t). После нахождения первой и второй производных выражения (146.2) и подстановки их в (146.1) получим

Решение уравнения (146.3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положителен:

w 2 =w 2 ₀-d 2 (146.4)

(если (w 2 -d 2 )>0, то такое обозначение мы вправе сделать). Тогда получим уравнение типа (142.1)

решением которого является функция и=А₀cos(wt+j)

Таким образом, решение уравнения (146.1) в случае малых затуханий (d 2 2 ₀)

— амплитуда затухающих колебаний,а

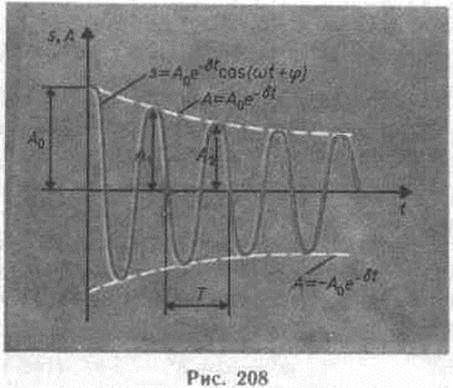
a₀— начальная амплитуда. Зависимость (146.5) показана на рис.208 сплошной линией, а зависимость (146.6) — штриховыми линиями. Промежуток времени t=1/d, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.

Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины (рис. 208). Тогда период затухающих колебаний с учетом формулы

Если A(t) и A(t+T)— амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение

называется декрементом затухания, а его

— логарифмическим декрементом затухания;N_e — число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина.

Для характеристики колебательной системы пользуются понятием добротностиQ, которая при малых значениях логарифмического декремента равна

(так как затухание невелико (d 2 2 ₀), то Т принято равным Т₀).

Из формулы (146.8) следует, что добротность пропорциональна числу колебаний N_e, совершаемых системой за время релаксации.

Применим выводы, полученные для свободных затухающих колебаний линейных систем, для колебаний различной физической природы — механических (в качестве примера рассмотрим пружинный маятник) и электромагнитных (в качестве примера рассмотрим электрический колебательный контур).

1. Свободные затухающие колебания пружинного маятника.Для пружинного маятника (см. § 142) массой т, совершающего малые колебания под действием упругой силы F=-kx, сила трения пропорциональна скорости, т. е.

где r — коэффициент сопротивления;знак минус указывает на противоположные направления силы трения и скорости.

При данных условиях закон движения маятника будет иметь вид

Используя формулу w₀=Ök/m (см. (142.2)) и принимая, что коэффициент затухания

получим идентичное уравнению (146.1) дифференциальное уравнение затухающих колебаний, маятника:

Из выражений (146.1) и (146.5) вытекает, что маятник колеблется по закону

х=A₀е — d t cos(wt+j) с частотой w=Ö(w 2 ₀-r2/4m 2 ) (см. (146.4)).

Добротность пружинного маятника,

согласно (146.8) и (146.10), Q=1/rÖkm.

Видео:71. Вынужденные колебанияСкачать

Дифференциальное уравнение затухающих колебаний в электрическом контуре

В электрических цепях колебания затухают из-за наличия омических сопротивлений в элементах цепи. Для анализа затухающих электрических колебаний рассмотрим эквивалентную схему контура (рис. 19).

Рис. 19. Эквивалентная схема электрического колебательного контура

Электрический ток I в контуре существует благодаря кулоновским силам заряженного конденсатора С и сторонним силам, возникающим в катушке индуктивности L. В некоторый момент времени конденсатор имеет заряд q , а напряжение между его пластинами равно U. При разряде конденсатора в катушке возникает э.д.с. самоиндукции e_L, пропорциональная скорости изменения тока:

Согласно закону Ома ток в цепи:

Преобразуем уравнение (3.4) к уравнению одной переменной, а именно, — напряжения U на обкладках конденсатора.

Ток в цепи равен убыли заряда q на конденсаторе:

Заряд конденсатора равен:

Подставив формулы (3.7), (3.8) в формулу (3.4), получим

Данное дифференциальное уравнение описывает затухающие колебания напряжения на обкладках конденсатора в электрическом контуре. Решение дифференциального уравнения (3.9) имеет вид

где (3 — коэффициент затухания

со — циклическая частота затухающих колебаний

где ю₀ — частота колебаний в отсутствии затуханий:

Период затухающих колебаний Т равен

При значении коэффициента затухания (3 = о>₀ возникает апериодический режим разряда конденсатора (режим критического затухания). Из формул (3.12-3.14) следует, что колебания возможны лишь при условии

то есть, если

Если R > , то частота и период становятся мнимыми, колебания

не возникают, разряд конденсатора становится апериодическим. Сопротивление контура, равное

[Г

называется критическим сопротивлением. Величина, равная J—,

называется волновым сопротивлением контура.

По аналогии с механическими затухающими колебаниями введем понятие декремента затухания. Декрементом затухания называется отношение двух последующих (разделенных интервалом временем равным периоду) амплитуд колебаний:

Декремент затухания D характеризует быстроту затухания колебаний и показывает, во сколько раз уменьшается амплитуда колебаний за время, равное одному периоду. Натуральный логарифм отношения (3.18) называется логарифмическим декрементом затухания:

Логарифмический декремент X затухания колебаний в электрическом контуре будет иметь следующее выражение:

Амплитуда колебаний в контуре убывает по экспоненциальному закону:

При t = амплитуда затухающих колебаний уменьшается в

2,72 раза, (т.е., в е раз). Это время обозначается т и называется временем релаксации колебательной системы. Время релаксации колебательной системы любой природы — это время, за которое амплитуда колебаний уменьшается в е = 2,72 раза.

Из формул (ЗЛ1), (3Л 8) -(3.20) следует

Кроме коэффициента затухания, декремента, логарифмического декремента и времени релаксации для характеристики затухающих колебаний используется понятие добротности. Добротность Q электрического контура (как и любой колебательной системы) пропорциональна отношению полной энергии колебаний W(t) к потерям энергии AW за один период Т: