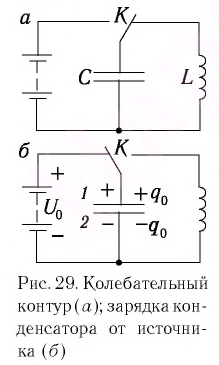
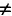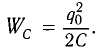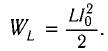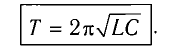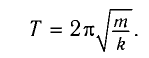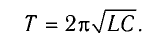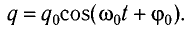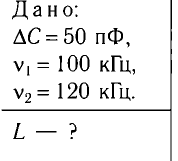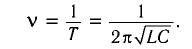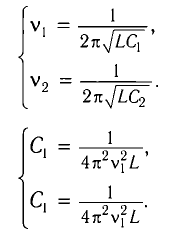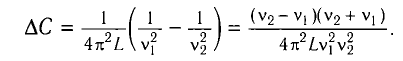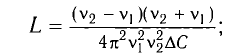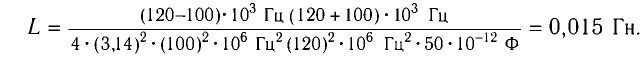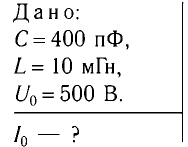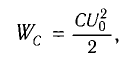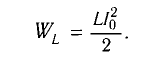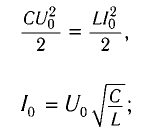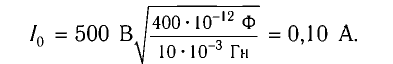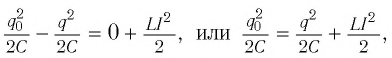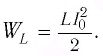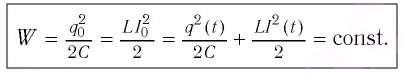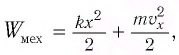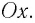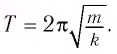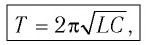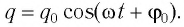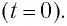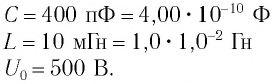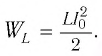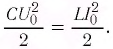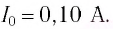Физика
В данной методической разработке колебания и волны – чрезвычайно обширная область физических явлений. Колебания (в механических и электромагнитных системах), волны (упругие и электромагнитные) — это учебный материал, который необходим для изучения специальных технических дисциплин в электротехническом ВУЗе.
Изучение колебаний начинается с изучения механических колебаний в различных механических колебательных системах. Использование электромеханических аналогий позволяет изучать электромагнитные колебания с точки зрения общих признаков колебаний, объединяя поведение механических и электромагнитных систем. Затем рассматриваются колебания связанных систем. Методически правильно и удобно начать изучение колебательных процессов с довольно простых систем с небольшим числом степеней свободы, а затем перейти к системам с бесконечно большим числом степеней свободы, какими являются волны.
Волны на воде, сейсмические, звуковые, световые, радиоволны – это далеко не все волновые процессы в природе. Главная цель данной разработки – ознакомление студентов с основными идеями, общими для всех волновых явлений, т.е. и для электромагнитных, и для упругих волн.
Некоторые вопросы прикладного характера или вопросы, связанные с уточнением применяемого математического аппарата, вынесены в приложения.
В конце работы приведен список литературных источников, из которых 3 — учебники, рекомендованные для ВУЗов, 5 – дополнительная литература по разделу “Колебания и волны”, 7 – справочники, 13 – методические разработки кафедры.
1. Колебательными процессами (колебаниями) называются движения или изменения состояния, обладающие той или иной степенью повторяемости во времени.
Колебания называются периодическими , если значения физических величин, изменяющиеся в процессе колебаний, повторяются через равные промежутки времени Т, называемые периодом . Математически это записывается так:
.
2. В зависимости от физической природы и механизма возбуждения колебаний различают:
— механические колебания (колебания маятников, струн, балок, частей машин и механизмов, качка кораблей, волнение моря, колебания давления при распространении звука в газе, жидкости, твердом теле и т.д.);
— электромагнитные колебания (переменный ток, колебания тока, заряда, векторов E и H в колебательных контурах и т.д.);
— электромеханические колебания (колебания мембран телефонов, диффузоров электродинамических громкоговорителей и т.д.).
3. Колебательные движения отличаются от других видов движений. Они характеризуются некоторыми общими признаками. На языке теории колебаний различия между колебательным движением тела и процессами в колебательных электромагнитных контурах исчезают, если подходить к ним с точки зрения общих принципов. Такой подход называется электромеханическими аналогиями.
4. Система, совершающая колебания, называется колебательной системой .
Колебания, которые возникают вследствие какого-либо начального отклонения системы от ее устойчивого равновесия, называются собственными колебаниями .
Колебания, возникающие в системе под влиянием переменного внешнего воздействия, называются вынужденными колебаниями .
5. Общие признаки и понятия, единые для различных колебательных систем, следующие:
- дифференциальное уравнение (его вид одинаков для любых колеблющихся систем);
- уравнение колебаний;
- амплитуда;
- частота или период колебаний;
- фаза;
- начальная фаза.
Рассмотрим колебания в механической и электромагнитной системах, выделяя именно перечисленные выше признаки.
Глава 1. СОБСТВЕННЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ.
§1.1. Механические гармонические колебания.
1. В качестве механической колебательной системы, на примере которой мы будем рассматривать колебания, выбираем пружинный маятник : маленькое тело (материальная точка) массой m подвешено на пружине с жесткостью k (Рисунок 2).
Ненагруженная пружина имела длину l 0 . Когда подвесили тело, пружина удлинилась на ∆l. Возникшая упругая сила уравновесила силу тяжести . Это соотношение позволяет определить положение равновесия пружинного маятника . Если теперь тело сместить относительно положения равновесия на расстояние х, то на тело будет действовать сила упругости и сила тяжести.
Равнодействующая этих сил равна:
Знак минус означает, что направление силы F упр. и направление смещения х противоположны. F упр. — сила упругости, возникающая при смещении тела относительно положения равновесия за счет сжатия или растяжения пружины (в зависимости от того, в какую сторону от положения равновесия отклонено тело). Качественно на Рисунке 1.1 виден результат действия упругой силы ( чем больше смещение, тем больше F упр. ).
Рисунок 1.1 – Положения пружинного маятника за время одного периода колебаний.
Если система совершает колебания под действием сил, развивающихся в самой колебательной системе без внешних воздействий и без учета сил сопротивления, то колебания называются незатухающими собственными колебаниями .
Отсутствие затухания колебаний характерно для идеальной колебательной системы, которая является физической моделью реальных физических процессов.
2. Дифференциальное уравнение , соответствующее колебаниям пружинного маятника, можно получить из закона его движения, которым является 2-й закон Ньютона m a = F .
Учитывая, что ускорение есть вторая производная от смещения по времени
,
а сила, действующая на тело, есть сила упругости, определяемая для малых смещений тела от положения равновесия по закону Гука, как , получим
Это дифференциальное уравнение второго порядка для незатухающих колебаний. Основной его отличительной особенностью является тот факт, что вторая производная от смещения по времени (т.е. ускорение) пропорциональна смещению. Дифференциальное уравнение, в которое величина х входит в нулевой или первой степени, называется линейным дифференциальным уравнением. В дальнейшем мы покажем, что подобного рода уравнения характерны для незатухающих колебаний в любой идеальной колебательной системе.
Перенесем все члены уравнения в левую часть и приведем дифференциальное уравнение к виду:
Величина , обозначим ее , получим
3. Решением дифференциального уравнения такого вида являются уравнения:
Эти решения называются уравнениями колебаний, они позволяют вычислить смещение х пружинного маятника в любой момент времени.
Колебания, при которых характеризующие их физические величины изменяются по закону синуса или косинуса, называются гармоническими .
Отличие аргументов функций синуса и косинуса составляет , т.е. .
В дальнейшем чаще всего мы будем использовать решение дифференциального уравнения в виде .
4. В уравнении колебаний:
А – амплитуда смещения – максимальное отклонение маятника от положения равновесия;
х – смещение маятника, т.е. отклонение колеблющейся точки (тела) от положения равновесия в момент времени t;
– фаза колебаний – величина, определяющая положение колеблющейся точки в любой момент времени t;
α – начальная фаза определяет положение маятника в начальный момент времени (t = 0).
Периодом T называется наименьший интервал времени, за который система возвращается в исходное положение. За период колебаний система совершает одно полное колебание.
Частотой периодических колебаний называется величина , равная числу колебаний, совершаемых за единицу времени.
Циклической или круговой частотой периодических колебаний называется величина , равная числу колебаний, совершаемых за единиц времени.
Для пружинного маятника частота и период собственных колебаний в зависимости от параметров системы имеют вид:
5. Зная уравнение смещения пружинного маятника, получим подобные уравнения для других физических величин. Найдем скорость, ускорение, энергию колебаний, если уравнение смещения пружинного маятника задано в виде .
Скорость колебаний маятника есть первая производная по времени от смещения:
Величина Аω 0 называется амплитудой скорости . Амплитуда – величина положительная (по определению).
Величина Аω 0 2 – амплитуда ускорения. И смещение, и ускорение маятника изменяются по закону косинуса, но отличаются, кроме амплитуды, еще и знаком. Направление ускорения совпадает с направлением упругой силы.
6. Так как собственные колебания в идеальной системе происходят без внешних воздействий, то колебательная система является замкнутой и для нее выполняется закон сохранения механической энергии.
Полная механическая энергия пружинного маятника равна:
Потенциальная энергия материальной точки, гармонически колеблющейся под действием упругой силы, равна:
Кинетическая энергия пружинного маятника равна
Полная энергия колебаний пружинного маятника равна
Частота изменений кинетической и потенциальной энергии в 2 раза больше частоты изменения смещения, скорости и ускорения. Соответственно период изменения этих видов энергии .
Графики физических величин в зависимости от времени представлены на Рисунке 1.2 в пределах двух периодов колебаний (начальная фаза взята равной нулю α = 0).
Рисунок 1.2 – Графики смещения (х), скорости (v), ускорения (а) в зависимости от времени t
§1.2. Зависимость амплитуды и начальной фазы колебаний от начальных условий.
Решения дифференциального уравнения колебаний определены с точностью до постоянной величины, поэтому таких решений бесчисленное множество. Выбор решения для данной конкретной колебательной системы можно сделать, если задать ее поведение в начальный момент времени, то есть начальные условия. Например, если просто отклонить маятник, растянув пружину, а затем спокойно отпустить его, или отклонить, а затем подтолкнуть маятник, то движения маятника будут различными. Рассмотрим зависимость параметров колебательной системы от начальных условий.
Пусть при t = 0 смещение системы от положения равновесия равно х 0 , а начальная скорость v 0 . Гармоническое колебание описывается уравнением .
При t = 0 имеем два уравнения:
Возведя в квадрат оба уравнения и сложив их, получим уравнение для амплитуды:
Поделив одно уравнение на другое, получим соотношение для начальной фазы:
Таким образом, и амплитуда, и начальная фаза колебаний зависят от начальных условий колебательной системы.
§1.3. Свободные гармонические колебания в LC-контуре.
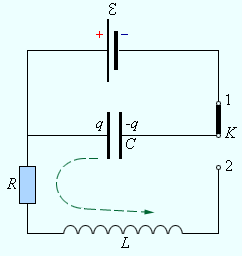
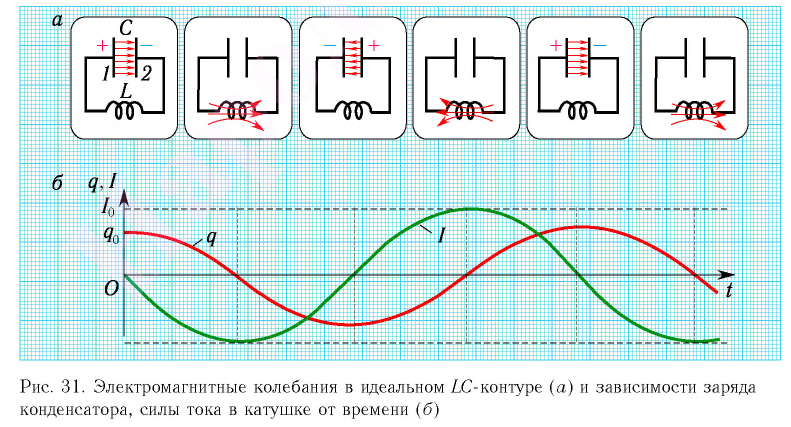
1. Электромагнитный контур состоит из плоского конденсатора емкостью С и катушки индуктивности (соленоида) с индуктивностью L. Такой контур называется идеальным контуром с распределенными параметрами . Конденсатор зарядили, на одной пластине заряд +q, на другой (–q). Рассмотрим процессы в LC – контуре за время T, называемое периодом колебаний.
Момент времени t = 0. Конденсатор заряжен, ключ “К” разомкнут, ток в контуре не идет:
I = 0, ,
Ключ замкнут, по цепи идет ток разрядки до тех пор, пока не выровняются потенциалы обкладок конденсатора. При
Когда конденсатор разрядится, ток разрядки прекратится. Магнитное поле в катушке индуктивности, не поддерживаемое током, начнет уменьшаться. Уменьшение магнитного поля вызовет уменьшение магнитного потока сквозь площадь катушки, возникнет ЭДС индукции. По цепи контура пойдет индукционный ток того же направления, что и ток разрядки (правило Ленца). Это приведет к перезарядке конденсатора. При
Направление тока разрядки в контуре изменится. Ток разрядки будет идти по цепи до выравнивания потенциалов на обкладках конденсатора.
При t = T система вернется в исходное положение.
В рассмотренном LC – контуре происходит превращение энергии из одного вида в другой и обратно, полная энергия контура — величина постоянная .
Периодические изменения вектора напряженности Е электрического поля и вектора магнитной индукции В магнитного поля в закрытом колебательном LC – контуре называется электромагнитными колебаниями .
2. Используем 2-й закон Кирхгофа для получения дифференциального уравнения электромагнитных колебаний.
Для любого замкнутого контура алгебраическая сумма падений напряжений на всех его участках равна алгебраической сумме ЭДС, действующих в этом контуре (2-ой закон Кирхгофа).
Падение напряжения на обкладках конденсатора в LC – контуре равно
где q – величина заряда на обкладках, С – емкость конденсатора. ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, определяется формулой: (закон Фарадея для самоиндукции).
Второй закон Кирхгофа для LC – контура имеет вид:
По определению сила тока равна первой производной по времени от заряда , тогда .
Преобразуем уравнение 2-ого закона Кирхгофа, получим
Обозначим , получим окончательно уравнение вида:
Это линейное дифференциальное уравнение второго порядка, решениями которого являются уравнения:
И дифференциальное уравнение для электромагнитных колебаний, и его решения подобны тем, которые получены для механической системы (пружинного маятника).
Величины, входящие в уравнения электромагнитных колебаний, имеют следующий смысл:
q 0 – амплитуда заряда – максимальный заряд конденсатора;
q – величина заряда на обкладках конденсатора в момент времени t;
– фаза колебаний – величина, определяющая заряд конденсатора в любой момент времени t;
α – начальная фаза определяет заряд конденсатора в начальный момент времени (t = 0).
Циклической частотой периодических колебаний в LC – контуре является величина .
Период колебаний равен ( формула Томсона ).
Определим зависимость силы тока, ЭДС и энергии колебаний от времени в LC – контуре. Уравнение изменения заряда на обкладках конденсатора возьмем в виде:
Сила тока в контуре определяется соотношением:
Величину называют амплитудой силы тока.
Уравнение для ЭДС имеет вид:
Величина – амплитуда ЭДС .
Электрическая и магнитная энергия изменяется согласно уравнениям:
Полная энергия колебаний в LC — контуре не зависит от времени (закон сохранения энергии).
Графики зависимостей от времени t физических величин, характеризующих электромагнитных колебаний в LC – контуре, аналогичны графикам для механических колебаний (см. Рисунок 1.2).
Если заряд на обкладках изменяется по закону , т.е. начальная фаза α = 0, то его график такой же как график смещения.
Напряжение между обкладками конденсатора изменяется по тому же закону, что и заряд конденсатора, только амплитуда напряжения будет другой .
Изменение силы тока аналогично изменению скорости тела при механических незатухающих колебаниях. W эл. изменяется как W пот. , а W магн. — как W кин. .
§1.4. Графическое изображение гармонических колебаний. Векторная диаграмма.
Решение многих вопросов в теории колебаний значительно упрощается, если использовать графический метод изображения гармонических колебаний в виде векторов на плоскости. Такое изображение называется векторной диаграммой колебаний (Рисунок 1.3).
Рисунок 1.3 – Векторная диаграмма гармонического колебаний .
Последовательность построения векторной диаграммы колебания, заданного уравнением , такова:
- Выберем на плоскости ось Х, на ней возьмем точку О – начало координат.
- Под углом α, равном начальной фазе колебаний, к оси Х, из точки О откладываем вектор, равный по длине амплитуде А колебаний.
- Вектор А равномерно вращаем вокруг точки О против часовой стрелки с угловой скоростью, равной циклической частоте колебаний.
Тогда в любой момент времени угол вектора А с осью Х равен . Соответственно проекция конца вектора А на ось Х будет совершать колебания по закону , а сама проекция вектора А в любой момент времени будет равна смещению х колеблющейся точки от положения равновесия. Если начальная фаза колебаний , то в начальный момент времени вектор А откладываем из точки О вдоль направления оси Х.
Глава 2. СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
Одно и то же тело может одновременно участвовать в двух и более движениях. Простым примером является движение шарика, брошенного под углом к горизонту. Можно считать, что шарик участвует в двух независимых взаимно перпендикулярных движениях: равномерном по горизонтали и равнопеременном по вертикали. Одно и то же тело (материальная точка) может участвовать в двух (и более) движениях колебательного типа.
Под сложением колебаний понимают определение закона результирующего колебания, если колебательная система одновременно участвует в нескольких колебательных процессах. Различают два предельных случая – сложение колебаний одного направления и сложение взаимно перпендикулярных колебаний.
§2.1. Сложение гармонических колебаний одного направления.
1. Сложение двух колебаний одного направления (сонаправленных колебаний)
можно провести с помощью метода векторных диаграмм (Рисунок 9) вместо сложения двух уравнений.
На Рисунке 2.1 показаны векторы амплитуд А 1 (t) и А 2 (t) складываемых колебаний в произвольный момент времени t, когда фазы этих колебаний соответственно равны и . Сложение колебаний сводится к определению . Воспользуемся тем фактом, что на векторной диаграмме сумма проекций складываемых векторов равна проекции векторной суммы этих векторов.
Результирующему колебанию соответствует на векторной диаграмме вектор амплитуды и фаза .
Рисунок 2.1 – Сложение сонаправленных колебаний.
Величина вектора А (t) может быть найдена по теореме косинусов:
Фаза результирующего колебания задается формулой:
Если частоты складываемых колебаний ω 1 и ω 2 не равны, то и фаза φ(t), и амплитуда А (t) результирующего колебания будут изменяться с течением времени. Складываемые колебания называются некогерентными в этом случае.
2. Два гармонических колебания x 1 и x 2 называются когерентными , если разность их фаз не зависит от времени:
Но так как , то для выполнения условия когерентности двух этих колебаний должны быть равны их циклические частоты .
Амплитуда результирующего колебания, полученного при сложении сонаправленных колебаний с равными частотами (когерентных колебаний) равна:
Начальную фазу результирующего колебания легко найти, если спроектировать векторы А 1 и А 2 на координатные оси ОХ и ОУ (см. Рисунок 9):
Итак, результирующее колебание, полученное при сложении двух гармонических сонаправленных колебаний с равными частотами, также является гармоническим колебанием .
3. Исследуем зависимость амплитуды результирующего колебания от разности начальных фаз складываемых колебаний.
Если , где n – любое целое неотрицательное число
(n = 0, 1, 2…), то , т.е. результирующая амплитуда будет минимальной . Складываемые колебания в момент сложения находились в противофазе . При результирующая амплитуда равна нулю .
Если , то , т.е. результирующая амплитуда будет максимальной . В момент сложения складываемые колебания находились в одной фазе , т.е. были синфазны . Если амплитуды складываемых колебаний одинаковы , то .
4. Сложение сонаправленных колебаний с неравными, но близкими частотами .
Частоты складываемых колебаний не равны , но разность частот много меньше и ω 1 , и ω 2 . Условие близости складываемых частот записывается соотношениями .
Примером сложения сонаправленных колебаний с близкими частотами является движение горизонтального пружинного маятника, жесткость пружин которого немного различна k 1 и k 2 .
Пусть амплитуды складываемых колебаний одинаковы , а начальные фазы равны нулю . Тогда уравнения складываемых колебаний имеют вид:
Результирующее колебание описывается уравнением:
Получившееся уравнение колебаний зависит от произведения двух гармонических функций: одна – с частотой , другая – с частотой , где ω близка к частотам складываемых колебаний (ω 1 или ω 2 ). Результирующее колебание можно рассматривать как гармоническое колебание с изменяющейся по гармоническому закону амплитудой. Такой колебательный процесс называется биениями . Строго говоря, результирующее колебание в общем случае не является гармоническим колебанием.
Абсолютное значение косинуса взято потому, что амплитуда – величина положительная. Характер зависимости х рез. при биениях показан на Рисунке 2.2.
Рисунок 2.2 – Зависимость смещения от времени при биениях.
Амплитуда биений медленно меняется с частотой . Абсолютное значение косинуса повторяется, если его аргумент изменяется на π, значит и значение результирующей амплитуды повторится через промежуток времени τ б , называемый периодом биений (см. Рисунок 12). Величину периода биений можно определить из следующего соотношения:
Величина — период биений.
Величина есть период результирующего колебания (Рисунок 2.4).
§2.2. Сложение взаимно перпендикулярных колебаний.
1. Модель, на которой можно продемонстрировать сложение взаимно перпендикулярных колебаний, представлена на Рисунке 2.3. Маятник (материальная точка массой m) может совершать колебания по осям ОХ и ОУ под действием двух сил упругости, направленных взаимно перпендикулярно.
Складываемые колебания имеют вид:
Частоты колебаний определяются как , , где , -коэффициенты жесткости пружин.
2. Рассмотрим случай сложения двух взаимно перпендикулярных колебаний с одинаковыми частотами , что соответствует условию (одинаковые пружины). Тогда уравнения складываемых колебаний примут вид:
Когда точка участвует одновременно в двух движениях, ее траектория может быть различной и достаточно сложной. Уравнение траектории результирующего колебаний на плоскости ОХУ при сложении двух взаимно перпендикулярных с равными частотами можно определить, исключив из исходных уравнений для х и y время t:
Вид траектории определяется разностью начальных фаз складываемых колебаний, которые зависят от начальных условий (см. § 1.1.2). Рассмотрим возможные варианты.
а) Если , где n = 0, 1, 2…, т.е. складываемые колебания синфазные, то уравнение траектории примет вид:
Рисунок 2.3.а
Рисунок 2.3 б
б) Если (n = 0, 1, 2 …), т.е. складываемые колебаний находятся в противофазе, то уравнение траектории записывается так:
В обоих случаях ( а, б) результирующее движение точки будет колебание по прямой, проходящей через точку О. Частота результирующего колебания равна частоте складываемых колебаний ω 0 , амплитуда определяется соотношением:
Угол, который прямая (траектория) составляет с осью ОХ, можно найти из уравнения:
(знак “плюс” – случай а, знак “минус” – случай б).
Результатом сложения взаимно перпендикулярных колебаний (случай а и б) является колебание, которое называется линейно поляризованным .
в) Если (n = 0, 1, 2 …), то уравнение траектории результирующего движения примет вид:
Это уравнение эллипса, его оси совпадают с осями координат ОХ и ОУ, а размеры его полуосей равны и (Рисунок 2.4 ).
Точка в результате участия в двух взаимно перпендикулярных колебаниях описывает эллипс за время, равное периоду складываемых колебаний .
3. Сложение взаимно перпендикулярных колебаний с кратными частотами .
Складываются взаимно перпендикулярные колебания, частоты которых не равны , но , , где a и b – целые числа.
Периоды колебаний вдоль осей ОХ и ОУ соответственно равны и . Отношение периодов .
Траектория точки, участвующей во взаимно перпендикулярных колебаниях с кратными частотами, — замкнутая кривая, форма которой зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Такие замкнутые траектории называются фигурами Лиссажу.
Глава 3. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ.
Затуханием колебаний называется постепенное уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Собственные колебания без затухания – это идеализация. Причины затухания могут быть разные. В механической системе к затуханию колебаний приводит наличие трения. В электромагнитном контуре к уменьшению энергии колебаний приводят тепловые потери в проводниках, образующих систему. Когда израсходуется вся энергия, запасенная в колебательной системе, колебания прекратятся. Поэтому амплитуда затухающих колебаний уменьшается, пока не станет равной нулю.
Затухающие колебания, как и собственные, в системах, разных по своей природе, можно рассматривать с единой точки зрения – общих признаков. Однако, такие характеристики, как амплитуда и период, требуют переопределения, а другие – дополнения и уточнения по сравнению с такими же признаками для собственных незатухающих колебаний. Общие признаки и понятия затухающих колебаний следующие:
Дифференциальное уравнение должно быть получено с учетом убывания в процессе колебаний колебательной энергии.
Уравнение колебаний – решение дифференциального уравнения.
Амплитуда затухающих колебаний зависит от времени.
Частота и период зависят от степени затухания колебаний.
Фаза и начальная фаза имеют тот же смысл, что и для незатухающих колебаний.
§3.1. Механические затухающие колебания.
Механическая система : пружинный маятник с учетом сил трения.
Силы, действующие на маятник :
Упругая сила . , где k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.
Сила сопротивления . Рассмотрим силу сопротивления, пропорциональную скорости v движения (такая зависимость характерна для большого класса сил сопротивления): . Знак “минус” показывает, что направление силы сопротивления противоположно направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:
Закон движения пружинного маятника – это второй закон Ньютона:
m a = F упр. + F сопр.
Учитывая, что и , запишем второй закон Ньютона в виде:
Разделив все члены уравнения на m, перенеся их все в правую часть, получим дифференциальное уравнение затухающих колебаний:
Обозначим , где β – коэффициент затухания , , где ω 0 – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.
В новых обозначениях дифференциальное уравнение затухающих колебаний имеет вид:
Это линейное дифференциальное уравнение второго порядка.
Уравнение затухающих колебаний есть решение такого дифференциального уравнения:
В приложении 1 показано получение решения дифференциального уравнения затухающих колебаний методом замены переменных.
Частота затухающих колебаний :
(физический смысл имеет только вещественный корень, поэтому ).
Период затухающих колебаний :
Смысл, который вкладывался в понятие периода для незатухающих колебаний, не подходит для затухающих колебаний, так как колебательная система никогда не возвращается в исходное состояние из-за потерь колебательной энергии. При наличии трения колебания идут медленнее: .
Периодом затухающих колебаний называется минимальный промежуток времени, за который система проходит дважды положение равновесия в одном направлении.
Для механической системы пружинного маятника имеем:
Амплитуда затухающих колебаний :
, для пружинного маятника .
Амплитуда затухающих колебаний – величина не постоянная, а изменяющаяся со временем тем быстрее, чем больше коэффициент β. Поэтому определение для амплитуды, данное ранее для незатухающих свободных колебаний, для затухающих колебаний надо изменить.
При небольших затуханиях амплитудой затухающих колебаний называется наибольшее отклонение от положения равновесия за период.
Графики зависимости смещения от времени и амплитуды от времени представлены на Рисунках 3.1 и 3.2.
Рисунок 3.1 – Зависимость смещения от времени для затухающих колебаний.
Рисунок 3.2 – Зависимости амплитуды от времени для затухающих колебаний
§3.2. Электромагнитные затухающие колебания.
Электромагнитные затухающие колебания возникают в э лектромагнитной колебательной систему , называемой LCR – контур (Рисунок 3.3).
Дифференциальное уравнение получим с помощью второго закона Кирхгофа для замкнутого LCR – контура: сумма падений напряжения на активном сопротивлении (R) и конденсаторе (С) равна ЭДС индукции, развиваемой в цепи контура:
— на активном сопротивлении: , где I – сила тока в контуре;
— на конденсаторе (С): , где q – величина заряда на одной из обкладок конденсатора.
ЭДС, развиваемая в контуре – это ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, а следовательно, и магнитного потока сквозь ее сечение: (закон Фарадея).
Подставим значения U R , U C , в уравнение, отражающее закон Кирхгофа, получим:
Сила тока определяется как производная от заряда , тогда , и дифференциальное уравнение примет вид:
Обозначим , , получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:
Решение дифференциального уравнения или уравнение колебаний для заряда на обкладках конденсатора имеет вид:
Амплитуда затухающих колебаний заряда имеет вид:
Частота затухающих колебаний в LCR – контуре:
Период затухающих электромагнитных колебаний:
Возьмем уравнение для заряда в виде , тогда уравнение для напряжения на обкладках конденсатора можно записать так
.
Величина называется амплитудой напряжения на конденсаторе .
Ток в контуре меняется со временем. Уравнение для силы тока в контуре можно получить, используя соотношение и векторную диаграмму.
Окончательное уравнение для силы тока таково:
где — начальная фаза.
Она не равна α, так как сила тока изменяется не по синусу, что дала бы производная от заряда, а по косинусу.
Энергия колебаний в контуре складывается из энергии электрического поля
и энергии магнитного поля
Полная энергия в любой момент времени:
где W 0 – полная энергия контура в момент времени t=0 .
§3.3. Характеристики затухающих колебаний.
1. Коэффициент затухания β.
Изменение амплитуды затухающих колебаний происходит по экспоненциальному закону:
Пусть за время τ амплитуда колебаний уменьшится в “e ” раз (“е” – основание натурального логарифма, е ≈ 2,718). Тогда, с одной стороны, , а с другой стороны, расписав амплитуды А зат. (t) и А зат. (t+τ), имеем . Из этих соотношений следует βτ = 1, отсюда
Промежуток времени τ, за который амплитуда уменьшается в “е” раз, называется временем релаксации.
Коэффициент затухания β – величина, обратно пропорциональная времени релаксации.
2. Логарифмический декремент затухания δ — физическая величина, численно равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих по времени на период .
Если затухание невелико, т.е. величина β мала, то амплитуда незначительно изменяется за период, и логарифмический декремент можно определить так:
где А зат. (t) и А зат. (t+NT) – амплитуды колебаний в момент времени е и через N периодов, т.е.в момент времени (t + NT).
3. Добротность Q колебательной системы – безразмерная физическая величина, равная произведению величины (2π) νа отношение энергии W(t) системы в произвольный момент времени к убыли энергии за один период затухающих колебаний:
Так как энергия пропорциональна квадрату амплитуды, то
При малых значениях логарифмического декремента δ добротность колебательной системы равна
где N e – число колебаний, за которое амплитуда уменьшается в “е” раз.
Так, добротность электромагнитной системы LCR – контура при малом затухании колебаний равна , а добротность пружинного маятника — .Чем больше добротность колебательной системы, тем меньше затухание, тем дольше будет длиться периодический процесс в такой системе.
4. При увеличении коэффициента β, частота затухающих колебаний уменьшает-ся, а период увеличивается. При ω 0 = β частота затухающих колебаний становится равной нулю ω зат. = 0, а Т зат. = ∞. При этом колебания теряют периодический характер и называются апериодическими.
При ω 0 = β параметры системы, ответственные за убывание колебательной энергии, принимают значения, называемые критическими . Для пружинного маятника условие ω 0 = β запишется так: , откуда найдем величину критического коэффициента сопротивления:
Для LCR – контура условие позволяет вычислить критическое сопротивление контура , при котором колебания потеряют свою периодичность:
Глава 4. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ.
До сих пор мы изучали процессы в механических системах под действием сил, развивающихся в самих системах. Каково будет поведение колебательных систем, к которым тем или иным способом приложена внешняя сила? Для электромагнитного контура аналогичная ситуация возникнет, если в цепь контура включить внешний источник ЭДС.
Рассмотрим явление колебаний, если внешняя (вынуждающая) сила или внешняя ЭДС изменяется в зависимости от времени по гармоническому закону. При этом в системах возникнут колебания, характер которых в той или иной мере повторит характер вынуждающей силы или ЭДС источника. Такие колебания называются вынужденными .
Рассматривая свободные колебания в механической и электромагнитной системах, мы убедились в полной аналогии законов колебаний. Такое же сходство наблюдали для механических и электромагнитных затухающих колебаний. Следует ожидать аналогии законов в механической и электромагнитной системах и при вынужденных колебаниях.
§4.1. Общие признаки вынужденных механических и электромагнитных колебаний.
1. Рассмотрим вынужденные механические колебаний пружинного маятника, на который действует внешняя ( вынуждающая ) периодическая сила . Силы, которые действуют на маятник, однажды выведенный из положения равновесия, развиваются в самой колебательной системе. Это сила упругости и сила сопротивления .
Закон движения (второй закон Ньютона) запишется следующим образом:
Разделим обе части уравнения на m, учтем, что , и получим дифференциальное уравнение вынужденных колебаний:
Обозначим (β – коэффициент затухания ), (ω 0 – частота незатухающих свободных колебаний), сила, действующая на единицу массы. В этих обозначениях дифференциальное уравнение вынужденных колебаний примет вид:
Это дифференциальное уравнение второго порядка с правой частью, отличной от нуля. Решение такого уравнения есть сумма двух решений
– общее решение однородного дифференциального уравнения, т.е. дифференциального уравнения без правой части, когда она равна нулю. Такое решение нам известно – это уравнение затухающих колебаний, записанное с точностью до постоянной, значение которой определяется начальными условиями колебательной системы:
Мы обсуждали ранее, что решение может быть записано через функции синуса.
Если рассматривать процесс колебаний маятника через достаточно большой промежуток времени Δt после включения вынуждающей силы (Рисунок 22), то затухающие колебания в системе практически прекратятся. И тогда решением дифференциального уравнения с правой частью будет решение .
Решение — это частное решение неоднородного дифференциального уравнения, т.е. уравнения с правой частью. Из теории дифференциальных уравнений известно, что при правой части, изменяющейся по гармоническому закону, решение будет гармонической функцией (sin или cos) с частотой изменения, соответствующей частоте Ω изменения правой части:
где А ампл. – амплитуда вынужденных колебаний, φ 0 – сдвиг фаз , т.е. разность фаз между фазой вынуждающей силы и фазой вынужденных колебаний. И амплитуда А ампл. , и сдвиг фаз φ 0 зависят от параметров системы (β, ω 0 ) и от частоты вынуждающей силы Ω.
Период вынужденных колебаний равен .
График вынужденных колебаний на Рисунке 4.1.
Рисунок 4.1 – График вынужденных колебаний.
2. Электромагнитные вынужденные колебания .
Электромагнитная система, в которой развиваются вынужденные колебания, — это LCR – контур с включенным в него внешним источником. Рассмотрим случай, когда ЭДС источника изменяется по гармоническому закону:
Конденсатор, как рассматривалось ранее, заряжен и при его разрядке в контуре будет идти изменяющийся по времени электрический ток, что вызовет появление в катушке индуктивности ЭДС индукции ( ). Согласно второму закону Кирхгофа имеем:
где U C , U R – соответственно падение напряжения на конденсаторе и активном сопротивлении.
Учитывая, что , где I – сила тока в контуре, , где q – величина заряда на одной из обкладок конденсатора, — ЭДС индукции, запишем закон Кирхгофа в виде:
Записывая соотношения и , и преобразуя уравнение для закона Кирхгофа, мы получим дифференциальное уравнение вынужденных электромагнитных колебаний в виде:
Окончательно дифференциальное уравнений (при использовании обозначений , ) примет вид:
Вид дифференциального уравнения вынужденных электромагнитных колебаний такой же, как и вид дифференциального уравнения для вынужденных колебаний в механической системе. Это дифференциальное уравнение второго порядка с правой частью , поэтому все, что говорилось относительно его решений для механических колебаний верно и для электромагнитной системы. Сначала в системе возникнут и затухающие, и вынужденные колебания, но спустя некоторый промежуток времени, переходный процесс закончится и в системе установятся вынужденные колебаний с той же частотой, что и частота изменения ЭДС источника:
φ 0 — сдвиг фаз между изменением заряда конденсатора и действием внешней ЭДС источника.
§4.2. Зависимости амплитуды вынужденных колебаний и сдвига фаз от частоты внешнего воздействия. Резонанс.
1. Вернемся к механической системе пружинного маятника, на который действует внешняя сила, изменяющаяся по гармоническому закону. Для такой системы дифференциальное уравнение и его решение соответственно имеют вид:
Проанализируем зависимость амплитуды колебаний и сдвига фаз от частоты внешней вынуждающей силы, для этого найдем первую и вторую производную от х и подставим в дифференциальное уравнение.
Воспользуемся методом векторной диаграммы. Из уравнения видно, что сумма трех колебаний в левой части уравнения (Рисунок 4.1) должна быть равна колебанию в правой части. Векторная диаграмма выполнена для произвольного момента времени t. Из нее можно определить .
Учитывая значение , , , получим формулы для φ 0 и А ампл. механической системы:
2. Исследуем зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы и величины силы сопротивления в колеблющейся механической системе, по этим данным построим график . Результаты исследования отражены в Рисунке 4.2, по ним видно, что при некоторой частоте вынуждающей силы амплитуда колебаний резко возрастает. И это возрастание тем больше, чем меньше коэффициент затухания β. При амплитуда колебаний становится бесконечно большой .
Явление резкого возрастания амплитуды вынужденных колебаний при частоте вынуждающей силы, равной , называется резонансом.
Кривые на Рисунке 4.2 отражают зависимость и называются амплитудными резонансными кривыми .
Рисунок 4.2 – Графики зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы.
3. Используем данные об амплитуде и сдвиге фаз вынужденных колебаний для механической системы и выразим эти же характеристики для аналогичных величин электромагнитной системы (LCR– контур с включенным в его цепь внешним источником ЭДС, величина которой изменяется по гармоническому закону):
5. Сила тока при установившихся в контуре колебаниях равна:
где — амплитуда силы тока, ψ 0 – сдвиг фаз между силой тока и внешнейЭДС в контуре. Амплитуда силы тока и ψ 0 находятся по формулам:
График зависимости представлен на Рисунке 4.3.
Решение дифференциального уравнения затухающих колебаний.
Дифференциальное уравнение затухающих колебаний имеет вид:
Это линейное дифференциальное уравнение решается заменой переменных. Представим функцию х, зависящую от времени t, в виде:
Найдем первую и вторую производную этой функции от времени, учитывая, что функция z также является функцией времени:
Подставим выражения в дифференциальное уравнение:
Приведем подобные члены в уравнении и сократим каждый член на , получим уравнение:
Решением уравнения являются функции , .
Возвращаясь к переменной х, получим формулы уравнений затухающих колебаний:
Хотя Международная система единиц рекомендуется для всех областей науки и техники, в акустике широкое применение сохранила система СГС. Ниже мы приводим важнейшие акустические величины в СИ и даем их связь с системой СГС.
Таблица 2 -Объективные характеристики механических волновых процессов.
Величина и ее обозначение
Уравнение для определения единицы измерения
Единица измерения
Сокращенное обозначение
Частота
Звуковое давление р
ньютон на квадратный метр
(паскаль)
Плотность звуковой энергии
джоуль на кубический метр
Поток звуковой энергии (звуковая мощность)
Интенсивность звука I
Ватт на квадратный метр
В таблице 3 приведены некоторые акустические единицы системы СГС и их связь с единицами СИ.
Величина
Единица измерения и ее связь с единицами СИ
Звуковое давление
Плотность звуковой энергии
Звуковая мощность
Интенсивность звука
Для характеристики величин, определяющих восприятие звука, существенными являются не столько абсолютные значения интенсивности звука и звукового давления, сколько их отношение к некоторым пороговым значениям. Поэтому вводятся понятие относительных уровней интенсивности и звукового давления.
Для того, чтобы звуковая волна воспринималась на слух, необходимо, чтобы ее интенсивность превышала бы минимальную величину , называемую порогом слышимости. Величина различная для разных частот. Для частоты порог слышимости составляет величину порядка . Опытом установлено, что на каждой частоте есть верхняя граница силы звука , при превышении которого у человека возникают болевые ощущения. Величина называется порогом болевого ощущения.
Уровень интенсивности (уровень силы звука) равен десятичному логарифму отношения интенсивности звука при данной частоте к интенсивности звука при той же частоте на пороге слышимости:
Уровень громкости равен десятичному логарифму отношения интенсивности звука при данной частоте к интенсивности звука при частоте 1000 Гц на пороге слышимости:
Единицей измерения уровня интенсивности является бел (Б): . Одна десятая часть бела называется децибел (дБ): 0,1Б = 1дБ. Формула для определения уровня интенсивности в децибелах примет вид:
Если записать формулу для уровня громкости в виде , то единицей измерения в СИ при таком определении величины является, единица, имеющая название фон . При частоте 1000 Гц шкала фонов и децибел совпадают, для других частот они различны.
Уровень звукового давления равен произведению 20 на логарифм отношения звукового давления при данной частоте к звуковому давлению на пороге слышимости. Единицей измерения в данном случае является децибел.
- Савельев И.В. Курс общей физики. – М.: Наука, 1980, т 1, с.307.
- Савельев И.В. Курс общей физики. – М.: Наука, 1981 т 2, с.295.
- Яворский Б.М., Детлаф. Физика. – М.: Дрофа, 1998, с.795.
- Ф.Крауфорд. Берклиевский курс. Волны. – М.: Наука, 1974,с.527.
- Калашников С.Г. Электричество. – М.: Наука, 1964, с.666.
- Александров Н.В., Яшкин А.Я. Механика. – М.: Просвещение, 1978, с.416.
- Советский энциклопедический словарь. – М.: Советская энциклопедия, 1985.
- Физический энциклопедический словарь. –М.: Советская энциклопедия, 1984.
- Сена Л.А. Единицы физических величин и их размерности. – М.: Наука, 1977, с.335.
- Математическое введение в курс физики (часть 1). Под редакцией Пинегиной Т.Ю. – Новосибирск: Издательство СибГУТИ, 1998, с.72.
- Лисейкина Т.А., Пинегина Т.Ю., Серебрякова Т.К., Хайновская В.В. Методические указания по курсу физики для студентов заочников. – Новосибирск: Издательство НЭИС, 1992, с.57.
- Лисейкина Т.А., Пинегина Т.Ю.. Методические указания к решению задач по курсу физики средней школы (часть 2). – Новосибирск: Изд-во СибГУТИ, 1998, с.45.
- Сборник индивидуальных заданий по физике (часть 2). Под редакцией Серебряковой Т.К. – Новосибирск: Изд-во СибГУТИ (в печати).
- Физика в задачах, вопросах и ответах (часть 1). – Новосибирск: Издательство НЭИС, 1991, с.112.
- Физика в задачах, вопросах и ответах (часть 2). – Новосибирск: Издательство НЭИС, 1992, с.89.
Видео:2020 г. Дифференциальные уравнения для электрических цепей. Лекция и практикаСкачать

RLC-контур. Свободные колебания
Видео:Урок 353. Колебательный контурСкачать

R L C -контур
Кроме как в механических системах, к примеру, в таких, маятник или же грузило на пружине, свободные колебания могут возникать также и в электрических цепях, самым простым примером чего может послужить последовательный R L C -контур, изображенный на рис. 2 . 2 . 1 .
Рисунок 2 . 2 . 1 . Последовательный R L C -контур.
Находясь в положении 1 , ключ К позволяет источнику зарядить конденсатор до некоего напряжения δ . Процесс разрядки ранее заряженного конденсатора провоцируется переключением ключа К во второе положение и происходит через катушку индуктивности L и резистор R . При выполнении определенных условий данный процесс может приобретать характер колебательного.
Для не содержащей внешнего источника тока замкнутой R L C -цепи закон Ома представляет из себя выражение:
J R + U = — L d J d t .
В данной формуле U = q C – напряжение на конденсаторе, q является обозначением заряда конденсатора, а J = d q d t – ток в цепи. Правой частью соотношения является выражение ЭДС самоиндукции катушки. В случае, когда заряд конденсатора q ( t ) берется как переменная величина, описывающее свободные колебания в R L C -контуре уравнение может быть приведено к виду:
q · · + R L q · + 1 L C q = 0 .
Для начала рассмотрим такую ситуацию, в которой электромагнитные потери энергии в контуре равны нулю. В таком случае:
q · · + ω 0 2 q = 0 .
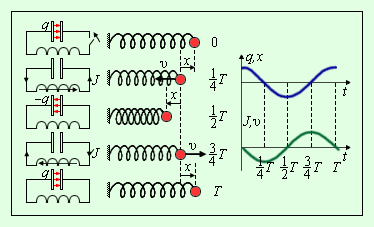
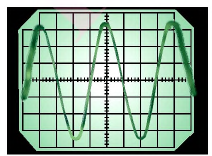
Примем обозначение ω 0 2 = 1 L C . Данным чуть выше уравнением описывается процесс незатухающих свободных колебаний в L C — контуре. Внешне оно полностью эквивалентно уравнению свободных колебаний груза на пружине в условиях отсутствующих сил трения. Аналогичный свободным механическим и электрическим колебаниям процесс изображен на рисунке 2 . 2 . 2 . На данной иллюстрации приводятся графики зависимости заряда смещения x ( t ) груза и q ( t ) конденсатора от положения равновесия, а также графики изменений тока J ( t ) и скорости груза υ ( t ) за период T = 2 π ω 0 колебаний.
Рисунок 2 . 2 . 2 . Аналогия процессов свободных электрических и механических колебаний.
Сделать заключение о некой связи между механическими и электрическими величинами нам позволяет сопоставление процессов в электрическом колебательном контуре и свободных колебаний груза на пружине. Данные аналогии показаны в таблице.
| Электрические величины | Механические величины | ||
| Заряд конденсатора | q ( t ) | Координата | x ( t ) |
| Ток в цепи | J = d q d t | Скорость | ν = d x d t |
| Индуктивность | L | Масса | m |
| Величина, обратная электроемкости | 1 C | Жесткость | k |
| Напряжение на конденсаторе | U = q C | Упругая сила | k x |
| Энергия электрического поля конденсатора | q 2 2 C | Потенциальная энергия пружины | k x 2 2 |
| Магнитная энергия катушки | L I 2 2 | Кинетическая энергия | m ν 2 2 |
| Магнитный поток | L I | Импульс | m υ |
Видео:Колебательный контур | ЕГЭ Физика | Николай НьютонСкачать

Свободные колебания
Свободные колебания в электрическом контуре носят название гармонических при условии отсутствия затухания.
Такие колебания происходят по закону:
q ( t ) = q 0 cos ( ω t + φ 0 ) .
Параметры L и C колебательного контура определяют лишь собственную частоту свободных колебаний:
«Начальными условиями», определяющими амплитуду q 0 и начальную фазу φ 0 , называют тот способ, при помощи которого систему вывели из равновесия.
Например, для процесса колебаний, который начнется в контуре, изображенном на рисунке 2 . 2 . 1 , после перевода ключа K в второе положение, q 0 = C δ , φ 0 = 0 .
Процесс свободных колебаниях провоцирует повторяющееся превращение запасенной в конденсаторе электрической энергии W э в магнитную энергию катушки W м и наоборот. В ситуации, когда потери энергии равны нулю, полная электромагнитная энергия системы не претерпевает изменений:
W = W э + W м = q 2 2 C + L J 2 2 = c o n s t
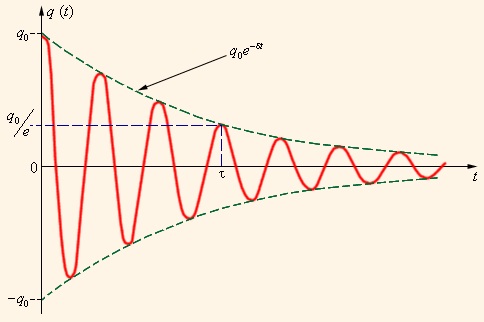
Однако любой реально существующий контур, в отличие от идеального, включает в себя некоторое сопротивление R . По этой причине, процесс свободных колебаний в подобном контуре не подчиняется гармоническому закону. Запасенная в контуре энергия с каждым периодом колебаний теряется, превращаясь в джоулево тепло, из-за чего колебания становятся затухающими (рис. 2 . 2 . 3 ).
Рисунок 2 . 2 . 3 . Затухающие колебания в контуре.
Затухающие колебания в электрическом контуре сравнимы с затухающими колебаниями груза на пружине в условиях существующего вязкого трения, при котором сила трения меняет свое значение прямо пропорционально скорости тела: F т р = – β υ .
В данной формуле сопротивление R электрического контура аналогично коэффициенту β . Уравнение свободных колебаний в контуре при наличии затухания принимает следующий вид:
q · · + 2 δ q · + ω 0 2 q = 0
Коэффициентом затухания называется физическая величина δ = R 2 L .
Следующая функция представляет собой решение приведенного выше дифференциального уравнения:
q ( t ) = q 0 e — δ t cos ( ω t + φ 0 ) ,
Также она содержит описывающий затухание колебаний множитель e x p ( – δ t ) . Скорость затухания зависит от электрического сопротивления R контура.
Интервал времени τ = 1 δ , в течение которого амплитуда колебаний уменьшается в e ≈ 2 , 7 раза, называется временем затухания.
Понятие добротности Q колебательной системы:
где N является числом полных колебаний, которые совершает система за время затухания τ .
Любая добротность Q , относящаяся к колебательной системе, которая способна совершать свободные колебания, имеет следующее энергетическое определение:
Q = 2 π З а п а с э н е р г и и в к о л е б а т е л ь н о й с и с т е м е П о т е р я э н е р г и и з а 1 п е р и о д
Добротность Q , принадлежащая R L C -контуру, выражают формулой:
Добротность электрических контуров, которые применяются в радиотехнике, обычно порядка нескольких десятков и даже сотен.
Стоит обратить внимание на то, что собственная частота ω свободных колебаний в контуре с не самой высокой добротностью несколько уступает собственной частоте ω 0 идеального контура с такими же значениями L и C . Однако при Q ≥ ( 5 ÷ 10 ) данным различием можно пренебречь.
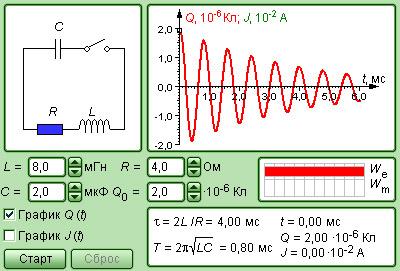
Рисунок 2 . 2 . 4 . Модель свободных колебаний в R L C -контуре.
Видео:Свободные электромагнитные колебания. 11 класс.Скачать

Колебательный контур в физике — формулы и определения с примерами
Колебательный контур:
Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре. Правило Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение внешнего магнитного потока, вызвавшее данный ток.
Рассмотрим электрическую цепь, содержащую конденсатор электроемкостью С и катушку (соленоид) индуктивностью L (рис. 15). Такая цепь называется идеальным колебательным контуром или LC-контуром.
В отличие от реального колебательного контура, который всегда обладает некоторым электрическим сопротивлением (R
Пусть в начальный момент времени (t = 0) конденсатор С заряжен так, что на его первой обкладке находится заряд +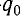

С течением времени конденсатор начнет разряжаться, и в цепи появится электрический ток, сила l(t) которого будет меняться с течением времени. Поскольку при прохождении такого электрического тока в катушке индуктивности возникнет изменяющийся во времени магнитный поток, то это вызовет появление ЭДС самоиндукции, препятствующей изменению силы тока.
Вследствие этого сила тока в колебательном контуре будет возрастать от нуля до максимального значения в течение некоторого промежутка времени, определяемого индуктивностью катушки.
В момент полной разрядки конденсатора (q = 0) сила тока в катушке I(t) достигнет своего максимального значения 
После разрядки конденсатора сила тока в катушке начнет убывать. Это также произойдет не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создаст индукционный ток. Он будет иметь такое же направление, как и уменьшающийся ток в цепи, и поэтому будет «поддерживать» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезарядит конденсатор до начального напряжения обратной полярности — знак заряда на каждой обкладке окажется противоположным начальному.
Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения 
Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.
Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением в катушке ЭДС самоиндукции, которая «обеспечивает» эту перезарядку. Заметим, что заряд q(t) конденсатора и сила тока I(t) в катушке достигают своих максимальных значений 

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Период свободных электромагнитных колебаний в контуре определяется по формуле Томсона:
Получим эту формулу, используя закон сохранения энергии. Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство
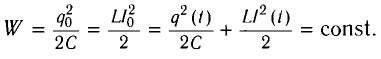
Поскольку закономерности гармонических колебаний носят универсальный характер, то можно сравнить колебания в LC-контуре с колебаниями пружинного маятника.
Для пружинного маятника полная механическая энергия в любой момент времени 2 ,
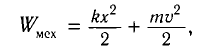
и период его колебаний
Проанализируем соотношения (1) и (2). Сравним выражения для энергии электростатического поля конденсатора 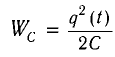
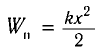
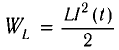
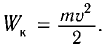
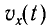
Следуя аналогии, заменим в формуле для периода колебаний пружинного маятника т на L и k на 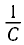
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).
Таблица 4
Сопоставление физических величин, характеризующих электромагнитные и механические колебания
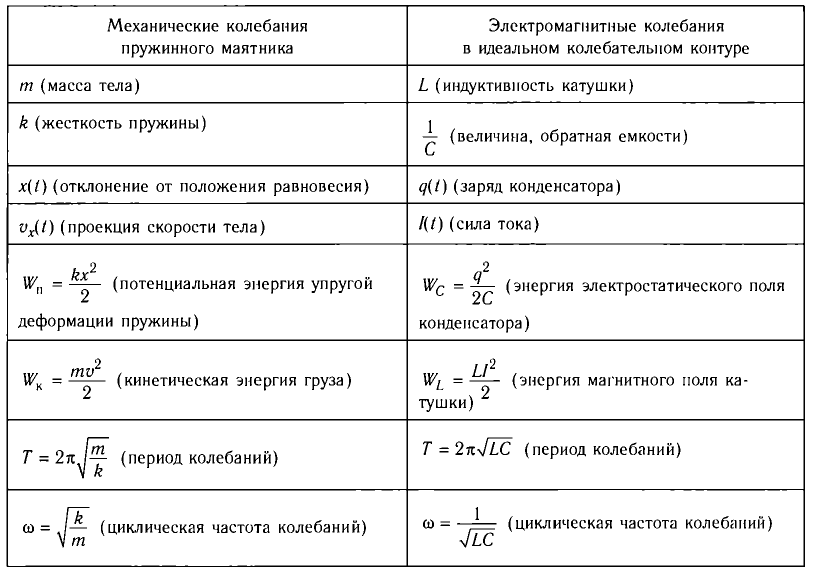
Соответственно, зависимость заряда конденсатора от времени будет иметь такой же характер, как и зависимость координаты (смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону (но с другими начальными фазами) будут изменяться сила тока в цепи, напряжение на конденсаторе.
Для определения начальной фазы 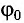
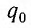
Полная энергия идеального колебательного контура (R = 0) с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется.
Как уже отмечалось, реальный колебательный контур всегда имеет некоторое сопротивление R, обусловленное сопротивлением катушки, соединительных проводов и т. д. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они «будут происходить» сколь угодно долго.
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без трения, а механическим аналогом реального колебательного контура — пружинный маятник с трением.
Пример №1
При изменении емкости конденсатора идеального LC-контура на 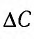
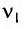
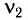
Решение
Частота колебаний в контуре
Поскольку частота колебаний в контуре увеличилась (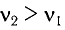
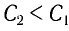
Из условия задачи получаем систему уравнений
Откуда
Вычитая из первого уравнения второе, получаем
Ответ: L = 0,015 Гн.
Пример №2
Колебательный контур состоит из конденсатора емкостью С = 400пФ и катушки индуктивностью L=10 мГн. Определите амплитудное значение силы тока 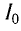
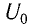
Решение
Максимальная энергия электростатического поля конденсатора
а максимальная энергия магнитного поля катушки
Так как контур идеальный (R = 0), то его полная энергия не меняется с течением времени. Кроме того, в момент, когда заряд конденсатора максимален, сила тока в катушке равна нулю, а в момент, когда заряд конденсатора равен нулю, сила тока в ней максимальна. Это позволяет утверждать, что максимальные энергии в конденсаторе и катушке равны: 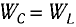
откуда
Ответ: 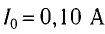
Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Колебательный контур и свободные электромагнитные колебания в контуре
Явление возникновения ЭДС в любом контуре при изменении магнитного потока через поверхность, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в замкнутом проводящем контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.
Правило Ленца: возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором созданный им магнитный поток через поверхность, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.
Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора электроемкостью 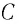
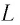
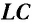
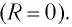
Подключив (при помощи ключа 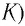
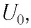
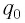
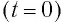
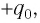
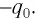
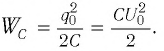
Рассмотрим процесс разрядки конденсатора в колебательном контуре. После соединения заряженного конденсатора с катушкой (при помощи ключа 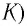
Таким образом, в контуре появится нарастающий по модулю электрический ток, сила 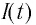
Вследствие этого модуль силы тока в колебательном контуре будет в течение некоторого промежутка времени плавно возрастать от нуля до максимального значения 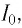
При разрядке конденсатора энергия его электростатического поля превращается в энергию магнитного поля катушки с током. Согласно закону сохранения энергии суммарная энергия идеального колебательного контура остается постоянной с течением времени (уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки):
где 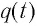
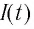
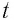
В момент полной разрядки конденсатора 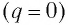
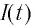
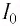
После разрядки конденсатора сила тока в катушке начинает убывать по модулю. Это также происходит не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создает индукционный ток. Он имеет такое же направление, как и уменьшающийся по модулю ток в цепи, и поэтому «поддерживает» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезаряжает конденсатор до начального напряжения 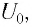
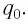
Таким образом, в идеальном 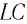
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без пополнения энергии от внешних источников.
Таким образом, существование свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора, вызванной возникновением ЭДС самоиндукции в катушке. Заметим, что заряд 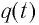
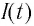
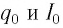
Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальным значениям заряда на каждой из обкладок), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии. Поскольку полная энергия идеального 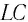
Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:
где 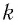
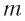
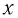
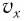
Период его колебаний:
Проанализируем соотношения (1) и (2). Видно, что энергия электростатического поля конденсатора 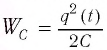
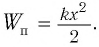
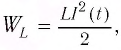
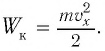
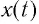
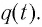
Следуя проведенной аналогии, заменим в формуле для периода колебаний пружинного маятника массу 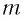
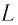
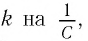
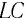
которая называется формулой Томсона.
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).

Зависимость заряда конденсатора от времени имеет такой же вид, как и зависимость координаты (проекции смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону изменяются сила тока (но с другой начальной фазой) в цепи и напряжение на конденсаторе.
Для определения начальной фазы 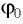
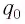
Отметим, что колебательный контур, в котором происходит только обмен энергией между конденсатором и катушкой, называется закрытым.
Полная энергия идеального колебательного контура 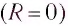
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура — пружинный маятник с учетом трения.
Пример решения задачи:
Идеальный колебательный контур состоит из конденсатора емкостью 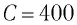
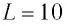
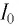
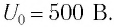
Дано:

Решение
Максимальная энергия электростатического поля конденсатора:
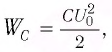
а максимальная энергия магнитного поля катушки:
Так как контур идеальный 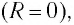
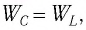
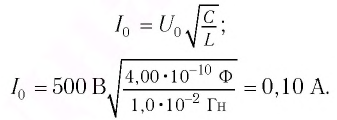
Ответ:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Исследовательские методы в физике
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Распространение механических волн в средах
- Электромагнитное поле
- Опыты Фарадея в физике
- Электромагниты и их применение в физике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📹 Видео
Составление дифференциального уравненияСкачать

1. Что такое дифференциальное уравнение?Скачать

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Классические уравнения | колебательный контур | разбираемся с решениямиСкачать

Колебательный контурСкачать

4. Однородные дифференциальные уравнения (часть 1)Скачать

Однородное дифференциальное уравнениеСкачать

71. Вынужденные колебанияСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Дифференциальные уравнения. 11 класс.Скачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать