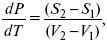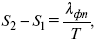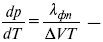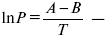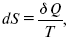Оно позволяет применить второй закон термодинамики к фазовым переходам. Если рассчитать процессы, в которых совершается только работа расширения, то тогда изменение внутренней энергии
Предположим, что 1 моль вещества переходит из первой фазы во вторую.
нет условного равновесия,
где dP/dT – температурный коэффициент давления,
где λфп – теплота фазового перехода.
уравнение Клаузиуса-Клапейрона, дифференциальная форма уравнения.
Уравнение устанавливает взаимосвязь между теплотой фазового перехода, давлением, температурой и изменением молярного объема.
эмпирическая форма уравнения Клаузиуса-Клапейрона.
Уравнение Клаузиуса-Клапейрона изучает фазовые переходы. Фазовые переходы могут быть I рода и II рода.
I рода – характеризуются равенством изобарных потенциалов и скачкообразными изменениями S и V.
II рода – характеризуются равенством изобарных потенциалов, равенством энтропий и равенством молярных объемов.
I рода – ΔG = 0, ΔS ≠ 0, ΔV ≠ 0.
II рода – ΔG = 0, ΔS = 0, ΔV = 0.
Алгебраическая сумма приведенных теплот для любого обратимого кругового процесса равна нулю.
Эта подынтегральная величина – дифференциал однозначной функции состояния. Эта новая функция была введена Клаузиусом в 1865 г. и названа энтропией – S (от греч. «превращение»).
Любая система в различном состоянии имеет вполне определенное и единственное значение энтропии, точно так же, как определенное и единственное значение Р, V, Tи других свойств.
Итак, энтропия выражается уравнением:
где S – это функция состояний, изменение которой dSв обратимом изотермическом процессе перехода теплоты в количество Q равно приведенной теплоте процесса.
При независимых переменных U (внутренняя энергия) может обозначаться UВН и V (объем), или Р (давление) и Н(энтальпия). Энтропия является характеристической функцией. Характеристические функции – функции состояния системы, каждая из которых при использовании ее производных дает возможность выразить в явной форме другие термодинамические свойства системы. Напомним, в химической термодинамике их пять:
1) изобарно-изотермический потенциал (энергия Гиббса) при независимых переменных Т, Р и числе молей каждого из компонентов и.;
2) изохорно-изотермический потенциал (энергия Гельмгольца) при независимых переменных Т, V, ni;
3) внутренняя энергия при независимых переменных: S, V, ni;
4) энтальпия при независимых переменных: S, Р, пi;
5) энтропия при независимых переменных Н, Р, ni..
В изолированных системах (U и V= const) при необратимых процессах энтропия системы возрастает, dS > 0; при обратимых – не изменяется, dS = 0.
Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

ВЫВОД И АНАЛИЗ УРАВНЕНИЯ КЛАПЕЙРОНА – КЛАУЗИУСА.
ТЕПЛОВЫЕ ЭФФЕКТЫ ФАЗОВЫХ ПЕРЕХОДОВ.
УРАВНЕНИЕ КЛАПЕЙРОНА – КЛАУЗИУСА.
Переход компонента из одной фазы в другую сопровождается выделением или поглощением теплоты, которую можно определить количественно на основе фундаментального уравнения термодинамики:

ВЫВОД И АНАЛИЗ УРАВНЕНИЯ КЛАПЕЙРОНА – КЛАУЗИУСА.
Для любого равновесного перехода вещества из одной фазы α в другую фазу β, применяя уравнение (*) к каждой из фаз, можно написать
Индексы α и β отражают принадлежность параметров к соответствующей фазе. В равновесных условиях между фазами α и β изменение энергии Гиббса отсутствует, т.е.


Для равновесного обратимого процесса согласно уравнениям 


а уравнение (3) примет вид

где ∆Hпер – теплота фазового перехода.
Тепловой эффект, сопровождающий фазовый переход, определяется следующим образом:

где ∆V – изменение объема в результате фазового перехода; dP/dT – изменение давления в зависимости от температуры при сохранении равновесия между двумя фазами.
Уравнение Клапейрона–Клаузиуса связывает тепловой эффект процесса с изменением давления насыщенного пара, температурой и изменением объема в процессе фазового перехода.
Для процессов испарения ж→п и сублимации тв→п уравнение Клапейрона–Клаузиуса можно представить следующим образом:
где ∆Hисп , ∆Hсуб – теплоты испарения и сублимации; Vп, Vж, Vтв – мольные объемы пара, жидкости и твердого тела соответственно.
В процессе испарения и сублимации наблюдается значительное изменение удельного объема ∆V и существенное изменение величины dP/dT. При плавлении, напротив, изменение ∆V невелико, и величина dP/dT незначительна.
Пример 1. Проведем расчет по уравнению Клапейрона–Клаузиуса температуры плавления фенола Тпл. Плотность твердого фенола ρтв при атмосферном давлении составляет 1,072∙10 3 кг/м 3 , а жидкого ρж = 1,056∙10 3 кг/м 3 ; теплота плавления ∆Hпл = 1,045∙10 5 Дж/кг; температура замерзания 314,2 К. Определим dP/dT и температуру плавления при Р = 5,065∙10 7 Па:
Прирост температуры плавления при повышении давления на 1 атм ( 1,013∙10 5 Па) составляет 4,525∙10 -8 град/Па. При увеличении давления до 5,065∙10 7 Па температура плавления увеличивается на ∆T = (dT/dP)∆P = 4,525∙10 -8 ∙ 5,065∙10 7 = 2,29 К, т.е. составит Тпл = 314,2+2,29 = 316,49 К.
Следует иметь в виду, что в процессе плавления у большинства веществ Vж > Vтв , тогда ∆V>0 и при повышении давления Р↑ температура плавления повышается Т↑.
Однако, такие вещества как вода (Н2О), висмут (Bi), имеют объем твердой фазы Vтв больше, чем объем жидкой фазы Vж уд = 10 -3 м 3 /кг и Vтв уд = 1,091·10 -3 м 3 /кг; теплота плавления ∆Hпл = 332,4 кДж/кг:
Это значение показывает, что для понижения температуры таяния льда на один градус Кельвина необходимо увеличить давление на 1,34∙10 7 Па, т.е. примерно на 134 атмосферы, что нереально, поскольку такое давление лед не выдерживает – трескается.
Таяние льда происходит в основном в результате трения и превращения работы в теплоту при скольжении конька по льду, а не за счет повышения давления на лед.
Уравнение для процесса испарения 
Пар подчиняется законам идеального газа: PV=RT 


Проведем интегрирование уравнения (1) в пределах от Т1 до Т2 и соответственно от Р1 до Р2 при условии, что в области невысоких давлений пара ∆Нисп ≈ const; в результате интегрирования получим:
∆Нисп / R = const, выносим за знак интеграла
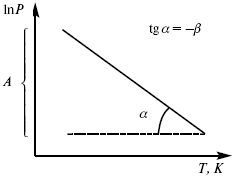
При помощи уравнения (2) можно графически определить значения теплоты испарения, если известны давления Р1 и Р2 и соответствующие им температуры испарения Т1 и Т2 . Для этого необходимо отложить на оси абсцисс значения обратной температуры, а на оси ординат – lnP.
Зависимость lnP от 1/Т будет линейной, а тангенс угла наклона этой прямой равен 

Расчетные значения ∆Нисп получаются с достаточной для практики точностью, не уступающей точности непосредственного измерения. Возможно использование уравнения (2) для обратного расчета, когда по значению ∆Нисп определяют изменение давления при изменении температуры в процессе испарения.
Теплоту фазовых переходов можно определить и по величине стандартной энтальпии образования, в зависимости от фазового состояния продуктов реакции.
Пример. Лучше всего это показать на примере теплоты образования воды из газообразных кислорода и водорода, которая составляет
для водяного пара ∆Н(г) 0 = -241,82 кДж/моль; для воды в жидком состоянии ∆Н(ж) 0 = -285,83 кДж/моль; для льда ∆Н(тв) 0 = -291,82 кДж/моль. Теплота конденсации воды равна:
а теплота превращения воды в лед:
Как видно, тепловой эффект фазовых переходов значительно меньше теплоты образования веществ.
В результате фазовых переходов происходит изменение энтропии. Такие изменения в зависимости от температуры представим на рисунке.
Как известно, энтропия идеального кристалла при абсолютном нуле равна нулю. С ростом температуры атомы (ионы) флуктуировать относительно равновесного положения, число возможных способов их размещения растет, и энтропия увеличивается (ΔS>0). При достижении температуры плавления (точка А на рисунке) кристаллическая решетка разрушается скачкообразно (отрезок АБ), увеличивается термодинамическая вероятность системы W, а в соответствии с формулой S=k∙lnW (где k – постоянная Больцмана) энтропия при переходе от твердого в жидкое состояние растет. Более значительный скачок энтропии имеет место при переходе из жидкого состояния в газообразное (отрезок ВГ), когда ближний порядок расположения частиц друг относительно друга нарушается, и движение частиц становится хаотичным.
Пример. Оценим скачок энтропии на примере фазовых переходов воды:

когда известны стандартные абсолютные значения энтропии Sтв 0 =39,4; Sж 0 =69,9; Sг 0 =188,7 Дж/(моль·К).
В соответствии с рисунком для воды
По известной энтальпии фазового перехода можно рассчитать изменение энтропии в соответствии с формулой
Пример.Вычислим изменение энтропии в процессе парообразования 1 моля этилхлорида при 12,3 0 С, когда теплота испарения ∆Нисп =24,16 кДж/моль.
Молекулярная масса 
В заключение отмечу, что мы рассматривали лишь фазовые переходы I рода. При фазовых переходах I рода свойства веществ, выражаемые, например, через химический потенциал, первыми производными одной из характеристических функций, изменяются скачком при непрерывном изменении соответствующих параметров: температуры, давления, объема и энтропии. При этом выделяется или поглощается теплота перехода ∆Нпер в соответствии с уравнением Клапейрона–Клаузиуса.
Кроме них, однако, существуют фазовые переходы II рода. Они не сопровождаются выделением или поглощением теплоты, для них уравнение Клапейрона–Клаузиуса теряет смысл. Эти переходы характеризуют изменения в системе, которые не определяются объемом и запасом энергии. В этом случае первые производные одной из характеристических функций непрерывны, а вторые производные (например, теплоемкость) изменяются скачком. К фазовым переходам II рода относятся переходы парамагнетика в ферромагнетик, диэлектрика в сегнетоэлектрик, а также процессы возникновения сверхтекучести, сверхпроводимости и др.
В настоящее время насчитывается около 400 твердых минералов, для которых наблюдаются фазовые переходы II рода: рутил, анатаз, алмаз и особенно кварц, который имеет семь модификаций, причем наряду с фазовыми переходами I рода наблюдаются фазовые переходы II рода. Так, при 573 0 С и переходе модификации кварца β 
Видео:Физическая химия # 2. Вывод уравнения Клаузиуса-КлапейронаСкачать

Взаимосвязь свойств и функций состояния индивидуальных веществ при фазовых переходах. Уравнение Клапейрона-Клаузиуса, его дифференциальные и интегральные формы.
Фазовые переходы в таких системах сопровождаются изменением агрегатного состояния. Например, в процессе испарения жидкости устанавливается равновесие жидкость ⇄ пар; равновесие твёрдое тело ⇄ жидкость характеризует процесс плавления/кристаллизации. Особую группу составляют фазовые переходы в твердом теле:твёрдое тело(1)⇄ твёрдое тело(2). Они представляют собой структурные превращения (например, превращение графита в алмаз или структурные переходы в активных материалах, в частности, в сегнето- или антисегнетоэлектриках).
| Равновесия, названия процессов | Знак ΔНпроцесса (λпроцесса) | Знак ΔSпроцесса | Актуальность понимания | |
температурной зависимости равновесного давления паров  | барической зависимости температуры фазового перехода (фазового превращения)  | |||
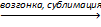 т ⇄ п т ⇄ п  | λвозгонки≫0 | ΔSвозгонки ≫0 | Да, соответствующая зависимость имеет важное значение. Формулу для её анализа нужно получить. | Данная зависимость редко анализируется. |
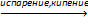 ж ⇄ п ж ⇄ п 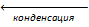 | λкипения >0 | ΔSкипения >0 | Да, соответствующая зависимость имеет важное значение. Формулу для её анализа нужно получить. | Да, соответствующая зависимость имеет важное значение. Формулу для её анализа нужно получить. |
 т ⇄ ж т ⇄ ж  | λплавления ≳0 | ΔS плавления≳0 | Данная зависимость редко анализируется, т.к. в системе отсутствует собственная паровая фаза. | Да, соответствующая зависимость имеет важное значение. Формулу для её анализа нужно получить. |
 т(1) ⇄ т(2) т(1) ⇄ т(2) 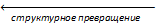 | λструкт.превр.≶0 | ΔSстр.пр. ≶0 | Данная зависимость редко анализируется, т.к. в системе отсутствует собственная паровая фаза. | Да, соответствующая зависимость имеет важное значение. Формулу для её анализа нужно получить. |
Вначале рассмотрим равновесие твёрдое тело ⇄ пар, которое называют процессом возгонки или сублимации. Затем кратко обоснуем вид аналогичных соотношений для других межфазных равновесий.
Пусть мы имеем в состоянии равновесия 1моль твердого вещества и 1моль его пара. Наличие динамического равновесия означает, что мольные изобарно-изотермические потенциалы соответствующих фаз совпадают: Gт = Gп. В предыдущей части лекции, посвященной обоснованию принципа Ле-Шателье, было показано, что увеличением температуры (на произвольную величину dT) и одновременным увеличением давления (на конкретную величину dp) можно добиться одинакового изменения энергии Гиббса обеих фаз (на dG), и перевести систему в новое равновесие. Для него будут равны новые значения изобарных потенциалов:
Поскольку одновременно равны и первые слагаемые, следовательно, можем записать:
Теперь используем связь полного дифференциала энергии Гиббса с ее характеристическими параметрами:
В итоге получаем:
Перегруппируем слагаемые и поделим на dT: Sп — Sт = (Vп — Vт) 
Слева имеем ΔSвозг. = Sп — Sт. По II-му началу термодинамики можем заменить эту разность на приведенную теплоту этого процесса:


Выполняем замену в (V.1)и переносимТвозг в правую часть равенства:
ΔНвозг = Твозг(Vп — Vт) 
Уравнение (V.2) известно как уравнение Клапейрона-Клаузиуса для равновесия твердое тело ⇄ пар. Его можно упростить, принимая во внимание, что Vп ≫ Vт.
Получаем: ΔНвозг ≈ ТвозгVп 


Важно отметить, что в правой части полученного равенства все величины положительны (в том числе и числитель, поскольку возгонка — безусловно эндотермический процесс, требующий затраты энергии на перевод твердого тела в газовую фазу). Таким образом, имеем:

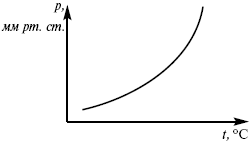
что означает, что при увеличении температуры повышается равновесное давление пара над твердой фазой. Поэтому в р-Т координатах соответствующая межфазная граница должна иметь положительный угловой коэффициент. Кроме того, следует учесть, что такое равновесие следует ожидать при низких температурах (при высоких Т твердая фаза может не сохраниться и, скажем, расплавиться) и низких давлениях (при высоких р газовая фаза может сконденсироваться в жидкость). Таким образом, при охлаждении линия равновесия твёрдое тело ⇄ пар устремляется к началу координат (при Т → 0К рпаров также уменьшается до нуля). В то же время, в направлении высоких температур и давлений эта линия должна быть ограничена точкой, в которой появится вторая конденсированная фаза — жидкость:




В свою очередь, барическая зависимость температуры возгонки описывается обратным соотношением:
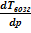

Если давление насыщенных паров невелико, то можно считать, что они (пары) обладают свойствами идеального газа ( 







В небольшом интервале температур можно считать теплоту фазового перехода постоянной величиной. Тогда после интегрирования последнего уравнения получаем:







Соответственно, λвозг может быть найдена через угловой коэффициент прямой, построенной по экспериментальным значениям логарифма равновесного давления паров при разных температурах.
Расчет по второму уравнению менее надежен, поскольку в нем используются только два значения равновесного давления паров и, поэтому, больше вероятность ошибки, вносимой погрешностями эксперимента:

Из УрКл-Кл_1-инт’ можно получить формулу температурной зависимости давления насыщенного пара:




Аналогичными преобразованиями уравнения, связывающего полный дифференциал энергии Гиббса с ее характеристическими параметрами, можно получить очень похожие выражения для уравнения Клапейрона-Клаузиуса применительно к равновесию жидкость ⇄ пар. Дополнительная особенность состоит лишь в том, что в дифференциальном виде для данного равновесия интерес представляет не только температурная зависимость давления насыщенного пара над жидкостью ( 
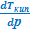
ΔНисп ≈ ТиспVп 



При выводе этих формул было использовано условие Vп ≫ Vт. После замены 

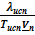
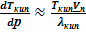
Линия равновесия жидкость ⇄ пар на фазовой p-T-диаграмме начинается из точки В
(см. рис.5.3), которая, как показано ранее, соответствует максимальной температуре, при которой еще сохраняется равновесие твёрдое тело ⇄ пар. Поскольку в выражении УрКл-Кл_2-диф 
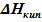


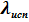
· 


· для равновесия ж⇄п угловой коэффициент равен 


Еще одной важной особенностью кривой равновесия жидкость ⇄ пар является то, что она обрывается в точке К, которая соответствует критическому состоянию вещества. Наличие такой точки на линии равновесия жидкость ⇄ пар является отражением того факта, что структура этих фаз не отличается принципиально. В жидкой фазе структурные единицы (молекулы, ионы или атомы) менее подвижны, лучше связаны, чем в газовой. Но в обеих фазах отсутствует дальний порядок, расположение частиц в целом хаотично. При нагревании растет внутренняя энергия, хаотичность в распределении частиц (энтропия). При этом различие между жидкостью и паровой фазой уменьшаются. В итоге при критических условиях (ркрит, Ткрит) обе фазы оказываются тождественными: становится одинаковой плотность, а значит и мольные объемы, а, следовательно, и энтропии «жидкости» и «пара«. Равенство мольных объемов и энтропий равновесных фаз означает, что при выводе уравнения Клапейрона-Клаузиуса в выражении Sп — Sж = (Vп — Vж) 
Описание равновесия твёрдое тело ⇄ жидкость начнем с кратких комментариев к положению соответствующей межфазной границы на диаграмме состояния.
· Не будем тратить много времени на строгое доказательство, что она должна выходить из точки пересечения линий равновесий твёрдое тело ⇄ пар и жидкость ⇄ пар.
· При выводе уравнения Клапейрона-Клаузиуса покажем, что угловой коэффициент линии равновесия твёрдое тело ⇄ жидкость может иметь разный знак, но практически всегда она располагается практически вертикально.
· Третье важное соображение основано на принципиальных отличиях твердых кристаллических фаз от жидкостей. Поэтому физические свойства данных фаз, их термодинамические характеристики при любых условиях будут существенно отличаться, следовательно, соответствующая межфазная граница не должна обрываться. Особые критические состояния вещества на этой границе не обнаруживаются.
Пусть мы имеем в состоянии равновесия 1моль твердого вещества и 1моль жидкости. Состояние равновесия означает, что Gт = Gж. Увеличением температуры (на произвольную величину dT) и одновременным увеличением давления (на конкретную величину dp) переведем систему в новое равновесие:
Учитывая, что энергия Гиббса является характеристической функцией от давления и температуры, получаем:
После перегруппировки имеем: (Sж — Sт) 
Обращаю внимание, что в данном случае интерес представляет именно влияние давления на температуру плавления, т.е. 
Слева имеем ΔSпл = Sж — Sт. По II-му началу термодинамики можем заменить эту разность на приведенную теплоту этого процесса: 

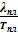
После подстановки в (V.3)и небольшого преобразования можем получить выражения для оценки теплоты плавления и, что более важно, для анализа барической зависимости температуры плавления:
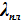

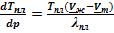
Дальнейшее преобразование, упрощение полученных равенств невозможно, поскольку молярные объемы твердой и жидкой фаз сопоставимы. Это означает, что Vж — Vт ≈ 0, следовательно, 
р—T-диаграмме практические вертикально. Что касается ее наклона, то знак 




Для равновесия твёрдое тело(1)⇄ твёрдое тело(2) вывод и полнота преобразования уравнения Клапейрона-Клаузиуса полностью аналогична только что разобранному случаю. Приведу только окончательное выражение в дифференциальной форме:

Но в отличие от формулы (УрКл-Кл_3-диф) в данном случае ситуация еще более неопределенная, поскольку нельзя заранее предсказать не только знак разности 
📽️ Видео
Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

Успеть за 300 секунд, #3: Уравнение Клапейрона-МенделееваСкачать

Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Коробов М. В. - Физическая химия. Часть 1 - Основные понятия, свойства системыСкачать
Уравнение состояния идеального газа. 10 класс.Скачать

Решить задачу Коши для дифференциального уравнения с помощью формулы ДюамеляСкачать

Коробов М. В. - Физическая химия. Часть 1 - Химический потенциалСкачать

Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

ФИЗИЧЕСКАЯ ХИМИЯ (ТЕРМОДИНАМИКА). ОСНОВНЫЕ ПОНЯТИЯ: СИСТЕМЫ, ПАРАМЕТРЫ, ФУНКЦИИСкачать

Вывод уравнения неразрывности - Лекция 1Скачать

Физическая химия, 2 лекция, Траньков С. В., 08.09.2022, 2 курсСкачать

№9. Элементы вариационного исчисления. Уравнения Лагранжа-Эйлера.Скачать

11. Уравнения в полных дифференциалахСкачать

Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать

Приведение линейного уравнения в частных производных c постоянными коэфф--ми к каноническому виду.Скачать

Физическая химия. Лекция 1. Химическая термодинамикаСкачать

Уравнение Мещерского и формула Циолковского LIVE | 11 класс, студенты МФТИ | Вузовская физика с FСкачать