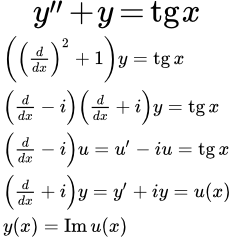Диф уравнения второго порядка с комплексными числами

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Решения неоднородных дифференциальных уравнений 2-го порядка с постоянными коэффициентами. Комплексные числа

по высшей математике

Решения неоднородных дифференциальных уравнений 2-го порядка с постоянными коэффициентами. Комплексные числа

Студентка II курса

I. у″ — 4y′ + 4y = соs4х

у = U + у(_) — общ. реш. н. д. у.

2) у(_) =? у(_) = Acos4x + Bsin4xy(_)′ = — 4Asin4x + 4Bcos4x

y″ = — 16Acos4x — 16Bsin4x

16Acos4x — 16Bsin4x + 16Asin4x + 16Bcos4x + 4Acos4x +4Bsin4x =

= cos4x + 0 ∙ sin4x

12Acos4x — 12Bsin4x + 16Asin4x + 16Bcos4x = cos4x + 0 ∙ sin4x

12A + 16A = 016B — 12B = 0

y(_) = 4cos4x + 4sin4x

y = C₁e 2x + C₂e 2x · x + 4cos4x + 4sin4x — общее решение н. д. у.

Найдем частное решение при условии:

у′ = 2С₁e 2 x + 2C₂e 2 x · x — 16sin4x + 16cos4x

у = — 10е 2х + 13е 2х · x + 4cos4x + 4sin4x — частное решение при заданных условиях

II. у″ — 4y′ + 4y = 5х 2 + 3х + 1

у = U + у(_) — общее решение н. д. у.

2) у(_) =? у(_) = Ах 2 + Вх + Сy(_)′ = 2Ах + В

2А — 8В + 4В + 4Ах + 4Вх + 4С = 5х 2 + 3х + 1

4А = 5А = 5/4 В = 3 С = 1/4

у(_) = 5/4х 2 + 3 + 1/4

у = C₁e 2 x + С₂е 2х ∙ х + 5/4х 2 + 3 + 1/4 — общее решение н. д. у.

Найдем частное решение при условии:

у′ = 2С₁e 2 x + 2C₂e 2 x + 5/2х — 1/8

у = — 2e 2 x + 9/4е 2х ∙ х + 5/4х 2 + 3 + 1/4 — частное решение при заданных условиях.

III. у″ — 4у′ + 4у = 2е 5х

у = U + у(_) — общее решение н. д. у.

2) у(_) =? у(_) = Ае 5х y(_)′ = 5А 5х

25Ае 5х — 20Ае 5х + 4А 5х = 2е 5х

А = 2/9 у(_) = 2/9е 5х

у = C₁e 2 x + С₂е 2х ∙ х + 2/9е 5х — общее решение н. д. у.

Найдем частное решение при условии:

у′ = 2C₁e 2 x + 2С₂е 2х ∙ х + 10/9е 5х

у = 4/9e 2 x + 1/3е 2х ∙ х + 2/9е 5х — частное решение при заданных условиях.

Ö — 1 = i — мнимое число

(Ö — 1) 2 = i 2 i 2 = — 1

i 3 = i 2 ∙ i = — 1 ∙ i = — i

i 4 = i 2 ∙ i 2 = ( — 1) ∙ ( — 1) = 1

а + вi — комплексные числа, где: а, в — действительные числа или а, в є R

Геометрический смысл комплексного числа:

в

. (а; в)

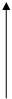
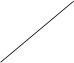
ρ в ρ = Ö а 2 + в 2 = çа + вiú

) d а

аргумент комплексного числа

(находится с учетом четверти)

tg

нет

0 0

cosd = a / ρ a = ρcosd

sind = в / ρ в = ρsind

а + вi = ρcosd + i ρsind

а + вi = ρ (cosd + i sind) –

комплексное число в тригонометрической форме

Действия с комплексными числами:

Формула Эйлера: Комплексное число в показательной форме:

е i у = cosу + isinу z = ρе i φ

Примеры по возведению комплексного числа в степень в тригонометрической и показательной формах:

1) (7 + 3i) (3 + 7i) = 21 + 21i 2 + 9i + 49i = 58i

(7 + 3i) = Ö 58 (cosarctg 3/ 7 + isinarctg 3/ 7) = е ln Ö 58 × е arctg 3/7 = е ln Ö 58 + i arctg 3/7

(3 + 7i) = Ö 58 (cosarctg 7/ 3 + isinarctg 7/ 3) = е ln Ö 58 × е arctg 7/ 3 = е ln Ö 58 + i arctg 7/ 3

Ö 58 (cosarctg 3/ 7 + isinarctg 3/ 7) Ö 58 (cosarctg 7/ 3 + isinarctg 7/ 3) =

= 58 (cos (arctg 3/ 7 + arctg 7/ 3) + i (sin (arctg 3/ 7 + arctg 7/ 3))) =

= е ln 58 × е i (arctg 3/ 7 + arctg 7/ 3) = е ln 58 + i (arctg 3/ 7 + arctg 7/ 3)

При решении примера использовали формулу:

е ln 58 + i (arctg 3/ 7 + arctg 7/ 3) = е ln 58 × е i (arctg 3/ 7 + arctg 7/ 3) =58 (cos (arctg 3/ 7 + arctg 7/ 3) + i (sin (arctg 3/ 7 + arctg 7/ 3)

cos (arctg 3/ 7 + arctg 7/ 3) = cos (arctg 3/ 7) cos (arctg 7/ 3) —

sin (arctg 3/ 7) sin (arctg 7/ 3)

cos (arctg 3/ 7) = 1/ (Ö 1 + tg 2 (arctg 3/ 7)) = 1/ Ö 1 + (9/49) = 7/Ö 58

cos (arctg 7/ 3) = 3/Ö 58

sin (arctg 3/ 7) = Ö 1 — cos 2 arctg 3/ 7 = Ö 1 — (7/Ö 58) 2 = Ö 9/ 58 = 3/Ö 58 sin (arctg 7/3) = Ö 1 — cos 2 arctg 7/ 3 = 7/Ö 58

cos (arctg 3/ 7 — arctg 7/ 3) = 7/Ö 58 × 3/Ö 58 — 3/Ö 58 × 7/Ö 58 = 0

sin (arctg 3/ 7 — arctg 7/ 3) = 3/Ö 58× 3/Ö 58 × 3/Ö 58× 3/Ö 58 = 0

Возведение в степень:

(7 + 3i) (3 + 7i) = Ö 58 (cosarctg 3/7 + isinarctg 3/7) = е ln Ö 58 + i arctg 3/7

(7 + 3i) 2 = 49 + 42i + 9i 2 = 40 + 42i

(Ö 58 (cosarctg 3/7 + isinarctg 3/7)) 2 = 58 (cos2arctg 3/7 + isin2arctg 3/7) =

= е ln Ö 58 + i arctg 3/7

е ln Ö 58 + i arctg 3/7 = 58 (cos2arctg 3/7 + isin2arctg 3/7)

cos2arctg 3/ 7 = 2cos 2 arctg 3/7 — 1 = 2 × (7/Ö 58) 2 — 1 = 40/58

sin2arctg 3/ 7 = 2sin 2 arctg 3/ 7 cosarctg 3/ 7 = 2 ∙ (3/Ö 58) ∙ (7/Ö 58) = 42/58

58 (40/58 + 42/58 × i) = 40 + 42i

При решении примера применяли следующие формулы:

(ρ (cosd + i sind)) п = ρ п (cosпd + i sinпd) п є N

е х + iу = е х (cosу + isinу)

2) (3 + 4i) (4 + 3i) = 12 + 12i 2 + 16i + 9i = 25i

(3 + 4i) = 5 (cosarctg 4/ 3 + isinarctg 4/ 3) = е ln 5 × е arctg 4/ 3 = е ln 5 + i arctg 4/ 3

(4 + 3i) = 5 (cosarctg 3/ 4 + isinarctg 3/ 4) = е ln 5 × е arctg 3/ 4 = е ln 5 + i arctg 3/ 4

5 (cosarctg 4/ 3 + isinarctg 4/ 3) 5 (cosarctg 3/ 4 + isinarctg 3/ 4) =

= 25 (cos (arctg 4/ 3 + arctg 3/ 4) + i (sin (arctg 4/ 3 + arctg 3/ 4))) =

= е ln 25 × е i (arctg 4/ 3 + arctg 3/ 4) = е ln 25 + i (arctg 4/ 3 + arctg 3/ 4)

При решении примера использовали формулу:

е ln 25 + i (arctg 4/ 3 + arctg 3/ 4) = е ln 25 × е i (arctg 4/ 3 + arctg 3/ 4) =25 (cos (arctg 4/ 3 +

+ arctg 3/ 4) + i (sin (arctg 4/ 3 + arctg 3/ 4)))

cos (arctg 4/ 3 + arctg 3/ 4) = cos (arctg 4/ 3) cos (arctg 3/ 4) —

sin (arctg 4/ 3) sin (arctg 3/ 4)

cos (arctg 4/ 3) = 1/ (Ö 1 + tg 2 (arctg 4/ 3)) = 1/ Ö 1 + (16/ 9) = 3/ 5

cos (arctg 3/ 4) = 4/ 5

sin (arctg 4/ 3) = Ö 1 — cos 2 arctg 4/ 3 = Ö 1 — 9/ 5 = 4/5

sin (arctg 3/ 4) = Ö 1 — cos 2 arctg 3/ 4 = 3/ 5

cos (arctg 4/ 3 — arctg 3/ 4) = 3/ 5 × 4/5 — 3/ 5 × 4/5 = 0

sin (arctg 4/ 3 — arctg 3/ 4) = 4/ 5 × 3/5 — 4/ 5 × 3/5 = 0

Извлечение корня третий степени из комплексного числа:

п Ö ρ (cosd + i sind) = п Ö ρ (cos d + 2Пк / п + i sin d + 2Пк / п) к є (0; 1;. ; п — 1)

3 Ö 3 +4i = 3 Ö 25 (cosarctg 4/3 + 2Пк/3 +isinarctg 4/3 + 2Пк/3)

z₁ = 6 Ö 25 (cosarctg (4/3) / 3 + isinarctg (4/3) / 3) к = 0

z₂ = 6 Ö 25 (cosarctg (4/3 + 2П) / 3 + isinarctg (4/3 + 2П) / 3) к = 1

z₃ = 6 Ö 25 (cosarctg (4/3 + 4П) / 3 + isinarctg (4/3 + 4П) / 3) к = 2

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Математический портал

Видео:15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Дифференциальные уравнения
• Высшая математика.
• Комплексные числа

Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Комплексные числа

Видео:19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Действия над комплексными числами.

Комплексные числа — числа вида $x+iy,$ где $x,yin mathbb$ а
$,i,$ такое число, что $ i^2=-1.$ Множество комплексных чисел
обозначается $mathbb.$

Видео:18. Линейные неоднородные дифференциальные уравнения 2 порядка с постоянными коэффициентами. часть 3Скачать

Действия над комплексными числами.

Видео:Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

Сложение комплексных чисел:

Видео:Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Умножение двух комплексных чисел:

Видео:17. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами Ч2Скачать

Умножение комплексного числа на действительное:

$$lambda(x+iy)=lambda x+ilambda y.$$

Видео:Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Деление комплексных чисел:

Действительные числа $x$ и $y$ комплексного числа $z=x+iy,$ называются действительной и мнимой частью числа $z$ и обозначаются, соответственно, $Re z=x$ и $Im z=y.$

Два комплексных числа $z_1=x_1+iy_1$ и $z_2=x_2+iy_2$ называются равными в том и только том случае, если $x_1=x_2,$ $y_1=y_2.$

Запись $z=x+iy$ называют алгебраической формой комплексного числа $z.$

Числа $z_1=x+iy$ и $z_2=x-iy$ называют сопряженными.

Примеры:

Выполнить действия над комплексными числами, представив результат в алгебраичекой форме:

1.421. $(2+3i)(3-i).$

Решение:

Ответ: $9+7i.$

1.424. $(2i-i^2)^2+(1-3i)^3.$

Решение.

Ответ: $24+22i.$

Решение.

Ответ: $frac-fraci.$

Решение.

Ответ: $fraci.$

Найти действительные решения следующего уравнения:

1. 430. $(1+i)x+(-2+5i)y=-4+17i.$

Решение.

Ответ: $x=2; y=3.$

Домашнее задание.

Выполнить действия над комплексными числами, представив результат в алгебраичекой форме:

1.422. $(1+2i)^2.$

Ответ: $-3+4i.$

1.423. $(1-i)^3-(1+i)^3.$

1.427. $left(fracright)^3.$

Найти действительные решения следующего уравнения:

1.431. $12((2x+i)(1+i)+(x+y)(3-2i))=17+6i.$

Решить следующие системы линейных уравнений:

1.432. $(3-i)z_1+(4+2i)z_2=1+3i;$

$(4+2i)z_1-(2+3i)z_2=7.$

1.433. $(2+i)z_1+(2-i)z_2=6;$

$(3+2i)z_1+(3-2i)z_2=8.$

Видео:Математика это не ИсламСкачать

Геометрическая интерпретация комплексных чисел.

Множество действительных чисел можно рассматривать как подмножество комплексных чисел, у которых $Im z = 0.$

Можно также изображать комплексное число в виде радиус-вектора $$ и определять его, задавая его длину $r$ и угол $varphi$ между осью $Ox$ и вектором.

Длина этого вектора называется модулем комплексного числа $$|z|=r=sqrtgeq 0,$$ а угол $varphi$ называется аргументом комплексного числа и обозначается $Arg z.$ Аргумент определяется с точностью до слагаемого $2pi k,,,,, (k=0, pm 1, pm 2, pm 3, . )$ и для положительных значений отсчитывается от оси $Ox$ до вектора против часовой стрелки, а для отрицательных значений – по часовой стрелке.

Значение аргумента, который принадлежит интервалу $(-pi, pi],$ называется главным значением аргумента и определяется $arg z.$ Главное значение аргументу числа $x+iy$ можно вычислять по формуле $varphi= arg z=arctgleft(fracright)+kpi,$ где $k=0,$ если $z$ находится в первой или четвертой четвертях, $k=1,$ если $z$ находится во второй четверти, $k=-1,$ если $z$ находится в третей четверти. Если $x=Rez=0,$ то $varphi=pi/2,$ когда $y=Imz>0$ и $varphi=-pi/2,$ когда $y=Imz плоскость называется комплексной плоскостью C (рисунок 1), ось $Ox$ называется действительной осью, а ось $Oy$ – мнимой осью. Таким образом, действительному числу $z=x+0i=x$ отвечает точка на действительной оси, а мнимому числу $z=0+iy=y -$ точка на мнимой оси.

Видео:Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Формулы Эйлера и Муавра. Корень n-й степени с комплексного числа.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Видео:14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Формулы Эйлера:

Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Формула Муавра:

Если $z=re^, $ то $$z^n=r^ne^,$$ или, в тригонометричской форме:

$$z^n=r^n(cos nvarphi+isin nvarphi).$$

Пусть $a=re^, ,, aneq 0,-$ фиксированное комплексное число. Тогда уравнение $z^n=a,,,, nin N,$ имеет в точности $n$ различных решений $z_0, z_1, . z_$ причем эти решения даются формулой $$z_k=sqrt[n]e^<ileft(frac+frackright)>=sqrt[n]left(cosfrac+isinfracright),$$ $$k=0, 1, . , n-1.$$ (здесь $sqrt r$ действительное положительное число) Числа $z_k, ,, k=0, 1, . n-1,$ называются корнями $n-$й степени из комплексного числа $a$ и обозначаются символом $sqrt[n].$

Примеры:

1.483. Доказать формулу Эйлера $cosvarphi=frac<e^+e^>.$

Решение.

Известно, что $e^=cos+isinvarphi.$ Соответственно, $e^=cos+isin(-varphi)=cosvarphi-isinvarphi.$

Отсюда находим $e^+e^=cosvarphi+isinvarphi+cosvarphi-isinvarphi=2cosvarphi.$

Cледовательно, $cosvarphi=frac<e^+e^>.$ Что и требовалось доказать.

Используя формулу Муавра, вычислить следующие выражения:

1.485. $(1+i)^.$

Решение.

Запишем число $z=1+i$ в показательной форме:

Поскольку число $z$ находится в первой четверти, то

Таким образом, мы можем записать число $z=1+i$ в показательной форме: $z=sqrt 2 e^<ifrac>.$

Теперь, используя формулу Муавра можно найти $z^:$

Ответ: $(1+i)^=32i.$

1.491. Используя формулу Муавра, выразить через $cosvarphi$ и $sinvarphi$ функцию$cos 3varphi.$

Решение.

$$+left.cos^3(-varphi)-3icos^2(-varphi)sin(-varphi)+3i^2cos(-varphi)sin^2(-varphi)-i^3sin^3(-varphi)right)=$$ $$=fracleft(cos^3+3i(1-sin^2varphi)sinvarphi-3cosvarphi(1-cos^2varphi)right.-isin^3varphi+$$ $$+left.cos^3varphi+3i(1-sin^2varphi)sinvarphi-3cosvarphi(1-cos^2varphi)-isin^3varphiright)=$$ $$=cos^3varphi+3isinvarphi-3isin^3varphi-3cosvarphi+3cos^3varphi-isin^3varphi=$$ $$=4cos^3varphi-3cosvarphi+3isinvarphi-4isin^3varphi.$$

Ответ: $4cos^3varphi-3cosvarphi+3isinvarphi-4isin^3varphi.$

1.495. Найти и изобразить на комплексной плоскости все корни 2-й, 3-й и 4-й степени из единицы.

Решение.

Запишем число 1 в показательной форме:

$1=1e^.$ То есть $r=1, varphi=0.$

Далее, пользуясь формулой Муавра вычисляем корень второй степени из единицы:

Вычисляем корень третьей степени из единицы:

Вычисляем корень четвертой степени из единицы:

Ответ: Корни второй степени: $z_0=1;,, z_1 =-1.$ Корни третьей сепени: $z_0=1;,, z_1=-frac+ifrac;,, z_2=-frac-ifrac.$ Корни четвертой степени: $z_0=1;,, z_1=i;,, z_2=-1;,, z_3=-i.$

Найти все значения корней:

Решение.

Запишем число $z=-1+isqrt 3$ в показательной форме:

Поскольку число $z$ находится во второй четверти, то

Таким образом, мы можем записать число $z=-1+isqrt 3$ в показательной форме: $z=2 e^<ifrac>.$

Пользуясь формулой Муавра вычисляем корень второй степени из единицы:

Ответ: $pmfrac(1+isqrt 3)$

1.501. $sqrt [5].$

Решение.

Запишем число $z=-1-i 3$ в показательной форме:

Поскольку число $z$ находится в третьей четверти, то

Таким образом, мы можем записать число $z=-1-i$ в показательной форме: $z=sqrt 2 e^<ifrac>.$

Пользуясь формулой Муавра вычисляем корень второй степени из единицы:

1.483. Доказать формулу Эйлера $sinvarphi=frac<e^-e^>.$

Используя формулу Муавра, вычислить следующие выражения:

Используя формулу Муавра, выразить через $cosvarphi$ и $sinvarphi$ следующие функции:

Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Пример комплексной подстановки при решении линейного неоднородного дифференциального уравнения

Видео:Математика без Ху!ни. Линейные неоднородные дифференциальные уравнения 2 порядка.Скачать

Метод понижения порядка линейного неоднородного дифференциального уравнения с комплексными корнями характеристического уравнения

Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами n-го порядка:
(1) .
Мы полагаем, что коэффициенты этого уравнения являются действительными числами. Здесь мы рассматриваем случай, когда характеристическое уравнение
(2)
имеет комплексные корни.

Для решения уравнения (1), применим метод понижения порядка. Поскольку коэффициенты характеристического уравнения (2) являются действительными числами, то его комплексные корни являются попарно комплексно сопряженными. Пусть – два комплексно сопряженные корня: . Запишем исходное уравнение (1) в следующем виде:
(3) ,
где – оператор дифференцирования.

Обозначим:
.
Тогда уравнение (3) принимает следующий вид:
.
Сделаем подстановку:
(4) .
Получаем уравнение первого порядка с комплексным коэффициентом :
.
Или
(5) .
Решение этого уравнения имеет следующий вид (см. страницу метод понижения порядка ):
,
где – комплексная постоянная.

Далее замечаем, что поскольку исходное уравнение (1) имеет действительные коэффициенты, то переменная u и ее производная u′ должны быть действительными. Выразим комплексный корень через действительную и мнимую части:
.
Подставим в (4):
.
Извлекая мнимую часть, получаем:
.
Отсюда
.

Таким образом, в случае с комплексными корнями, один этап решения приводит к понижению порядка на две единицы.

Пример решения дифференциального уравнения

Решить уравнение
(П1) .

Перепишем уравнение в следующем виде:
.
Вводим обозначение :
.

Характеристическое уравнение

имеет комплексные корни: . Тогда
.

Переписываем исходное уравнение:
;
.
Делаем подстановку:
;
(П2) .
Тогда уравнение принимает вид:
;
(П3) .

Это линейное неоднородное дифференциальное уравнение первого порядка. Ищем решение с помощью интегрирующего множителя. Умножим на и выполняем преобразования:
;
;
(П4) ,
где – комплексная постоянная; – действительные постоянные.

Вычисляем интеграл в (П4) с помощью подстановки .

.

Выразим арктангенс через логарифм, используя уравнение: .
;
.
Отсюда
(П5) .

Теперь в правой части (П6) нам нужно отделить вещественную и мнимую части. Мнимая часть уравнения (П6) и даст искомое решение y .

Для преобразования логарифма, используем формулу: . Далее замечаем, что . Тогда при имеем:
.
При :
.
Оба случая можно записать одной формулой:
,
где при нужно взять верхний знак ′+′; при – нижний знак ′–′.

Подставим в (П6) и выполним преобразования:
;
.
Переобозначим постоянную :
(П7) .

Теперь преобразуем экспоненту с помощью формулы Эйлера: , и выразим комплексную постоянную через действительную и мнимую части: . Подставляем в (П7):
.
Выполняем преобразования:

.
Тогда

.
Отделяем мнимую часть:

.

Автор: Олег Одинцов . Опубликовано: 20-07-2013 Изменено: 26-08-2020