Дидактический материал по теме решение квадратных уравнений о мартынова 2001 год (3 видео)

Дидактический материал по математике. «Квадратные уравнения».

Представлено 48 различных карточек, каждая из которых содержит 8 квадратных уравнений всех видов (неполные, приведенные и общего вида). В каждом варианте одно из уравнений не имеет действительных корней, а другое уравнение имеет целочисленные корни.

Все задания всех вариантов снабжены ответами.

Формирование и решение всех заданий выполнено на компьютере по оригинальным программам.

Разработка является частью дипломной работы

Целевая аудитория: для 8 класса

Автор: Ермолина Екатерина Сергеевна
Место работы: РГПУ имени А.И. Герцена
Добавил: ЕСА_1954

Физкультминутки обеспечивают кратковременный отдых детей на уроке, а также способствуют переключению внимания с одного вида деятельности на другой.

Уважаемые коллеги! Добавьте свою презентацию на Учительский портал и получите бесплатное свидетельство о публикации методического материала в международном СМИ.

Диплом и справка о публикации каждому участнику!

© 2007 — 2022 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель: Никитенко Евгений Игоревич

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

Фотографии предоставлены

Содержание

Дидактический материал «Квадратные уравнения»
Просмотр содержимого документа «Дидактический материал «Квадратные уравнения»»
Дидактические материалы по теме Квадратные уравнения методическая разработка (алгебра, 8 класс) по теме
Скачать:
Предварительный просмотр:
💥 Видео

Видео:Как решать квадратные уравнения для чайниковСкачать

Дидактический материал «Квадратные уравнения»

набор дидактического материала при закрпелении решения квадратных уравнений

Просмотр содержимого документа
«Дидактический материал «Квадратные уравнения»»

Дидактический материал по теме

1. Решите квадратное уравнение, разлагая его левую часть на множители:

а) х 2 – х = 0; е) х 2 – 4х + 4 = 0;

б) х 2 + 2х = 0; ж) х 2 + 6х + 9 = 0;

в) 3 х 2 – 3х = 0; з) х 2 + 4х +3 = 0;

г) х 2 – 81 = 0; и) х 2 + 2х – 3 = 0.

д) 4 х 2 – 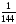= 0;

2. Решите уравнения по формуле:

а) 2х 2 – 5х + 2= 0 г) 4х 2 – 12х +9 = 0

б) 6х 2 + 5х + 1=0 д) 10х 2 – 6х + 0,9 = 0

в) 3х 2 – 7х – 1 = 0 е) 2х 2 – 3х + 2 = 0

3. Не решая квадратного уравнения, определите знаки его корня:

1) х 2 – 2х – 15 = 0 7) х 2 – 2х + 1 = 0

2) х 2 + 2х – 8 = 0 8) х 2 + 4х + 4 = 0

3) х 2 + 10х + 9 = 0 9) х 2 – 6х + 9 = 0

4) х 2 – 12х + 35 = 0 10) 4х 2 + 7х – 2 = 0

5)3 х 2 +1 4х + 16 = 0 11) 5х 2 – 9х – 2 = 0

6) х 2 – 5х + 6 = 0 12) х 2 – 11х + 15 = 0

4. Решите уравнения, используя метод «переброски»:

2х 2 – 9х +9 = 0 5) 3х 2 + х – 4 = 0

10х 2 – 11х + 3 = 0 6) 5х 2 – 11х + 6 = 0

3х 2 +11х +6 = 0 7) 2х 2 + х – 10 = 0

4х 2 +12х + 5 = 0 8) 6х 2 +5х – 6 = 0

5. Решите уравнения, используя свойства коэффициентов:

5х 2 – 7х + 2 = 0 5) 839х 2 – 448х – 391 = 0

3х 2 + 5х – 8 = 0 6) 939х 2 + 978х +39 = 0

11х 2 + 25х – 36 = 0 7) 313х 2 + 326х + 13 = 0

11х 2 + 27х +16 = 0 8) 2006х 2 – 2007х + 1 = 0

6. Решите уравнения по формуле четного коэффициента:

4х 2 – 36х + 77 = 0 3) 4х 2 + 20х + 25 = 0

15х 2 – 22х – 37 = 0 4) 9х 2 – 12х + 4 = 0

7. Решите приведенные квадратные уравнения по формуле:

х 2 – 8х – 9 = 0 3) х 2 + 18х + 81 = 0

х 2 + 6х – 40 = 0 4) х 2 — 56х + 64 = 0

8. Решите графически уравнения:

1) х 2 – х – 6 = 0; 4) х 2 – 2х – 3 = 0;

2) х 2 – 4х + 4 = 0; 5) х 2 + 2х – 3 = 0;

3) х 2 + 4х +6 = 0; 6) 4х 2 – 4х – 1 = 0.

9. Решите с помощью циркуля и линейки следующие уравнения:

1) х 2 – 3х + 2 = 0; 4) 2х 2 – 7х + 5 = 0;

2) х 2 – 3х – 10 = 0; 5) х 2 – 6х + 9 = 0;

3) х 2 +4х + 3 = 0; 6) х 2 +4х + 5 = 0.

10. Решите с помощью номограммы уравнения:

1) z 2 – 7z + 6 = 0; 4) z 2 – z – 6 = 0 ;

2) z 2 + 5z + 4 = 0; 5) z 2 – 11z + 18 = 0;

Видео:РАЗБИРАЕМ ДИСКРИМИНАНТ ЧАСТЬ I #shorts #математика #егэ #огэ #дискриминантСкачать

Дидактические материалы по теме Квадратные уравнения
методическая разработка (алгебра, 8 класс) по теме

Представленные вашему вниманию дидактические материалы предназначены для организации самостоятельной работы учащихся и для осуществления контроля знаний, умений и навыков. Они могут быть использованы как в том случае, когда преподавание ведётся по учебнику «Алгебра, 8» авторов Ю. Н. Макарычева и др., под редакцией С. А. Теляковского, так и тогда, когда преподавание ведётся по другим учебникам. Самостоятельные работы делятся на четыре группы: 1) самостоятельные работы по образцу, т. е. простейшая воспроизводящая самостоятельная работа;

2) реконструктивно-вариатнвная самостоятельная работа; 3) частично – поисковая самостоятельная работа; 4) творческая, исследовательская самостоятельная работа.

Эти дидактические материалы были разработаны тогда, когда я работала над проблемой «Разработка систем разноуровневых заданий для организации самостоятельной работы учащихся 8 класса по теме «Квадратные уравнения».

Видео:Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

Скачать:

Вложение	Размер
didakticheskie_materialy_po_teme_kvadratnye_uravneniya.zip	61.79 КБ

Видео:Решение квадратных уравненийСкачать

Предварительный просмотр:

Бакеева И. Р. МОУ «Бриентская средняя общеобразовательная школа» Кваркенский район.

Важнейшим условием и средством плодотворной учебной деятельности учащихся, направленной на успешное развитие у них опыта творческой деятельности, является организация самостоятельной работы школьников в процессе обучения. Особенно важна такая самостоятельная работа, в ходе которой ученик должен постоянно переносить как известные, так и вновь конструируемые способы решения в новые ситуации познавательной деятельности. Методика организации такой работы является предметом обсуждения в этой главе.

Рассмотрим её на конкретных примерах, применяемых мною на уроках математики.

Самостоятельная работа учащихся это такой способ учебной работы, где:

учащимся предлагаются учебные задания и руководства для их выполнения,
работа проводится без непосредственного участия учителя, но под его руководством,
выполнение работы требует от учащихся умственного напряжения.

Самостоятельная работа активизирует учащихся в том смысле, что все ученики, даже более пассивные и ленивые, должны выполнять задания сами.

Учебные задания для самостоятельной работы разнообразны, они зависят от учебных умений учащихся. Сильные ученики владеют рациональными и более сложными учебными умениями. Слабые же ученики ограничиваться в основном умениями, связанными с репродуцирующей деятельностью.

Учебные задания делятся на 4 логических основания:

1) по методу самостоятельной работы учащихся (наблюдения, упражнения, работа с учебникомнаблюдения, 1) по методу ениями, связанными с репродуцирующей деятельностью. );

по звеньям учебного процесса (задания на восприятие, систематизацию, закрепление и повторение учебного материала);
по характеру познавательной деятельности учащихся (репродуцирующие и творческие задания);
по характеру руководства (подробное или менее подробное инструктирование).

По характеру учебной самостоятельной деятельности учащихся можно выделить четыре вида работ исходя из постепенного повышения уровня самостоятельности.

Первый уровень – простейшая самостоятельность ( по образцу)

Ученик выполняет упражнение, требующее простого воспроизведения имеющихся знаний по правилу, по образцу, самостоятельно решает задачи, упражнения на его примере.

Вот так, к примеру, мои ученики изучали тему «Квадратные уравнения». Предварительно на занятиях с учениками выполнялось такое задание:

В ходе решения давались образцы рассуждения и оформления решений. Вот образцы.

Рассмотрим решение каждого из данных уравнений.

1. Перенесём свободный член в правую часть уравнения: 4х 2 = 9.

2. Разделим обе части получившегося уравнения на 4: х 2 = 9/4.

3. Найдём корни х = 1,5 или х = — 1,5

Ответ: х 1 = 1,5, х 2 = — 1,5.

Перенесём свободный член в правую часть уравнения: 4х 2 = — 9.

2. Разделим обе части получившегося уравнения на 4: х 2 = -9/4.

3. Так как квадрат числа не может быть отрицательным числом, то получившееся уравнение не имеет корней. А следовательно, не имеет корней и равносильное ему уравнение 4х 2 + 9 = 0.

4. Ответ: корней нет.

Разложим левую часть уравнения на множители: х(3х — 4) = 0.
Произведение х(3х — 4) равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю: х = 0 или 3х – 4 = 0.
Решаем уравнение 3х – 4 = 0

4. Ответ: х 1 = 0, х 2 = 1 1 / 3 .

Данное уравнение равносильно уравнению х 2 = 0 и поэтому имеет единственный корень 0.

После чего записывается таблица № 1 (смотри приложение). Теперь учащимся предлагается самостоятельно решить аналогичные примеры: а) 2х 2 – 8 = 0;

Как видим, выполняя самостоятельные работы этого вида, учащимся необходимо сделать прямой перенос известного способа деятельности в аналогичной внутрипредметной ситуации.

Второй уровень – реконструктивно – вариативная самостоятельность.

Это проявляется в умении из нескольких имеющихся правил, определений, образцов рассуждений и т. п. выбрать одно определение и использовать его в процессе самостоятельного решения новой задачи. На данном уровне учащийся показывает умение производить мыслительные операции, такие как сравнение, анализ. Анализируя условия задачи, ученик перебирает имеющиеся в его распоряжении средства для её решения, сравнивает их и выбирает более действенное с некоторой модификацией в необычную внутрипредметную и межпредметную проблемную ситуацию.

Например, математические задачи решаются с помощью переноса способа решения геометрических задач.

Рассмотрим решение одной такой задачи, которую я даю учащимся при изучении темы «Квадратные уравнения».

«Площадь круга равна 1 дм 2 . Найти радиус круга».

Проследим, какие геометрические и математические знания потребуются, чтобы решить задачу. Прежде всего чтобы решить задачу нужно знать формулу площади круга S = πr 2 . Затем уметь выражать одну переменную через другую (радиус через площадь), т. е. r 2 = S/π. Подставив числовое значение, ученик получает, что r 2 = 1/π, где r = 1/√π , после чего надо освободиться от иррациональности в знаменателе дроби.

В этой задаче ученики самостоятельно определяют связь между геометрическими величинами и знаниями по алгебре, сами отыскивают способ определения неизвестной величины.

Третий уровень — частично – поисковая самостоятельность.

Она проявляется в умении из имеющихся у него правил и предписаний для решения задач определённого раздела математики, формировать (комбинировать) обобщённые способы для решения более широкого класса задач, в том числе и из других разделов математики. В умении осуществлять перенос математических методов, рассмотренных в одном разделе, на решение задач из других разделов или из смежных учебных предметов; в стремлении найти «собственное правило», приём, способ деятельности; в поисках нескольких способов решения задачи и в выборе наиболее рационального, изящного; в варьировании условий задачи и сравнении соответствующих способов решения и т. п. Здесь уже существуют элементы творчества. Ученик на этом уровне обладает относительно большим набором приёмов умственной деятельности – умеет проводить сравнение, анализ, синтез, абстрагирование и т. п. В его деятельности значительное место занимает контроль результатов и самоконтроль. Он может самостоятельно спланировать и организовать свою учебную деятельность.

При изучении темы «Решение квадратных уравнений выделением квадрата двучлена» даю учащимся задание.

«Решить приведённое квадратное уравнение х 2 + 10х + 25 = 0».

Для решения этого задания учащиеся должны использовать несколько известных решений и скомбинировать их в нужном порядке в необычной проблемной ситуации, т. к. они ещё не знакомы с решением полных квадратных уравнений.

Внимательно посмотрев, они видят, что левую часть уравнения можно представить в виде квадрата двучлена и получают:

(х + 5) 2 = 0. Отсюда

Далее предлагаю ребятам решить ещё одно приведённое квадратное уравнение: х 2 – 6х – 7 = 0 (1).

Для решения этого уравнения учащиеся должны увидеть, что если к разности х 2 – 6х прибавить число 9, то полученное выражение можно записать в виде (х — 3) 2 , т. е. в виде квадрата двучлена. Значит к обеим частям уравнения (1) надо прибавить число 9, а свободный член перенести в правую часть. Получают: х 2 – 6х + 9 = 9 + 7.

Далее это уравнение надо преобразовать:

(х — 3) 2 = 16. Отсюда

х – 3 = — 4 или х – 3 = 4,

Ответ: х 1 = — 1, х 2 = 7.

Таким образом, ученику приходится дробить задачу на несколько проблем, а затем уже комбинировать способы их решения для получения общего результата.

Высший, четвёртый уровень самостоятельности – творческая, исследовательская.

Самостоятельные работы всех этих видов включают в себя определённые проблемные ситуации, стимулирующие и ориентирующие обучающегося на поиск теоретического знания различной степени сложности (по принципу нарастания) и способов деятельности.

Например, даю такую внутрипредметную исследовательскую задачу: «Линейным или квадратным является уравнение

5в( в – 2 ) х 2 + ( 5в – 2 ) х – 16 = 0 относительно х при: а) в = 1; б) в = 2; в) в = 0,4; г) в = 0?»

Решение: а) в = 1; 5х 2 + 3х – 16 = 0 квадратное уравнение;

б) в = 2; 0х 2 + 8х – 16 = 0, 8х – 16 = 0 – линейное уравнение;

в) в = 0,4; 2 (- 1,6)х 2 + 0х – 16 = 0, — 3,8х 2 – 16 = 0 – неполное квадратное уравнение;

г) в = 0; 0х 2 – 2х – 16 = 0, — 2х – 16 = 0 – линейное уравнение.

Далее предлагаю ребятам решить такое задание:

«При каких значениях параметра а уравнение а х( а х + 3) + 6 = х( а х — 6) является: а) квадратным; б) неполным квадратным; в) линейным?»

Решение : а х( а х + 3) + 6 = х( а х — 6),

а 2 х 2 + 3ах + 6 = ах 2 – 6х,

х 2 (а 2 — а) + 3х(а + 2) + 6 = 0.

а) Уравнение является полным квадратным,если

если а Є ( — ∞; — 2) U ( -2; 0 ) U ( 0; 1 ) U ( 1; + ∞ ), то исходное уравнение является квадратным.

б) Уравнение является неполным квадратным, если

если а = — 2, то исходное уравнение является неполным квадратным.

в) Уравнение является линейным, если

если а = 0 или а = 1, то исходное уравнение является линейным.

Самостоятельность решения заключается здесь в том, что ученик по заданному условию расчленяет общую задачу на несколько частных задач, определяет пути их решения, а затем результаты каждой из них объединяет, сопоставляет, комбинирует и получает общий результат.

Межпредметные исследовательские задачи в курсе математики, да и в других учебных курсах применяется довольно редко. Правда, следует заметить, что не все темы курса математики равноценны как источник межпредметных исследовательских задач. Например, такие темы, как «Функция», «Предел функции», «Производная», «Интеграл», имеют незначительное количество межпредметных исследовательских задач. Их необходимо органически вплетать в общую систему задач и связывать с изучаемой тематикой. Таковы виды самостоятельных работ, которые лежат в основе обучения школьников теоретическим знаниям как инструменту познания и умениям планировать собственную познавательную деятельность, контролировать её ход.

Каждый из перечисленных видов работ включает в себя определённые проблемные ситуации, стимулирующие и ориентирующие обучающегося на поиски теоретического знания различной степени сложности (по принципу нарастания) и способов деятельности. В зависимости от открытого способа решения, обучающийся направляет свои поиски на развитие и обоснование этого способа. Прежние знания и опыт самостоятельной познавательной и практической деятельности используются при этом в зависимости от условий задачи.

Самая высокая ступень – умение решать исследовательские задачи. Сюда входит умение самостоятельно формулировать задачи различной степени сложности в заданной ситуации, ставить проблемы и разрабатывать план их решения, определять поиск решения и строить его гипотезу.

Система разноуровневых заданий для организации самостоятельной

работы учащихся по теме «Квадратные уравнения»

Определение квадратного уравнения.

Неполные квадратные уравнения. (2ч)

I. Простейшая воспроизводящая самостоятельная работа