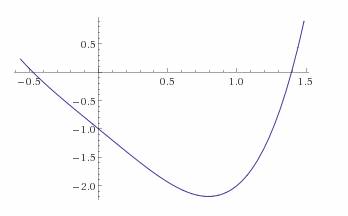
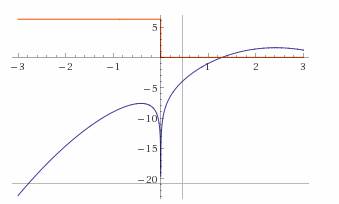
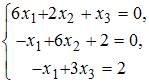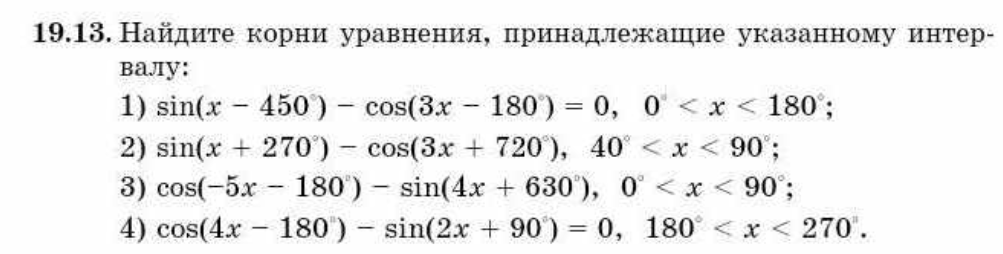Действительный корень уравнения принадлежит интервалу (3 видео)

Приближенное нахождение корней уравнения

Задание 2 . 1) Выбрав стартовую точку с координатами x01=0.5 и xo2=0.4, примените метод Ньютона–Рафсона, и с точностью e=0.000001 найдите минимум целевой функции:
Скачать решение
2) Выбрав ту же стартовую точку, примените метод наискорейшего спуска, и вновь найдите минимум целевой функции с точностью e=0.0001.

Пример №1 . Отделить корни аналитически и уточнить один из них методом половинного деления с точностью до 0,01.
Решение.
sin(x+3.14/3)-x/2=0. Скачать

Пример №2 . Определить и найти действительные корни с точностью до 0,001: а) x 4 – 2x – 1 = 0 — методами: 1) деления отрезка пополам; 2) касательных. б) 2log(x) — (x-2) 2 = 0 — методами: 1) хорд; 2) итераций.
Решение.
Найдем корни уравнения:
x 4 -2•x-1 = 0

Используем для этого Метод половинного деления (метод дихотомии).
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /₂(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /₂ n (b-a)
В качестве корня ξ. возьмем 1 /₂(a_n+b_n). Тогда погрешность определения корня будет равна (b_n – a_n)/2. Если выполняется условие:
(b_n – a_n)/2 1 /₂(a_n+b_n).
Уточним интервалы, в которых будут находиться корни уравнения. Для этого исходный интервал [-1;2] разобьем на 10 подынтервалов.
h₁ = -1 + 1*(2-(-1))/10 = -0.7
h₂ = -1 + (1+1)*(2-(-1))/10 = -0.4
Поскольку F(-0.7)*F(-0.4) 0, то a=-0.55
Итерация 2.
Находим середину отрезка: c = (-0.55 -0.4)/2 = -0.48
F(c) = 0.000907
F(x) = 0.19
Поскольку F(c)•F(x) > 0, то a=-0.48
Итерация 3.
Находим середину отрезка: c = (-0.48 -0.4)/2 = -0.44
F(c) = -0.0884
F(x) = 0.000907
Поскольку F(c)•F(x) 0, то a=1.25
Итерация 2.
Находим середину отрезка: c = (1.25 + 1.4)/2 = 1.33
F(c) = -0.57
F(x) = -1.06
Поскольку F(c)•F(x) > 0, то a=1.33
Итерация 3.
Находим середину отрезка: c = (1.33 + 1.4)/2 = 1.36
F(c) = -0.28
F(x) = -0.57
Поскольку F(c)•F(x) > 0, то a=1.36
Итерация 4.
Находим середину отрезка: c = (1.36 + 1.4)/2 = 1.38
F(c) = -0.12
F(x) = -0.28
Поскольку F(c)•F(x) > 0, то a=1.38
Остальные расчеты сведем в таблицу.

N	c	a	b	f(c)	f(x)
1	1.25	1.1	1.4	-1.06	-1.06
2	1.33	1.25	1.4	-0.57	-0.57
3	1.36	1.33	1.4	-0.28	-0.28
4	1.38	1.36	1.4	-0.12	-0.12
5	1.39	1.38	1.4	-0.0415	-0.0415
6	1.4	1.39	1.4	-0.000217	-0.000217
7	1.4	1.4	1.4	-0.000217	0.0206
8	1.4	1.4	1.4	-0.000217	0.0102
9	1.4	1.4	1.4	-0.000217	0.00498

Ответ:
x = 1.4; F(x) = 0.00498
Количество итераций, N = 9
Параметр сходимости.
α = (1.4 — 1.4)/9 = 6.5E-5

Посмотрите как можно быстро решить задачу.

Содержание

Тема: Вычисление определителей
Задача 54522 найдите корни уравнения,принадлежащие.
Условие
Решение
🎥 Видео

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Тема: Вычисление определителей

Определитель равен …

	– 30
– 15

Тема: Системы линейных уравнений: основные понятия

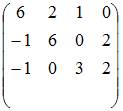
Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1.
2.
3.
4.

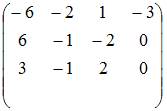Действительный корень уравнения принадлежит интервалу

Тема: Скалярное произведение векторов

Векторы и перпендикулярны при m, равном …

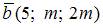
	– 2,5
– 5/3
5/3
2,5

Тема: Интерполирование функций: интерполяционный многочлен Лагранжа

График функции проходит через точки

Тогда ее интерполяционный многочлен второго порядка равен …

Тема: Численное дифференцирование и интегрирование

Значение функции в точке можно вычислить по формуле …

Тема: Численные методы решения алгебраических уравнений

Три итерации метода половинного деления при решении уравнения на отрезке требуют последовательного вычисления значений функции в точках …

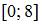
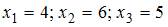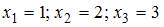Тема: Численные методы анализа

Действительный корень уравнения принадлежит интервалу …

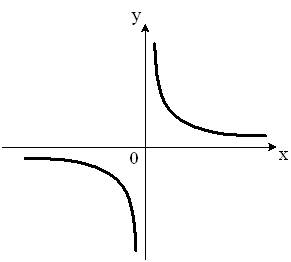
Тема: Элементы гармонического анализа

Укажите график периодической функции

Тема: Формы записи комплексного числа

Модуль комплексного числа равен …

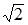Тема: Периодические функции

Установите соответствие между периодической функцией и значением ее периода

1.
2.
3.

Тема: Операции над комплексными числами

Если , , то равно …

Тема: Ряд Фурье. Теорема Дирихле

Функция , заданная на отрезке является четной. Тогда разложение этой функции в ряд Фурье может иметь вид …

Тема: Определение функции комплексного переменного

Значение функции в точке равно …

	– 9 – 15i
15 – 9i
15 – 15i
– 9 – 9i

Тема: Основные понятия теории вероятностей

Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее трех очков, равна …

Тема: Теоремы сложения и умножения вероятностей

Случайные события А и В – несовместны. Тогда выполнено равенство …

Тема: Точечные оценки параметров распределения

Проведено 5 измерений (без систематических ошибок) некоторой случайной величины (в мм): 9, 10, 11, 13, 14. Тогда несмещенная оценка математического ожидания равна …

	11,4
14,25
11,2

Тема: Характеристики вариационного ряда

Мода вариационного ряда 2 , 3 , 4 , 7 , 8 , 8 , 9 равна …

Тема: Статистическое распределение выборки

Из генеральной совокупности извлечена выборка объема n=50:

Тогда n₃ равен …

Тема: Полная вероятность. Формула Байеса

В первой урне 3 белых и 7 черных шаров. Во второй урне 4 белых и 6 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна …

	0,35
0,05
0,4
0,7

Тема: Линейные дифференциальные уравнения 2 порядка

Частному решению линейного неоднородного дифференциального по виду его правой части соответствует функция …

Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Задача 54522 найдите корни уравнения,принадлежащие.

Условие

найдите корни уравнения,принадлежащие указанному интервалу

Решение

По свойству [i]периодичности[/i] синуса и косинуса
sin(x+[b]n* 360 °[/b] )=sinx
n∈ Z
cos(x+[b]n* 360[/b] ° )=cosx
n∈ Z

1)
Так как
sin(x-450 ° )=sin(x-90 ° -360 ° )=sin(x-90 °)=-sin(90 ° -x)=-cosx
и
cos(3x-180 ° )=cos(180 ° -3x)=-cos 3x

Уравнение принимает вид:

[red]-сosx-(-cos3x)=0[/red]
cos3x — cosx=0
-2sin2x*sinx=0

sin2x=0 ⇒ 2x=πn, n ∈ Z ⇒[b] x=(π/2)*n, n ∈ Z[/b]

sinx=0 ⇒[b] x=πk, k ∈ Z [/b]

О т в е т. [b] x=(π/2)*n, n ∈ Z[/b];[b] x=πk, k ∈ Z [/b]
интервалу [b] (0; 180 ° )[/b] принадлежит корень
[b](π/2)=90 °[/b], получен из серии [b] x=(π/2)*n, n ∈ Z[/b] при n=1

2)
Так как
sin(x+270 °)=sin(x+360 ° -90 ° )=sin(x -90 °)=-sin(90 °-x)=- cosx
cos(3x+720 ° )=cos3x

Опечатка в условии задачи, нет [b]0[/b] справа
Уравнение:

cos2x=0 ⇒ 2x=(π/2)+πn, n ∈ Z ⇒[b] x=(π/4)+(π/2)*n,, n ∈ Z[/b]

cosx=0 ⇒ [b]x=(π/2)+πk, k ∈ Z [/b]

О т в е т. [b] x=(π/4)+(π/2)*n,, n ∈ Z[/b];[b]x=(π/2)+πk, k ∈ Z [/b]

интервалу (40 ° ; 90 ° ) принадлежит корень
[b]x=(π/4)=45 °[/b] , получен из серии x=(π/4)+(π/2)*n,, n ∈ Z при n=1

3)
По свойству четности косинуса:
cos(-5x-180 ° )=cos(180 ° +5x)
По формулам приведения
cos(180 ° +5x)=-cos5x

По свойству периодичности и формулам приведения
sin(4x+630 ° )=sin(4x+720 ° -90 ° )=sin(4x-90 ° )=по свойству нечетности синуса=-sin(90 ° -4x)
по формулам приведения=-cos4x
Уравнение:
[red]-cos5x-(-cos4x)=0[/red]

-2sin(5x+4x)/2 * sinx(5x-4x)/2=0
-2sin(9x)/2 * sinx(x)/2=0

sin(9x/2)=0 ⇒ (9x/2)=πk, k ∈ Z ⇒ [b]x=(2/9)πk, k ∈ Z[/b]
sinx(x)/2=0⇒ (x/2)=πn, n ∈ Z ⇒ [b]x=2πn, n ∈ Z[/b]

О т в е т. [b]x=(2/9)πk, k ∈ Z[/b]; [b]x=2πn, n ∈ Z[/b]
интервалу (0 ° ; 90 ° ) принадлежат корни
[b]x=(2π/9)=40 °[/b] , получен из серии (2/9)πk, k ∈ Z[/b] при k=1
и
[b]x=(4π/9)=80 °[/b] , получен из серии (2/9)πk, k ∈ Z[/b] при k=2

4)
По свойству четности косинуса:
cos(4x-180 ° )=cos(180 ° -4x)=
по формулам приведения:
=-cos4x

по формулам приведения:
sin(2x+90 °) =cos2x

Уравнение:
[red]-cos4x-cos2x=0[/red]
cos4x+cos2x=0
2cos(4x+2x)/2 * сos(4x-2x)/2=0

cos3x=0 ⇒ 3x=(π/2)+πn, n ∈ Z ⇒ [b]x=(π/6)+(π/2)*n, n ∈ Z[/b]
cosx=0 ⇒ [b]x=(π/2)+πk, k ∈ Z[/b]

О т в е т
[b]x=(π/6)+(π/2)*n, n ∈ Z[/b]; [b]x=(π/2)+πk, k ∈ Z[/b]
интервалy (180 ° ; 270 ° ) принадлежит корень
[b] x=(π/6)+π=210 °[/b] , получен из серии x=(π/6)+(π/2)*n, n ∈ Z при n=2