Действительная полуось гиперболы заданной уравнением 25х2 16у2 400 равна

Глава III. Кривые второго порядка

§ 43. Уравнения эллипса, гиперболы и параболы
в других (неканонических) системах координат

Применим выведенные в § 13 формулы перехода от одной прямоугольной декартовой системы координат к другой для изучения неканонических уравнений гиперболы, параболы, эллипса.

1) Рассмотрим уравнение

Из школьного курса известно, что уравнение (1) называется уравнением гиперболы и имеет график, изображенный на рис. 121.

Посмотрим, каким будет уравнение этой гиперболы в другой системе координат, в системе, которая получается из исходной поворотом базисных векторов на угол α = 45°.

В данном случае старые координаты х и у выражаются через новые х‘ и у‘ следующим образом:

Заменяя в уравнении (1) старые переменные новыми, получаем

Мы получили каноническое уравнение равносторонней гиперболы. Следовательно, уравнение (1) задает равностороннюю гиперболу. Старые оси координат являются асимптотами гиперболы, поэтому уравнение (1) называют уравнением гиперболы, отнесенным к асимптотам (см. рис. 121). Сравнивая уравнения (1) и (2), видим, что действительная ось гиперболы, заданной уравнением (1), равна √ 2а .

Новая система координат О, i’, j’ называется канонической, так как в ней уравнение гиперболы имеет канонический вид.

Уравнение ху = а, а 2 — у 2 = 18. Написать ее уравнение, отнесенное к асимптотам.

Выполним поворот на угол α == —45°. Тогда старше координаты выражаются через новые по формулам

Подставив в данное уравнение значения х и у, получим

или после упрощения х’у’ = 9.

2) Рассмотрим уравнение

Вам хорошо знакомо это уравнение и его график: парабола с осью, параллельной оси ординат. Записав уравнение (3) в виде

(4)

находим координаты вершины параболы

Перейдем к новой системе координат, направления осой которой совпадают с направлениями осей старой системы, а начало координат О’ находится в вершине параболы. Точка О’ имеет, следовательно, координаты (). Положив в формулах переноса

Так выражаются в данном случае старые координаты x и у через новые х’ и у’. Заменяя в уравнении (4) старые координаты новыми, приходим к уравнению

Итак, если парабола в некоторой системе координат имеет уравнение (3), то всегда можно перейти к новой системе координат, в которой уравнение параболы будет иметь более простой вид: y’ = αx‘ 2 , α =/= 0. Более того, всегда можно выбрать систему координат так, чтобы коэффициент в уравнении параболы был положителен. В самом деле, пусть α 2 . Полагая α₁ = — α, получаем y» = α₁x» 2 , где α₁ > 0.

3) Пусть в некоторой системе координат парабола задана уравнением

Перейдем к новой системе координат, которая получается из исходной поворотом базисных векторов на угол α = 90° (рис. 123).

Формулы поворота в этом случае принимают вид

Применяя в уравнении (5) старые координаты новыми, получаем

Обозначим 1 /_α через 2р, тогда

Мы получили каноническое уравнение параболы. Таким образом, уравнением (5) задается парабола с фокальным параметром, равным 1 /_2α .

Из результатов, полученных в пункте 2), следует, что фокальный параметр параболы, заданной уравнением y = αx 2 + βx + γ, α =/=0 , равен 1 /_{2 |α |} .

Задача 2. Дано уравнение параболы y = 2x 2 + 6x + 7.

Привести его к каноническому виду. Найти расстояние от фокуса параболы до ее директрисы.

Выделим полный квадрат в правой части данного уравнения

Координаты вершины параболы (— 3 /₂ ; 5 /₂ ).

Перейдем к новой системе координат, которая получается из исходной переносом начала координат в точку O’ (— 3 /₂ ; 5 /₂ ) и поворотом базисных векторов на угол α = 90°
(рис. 124).

По формулам (3) § 13 получаем

Подставив эти значения х и у в уравнение параболы, получим

Из полученного уравнения видно, что расстояние от фокуса параболы до директрисы (фокальный параметр) равно 1 /_{4 .}

4) Рассмотрим уравнение

(6)

Это уравнение похоже на каноническое уравнение эллипса, но не является таковым, так как в каноническом уравнении эллипса а > b.

Перейдем от системы координат хОу к системе х’Оу’, которая получается из исходной системы поворотом базисных векторов на угол α = 90°. Формулы поворота в этом случае имеют вид

Поэтому в новой системе данное уравнение запишется так:

Мы получили каноническое уравнение эллипса. Следовательно, уравнением (6) задается эллипс, большая ось которого лежит на оси Оу, малая на оси Ох. Фокусы такого эллипса расположены в точках F₁(0; с) и F₂(0; —с), где с = √ b 2 — a 2 (рис. 125).

Задача 3. Доказать, что кривая, заданная уравнением

является эллипсом. Найти его полуоси и координаты фокусов. Дать чертеж.

Преобразуем данное уравнение к виду:

25 (х — 1) 2 + 16 (у + 2) 2 = 400.

Oт системы координат хОу перейдем к системе х’О’у’, сохранив направление осей, а начало координат поместив и точку О’(1; —2). Тогда старые и новые координаты будут связаны формулами переноса

Поэтому в новой системе координат кривая имеет уравнение

Итак, данная кривая является эллипсом, полуоси которого равны 5 и 4. Полуфокусное расстояние с = √ 25—16 =3. Фокусы эллипса в новой системе имеют координаты (0; 3) и (0; —3). По формулам переноса находим их координаты в старой системе:
(1; 1) и (1; —5). Чертеж дан на рис. 126.

Задача 4. Написать уравнение эллипса, одна ось которого принадлежит оси ординат и равна 12, а другая ось принадлежит оси абсцисс и равна 8.

По условию задачи b = 6, а = 4, следовательно,

Задача 5. Написать уравнение эллипса, одна ось которого принадлежит оси ординат и равна 20, а расстояние между фокусами равно 16. Центр эллипса находится в точке
(0; 0).

Искомое уравнение эллипса можно записать в виде

Так как 2с = 16, 2b = 20, то с = 8, b = 10, а так как фокусы расположены на оси Оу, то
а 2 = b 2 — c 2 = 100 — 64 = 36 .Следовательно, эллипс имеет уравнение

Задача 6. Найти длины полуосей эллипса 25х 2 + 16у 2 = 400 и вычислить координаты его фокусов.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Найти полуоси координаты фокусов и эксцентриситет и уравнение директрис эллипса 16х ^ 2 + 25y ^ 2 — 400 = 0?

Математика | 10 — 11 классы

Найти полуоси координаты фокусов и эксцентриситет и уравнение директрис эллипса 16х ^ 2 + 25y ^ 2 — 400 = 0.

Приведем уравнение к канонческой форме : Разделим обе части на 400.

Получим : x ^ 2 / 25 + y ^ 2 / 16 = 1.

Соответственно, большя полуось = 5, малая = 4.

Видео:§23 Построение гиперболыСкачать

Дан эллипс x ^ 2 / 7 + y ^ 2 / 16 = 1?

Дан эллипс x ^ 2 / 7 + y ^ 2 / 16 = 1.

Найдите его эксцентриситет.

Видео:Видеоурок "Гипербола"Скачать

Записать уравнение окружности, проходящей через фокусы эллипса 24х2 + 25у2 = 600 и имеющей центр в точке А(0 ; 6)?

Записать уравнение окружности, проходящей через фокусы эллипса 24х2 + 25у2 = 600 и имеющей центр в точке А(0 ; 6).

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Дан эллипс 9x² + 25y² = 225 найти а) его полуоси б) фокусы в) эксцентриситет г) уравнения директрис?

Дан эллипс 9x² + 25y² = 225 найти а) его полуоси б) фокусы в) эксцентриситет г) уравнения директрис.

Видео:165. Найти фокусы и эксцентриситет эллипса.Скачать

Составьте уравнение эллипса, фокусы которого лежат на оси ординат, E = 0, 6 и 2b = 10 ?

Составьте уравнение эллипса, фокусы которого лежат на оси ординат, E = 0, 6 и 2b = 10 .

Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Составить уравнение эллипса, у которого эксцентриситет равен 0, 8, а фокальные радиусы одной из его точек равны 2 и 3?

Составить уравнение эллипса, у которого эксцентриситет равен 0, 8, а фокальные радиусы одной из его точек равны 2 и 3.

Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Составить каноническое уравнение эллипса, если известно, что расстояние между фокусом равна 6, а большая полуось — 5 единицам?

Составить каноническое уравнение эллипса, если известно, что расстояние между фокусом равна 6, а большая полуось — 5 единицам.

Видео:Алгебра 8 класс (Урок№14 - Функция y = k/x и её график.)Скачать

Построить кривую, заданную уравнением?

Построить кривую, заданную уравнением.

Найти : а) полуоси (для эллипса и гиперболы) ; б) координаты фокусов ; в) эксцентриситет (для эллипса и гиперболы) ; г) уравнения директрис.

Уравнения кривой y2(в квадрате) + 4х — 4 = 0.

Видео:Гипербола. Функция k/x и её графикСкачать

Составить каноническое уравнение эллипса, если его большая полуось равна 12, а эксцентриситет равен 0, 8?

Составить каноническое уравнение эллипса, если его большая полуось равна 12, а эксцентриситет равен 0, 8.

Найти расстояние между фокусами эллипса.

Видео:182 Алгебра 9 класс. Найдите Асимптоты гиперболы.Скачать

Составить каноническое уравнение параболы с вершиной в начале координат, симметричной ОУ , фокус которой в точке F(0 ; — 3) Составить уравнение эллипса , проходящего через точку А(4 ; 6) , фокусы кото?

Составить каноническое уравнение параболы с вершиной в начале координат, симметричной ОУ , фокус которой в точке F(0 ; — 3) Составить уравнение эллипса , проходящего через точку А(4 ; 6) , фокусы которого совпадают с фокусами гиперболы x ^ 2 — y ^ 2 = 8.

Видео:§21 Каноническое уравнение гиперболыСкачать

Эксцентриситет эллипса 5х ^ 2 + 9y ^ 2 = 45 равен?

Эксцентриситет эллипса 5х ^ 2 + 9y ^ 2 = 45 равен.

Вы перешли к вопросу Найти полуоси координаты фокусов и эксцентриситет и уравнение директрис эллипса 16х ^ 2 + 25y ^ 2 — 400 = 0?. Он относится к категории Математика, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Математика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

2000 + 4000 = 6000 6000 — (2986 + 1350) = 1682.

№252 1)5² + 12² = 5×5 + 12×12 = 25 + 144 = 166 2)16² — 11² = 16×16 — 11×11 = 256 — 121 = 135 3)2³ + 9³ = 2×2×2 + 9×9×9 = 8 + 729 = 737 4)10³ — 3³ = 10×10×10 — 3×3×3 = 1000 — 27 = 973 №253 1)3×10² + 7×10 + 9 = 3×100 + 70 + 9 = 300 + 79 = 379 2)5×10³ +..

А. 32х = 453 + 59 32х = 512 х = 16 б. Умножить левую и правую часть на 23, и получится у + 7176 = 8970 у = 8970 — 7176 у = 1794 в. 7035 = 67(120 — х) 105 = 120 — х х = 120 — 105 х = 15.

7 — 6 = 1 7 — 5 = 2 значит сосуд 5 литров нужно разделить на 5 делений и одно деление заполнить и вылить в 7л и еще полные 5л вылить в 7л.

1) 24 / 25 и 15 / 25 2) 11 / 36 и 21 / 36 3) 30 / 40 и 19 / 40 4) 35 / 42 и 31 / 42 5) 18 / 40 и 13 / 40 6) 68 / 100 и 1 / 100 7) 69 / 96 и 1 / 96 8) 138 / 140 и 139 / 140.

1 7 * 3 = 3 / 21 3 / 218 / 15 3 / 5 * 3 = 9 / 15 9 / 15>8 / 15 3 / 5>11 / 20 3 / 5 * 4 = 12 / 20 12 / 20>11 / 20 И т. Д.

А)Находишь НОЗ — это число, которое делится и на 7 , и на 21. В данном задании — это 21. Числитель и знаменатель первой дроби умножаешь на 3(21 / 7 = 3 — дополнительный множитель ), получаешь 3 / 21 меньше, чем 4 / 21 так, как из двух дробей с один..

420км = 42 000 000см 42000000 / 3, 5 = 12 000 000 ответ 1 : 12 000 000 87, 5км = 8 750 000см 8750000 / 3, 5 = 2 500 000 ответ 1 : 2 500 000.

4× — 128 × 13 = 52 4× — 1664 = 52 4× = 52 + 1664 4× = 1716 × = 1716÷4 × = 429.

4×X — 128×13 = 52 1) 128×13 = 1664 2)1664 + 52 = 1716 3)1716 : 4 = 429 4)4×429 = Блин! Мне кажется у меня не правильно.

Видео:ХИМИЯ С НУЛЯ — Как решать задачи по Химии на Массовую ДолюСкачать

Математический портал

Видео:Функция y=k/x и ее график. 7 класс.Скачать

Nav view search

Navigation

Search

• Вы здесь:
• Home

Видео:Установление эмпирической и молек. формул по массовым долям элем., входящих в состав в-ва. 10 класс.Скачать

Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Эллипс.

Эллипс с каноническим уравнением $frac+frac=1, ageq b>0,$ и меет форму изображенную на рисунке.

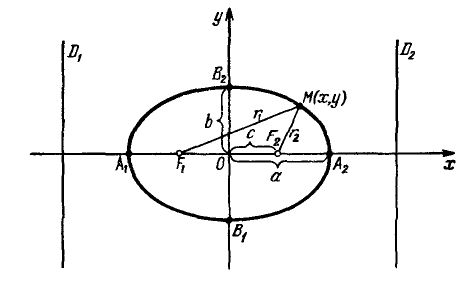
Параметры $a$ и $b$ называются полуосями эллипса (большой и малой соответственно). Точки $A_1(-a, 0),$ $A_2(a, 0), $ $B_1(0, -b), $ и $B_2(0, b), $ его вершинами. Оси симметрии $Ox$ и $Oy$ — главными осями а центр симметрии $O -$ центром эллипса.

Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами эллипса векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей эллипсу. В частном случае $a=b$ фокусы $F_1$ и $F_2$ совпадают с центром, а каноническое уравнение имеет вид $frac+frac=1,$ или $x^2+y^2=a^2,$ т.е. описывает окружность радиуса $a$ с центром в начале координат.

Прямые $D_1: x=-a/e$ и $D_2: x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами эллипса.

Теорема. ( Директориальное свойство эллипса)

Эллипс является множеством точек, отноше ние расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно $e.$

Примеры.

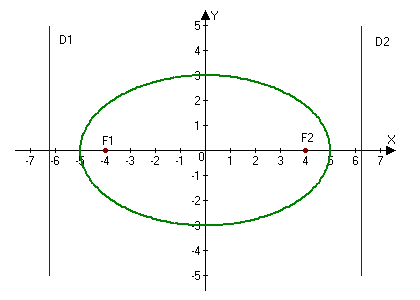
2.246. Построить эллипс $9x^2+25y^2=225.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.

Приведем уравнение эллипса к каноническому виду:

а) Находим полуоси $a=5,$ $b=3.$

б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$

$c=sqrt=sqrt=4Rightarrow F_1(-4, 0),qquad F_2(4, 0).$

г) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Ответ: а) $a=5,$ $b=3;$ б) $ F_1(-4, 0),qquad F_2(4, 0);$ в) $e=frac;$ г) $D_1: x=-frac$ и $D_2: x=frac.$

2.249 (a). Установить, что уравнение $5x^2+9y^2-30x+18y+9=0$ определяет эллипс, найти его центр $C,$ полуоси, эксцентриситет и уравнения директрис.

Приведем уравнение эллипса к каноническому виду, для этого выделим полные квадраты:

Это уравнение эллипса. Центр имеет координаты $C=(x_0, y_0)=(-3, -1);$ полуоси $a=3,$ $b=sqrt 5.$

Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-frac=-frac $ и $D_2: x=frac=frac.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$

Ответ: $C=(x_0, y_0)=(-3, -1);$ $a=3,$ $b=sqrt 5;$ $ e=frac.$ $D_1:2x+3=0, $ $D_2: 2x-15=0.$

2.252. Эллипс, главные оси которого совпадают с координатными осми, проходят через точки $M_1(2, sqrt 3)$ и $M_2(0, 2).$ Написать его уравнение, найти фокальные радиусы точки $M_1$ и расстояния этой точки до директрис.

Решение.

Поскольку оси эллипса совпадают с координатными осями, то центр эллипса совпадает с началом координат. Следовательно, из того, что точка $(0, 2)$ принадлежит эллипсу, можно сделать вывод, что $b=2.$

Далее, чтобы найти $a,$ подставим найденное значение $b$ и координаты точки $M_1(2, sqrt 3)$ в каноническое уравнение эллипса $frac+frac=1:$

Таким образом, уравнение эллипса $frac+frac=1.$

Далее найдем координаты фокусов:

$c=sqrt=sqrt=2sqrt 3Rightarrow F_1(-2sqrt 3, 0),,,, F_2(2sqrt 3, 0).$

Отсюда находим $overline =(2+2sqrt 3, sqrt 3),$ $overline=(2-2sqrt 3, sqrt 3).$

Чтобы найти расстояния от точки $M_1$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$

Таким образом, расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_1: sqrt 3 x+8=0$

расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_2: sqrt 3 x-8=0$

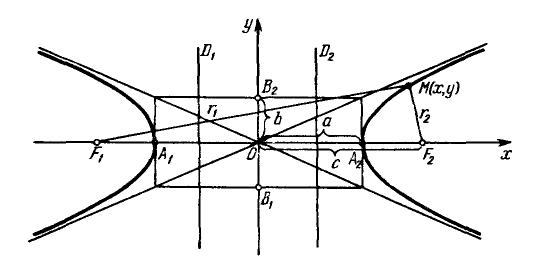
Параметры $a$ и $b$ называются полуосями гиперболы. Точки $A_1(-a, 0),$ $A_2(a, 0) — $ ее вершинами. Оси симметрии $Ox$ и $Oy$ — действительной и мнимой осями а центр симметрии $O -$ центром гиперболы.

Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами гиперболы, векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей гиперболе.

Прямые $D_1: x=-a/e$ и $D_2:x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами гиперболы.

Теорема. (Директориальное свойство гиперболы).

Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей дирек трисы постоянно и равно $e.$

Примеры.

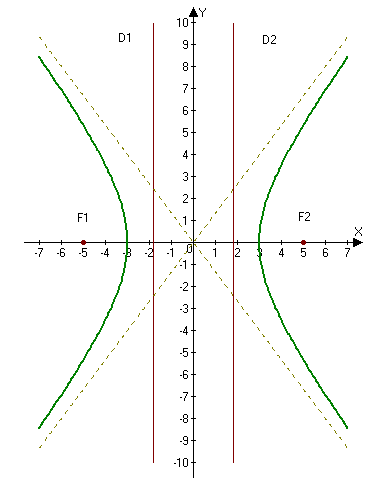
2.265. Построить гиперболу $16x^2-9y^2=144.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.

Приведем уравнение гиперболы к каноническому виду:

а) Находим полуоси $a=3,$ $b=4.$

б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$

$c=sqrt=sqrt=5Rightarrow F_1(-5, 0),qquad F_2(5, 0).$

г) Асимптоты гиперболы находим по формулам $y=pmfracx:$

д) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Ответ: а) $a=3,$ $b=4;$ б) $ F_1(-5, 0),qquad F_2(5, 0);$ в) $e=frac;$ г) $y=pmfracx;$ д ) $D_1: x=-frac$ и $D_2: x=frac.$

2.269 (a). Установить, что уравнение $16x^2-9y^2-64x-54y-161=0$ определяет гиперболу, найти ее центр $C,$ полуоси, эксцентриситет, уравнения асимптот и директрис.

Приведем заданное уравнение к каноническому виду, для этого выделим полные квадраты:

Это уравнение гиперболы. Центр имеет координаты $C=(x_0, y_0)=(2,-3);$ полуоси $a=3,$ $b=4.$

Асимптоты гиперболы c центром в начале координат, находим по формулам $y=pmfracx,$ а с центром в точке $C=(x_0, y_0) -$ по формуле $y-y_0=pmfrac(x-x_0),$

$$y+3=frac(x-2)Rightarrow 3y+9=4x-8Rightarrow 4x-3y-17=0.$$

$$y+3=-frac(x-2)Rightarrow 3y+9=-4x+8Rightarrow 4x+3y+1=0.$$

Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-frac=-frac $ и $D_2: x=frac=frac.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$

Ответ: $C=(2, -3);$ $a=3,$ $b=4;$ $ e=frac,$ $4x-3y-17=0,$ $4x+3y+1=0,$ $D_1:5x-1=0, $ $D_2: 5x-19=0.$

2.272. Убедившись, что точка $M(-5, 9/4)$ лежит на гиперболе $frac-frac=1,$ найти фокальные радиусы этой точки и расстояния этой точки до директрис.

Решение.

Проверим, что заданная точка лежит на гиперболе:

Следовательно, точка $M(-5, 9/4)$ лежит на гиперболе $frac-frac=1.$

Для того, чтобы найти фокальные радиусы, найдем фокусы гиперболы:

$c=sqrtRightarrow c=sqrt=sqrt =5$ Следовательно, фокусы имеют координаты $F_1(-5, 0), F_2(5, 0).$

Фокальные радиусы точки, можно найти по формулам $r_1=|overline|$ и $r_2=|overline|.$

Чтобы найти расстояния от точки $M$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-fracRightarrow x=-fracRightarrow 5x+16=0;$

$D_2: x=fracRightarrow x=fracRightarrow 5x-16=0;$

Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$

Таким образом, расстояние от точки $M(5, 9/4)$ до прямой $D_1: sqrt 5x+16=0$

расстояние от точки $M(5, 9/4)$ до прямой $D_2: sqrt 5x-16=0$

Ответ: $r_1=9/4,$ $r_2=frac;$ $d_1=frac;$ $d_2=frac.$

2.273. Найти точки гиперболы $frac-frac=1,$ находящиеся на расстоянии $7$ от фокуса $F_1.$

Решение.

Из уравнения гиперболы находим полуоси: $a=3, , b=4.$ Следовательно, $c=sqrtRightarrow c=sqrt=sqrt =5.$

Отсюда находим $F_1=(-5, 0).$

Геометрическое место точек, расположенных на расстоянии $7$ от фокуса $F_1,$ это окружность с центром в точке $F_1=(-5, 0)$ и радиусом $r=7:$

Чтобы н айти точки гиперболы $frac-frac=1,$ находящиеся на расстоянии $7$ от фокуса $F_1,$ решим систему уравнений

Решим уравнение $5x^2+18x-72=0:$

Находим соответствующие координаты $y:$ $y_1=pmsqrt=sqrt$ — нет корней .

Ответ: $(-6, pm4sqrt 3).$

Парабола.

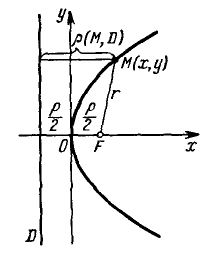
Парабола с каноническим уравнением $y^2=2px, p>0,$ и меет форму изображенную на рисунке.

Число $p$ называется параметром параболы. Точка $O -$ ее вершиной, а ось $Ox$ — осью параболы.

Точка $Fleft(frac

, 0right)$ называется фокусом параболы, вектор $overline -$ фокальным радиус-векторам, а число $r=|overline| -$ фокальным радиусом точки $M,$ принадлежащей параболе.

Прямая $D: x=-p/2$ перпендикулярная оси и проходящая на расстоянии $p/2$ от вершины параболы, называется ее директрисой.

Примеры.

2.285 (а). Построить параболу $y^2=6x$ и найти ее параметры.

Решение.

Параметр $p$ параболы можно найти из канонического уравнения $y^2=2px: $

$$y^2=6xRightarrow y^2=2cdot 3xRightarrow p=2.$$

Ответ: $p=3.$

2.286 (а). Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси $Ox$ и $p=1/2.$

Решение.

Поскольку парабола расположена в левой полуплоскости, симметрично относительно оси $Ox,$ то уравнение параболы будет иметь вид $y^2=-2px.$ Подставляя заданное значение параметра, находим уравнение параболы:

Ответ: $y^2=-x.$

2.288 (а). Установить, что уравнение $y^2=4x-8$ определяет параболу, найти координаты ее вершины $A$ и величину параметра $p.$

Решение.

Уравнение параболы, центр которой сдвинут в точку $(x_0, y_0),$ имеет вид $(y-y_0)^2=2p(x-x_0)^2.$

Приведем заданное уравнние к такому виду:

Таким образом, $y^2=4(x^2-2)$ — парабола с центром в точке $(0, 2).$ Параметр $p=2.$

Ответ: $C(0, 2),$ $p=2.$

2.290. Вычислить фокальный параметр точки $M$ параболы $y^2=12x,$ если $y(M)=6.$

Решение.

Чтобы найти фокальный параметр точки $M,$ найдем ее координаты. Для этого подставим в уравнение параболы координату $y:$ $$6^2=12xRightarrow 36=12xRightarrow x=3.$$

Таким образом, точка $M$ имеет координаты $(3, 6).$

Из уравнения параболы $y^2=12x$ находим параметр параболы: $y^2=2cdot 6xRightarrow p=6.$ Следовательно фокус параболы имеет координаты $F(3, 0).$

Далее находим фокальный параметр точки:

Ответ: $6.$

2.298. Из фокуса параболы $y^2=12x$ под острым углом $alpha$ к оси $Ox$ направлен луч света, причем $tgalpha=frac.$ Написать уравнение прямой, на которой лежит луч, отраженный от параболы.

Решение.

Найдем координаты фокуса. Из канонического уравнения параболы $y^2=2px$ находим параметр: $y^2=12x=2cdot 6xRightarrow p=6.$

Координаты фокуса $F(p/2, 0)Rightarrow F(3,0).$

Далее находим уравнение прямой, которая проходит через точку $(3, 0)$ под углом $alpha: tgalpha=frac$ к оси $OX.$ Уравнение ищем в виде $y=kx+b,$ где $k=tgalpha=frac.$

Чтобы найти $b,$ в уравнение прямой подставим координаты точки $(3, 0):$

$0=fraccdot 3+bRightarrow b=-frac.$ Таким образом, уравнение луча, направленного из фокуса $y=fracx-frac.$

Далее, найдем точку пересечения найденной прямой с параболой:

Поскольку по условию луч падает под острым углом, то мы рассматриваем только положительную координату $y=18.$ Соответствующее значение $x=frac=frac=27.$

Таким образом, луч пересекает параболу в точке $(27, 18).$

Далее найдем уравнение касательной к параболе в найденной точке $(27, 18)$ по формуле $(y-y_0)=y'(x_0)(x-x_0):$

Подставляем все найденные значения в уравнение касательной:

$y-18=frac(x-27)Rightarrow 3y-54=x-27Rightarrow x-3y+27=0.$

Далее, найдем угол $beta$ между лучем $y=fracx-frac$ и касательной $x-3y+27=0.$ Для этого оба уравнения запишем в виде $y=k_1x+b_1$ и $y=k_2+b_2$ угол вычислим по формуле $tg(L_1, L_2)=frac$

$$L_2: x-3y+27=0Rightarrow y=fracx+9Rightarrow k_2=frac.$$

Легко увидеть, что угол между лучем $L_1,$ направленным из фокуса и его отражением равен $pi-2beta,$ а угол между отраженным лучем и осью $Ox$ $pi-(pi-2beta)-alpha=2beta-alpha.$

Зная $tgbeta=frac$ и $tgalpha=k_1=frac$ и вспоминая формулы для двойного угла тангенса и тангенс разности, находим $tg(2beta-alpha):$

$$tg(2beta-alpha)=frac=frac<frac-frac><1+fracfrac>=0.$$ Следовательно, прямая, содержащая отраженный луч параллельна оси $Ox.$ Так как она проходит через точку $(27, 18),$ то можно записать ее уравнение $y=18.$

📸 Видео

Самое нормальное распределение // Vital MathСкачать

✓ Четыре способа решить новую задачу из ЕГЭ | Задание 10. Демоверсия ЕГЭ-2023 | Борис ТрушинСкачать

Сумма ряда 1/n^2. Олдскульный способ Эйлера для решения Базельской задачиСкачать

Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать