Давление паров ртути в зависимости от температуры выражается уравнением (8 видео)

Давление паров ртути в зависимости от температуры выражается уравнением

6. Фазовое равновесие в однокомпонентных системах

Условием равновесия между двумя фазами является равенство давления, температуры и химических потенциалов (мольных энергий Гиббса) в обеих фазах. Если температура изменяется при постоянном давлении или давление изменяется при постоянной температуре, то равновесие нарушается и одна из фаз исчезает. Изменение химических потенциалов фаз при этом можно рассчитать по уравнениям:

, (6.1)

, (6.2)

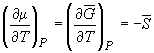
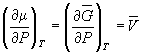
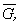
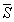
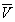
где и – мольные энергия Гиббса, энтропия и объем.

Условие сосуществования двух фаз при одновременном изменении давления P и температуры T описывается уравнением Клапейрона:

, (6.3)

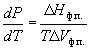
где H_ф.п. – мольная энтальпия равновесного фазового перехода (плавление, испарение, возгонка, переход между модификациями), V_ф.п. – разность мольных объемов фаз, находящихся в равновесии.

В случаях испарения и возгонки уравнение (6.3) можно упростить, считая, что мольным объемом конденсированной фазы (жидкости или твердого тела) V_к.ф. по сравнению с мольным объемом пара V_пар можно пренебречь и что пар подчиняется уравнению состояния идеального газа. Подставляя (V_пар – V_к.ф.) V_пар и V_пар = RT/P, получаем уравнение Клаузиуса-Клапейрона:

(6.4)

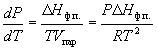
или после преобразования

. (6.5)

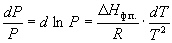
Интегрирование в предположении, что H_ф.п. не зависит от температуры (что справедливо в узких интервалах температур), дает

(6.6)

(6.7)

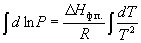
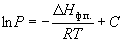
где C – константа интегрирования. Следовательно, зависимость lnP от 1/Т должна быть линейной, а наклон прямой равен – H_ф.п./R.

(6.8)

(6.9)

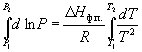
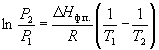
По этому уравнению можно рассчитать энтальпию испарения или возгонки, исходя из значений давления пара при двух разных температурах.

Мольные энтальпии возгонки, плавления и испарения при данной температуре связаны соотношением

_возгH = _плH + _испH (6.10)

Энтальпию испарения жидкости можно приближенно оценить по правилу Трутона, согласно которому мольная энтропия испарения в нормальной точке кипения (при 1 атм) приблизительно постоянна:

_испS = 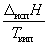88 Дж . моль –1 . К –1 (6.11)

Правило хорошо выполняется для неполярных жидкостей.

Зависимость энтальпии фазового перехода от температуры можно рассчитать по закону Кирхгофа:

(6.12)

(6.13)

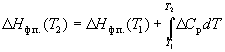
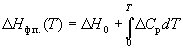
где C_p – разность теплоемкостей фаз, находящихся в равновесии, H₀ – константа интегрирования, определяемая из известных значений H_ф.п. и C_p. Для небольших интервалов температуры можно считать, что C_p = const. В этом случае из уравнения (6.13) получаем:

H_ф.п. (T) = H₀ + T C_p. (6.14)

Подставляя уравнение (6.14) в уравнение (6.7), получаем:

, (6.15)

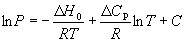
в котором С определяют из известных значений P, H₀ и C_p.

Пример 6-1. Рассчитать изменение давления, необходимое для изменения температуры плавления льда на 1 o C. При 0 o C энтальпия плавления льда равна 333.5 Дж . г –1 , удельные объемы жидкой воды и льда равны V_ж. = 1.0002 см 3 . г –1 и V_тв. = 1.0908 см 3 . г –1 .

Решение. Изменение объема при плавлении льда равно

V_ж. – V_тв. = 1.0002 – 1.0908 = –0.0906 см 3 . г –1 = –9.06 10 –8 м 3 . г –1 .

= –1.348 10 7 (Па . К –1 ) = –133 атм . К –1 .

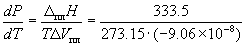
Таким образом, при повышении давления на 133 атм температура плавления льда понижается на 1 градус. Знак «минус» показывает, что при повышении давления температура плавления понижается.

Ответ. P = 133 атм.

Пример 6-2. Рассчитать давление пара жидкого брома при 25 o C. _fG o газообразного брома равна 3.110 кДж . моль –1 .

Решение. _испG o брома равно _fG o [Br₂ (г)] = 3110 Дж . моль –1 .

_испG o = 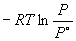, откуда P = 0.2852 атм.

Ответ. P = 0.2852 атм.

Пример 6-3. Рассчитать давление, при котором графит и алмаз находятся в равновесии при 25 o C. _fG o алмаза равна 2.900 кДж . моль –1 . Считать плотности графита и алмаза равными 2.25 и 3.51 г . см –3 соответственно и не зависящими от давления.

Решение. Изменение объема при переходе от графита к алмазу равно

V = 12 . 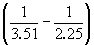10 –6 = –1.91 10 –6 м 3 . моль –1

При начальном давлении P₁ разность мольных энергий Гиббса G₁ = 2900 Дж . моль –1 , а при конечном давлении P₂ разность G₂ =0.

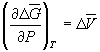
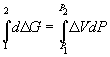
Поскольку , то = G₂ – G₁ = V(P₂ – P₁).

Отсюда P₂ = 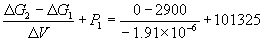= 1.52 10 9 Па = 1.5 10 4 атм.

Ответ. P = 1.5 10 4 атм.

Пример 6-4. Температура кипения бензола при давлении 1 атм равна 80.1 o C. Оценить давление пара бензола при 25 o C.

Решение. Давление пара бензола при T₁ = 353.3 K равно P₁ = 1 атм. По правилу Трутона _испH = 88 . 353.3 = 31.1 кДж . моль –1 . Подставим эти данные в уравнение (6.9). Получим:

, откуда P₂ = 0.141 атм.

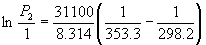
ЗАДАЧИ

Рассчитать давление, при котором две формы CaCO₃ – кальцит и арагонит – находятся в равновесии при 25 o C. _fG o кальцита и арагонита при 25 o C равны –1128.79 и –1127.75 кДж . моль –1 соответственно. Считать, что плотности кальцита и арагонита равны 2.71 и 2.93 г . см –3 соответственно и не зависят от давления.
Рассчитать температуру, при которой две формы CaCO₃ – кальцит и арагонит – находятся в равновесии при давлении 1 атм. При 25 o C _fG o кальцита и арагонита равны –1128.79 и –1127.75 кДж . моль –1 соответственно, _fH o равны–1206.92 и –1207.13 кДж . моль –1 соответственно. Считать, что C_P = 0.
_fG o жидкой и газообразной воды при 25 o C равны –237.129 и –228.572 кДж . моль –1 соответственно. Рассчитать давление пара воды при 25 o C.
Плотности жидкого и твердого олова при температуре плавления (231.9 o C) равны 6.980 г . см –3 и 7.184 г . см –3 соответственно. Энтальпия плавления олова равна 1.690 ккал . моль –1 . Определить температуру плавления олова под давлением 500 атм. Молярная масса олова равна 118.7 г . моль –1 .
При замерзании бензола (5.5 o C) его плотность изменяется от 0.879 г . см –3 до 0.891 г . см –3 . Энтальпия плавления равна 10.59 кДж . моль –1 . Определить температуру плавления бензола при давлении 1000 атм.
Плотности жидкой и твердой ртути при температуре плавления
(–38.87 o C) равны 13.690 и 14.193 г . см –3 соответственно. Энтальпия плавления ртути равна 2.33 кал . г –1 . Определить температуру плавления ртути при давлении 3000 атм.
Температура кипения жидкого метанола равна 34.7 o C при давлении 200 мм рт. ст. и 49.9 o C при давлении 400 мм рт. ст. Найти температуру кипения метанола при нормальном давлении.
Давление пара диэтилового эфира при 10 o C равно 286.8 мм рт. ст., а при 20 o C – 432.8 мм рт. ст. Определить мольную энтальпию испарения и нормальную температуру кипения эфира.
Давление пара дихлорметана при 24.1 o C равно 400 Торр, а его энтальпия испарения равна 28.7 кДж . моль –1 . Рассчитать температуру, при которой давление пара будет равно 500 Торр.
Давление пара твердого CO₂ равно 133 Па при –134.3 o C и 2660 Па при –114.4 o C. Рассчитать энтальпию возгонки.
Давление пара (Торр) жидкости в интервале температур 200 – 260 K описывается уравнением:

ln p = 16.255 – 2501.8 / T.

Рассчитать энтальпию испарения и нормальную точку кипения жидкости.

Давление пара (Торр) жидкого бензола C₆H₆ между 10 o C и 80 o C описывается уравнением:

lg p = 7.960 – 1780 / T.
Рассчитать энтальпию испарения и нормальную точку кипения бензола.

Давление пара жидкого нафталина C₁₀H₈ равно 10 Торр при 85.8 o C и 40 Торр при 119.3 o C. Определить энтальпию испарения, нормальную точку кипения и энтропию испарения в нормальной точке кипения.

Нормальная точка кипения гексана равна 69.0єC. Оценить а) мольную энтальпию испарения и б) давление пара гексана при 25єC и 60єC.

При 0 o C энтальпии испарения и плавления воды равны 595 и 79.7 кал . г –1 соответственно. Давление пара воды при 0 o C равно 4.58 мм рт. ст. Рассчитать давление пара льда при –15 o C, считая, что изменение энтальпии не зависит от температуры.

Рассчитать температуру кипения воды на вершине Эвереста (высота 8850 м). Энтальпию испарения воды считать равной 40.67 кДж . моль –1 . Для расчета атмосферного давления на вершине воспользоваться барометрической формулой.

Уксусная кислота имеет следующие давления насыщенного пара:

403P, мм. рт. ст.

Определить молярную массу уксусной кислоты в паре, если известно, что «_испH = 24.35 кДж . моль –1 .

Давление пара (в мм рт. ст.) твердого и жидкого SO₂ выражается уравнениями

Видео:Урок 124 (осн). Зависимость температуры кипения жидкости от давленияСкачать

Давление паров ртути в зависимости от температуры выражается уравнением

110. (1/2-00).* Зависимость температуры плавления Sn от давления (в бар) передается выражением t(&3176;С) = 231,8 + 0,0032(P–1). Найти плотность твердого олова ρ тв , учитывая, что Q пл = 7,2 кДж/моль и ρ ж = 6,988 г/см 3 . Молекулярная масса олова 119.
Решение

111. (1/2-05). При 1 бар, 125 о С твердые модификации селен (1) и селен (2) равновесно сосуществуют. Энтропии Se(1) и Se(2) равны соответственно 31 и 42 Дж/К . моль. Полагая теплоемкости этих двух фаз равными, вычислить изменения энергии Гиббса при переходе Se(1) → Se(2) при 25° С. Какая фаза селена устойчива при 25° С: Se(1) или Se(2)?

112. (2/2-06). При давлении 1 атм довели температуру 1 моля кристаллического нафталина до температуры плавления. Какое количество тепла необходимо подвести извне для перевода полученного нафталина в жидкое состояние? Известно, что температура плавления нафталина зависит от давления ( P , атм) следующим образом:

t° C = 79,8 + 0,0373· P + 1,9·10 –6 ·P 2 .

Разность мольных объемов жидкого и твердого нафталина равна
Δ V = 18,69 см 3 /моль.

113. (3/2-97). Давление насыщенного пара (бар) над жидким йодом описывается температурной зависимостью

lgP = –3212/T – 5,193 lgT + 23,705.

Найти теплоемкость газообразного йода, если теплоемкость жидкого йода при температуре кипения 114 °С равна 80,26 Дж/моль·К.

114. (3/Э-01). Давление пара ртути выражается уравнением

lg(Р/торр) = –3328/T – 0,848 lgT + 10,53.

Определить теплоту испарения ртути при температуре кипения (356,66 °С) и удельную теплоемкость жидкой ртути.

115. (1/2-08). Зависимости давления насыщенного пара для твердой и жидкой муравьиной кислоты (в мм рт. ст.) от температуры выражаются уравнениями: lg ⁡ P т в = 12,486 − 3160 T , lg ⁡ P ж = 7,484 − 1860 T . MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaacEgacaWGqbWaaSbaaSqaaiaadkebcaWGYqaabeaakiabg2da9iaaigdacaaIYaGaaiilaiaaisdacaaI4aGaaGOnaiabgkHiTmaalaaabaGaaG4maiaaigdacaaI2aGaaGimaaqaaiaadsfaaaGaaiilaiaaywW7ciGGSbGaai4zaiaadcfadaWgaaWcbaGaamOneaqabaGccqGH9aqpcaaI3aGaaiilaiaaisdacaaI4aGaaGinaiabgkHiTmaalaaabaGaaGymaiaaiIdacaaI2aGaaGimaaqaaiaadsfaaaGaaiOlaaaa@54A9@

Рассчитать теплоты испарения, сублимации и плавления. Рассчитать энтропии испарения и сублимации в нормальных точках испарения и сублимации. Рассчитать координаты тройной точки.

116. (3/Э-08). Замечено, что в диапазоне температур от 10 ° С до 25 ° С давление насыщенных паров воды приблизительно следует правилу: «сколько градусов – столько мм рт. ст.». Оцените теплоту испарения воды и температуру кипения воды при атмосферном давлении.

117. (2/2-03). По мотивам книги Роберта Хайнлайна «Фермер в небе»: «Во время полета давление было десять фунтов; теперь капитан Хэтти спустила его до трех, то есть до нормального давления на Ганимеде. Ясно, что трех фунтов кислорода вполне достаточно для жизни; на Земле его, кстати, не больше – остальные двенадцать фунтов приходятся на долю азота. Но когда давление падает так внезапно, вы начинаете судорожно хватать ртом воздух….».
Ганимед – спутник Юпитера, сила тяжести

1/3 земной.
Удастся ли колонистам планеты Ганимед сварить куриное яйцо? Если нет, предложите свой способ, используя подручные средства. Ответ обоснуйте. Температура денатурации белка 62 °С.

Δ f H 298 o MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdq0aaSbaaSqaaiaadAgaaeqaaOGaamisamaaDaaaleaacaaIYaGaaGyoaiaaiIdaaeaacaWGVbaaaaaa@3CA3@ ,
кДж/моль

S 298 o MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaDaaaleaacaaIYaGaaGyoaiaaiIdaaeaacaWGVbaaaaaa@3A27@ ,
, Дж/моль·К

C p , 298 o MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaDaaaleaacaWGWbGaaiilaiaaykW7caaIYaGaaGyoaiaaiIdaaeaacaWGVbaaaaaa@3D47@ ,
, Дж/моль·К

118. (2/2-04). Можно ли высушить белье при температуре –10 о С в зимнем приморском городе на открытом воздухе? В этом городе при –10° С влажность воздуха, приведенная в виде давления насыщенных паров воды, колеблется в интервале 2,00 – 2,10 торр. Известно, что:

а) белье всегда «замерзает» при указанной температуре;

б) изменение энергии Гиббса для процесса Н 2 О(ж., –10 °С) → Н 2 О(тв., –10 о С) составляет –212,4 Дж/моль;

в) при –10 °С равновесное давление насыщенных паров над жидкой водой равно 2,149 торр.

119. (1/2-01). Сколько тонн воды может испариться с 1 км 2 влажной земли в ясный безветренный летний день, если считать, что лимитирующий фактор – поступление солнечного тепла, которое составляет в среднем 4,18 Дж/(с· см 2 ) в течение 8-часового дня?

Какой минимальный объем воздуха нужен, чтобы вместить это количество воды при температуре почвы и воздуха 25 °С? Давление насыщенного пара воды при 11,3 °С равно 10 торр, а теплота испарения 2433 Дж/г.

120. (3/Э-06). Коньки, заточенные «под желобок», имеют толщину острия лезвия около 50 мкм.

Оцените температуру плавления льда под спортсменом весом 70 кг на коньках длиной 30 см. Плотность воды 1 г/см 3 , льда – 0,9 г/см 3 . Молекулярная масса воды 18 г/моль .

121. (6/2-01).Оцените температуру, при которой максимальна плотность насыщенных паров серы Т кип (S) = 444.6 °C; T кр (S) = 1040 °C; Δ исп H = 2200 кал/моль. Считать, что Δ исп H не зависит от температуры, а вещество в газовой фазе подчиняется уравнению состояния идеального газа.

122. (5/Э-97). Состояние воды в широком диапазоне температур и давлений достаточно хорошо описывается уравнением Ван-дер-Ваальса:

p = R T V − b − a V 2 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabg2da9maalaaabaGaamOuaiaadsfaaeaacaWGwbGaeyOeI0IaamOyaaaacqGHsisldaWcaaqaaiaadggaaeaacaWGwbWaaWbaaSqabeaacaaIYaaaaaaaaaa@3FFE@ , a = 5,46·10 –6 м 6 ·бар·моль –2 , b = 31·10 –6 м 3 ·моль –1 .

Оценить по этим данным параметры критического состояния воды (P K , T K , V K ). Какой термодинамической вариантностью характеризуется эта точка?

Видео:Физика Один грамм паров ртути и один грамм гелия имеют одинаковую температуру. Какой из газов имеетСкачать

Примеры решения типовых задач. DHисп = lисп×МHg = 283,2 Дж/г ×200,6 г/моль =

1. Температура кипения ртути при нормальном атмосферном давлении равна 357°С. Теплота испарения равна 283,2 Дж/г. Определить изменение давления пара ртути при изменении температуры на 1°С вблизи температуры кипения ртути при нормальном атмосферном давлении.

Т = 357 + 273 = 630 К

2. Давление паров воды при 97°С равно 90919,9 Па, а при 103°С – 112651,8 Па. Определить давление паров воды при 110°С.

3. Удельная теплота плавления нафталина при t_пл = 79,9 о С равна 149,25 Дж/г. Разность удельных объемов в жидком и твердом состояниях (DV) при 79,9°С равна 0,146 см 3 /г. Определить изменение Т_пл нафталина при увеличении давления в 100 раз по сравнению с атмосферным.

;

Так как давление дано в Па, а DH_пл в Дж/г то DV должно быть выражено в м 3 /кг, а энтальпия плавления в Дж/кг.

3,452×10 –7 К/Па

DТ_пл = 3,452×10 –7 ×(101,3×10 2 ×10 3 – 101,3×10 3 ) = 3,46 К.

Задачи для самостоятельного решения

1. Энтальпия испарения воды при температуре кипения при нормальном атмосферном давлении равна 2258,4 Дж/г. Определить изменение давления пара воды при изменении температуры на 1°С вблизи температуры кипения.

2. Температура кипения ртути при нормальном атмосферном давлении равна 357°С. Изменение давления пара ртути при изменении температуры на 1°С вблизи температуры кипения при нормальном атмосферном давлении равно 1,744×10 3 Па. Вычислить энтальпию испарения ртути в Дж/г.

3. Давление паров воды при 95° и 97°С соответственно равно 84513 и 90920 Па. Вычислить энтальпию испарения воды (Дж/моль) и количество теплоты, необходимое для испарения 100 кг воды.

(Ответ: 41,36 кДж/моль; 229,8 МДж)

4. Давление паров иода при 90°С равно 3572,4 Па, а при 100°С – 6065,15 Па. Определить давление паров иода при температуре 115 о С.

5. Температура плавления (°С) нафталина в зависимости от давления (Па) выражается уравнением

Разность удельных объемов в жидком и твердом состоянии равна 0,146×10 –3 м 3 /кг. Рассчитать энтальпию плавления при давлении 50,66×10 5 Па.

6. Зависимость давления p пара никотина C₁₀H₁₄N₂ от температуры t имеет вид (1 атм =760 мм рт. ст.)

t, °С

p, мм рт. ст.

По графику зависимости lnp от 1/T рассчитайте энтальпию испарения в указанном интервале температур.

(Ответ: 41,29 Дж/моль)

Фазовые равновесия в двухкомпонентных системах, перегонка

Основные уравнения

Если система состоит из двух компонентов, а на состояние равновесия влияют такие внешние факторы, как температура и давление, то правило фаз Гиббса имеет вид:

С = 2 – Ф + 2 = 4 – Ф.

(145)

При С_min = 0 число фаз Ф = 4. Следовательно, в двухкомпонентной системе число фаз, одновременно находящихся в равновесии, не может быть больше четырех (ж, п, А_т, В_т). Максимальное число степеней свободы С_max при Ф_min = 1 равно 3 (давление, температура и концентрации х₁ одного из компонентов). При выражении концентрации в процентах или долях x₁ = 1 – х₂ и при выбранных параметрах (р, Т, х₁ = 1 – х₂) состояние двухкомпонентной системы можно изобразить с помощью трехмерной диаграммы. Часто состояние двухкомпонентных систем изучают при p = const или T = const. В этом случае уравнение (145) приобретает вид

С = 2 – Ф + 1 = 3 – Ф,

(146)

а диаграмма, построенная в координатах «температура – состав» или «давление – состав», будет плоской.

Равновесие «твердое вещество – жидкость».
Фазовая диаграмма системы с простой эвтектикой

Равновесия в системах «твердое вещество – жидкость» встречаются при изучении различных металлических сплавов, силикатов, водных растворов солей, систем, состоящих из органических соединений.

Особое значение имеют исследования зависимостей температур начала и конца кристаллизации твердых веществ от состава системы. Графики, выражающие эту зависимость, называются фазовыми диаграммамиили диаграммами плавкости.

Диаграммы плавкости строятся на основании результатов термического анализа, который заключается в наблюдении за скоростью охлаждения расплавленных чистых веществ и их смесей.

Диаграммы такого типа отвечают бинарным системам, в которых вещества неограниченно смешиваются в жидком состоянии, образуя гомогенный раствор и практически не растворяются в твердом состоянии, образуя гетерогенную систему из твердых фаз.

Рассмотрим построение и анализ такой диаграммы на примере системы из веществ А и В.

Рис. 41. Фазовая диаграмма системы

с простой эвтектикой

Линия – линия ликвидуса, линия MN – линия солидуса, они разбивают диаграмму на четыре области:

· область I –жидкий расплав;

· область II – гетерогенная система, состоящая из кристаллов вещества А и жидкого расплава переменного состава;

· область III – гетерогенная система, состоящая из кристаллов вещества В и жидкого расплава переменного состава;

· область IV – гетерогенная система, состоящая из смеси кристаллов А и В.

Каждая точка на диаграмме называется фигуративной и соответствует одному строго определенному состоянию системы в зависимости от того, где эта точка лежит.

Чтобы найти состав сосуществующих фаз, надо через фигуративную точку провести горизонталь до пересечения с граничными линиями, из точки пересечения с одной граничной линией опустить перпендикуляр на ось состава – это даст состав одной фазы, из другой – состав другой фазы. Например, для того чтобы найти состав сосуществующих фаз в точке r, проведем горизонталь до пересечения с линией ликвидус и опустим перпендикуляр из точки пересечения (S), определим массовую долю В в расплаве (ω_В), второй конец горизонтали пересекается с левой осью ординат, соответствующей чистому веществу А, находящемуся при температуре t_r, ниже температуры его плавления (t 0 _А), следовательно вещество А находится в виде кристаллов.

Диаграмма плавкости позволяет определить не только число фаз и их состав, но и относительные массы фаз, с помощью правила рычага:

Давление паров ртути в зависимости от температуры выражается уравнением

(147)

где g_ж – масса расплава, г; g_тв – масса кристаллов, г.

Отрезки t_rr и rS измеряются на диаграмме в сантиметрах или миллиметрах (рис. 41).

Одним из методов построения диаграмм состояния является метод термического анализа, который заключается в построении кривых охлаждения. Рассмотрим пример: расплавим чистое вещество А и будем его равномерно охлаждать, измеряя температуру. Нанеся эти данные на график, получим кривую охлаждения(рис. 42). Кривая охлаждения любого чистого вещества (однокомпонентная система K = 1) будет состоять из трех участков ab, bc, cd.

Рис. 42. Кривая охлаждения чистого вещества

Изломы на кривых охлаждения (графиках в координатах «температура – время») свидетельствуют об изменении числа фаз в системе (рис. 42 и 43).

Участок ab соответствует охлаждению чистого жидкого вещества А, так как охлаждение ведется равномерно, то он соответствует прямой линии, наклоненной под определенным углом. Число степеней свободы (С) в такой системе рассчитываем по правилу фаз Гиббса: С = K – Ф + n; n = 1, а С = 1 – 1 + 1 = 1 (то есть температура понижается, но при этом сохраняется жидкая фаза).

Когда в жидкости появятся первые кристаллы, система станет двухфазной (твердая и жидкая фазы), а число степеней свободы становится равным нулю: С = 1 – 2 + 1 = 0. Следовательно, при охлаждении однокомпонентной системы (чистого вещества) температура не может изменяться, на кривой охлаждения появляется горизонтальный участок – участок bc.

Охлаждение системы компенсируется теплотой, которая выделяется при кристаллизации. Таким образом, температура горизонтального участка – это температура кристаллизации чистого вещества А.

Когда вся жидкость закристаллизуется, в системе останется одна фаза – твердая, число степеней свободы снова станет равно 1: С = 1 – 1 + 1 = 1.

Такая же кривая охлаждения соответствует и чистому веществу В, только горизонтальный участок будет наблюдаться при другой температуре (при температуре плавления В).

Теперь к твердому веществу А добавим 10% вещества В, смесь расплавим, получим расплав и будем его охлаждать. По результатам охлаждения построим кривую охлаждения (рис. 43), она состоит из четырех участков: mn, nf, fk и kl.

Рис. 43. Кривая охлаждения смеси

Участок mn соответствует охлаждению расплава:

Как только в расплаве появятся кристаллы вещества А (С = 2 – 2 + 1 = 1), температура системы будет понижаться уже медленнее из-за того, что при образовании кристаллов выделяется теплота, замедляющая охлаждение, на кривой появится изгиб (точка n), который будет указывать температуру начала кристаллизации (T_n). В соответствии с законом Рауля наблюдается понижение температуры замерзания раствора (температура начала выпадения кристаллов) по сравнению с температурой замерзания чистого жидкого вещества, поэтому T_n