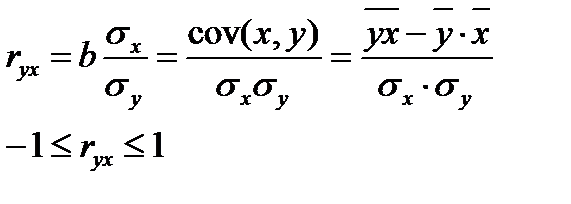Рис. 4.1. Интерпретация параметров модели
Коэффициенты корреляции и детерминации в линейной модели парной регрессии. Если все точки лежат на построенной прямой, то регрессия Y на Х «идеально» объясняет поведение зависимой переменной. Обычно поведение Y лишь частично объясняется влиянием переменной Х.
Рис. 4.2. Диаграмма Венна
Линейный коэффициент парной корреляции:
Если b>0, то ryx>0; если b 2 – остаточная дисперсия на одну степень свободы;
t – случайная величина, имеющая распределение Стьюдента с заданной вероятностью.
Вопросы и задания для самоконтроля
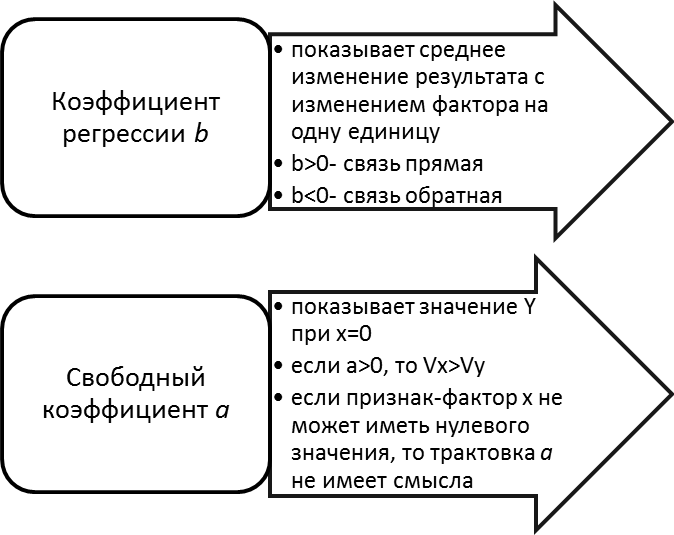
1. Каков экономический смысл коэффициента регрессии?
2. Какой смысл может иметь свободный коэффициент уравнения регрессии?
3. Какова связь между линейным коэффициентом корреляции и коэффициентом регрессии в линейной модели парной регрессии?
4. Каков статистический смысл коэффициента детерминации?
5. Как записывается баланс для сумм квадратов отклонений результативного признака?
6. Что происходит, когда общая СКО равна остаточной? В каком случае общая СКО равна факторной?
7. Что такое число степеней свободы? Чему равны числа степеней свободы для различных СКО в парной регрессии?
8. Как используется F-статистика в регрессионном анализе?
9. Как F-статистика связана с коэффициентом детерминации в парной регрессии?
10. Как рассчитать критерий Стьюдента для коэффициента регрессии в линейной модели парной регрессии?
11. В чем суть предсказания индивидуальных значений зависимой переменной?
Задача 1. Пусть имеется следующая модель парной регрессии, построенная по 20 наблюдениям: 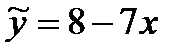
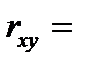
Задание: построить доверительный интервал для коэффициента регрессии в этой модели с вероятностями 0,9 и 0,95.
Задача 2. Анализируется зависимость между доходами горожан (X), имеющими индивидуальные домовладения, и рыночной стоимостью их домов (Y). По случайной выборке из 120 горожан данной категории получены результаты:

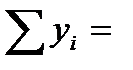
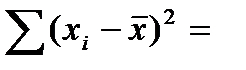
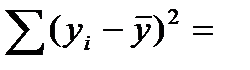

Задание: найти оценку коэффициента регрессии 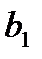
Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Качество регрессионной модели. Нелинейная регрессия
Значимость уравнения регрессии еще не означает, что выбранная модель достаточно правильно (адекватно) описывает исследуемое экономическое явление. Применение неадекватной модели для целей анализа и прогнозирования может приводить к неоправданно большим ошибкам. Если модель адекватна, то остатки регрессии представляют собой независимые нормально распределенные случайные величины с одинаковой дисперсией. В случае неадекватности модели остатки содержат также и систематическую составляющую, а закон их распределения отличается от нормального. Проверка адекватности регрессионной модели рассматривается в § 3.8.
Обычно в начале исследуется линейная модель, для которой после оценки параметров и проверки значимости уравнения регрессии определяется коэффициент детерминации и оценивается точность.
Коэффициент детерминации R 2 рассчитывается по формуле
 . . | (2.19) |
Его значение показывает долю вариации результата Y, обусловленную вариацией фактора X. К примеру, если R 2 =0,856, то это означает, что 85,6 % вариации результата Y вызвано вариацией фактора X, а соответственно 14,4 % ( 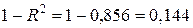
Заметим, что для линейной парной модели коэффициент детерминации равен квадрату коэффициента корреляции: 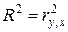
 , , | (2.20) |
где Sy — стандартное отклонение зависимой переменной Y в исходных данных.
Коэффициент детерминации и F–статистика Фишера (см. § 2.3) связаны между собой соотношением
 , , | (2.21) |
где n — число наблюдений; m — число оцениваемых параметров регрессионной модели, включая свободный коэффициент b0.
В случае парной линейной регрессии m=2 и
 . . | (2.22) |
Точность модели, т.е. близость линии регрессии к фактическим данным,характеризует средняя относительная ошибка аппроксимации
 . . | (2.23) |
Если Еотн не превышает 10 %, то считается, что модель имеет высокую точность, при 

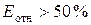
Средняя относительная ошибка аппроксимации Еотн связана со стандартной ошибкой регрессии Sрег приближенным соотношением
 . . | (2.24) |
Расхождение между формулами (2.23) и (2.24) обычно незначительное, особенно при достаточно большом объеме наблюдений ( 
После анализа качества линейной модели переходят к исследованию нелинейных моделей, коэффициент детерминации и средняя относительная ошибка аппроксимации которых, определяются по тем же самым формулам и имеют тот же смысл, что и для линейной модели. Наиболее часто на практике используются нелинейные модели, приведенные в табл. 2.2.
Значимость нелинейного уравнения регрессии проверяется по F‑критерию Фишера. Лучшей считается модель, имеющая наибольший коэффициент детерминации R 2 . При незначительных расхождениях в значениях R 2 предпочтение отдается более простой модели. Если модель предполагается использовать для целей анализа, то ее параметры должны иметь содержательную экономическую интерпретацию. Интерпретация параметров степенной, показательной и логарифмической регрессий рассматривается в приведенных ниже примерах.
| Таблица | 2.2 |
| Часто используемые на практике нелинейные модели |
| Форма связи | Модель | Уравнение регрессии |
| 1. Степенная | 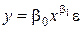 | 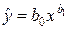 |
| 2. Показательная |  | 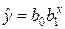 |
| 3. Экспоненциальная (другой вид показательной связи) |  |  |
| 4. Логарифмическая | 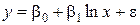 |  |
| 5. Гиперболическая |  |  |
| 6. Полиноминальная разных степеней (q — степень полинома) |  |  |
Решение типовых задач
Пример 2.1
По десяти однородным предприятиям имеется информация, характеризующая зависимость объема выпускаемой продукции (результативная переменная Y, млн. руб.) от объема капиталовложений (фактор X, млн. руб.):
| Предприятие | А | Б | В | Г | Д | Е | Ж | З | И | К |
| Y | ||||||||||
| X |
1. Рассчитать парный коэффициент корреляции между переменными Y и X и проверить его статистическую значимость (уровень значимости a=0,05).
2. Найти параметры уравнения линейной регрессии Y по X и дать их экономическую интерпретацию.
3. Вычислить коэффициент детерминации R 2 и пояснить его смысл.
4. Проверить статистическую значимость уравнения регрессии по F-критерию Фишера (a=0,05).
5. Определить стандартную ошибку регрессии и оценить точность модели с помощью средней относительной ошибки аппроксимации.
6. Построитьдоверительные интервалы для истинных параметров b0 и b1 регрессионной модели и проверить статистическую значимость коэффициентов уравнения регрессии по t-критерию Стьюдента (a=0,05).
7. Спрогнозировать с доверительной вероятностью 0,9 значение показателя Y, если прогнозное значения фактора Х составит 80 % от максимального значения в исходных данных.
8. Изобразить графически результаты моделирования и прогнозирования.
1. Для определения парного коэффициента корреляции ry,x между переменными Y и X в EXCEL может быть использована любая из встроенных функций «КОРРЕЛ» или «ПИРСОН». Использование встроенных функций EXCEL рассмотрено в § 5.4.
Коэффициент корреляции имеет значение

Критическое значение коэффициента корреляции для уровня значимости a=0,05 и числа степеней свободы 
2. Линейная модель парной регрессии Y по X и уравнение регрессии соответственно имеют вид:


Коэффициенты уравнения регрессии определяем с помощью встроенных функций «ОТРЕЗОК» и «НАКЛОН» соответственно. Они имеют значения:


Окончательно уравнение регрессии —
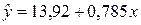
Значение свободного коэффициента b0 показывает, что при нулевом объеме капиталовложений X объем выпускаемой продукции Y будет составлять в среднем 13,92 млн. руб. Значение углового коэффициента b1=0,785 показывает, что при увеличении объема капиталовложений на 1 млн. руб. объем выпускаемой продукции возрастает в среднем на 0,785 млн. руб.
3. Коэффициент детерминации R 2 парной линейной регрессии определяется с помощью встроенной функции EXCEL «КВПИРСОН». Получим:

Значение R 2 показывает, что линейная модель объясняет 86,9 % вариации Y. Другими словами, 86,9 % вариации объема выпускаемой продукции Y обусловлена вариацией объема капиталовложений X.
4. Для проверки статистической значимости уравнения регрессии F‑статистику Фишера определимчерез коэффициент детерминации по формуле (2.22):
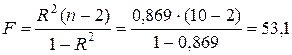
Табличное значение F-критерия Фишера для уровня значимости a=0,05 и чисел степеней свободы числителя (регрессии) 

5. Стандартная ошибка линейной парной регрессии Sрег (см. § 2.2) определяется с помощью встроенной функции EXCEL «СТОШYX». Имеем:

Среднюю относительную ошибку аппроксимации Еотн рассчитаем по приближенной формуле
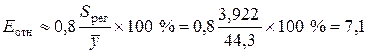
где 
Значение Еотн показывает, что предсказанные уравнением регрессии значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 7,1 %. Так как средняя относительная ошибка аппроксимации меньше 10 %, то это свидетельствует о высокой точности линейной модели.
6. Для определения интервальных оценок истинных параметров b0 и b1 регрессионной модели рассчитаем стандартные ошибки коэффициентов уравнения регрессии:


где 

Доверительный интервал, «накрывающий» с заданной надежностью 0,95 неизвестное значение параметра b0 модели, имеет вид:

где tтаб=2,306 — табличное значение t-критерия Стьюдента для уровня значимости a=0,05 и числа степеней свободы остатка линейной парной регрессии 
Таким образом, с доверительной вероятностью 95 % истинное значение параметра b0 будет находиться в интервале от 3,89 до 23,95 млн. руб. Так как нижняя и верхняя границы доверительного интервала имеют одинаковый знак, то коэффициент b0 уравнения регрессии признается статистически значимым на уровне значимости a=0,05.
Доверительный интервал для параметра b1 модели имеет вид:
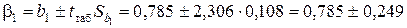
Это означает, что при увеличении объема капиталовложений X на 1 млн. руб. объем выпускаемой продукции Y с вероятностью 95 % возрастает в среднем на величину, заключенную в интервале от 0,536 до 1,034 млн. руб. Один и тот же знак доверительных границ свидетельствует о статистической значимости коэффициента b1 и уравнения регрессии в целом на уровне a=0,05.
7. Спрогнозируем объем выпускаемой продукции Y, если прогнозное значение x0 объема капиталовложений X составит 80 % от своего максимального значения в исходных данных xmax=59 млн. руб.:

Среднее прогнозируемое значение объема выпускаемой продукции (точечный прогноз) равно

Точечный прогноз можно рассчитать и с помощью встроенной функции «ПРЕДСКАЗ».
Стандартная ошибка прогноза фактического значенияобъема выпускаемой продукции y0 рассчитывается по формуле

где 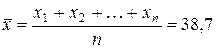
Интервальный прогноз фактического значения объема выпускаемой продукции y0 с надежностью g=0,9 (уровень значимости a=0,1) имеет вид:
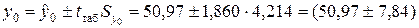
где tтаб=1,860 — табличное значение t-критерия Стьюдента при уровне значимости a=0,1 и числе степеней свободы 
Объем выпускаемой продукции с вероятностью 90 % будет находиться в интервале от 43,13 до 58,81 млн. руб.
8. График, на котором изображены фактические и предсказанные уравнением регрессии значения Y, строим с помощью надстройки «Мастер диаграмм» EXCEL (рис. 2.5). Данная надстройка позволяет построить линии нескольких видов регрессии (линейной, степенной, логарифмической, экспоненциальной и полиноминальной), определить их уравнение и коэффициент детерминации. Использование «Мастера диаграмм» рассмотрено в § 5.1.
рис. 2.5. Линия линейной парной регрессии и точки прогноза
Пример 2.2
Используя исходные данные предыдущего примера, выполнить следующие действия:
1. С помощью табличного процессора EXCEL построить уравнения линейной, логарифмической, степенной и показательной регрессий Y по X. Для указанных регрессий:
· привести графики их линий;
· дать экономическую интерпретацию параметрам уравнений;
· найти коэффициенты детерминации;
· проверить статистическую значимость уравнений по F-критерию Фишера;
· оценить точность моделей с помощью средней относительной ошибки аппроксимации.
2. Сравнить построенные модели между собой и выбрать лучшую из них для целей анализа и прогнозирования.
1. Линейную, степенную, логарифмическую и показательную регрессии строим с помощью «Мастера диаграмм» EXCEL. Линейная и степенная регрессии показаны на рис. 2.6, логарифмическая и показательная — на рис. 2.7. На графиках приводятся не только линии регрессии, но также их уравнения и коэффициенты детерминации (см. § 5.1).
рис. 2.6. Линии линейной и степенной регрессий
рис. 2.7. Линии логарифмической и показательной регрессий
Рассмотрим последовательно каждую модель.
1) Уравнение линейной регрессии имеет вид:
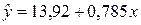
Угловой коэффициент b1=0,785 является показателем среднего абсолютного прироста. Его значение показывает, что при увеличении объема капиталовложений X на 1 млн. руб. объем выпускаемой продукции Y возрастает в среднем на 0,785 млн. руб.
Коэффициент детерминации R 2 =0,869 показывает, что линейная модель объясняет 89,8 % вариации объема выпускаемой продукции Y.
F-статистика Фишера линейной модели определяем через коэффициент детерминации R 2 по формуле
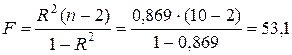
Табличное значение F-критерия Фишера для уровня значимости a=0,05 и чисел степеней свободы числителя (регрессии) 

Следует заметить, что табличное значение F-критерия Фишера одинаково как для линейной, так и для всех нелинейных моделей, которые здесь строятся (Fтаб=5,32).
Стандартная ошибка линейной регрессии рассчитывается по формуле

где 
Среднюю относительную ошибку аппроксимации определяем по приближенной формуле

где 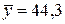
Предсказанные уравнением линейной регрессии значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 7,1 %.
2) Уравнение степенной регрессии выглядит следующим образом:

Показатель степени b1=0,721 является средним коэффициентом эластичности. Его значение показывает, что при увеличении объема капиталовложений X на 1 % объем выпускаемой продукции Y возрастает в среднем на 0,721 %.
Коэффициент детерминации R 2 =0,873 показывает, что степенная модель объясняет 87,3 % вариации объема выпускаемой продукции Y.
F-статистика степенной модели
также превышает табличное значение F-критерия Фишера (Fтаб=5,32), что указывает на статистическую значимость уравнения степенной регрессии.
Стандартную ошибку и среднюю относительную ошибку аппроксимации нелинейных регрессий будем определять по тем же самым формулам, что и для линейной модели. Для степенной регрессии они равны:


Предсказанные уравнением степенной регрессии значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 7,0 %.
3) Уравнение логарифмической регрессии имеет вид:

Значение параметра b1=29,9 показывает, что при увеличении объема капиталовложений X на 1 % объем выпускаемой продукции Y возрастает в среднем на 
Коэффициент детерминации R 2 =0,898 показывает, что логарифмическая модель объясняет 89,8 % вариации объема выпускаемой продукции Y.
F-статистика Фишера логарифмической модели равна
и превышает табличное значение F-критерия Фишера (Fтаб=5,32). Это свидетельствует о статистической значимости уравнения регрессии.
Стандартная ошибка логарифмической регрессии составляет

Средняя относительная ошибка аппроксимации имеет значение

Предсказанные уравнением логарифмической регрессии значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 6,2 %.
4) Уравнение показательной регрессии определяется через экспоненциальную регрессию:

где е=2,718… — основание натуральных логарифмов; 
Параметр b1=1,019 показательной регрессии 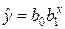
Заметим, что параметр b1 экспоненциальной регрессии 


Уравнения показательной и экспоненциальной регрессии являются эквивалентными.
Коэффициент детерминации R 2 =0,821 показывает, что показательная модель объясняет 82,1 % вариации объема выпускаемой продукции Y.
F-статистика показательной модели
превышает табличное значение F-критерия Фишера (Fтаб=5,32), что свидетельствует о статистической значимости уравнения регрессии.
Стандартная ошибка показательной регрессии

Средняя относительная ошибка аппроксимации

Предсказанные уравнением показательной регрессии значения объема выпускаемой продукции Y отличаются от фактических значений в среднем на 8,3 %.
2. Сравнивая между собой коэффициенты детерминации R 2 четырех моделей, можно придти к выводу, что лучшей из них является логарифмическая модель, так как она имеет самое большое значение R 2 . Эту модель и целесообразно использовать в качестве рабочей для анализа и прогнозирования изменения объема выпускаемой продукции Y в зависимости от изменения объема капиталовложений X.
Заметим, что при выборе лучшей модели из четырех рассмотренных для целей анализа параметр b1 должен иметь содержательную интерпретацию. Так, если бы переменные X и Y были относительными величинами и измерялись в процентах, то корректная интерпретация параметра b1 нелинейных моделей оказалась бы затруднительной. В этом случае для прогнозирования следовало бы выбрать модель с большим R 2 , а для целей анализа — линейную модель.
Пример 2.3
В магазине исследуется зависимость количества реализованных за день упаковок шампуня (Y, шт.) от цены одной упаковки (X, руб.). Имеется информация по одиннадцати наименованиям шампуня:
| Шампунь | А | Б | В | Г | Д | Е | Ж | З | И | К | Л |
| Y | |||||||||||
| X |
Выполнить те же самые действия, что и в предыдущем примере.
1. Линейную, степенную, логарифмическую и показательную регрессии строим с помощью «Мастера диаграмм» EXCEL. Линейная и степенная регрессии показаны на рис. 2.8, логарифмическая и показательная — на рис. 2.9.
Используя формулы предыдущего примера, рассчитаем для каждой модели коэффициент детерминации R 2 , F-статистику Фишера, стандартную ошибку регрессии Sрег и среднюю относительную ошибку аппроксимации Eотн ( 
рис. 2.8. Линии линейной и степенной регрессий
рис. 2.9. Линии логарифмической и показательной регрессий
| Таблица | 2.3 |
| Сводная таблица результатов моделирования |
| Модель | Уравнение регрессии | R 2 | F | Sрег, шт. | Eотн, % |
| 1. Линейная |  | 0,788 | 33,45 | 6,62 | 11,8 |
| 2. Степенная |  | 0,857 | 53,94 | 5,43 | 9,7 |
| 3. Логарифмическая |  | 0,834 | 45,22 | 5,86 | 10,4 |
| 4. Показательная (экспоненциальная) |  ( (  ) ) | 0,825 | 42,43 | 6,01 | 10,7 |
Очевидно, что между переменными X и Y имеется обратная статистическая связь. На это указывают отрицательные значения параметра b1 линейного, степенного и логарифмического уравнений регрессии, а также меньшее единицы значение параметра b1 показательного уравнения. Все уравнения регрессии статистически значимы на уровне значимости a=0,05 ( 

Угловой коэффициент b1=–0,933 линейной регрессии показывает, что при увеличении цены шампуня X на 1 руб. количество проданных упаковок Y уменьшается в среднем на 0,933 шт. Линейная модель объясняет 78,8 % вариации Y (R 2 =0,788). Предсказанные уравнением регрессии значения Y отличаются от фактических значений в среднем на 11,8 %.
Показатель степени b1=–0,888 степенной регрессии показывает, что при увеличении цены X на 1 % число реализованных упаковок Y уменьшается в среднем на 0,888 %. Степенная модель объясняет 85,7 % вариации Y. Предсказанные уравнением регрессии значения Y отличаются от фактических в среднем на 9,7 %.
Значение параметра b1=39,6 логарифмической регрессии показывает, что при увеличении цены единицы продукции X на 1 % количество проданных упаковок Y уменьшается в среднем на 
Значение основания степени b1=0,979 показательной регрессии показывает, что при увеличении цены X на 1 руб. объем реализации Y составит в среднем 97,9 % от первоначального значения, или, другими словами, уменьшится на 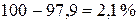
2. Сравнивая между собой коэффициенты детерминации R 2 четырех построенных моделей, приходим к выводу, что лучшей является степенная модель, имеющая наибольший R 2 . Эту модель и целесообразно использовать в качестве рабочей для анализа и прогнозирования изменения объема реализации Y от изменения цены единицы продукции X.
Контрольные задания
Используя приведенные ниже данные, выполнить расчеты в соответствии с заданием к примерам 2.1 и 2.2. В вариантах 1 – 5 между переменными присутствует прямая связь, в вариантах 6 – 10 — обратная связь.
Вариант 1(прямая связь)
| Наблюдение |
| Y |
| X |
Вариант 2(прямая связь)
| Наблюдение |
| Y |
| X |
Вариант 3(прямая связь)
| Наблюдение |
| Y |
| X |
Вариант 4(прямая связь)
| Наблюдение |
| Y |
| X |
Вариант 5(прямая связь)
| Наблюдение |
| Y |
| X |
Вариант 6(обратная связь)
| Наблюдение |
| Y |
| X |
Вариант 7(обратная связь)
| Наблюдение |
| Y |
| X |
Вариант 8(обратная связь)
| Наблюдение |
| Y |
| X |
Вариант 9(обратная связь)
| Наблюдение |
| Y |
| X |
Вариант 10(обратная связь)
| Наблюдение |
| Y |
| X |
Тестовые вопросы для самоконтроля
Из перечня предлагаемых ответов на вопрос только один является правильным. Правильные ответы приведены на с. 151. Числовые данные тестов можно использовать как исходные для рассмотренных в § 2.7 примеров.
По десяти интернет-брокерам в секции фондового рынка имеются данные, характеризующие зависимость годового торгового оборота (Y, млрд. руб.) от средней ставки маржинального кредитования (X, % годовых):
| Компания | А | Б | В | Г | Д | Е | Ж | З | И | К |
| Y | 30,82 | 30,8 | 25,14 | 14,1 | 12,73 | 10,8 | 9,74 | 8,42 | 7,65 | |
| X | 16,5 |
Парный коэффициент линейной корреляции между переменными Y и X имеет значение ry,x=–0,451.
Охарактеризовать линейную связь между торговым оборотом Y и средней ставкой маржинального кредитования X, если критическое значение коэффициента корреляции на уровне значимости a=0,05 составляет rкр=0,632.
а) Линейная связь статистически значимая.
б) Линейная связь статистически незначимая.
в) Линейная связь тесная.
г) Линейная связь прямая функциональная.
д) Линейная связь обратная функциональная.
По семи целлюлозно-бумажным компаниям имеются данные, характеризующие зависимость объема выпускаемой продукции (Y, млн. долл. США) от производственной мощности (X, тыс. тонн целлюлозы в год), по итогам года:
| Компания | А | Б | В | Г | Д | Е | Ж |
| Y | |||||||
| X |
Стандартные отклонения переменных Y и X и парный коэффициент корреляции между ними имеют соответственно значения: Sy=344 млн. долл. США, Sx=824 тыс. тонн, ry,x=0,988.
На сколько в среднем увеличивается объем выпускаемой продукции Y при росте производственной мощности X на одну тысячу тонн целлюлозы в год?
а) На 0,344 млн. долл.
б) На 0,824 млн. долл.
в) На 0,412 млн. долл.
г) На 0,988 млн. долл.
д) На 0,280 млн. долл.
Исследуется связь между официальными курсами доллара США (Y, руб./USD) и евро (X, руб./EUR), установленными Центральным банком Российской Федерации. Имеются данные за десять последовательных дней:
| День | ||||||||||
| Y | 28,11 | 27,97 | 27,97 | 28,01 | 27,98 | 28,12 | 28,19 | 28,13 | 28,09 | 28,07 |
| X | 36,59 | 36,46 | 36,56 | 36,47 | 36,28 | 36,13 | 35,98 | 35,97 | 36,00 | 36,13 |
Методом наименьших квадратов было получено уравнение линейной регрессии Y по X:

Суммы квадратов отклонений зависимой переменной Y от своего среднего значения составляют:
· обусловленная регрессией — SSрег=0,0240;
Рассчитать F-статистику и проверить статистическую значимость уравнения регрессии, если табличное значение F‑критерия Фишера на уровне значимости a=0,05 составляет Fтаб=5,32.
а) F=6,17; уравнение регрессии статистически значимо.
б) F=0,77; уравнение регрессии статистически незначимо.
в) F=1,77; уравнение регрессии статистически незначимо.
г) F=2,54; уравнение регрессии статистически незначимо.
д) F=14,17; уравнение регрессии статистически значимо.
По девяти из наиболее прибыльных компаний региона имеются данные, характеризующие зависимость чистой прибыли (Y, млн. руб.) от объема реализации (X, млн. руб.) по итогам одного года:
| Компания | А | Б | В | Г | Д | Е | Ж | З | И |
| Y | |||||||||
| X |
Методом наименьших квадратов было получено уравнение линейной регрессии Y по X:

Коэффициент детерминациисоставляет R 2 =0,540.
Рассчитать F-статистику и проверить статистическую значимость уравнения регрессии на уровне a=0,05, если табличное значение F‑критерия Фишера составляет Fтаб=5,59.
а) F=0,73; уравнение регрессии статистически незначимо.
б) F=1,17; уравнение регрессии статистически незначимо.
в) F=3,91; уравнение регрессии статистически значимо.
г) F=8,22; уравнение регрессии статистически значимо.
д) F=22,6; уравнение регрессии статистически значимо.
По восьми крупнейшим западным банкам-консультантам на рынке M&A (сопровождение сделок по слияниям и поглощениям) имеются данные, характеризующие зависимость размера комиссионных (Y, млн. долл. США) от объема сделок (X, млрд. долл. США), по итогам трех кварталов года:
| Банк | А | Б | В | Г | Д | Е | Ж | З |
| Y | ||||||||
| X | 305,5 | 265,7 | 240,4 | 149,3 | 101,6 | 114,6 | 122,2 |
Уравнение линейной регрессии Y по X имеет вид:

Стандартные ошибки коэффициентов уравнения составляют:
· свободного коэффициента — 
· углового коэффициента — 
Проверить статистическую значимость уравнения регрессии на уровне значимости a=0,05 для чего рассчитать соответствующую t-статистику. Табличное значение t‑критерия Стьюдента составляет tтаб=2,447.
а) t=0,892; уравнение регрессии статистически незначимо.
б) t=2,510; уравнение регрессии статистически значимо.
в) t=1,121; уравнение регрессии статистически незначимо.
г) t=3,404; уравнение регрессии статистически значимо.
д) t=3,816; уравнение регрессии статистически значимо.
По семи оценочным компаниям имеются данные, характеризующие зависимость совокупной выручки за полугодие (Y, тыс. руб.) от количества специалистов-оценщиков (X, чел.):
| Компания | А | Б | В | Г | Д | Е | Ж |
| Y | |||||||
| X |
С помощью «Мастера диаграмм» EXCEL были получены уравнения линейной, степенной, показательной и логарифмической регрессий Y по X, и для каждой модели определен коэффициент детерминации R 2 :
· линейная: 
· степенная: 
· показательная: 
· логарифмическая: 
Какая из моделей лучше характеризует вариацию совокупной выручки Y?
Исследуется связь между ценой нефти марки Urals (Y, долл. США/баррель) и ценой нефти марки Brent (X, долл./баррель) по итогам торгов на Международной нефтяной бирже за десять торговых дней:
| День | ||||||||||
| Y | 39,91 | 41,18 | 40,38 | 39,4 | 39,44 | 39,54 | 40,04 | 38,42 | 38,49 | 39,81 |
| X | 44,8 | 45,87 | 44,64 | 43,65 | 43,38 | 43,69 | 43,05 | 42,93 | 42,98 | 44,42 |
Было получено уравнение линейной регрессии Y по X:

Дать правильную экономическую интерпретацию угловому коэффициенту b1=0,715 уравнения регрессии.
Угловой коэффициент b1=0,715 уравнения регрессии показывает, что …
а) … 71,5 % вариации цены нефти Urals объясняется вариацией цены нефти Brent.
б) … с ростом цены нефти Brent на один процент цена нефти Urals возрастает в среднем на 0,715 %.
в) … с ростом цены нефти Brent на один процент цена нефти Urals возрастает в среднем на 0,715 долл./баррель.
г) … с ростом цены барреля нефти Brent на один доллар цена барреля нефти Urals возрастает в среднем на 0,715 %.
д) … с ростом цены барреля нефти Brent на один доллар цена барреля нефти Urals возрастает в среднем на 0,715 доллара.
Исследуется зависимость месячного торгового оборота универсального магазина (Y, млн. руб.) от размера торговых площадей (X, м 2 ). Имеются данные по восьми универмагам города:
| Магазин | А | Б | В | Г | Д | Е | Ж | З |
| Y | ||||||||
| X |
Было получено уравнение степенной регрессии Y по X:

Дать правильную экономическую интерпретацию показателю степени b1=0,552 в уравнении регрессии.
Показатель степени b1=0,552 в уравнении регрессии показывает, что …
а) … 55,2 % вариации торгового оборота объясняется вариацией размера торговых площадей.
б) … с увеличением размера торговых площадей на один процент торговый оборот возрастает в среднем на 0,552 %.
в) … с увеличением размера торговых площадей на один процент торговый оборот возрастает в среднем на 0,552 млн. руб.
г) … с увеличением размера торговых площадей на один квадратный метр торговый оборот возрастает в среднем на 0,552 %.
д) … с увеличением размера торговых площадей на один квадратный метр торговый оборот возрастает в среднем на 0,552 млн. руб.
По девяти туристическим агентствам города исследуется зависимость месячного торгового оборота (Y, тыс. долл. США) от количества менеджеров по туризму (X, чел.):
| Турагентство | А | Б | В | Г | Д | Е | Ж | З | И |
| Y | |||||||||
| X |
Было получено уравнение показательной регрессии Y по X:

Дать правильную экономическую интерпретацию основанию степени b1=1,076 в уравнении регрессии.
Основание степени b1=1,076 в уравнении регрессии показывает, что …
а) … с увеличением численности менеджеров по туризму на одного человека торговый оборот возрастает в среднем в 1,076 раз, т.е. на 7,6 %.
б) … с увеличением численности менеджеров по туризму на одного человека торговый оборот возрастает в среднем на 1,076 %.
в) … с увеличением численности менеджеров по туризму на одного человека торговый оборот возрастает в среднем на 1,076 тыс. руб.
г) … с увеличением численности менеджеров по туризму на один процент торговый оборот возрастает в среднем в 1,076 раз, т.е. на 7,6 %.
д) … 1,076 % вариации торгового оборота объясняется вариацией численности менеджеров по туризму.
Исследуется связь между учетной ценой Банка России на аффинированное золото (Y, руб./г) и ценой золота на мировых рынках (X, долл. за тройскую унцию) по данным за десять последовательных дней:
| День | ||||||||||
| Y | 390,38 | 391,74 | 393,61 | 378,8 | 377,01 | 381,28 | 383,09 | 372,84 | 374,48 | 381,19 |
| X | 438,9 | 441,1 | 422,2 | 422,5 | 423,3 | 426,8 | 415,9 | 418,85 | 427,1 |
Методом наименьших квадратов было получено уравнение линейной регрессии Y по X:

Построить интервальный прогноз учетной цены Банка России на аффинированное золото y0 с надежностью 90 % при цене золота x0=410 долл. за тройскую унцию, если стандартная ошибка прогноза фактического значения Y при этом составляет 
С вероятностью 0,9 учетная цена золота будет находиться в интервале …
Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Дать экономическую интерпретацию параметров уравнения
Все эти эффекты затрудняют и без того сложную задачу интерпретации коэффициентов регрессии или вообще делают невозможным ее решение без привлечения новых способов обработки и дополнительной информации. В этих условиях нельзя применять уравнение регрессии и для прогноза значений переменной у. В то же время если уравнение регрессии предполагается использовать для целей прогноза значений переменной у только в точках, близких к значениям объясняющих переменных х(1 . . х из матрицы данных X, то оно может оказаться вполне удовлетворительным независимо от степени связи между предсказывающими переменными качество уравнения регрессии определяется значением коэффициента множественной корреляции Ry.x между переменной у и переменными X (хотя при этом может быть необходимо принять некоторые предосторожности чисто вычислительного характера). Таким образом, последствия мультиколлинеарности тем серьезнее, чем больше информации мы хотим получить из имеющейся совокупности наблюдений. [c.254]
Более правильной на первый взгляд кажется интерпретация коэффициента регрессии а как обусловленная фактором Xi часть интенсивности совместного влияния всех факторов. Коэффициент регрессии а, показывает, на сколько единиц изменяется результативный показатель У в случае изменения факторного показателя Xi на единицу при изменении других факторных показателей аналогично их изменению в условиях исследуемого эксперимента (в рамках исследуемой статистической совокупности наблюдений). Данная интерпретация как будто вообще устраняет проблему применяемости модели — каждая модель по данному формальному подходу имеет содержательную интерпретацию и, следовательно, ее можно применять в процессе принятия решений в качестве истинного отображения реальных связей. Подобное мнение опровергается практикой статистического моделирования. Формальная интерпретация интенсивности влияния отдельных факторов часто противоречит здравому смыслу и практическому опыту субъекта управления. Это означает, что интерпретация коэффициентов регрессии не отражает их сущности. [c.122]
Интерпретация моделей регрессии осуществляется методами той отрасли знаний, к которой относятся исследуемые явления. Но всякая интерпретация начинается со статистической оценки уравнения регрессии в целом и оценки значимости входящих в модель факторных признаков, т.е. с выяснения, как они влияют на величину результативного признака. Чем больше величина коэффициента регрессии, тем значительнее влияние данного признака на моделируемый. Особое значение при этом имеет знак перед коэффициентом регрессии, который говорит о характере влияния на результативный признак. Если факторный признак имеет знак плюс, то с увеличением данного фактора результативный признак возрастает если факторный признак имеет знак минус, то с его увеличением результативный признак уменьшается. [c.121]
Линейный коэффициент корреляции изменяется в пределах от -1 до +1. Знаки коэффициентов регрессии и корреляции совпадают. При этом интерпретацию значений коэффициента корреляции можно представить следующим образом. [c.123]
Следует отметить, что в принципе качественное различие можно формализовать с помощью любой переменной, принимающей два разных значения, не обязательно О или 1 . Однако в эконометрической практике почти всегда используются фиктивные переменные типа 0—1 , так как при этом интерпретация полученных результатов выглядит наиболее просто. Так, если бы в модели (5.2) в качестве фиктивной выбрали переменную Zj, принимающую значения z,i=4 (для работников-мужчин) и 2/2=1 (для женщин), то коэффициент регрессии оц при этой переменной равнялся бы 1/(4— 1), т. е. одной трети среднего изменения заработной платы у мужчин. [c.117]
Если рассматриваемый качественный признак имеет несколько (k) уровней (градаций), то в принципе можно было ввести в регрессионную модель дискретную переменную, принимающую такое же количество значений (например, при исследовании зависимости заработной платы Y от уровня образования Z можно рассматривать Л=3 значения z,-i=l при наличии начального образования, гд=2 — среднего и г,з=3 при наличии высшего образования). Однако обычно так не поступают из-за трудности содержательной интерпретации соответствующих коэффициентов регрессии, а вводят (k—l) бинарных переменных. [c.117]
Дайте интерпретацию коэффициента эластичности данной модели регрессии. [c.36]
Выберите наилучшее уравнение регрессии. Дайте интерпретацию их параметров и доверительных интервалов для коэффициентов регрессии. [c.84]
Выберите наилучшее уравнение регрессии. Дайте интерпретацию его параметров и доверительных интервалов для коэффициентов регрессии на примере одного из факторных признаков. [c.85]
Поскольку коэффициент регрессии в эконометрических исследованиях имеет четкую экономическую интерпретацию, то доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, —10 0, то эффективность данной ценной бумаги повышаться при росте эффективности рынка. При Р хь, хв. Между собой они причинно не связаны. В соответствии с нормами технических условий из общей массы выделялись годные приборы и анализировалась как вся масса приборов, так и годные. Это позволило попытаться уловить различие во взаимосвязи параметров приборов до и после их отбраковки. Эмпирические корреляционные отношения рассчитывались только для годных приборов, поскольку разброс параметров для всей совокупности приборов был настолько велик, что подсчитывать корреляционные отношения не имело смысла. Доверительные интервалы ввиду большого объема выборки подсчитывались по формуле [37]. Сравнение парных коэффициентов корреляции с эмпирическими отношениями использовалось для проверки линейности связи между параметрами. Эмпирическому корреляционному отношению приписывается тот знак, который имеет парный коэффициент корреляции. Связь считается линейной, если корреляционное отношение попадает в доверительный интервал для парного коэффициента корреляции. Может показаться, что мы противоречим высказанному выше утверждению о том, что не существует формальных методов, позволяющих определить форму связи. Однако в данном случае мы говорим не об определении формы связи с целью, например, нахождения параметров уравнения регрессии и дальнейшей интерпретации или экстраполяции в каком-либо виде. Единственная наша забота состоит в том, чтобы парные коэффициенты корреляции (или иные оценки тесноты связи) были действительными характеристиками связи. В табл. 94 приведены в первой строке каждой клетки — парный коэф- [c.188]
Построенное уравнение регрессии в любом случае требует определенной интерпретации и анализа. Интерпретация требует словесного описания полученных результатов с трактовкой найденных коэффициентов, с тем чтобы построенная зависимость стала понятной человеку, не являющемуся специалистом в эконометрическом анализе. В нашем примере коэффициент b>i может трактоваться как предельная [c.106]
Интерпретация коэффициента регрессии как углового коэффициента в линейном уравнении для нелинейной зависимости не годится. Определить изменение У при изменении X на единицу можно с помощью производной (простой или частной), взятой по соответствующему фактору X. Так, для степенного уравнения У = а0Ха производная по X равна [c.136]
При интерпретации коэффициентов регрессии следует иметь в виду, что чем меньше индекс браузинга (зависимая переменная), тем сильнее покупатели склонны демонстрировать поведение, с магазина без определенной Два предиктора с [c.669]
Кроме того, при интерпретации коэффициентов множественной рефессии предполагается независимость факторов друг от друга, что становится невозможным при рассмотрении системы совместных уравнений. Так, в нашем примере уравнение регрессии у = —1,09 + 0,364у2 + 1,192л , показывает, что с ростом х на единицу у возрастает в среднем на 1,192 ед. при неизменном уровне значения у2. Между тем в соответствии с системой одновременных уравнений переменная у2 не может быть неизменной, ибо она в свою очередь зависит от yt. [c.199]
Значения -коэффициента заключены в интервале [—
🔥 Видео
Эконометрика. Линейная парная регрессияСкачать

Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать

Эконометрика Линейная регрессия и корреляцияСкачать

Mavzu: Задачи парной линейной регрессиСкачать

Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Эконометрика. Множественная регрессия и корреляция.Скачать

Коэффициент детерминации. Основы эконометрикиСкачать

Как спрос и предложение задают ценыСкачать

Расчет коэффициента корреляции в ExcelСкачать

Парная регрессия: линейная зависимостьСкачать

Множественная регрессияСкачать

Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать

Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать

Эконометрика 1 ВведениеСкачать

Множественная регрессия в ExcelСкачать