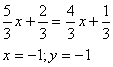Даны уравнения высот треугольника abc 2x 3y 1 0 (7 видео)

Даны уравнения высот треугольника abc 2x 3y 1 0

Даны уравнения высот треугольника 2x — 3y + 1 = 0 и x + y = 0 и координаты одной из его вершин A(1, 2). Найти уравнения сторон треугольника.

Точка A(1, 2) не принадлежит данным в условии высотам треугольника, так как ее координаты не удовлетворяют их уравнениям: и . Отсюда следует, что высоты, данные в задаче, проведены из двух других вершин треугольника B и C (см. рисунок)

Назовем их CD и BE, CD AB, BE AC. Пусть высота CD имеет уравнение x + y = 0, а уравнение высоты BE 2x — 3y + 1 = 0. Так как AC BE, то уравнение AC мы найдем из уравнения семейства прямых, перпендикулярных BE, приняв во внимание, что искомая прямая проходит через данную точку A(1, 2).

Сторона AC имеет уравнение 3x + 2y — 7 = 0. Уравнение прямой AB найдем, как уравнение прямой, проходящей через точку A(1, 2) перпендикулярно CD. Оно имеет вид

Теперь следует найти координаты точек B и C:

Уравнение стороны BC 2x + 3y + 7 = 0.

Таким образом, уравнения всех трех сторон треугольника найдены.

Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Даны уравнения высот треугольника abc 2x 3y 1 0

Угловой коэффициент уравнения стороны ВС можно найти из уравнения высоты АМ (эта высота перпендикулярна ВС по заданию)

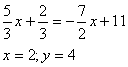
Остается найти свободный член. Для этого подставим значение точки В. Теперь, запишем:

Для нахождения координат точки А приравняем левые части уравнений АВ и АМ:

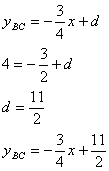
Угловой коэффициент уравнения стороны АС можно найти из уравнения высоты BN (эта высота перпендикулярна АС по заданию)

Остается найти свободный член. Для этого подставим значение точки А. Теперь, запишем:

Для нахождения координат точки С приравняем левые части уравнений ВС и АС:

Угловой коэффициент уравнения высоты КС можно найти из уравнения стороны АB (эта высота перпендикулярна АВ по заданию)

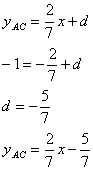
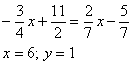
Остается найти свободный член. Для этого подставим значение точки С. Теперь, запишем:

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Даны уравнения 2х высот треугольника АВС: х+у-2=0 9х-3у-4=0, координаты вершины А (2;2), составить уравнение сторон

1. Т. к. координаты точки А не удовлетворяют ни одному из данных уравнений высот, то эти высоты проходят через точки В и С и перпендикулярны сторонам АВ и АС
2. Чтобы найти уравнения сторон АВ и АС нам достаточно найти хоть один вектор, перпендикулярный данным сторонам. Т. к. высоты перпендикулярны сторонам АВ и АС, то любой вектор, принадлежащий данной высоте перпендикулярен соответствующей стороне
3. Найдем векторы, принадлежащие прямым:
х+у-2=0 и 9х-3у-4=0
Выразим:
x = 2 — y;
y = 3x — 4/3
Чтобы найти первую точку положим х = 0:
у = 2
у = -4/3
Итак мы нашли по одной точке на каждой из высот:
(0, 2) и (0, -4/3)
Найдем еще две точки. Для этого положим у = 0:
х = 2
х = 4/9
Итак мы нашли еще две точки на данных прямых:
(2, 0) и (4/9, 0)
Найдем координаты векторов, принадлежащих данным прямым (высотам) :
N1(2,-2) и N2(4/9, 4/3)
4. Теперь у нас есть все, чтобы найти уравнения прямых АВ и АС: т. е. векторы N1 и N2, перпендикулярные этим прямым и точка А, лежащая на данных прямых.
Строим общее уравнение прямых:
АВ: 2х — 2у + K = 0
AC: 4x/9 + 4y/3 + M = 0
Чтобы найти коэффициенты К и М подставим в уравнения координаты точки А:
4 — 4 + K = 0
K = 0
8/9 + 8/3 + M = 0
M = — 32/9
Окончательно получаем уравнения прямых АВ и АС:
AB: 2x — 2y = 0
AC: 4x/9 + 4y/3 — 32/9 = 0
Упростим уравнение стороны АС умножив его на 9:
4x + 12y — 32 = 0
5. Найдем точки В и С. Точка В находится на пересечении прямых 2x + 2y — 8 = 0 и х+у-2=0.
Решая совместно систему:
2x — 2y = 0
х+у-2=0.
Получим: х = 1, у = 1
Т. е. точка В имеет координаты (1, 1)
Аналогично из системы:
4x + 12y — 32 = 0
9х — 3у — 4 = 0
Найдем координаты точки С (1.2, 2.66)
6. Найдем каноническое уравнение прямой ВС. Для этого найдем координаты вектора ВС:
ВС (0.2, 1,66)
Используя координаты точки В и координаты вектора ВС построим уравнение стороны ВС:
(x — 1)/0.2 = (y — 1)/1.66
Вот и все. Уравнения всех трех сторон найдены.
Успехов!