Даны уравнения двух сторон прямоугольника 2x 3y 5 0 3x 2y 7

Условие

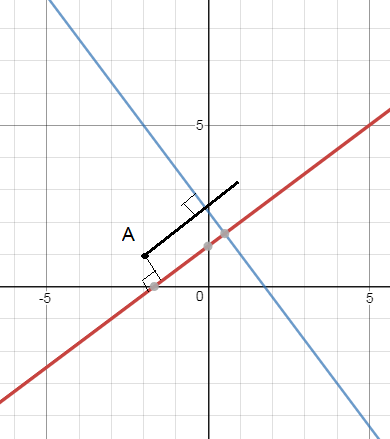
Помогите, пожалуйста, с задачей. Даны уравнения сторон прямоугольника 3х-4у+5=0, 4х+3у-7=0 и одна из его вершин А(-2;1). Составить уравнения двух других сторон прямоугольника.

Решение

Очевидно, что точка А не принадлежит ни одной из данных сторон, подставляем ее координаты в уравнение и убеждаемся, что координаты не удовлетворяют ни первому , ни второму уравнению
3*(-2)-4*1+5=0- неверно
4*(-2)+3*1-7=0 -неверно

Так как прямые
3х–4у+5=0 и 4х+3у–7=0
пересекаются под прямым углом, то дальнейшее решение видно из рисунка.
На рисунке проводим через точку А две прямые, перпендикулярные данным ( или параллельные данным как хотите)
Можно и так и так.

Находим уравнение прямой перпендикулярной
3х–4у+5=0
y=(3/4)x+(5/4)
k=3/4

Значит k=-4/3 — угловой коэффициент перпендикулярной прямой

y=(-4/3)x+b
Чтобы найти b подставляем координаты точки А
1=(-4/3)*2+b
b=11/3
y=(-4/3)x+(11/3)
[b]4x+3y-11=0[/b]

Находим уравнение прямой перпендикулярной
4х+3у–7=0
y=(-4/3)x+(7/3)
k=-4/3

Значит k=3/4 — угловой коэффициент перпендикулярной прямой

y=(3/4)x+b
Чтобы найти b подставляем координаты точки А
1=(3/4)*2+b
b=-1/2
y=(3/4)x+(-1/2)
[b]3x-4y-1=0[/b]

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Калькулятор онлайн.
Решение системы двух линейных уравнений с двумя переменными.
Метод подстановки и сложения.

С помощью данной математической программы вы можете решить систему двух линейных уравнений с двумя переменными методом подстановки и методом сложения.

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения двумя способами: методом подстановки и методом сложения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.

При вводе уравнений можно использовать скобки. При этом уравнения сначала упрощаются. Уравнения после упрощений должны быть линейными, т.е. вида ax+by+c=0 с точностью порядка следования элементов.
Например: 6x+1 = 5(x+y)+2

В уравнениях можно использовать не только целые, но также и дробные числа в виде десятичных и обыкновенных дробей.

Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например: 2.1n + 3,5m = 55

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &

Примеры.
-1&2/3y + 5/3x = 55
2.1p + 55 = -2/7(3,5p — 2&1/8q)

Решить систему уравнений

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Немного теории.

Видео:найти уравнения биссектрис углов между прямымиСкачать

Решение систем линейных уравнений. Способ подстановки

Последовательность действий при решении системы линейных уравнений способом подстановки:
1) выражают из какого-нибудь уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ left< begin 3x+y=7 \ -5x+2y=3 end right. $$

Выразим из первого уравнения y через x: y = 7-3x. Подставив во второе уравнение вместо y выражение 7-Зx, получим систему:
$$ left< begin y = 7—3x \ -5x+2(7-3x)=3 end right. $$

Нетрудно показать, что первая и вторая системы имеют одни и те же решения. Во второй системе второе уравнение содержит только одну переменную. Решим это уравнение:
$$ -5x+2(7-3x)=3 Rightarrow -5x+14-6x=3 Rightarrow -11x=-11 Rightarrow x=1 $$

Подставив в равенство y=7-3x вместо x число 1, найдем соответствующее значение y:
$$ y=7-3 cdot 1 Rightarrow y=4 $$

Пара (1;4) — решение системы

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений, также считают равносильными.

Видео:14. Угол между прямыми в пространствеСкачать

Решение систем линейных уравнений способом сложения

Рассмотрим еще один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Последовательность действий при решении системы линейных уравнений способом сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ left< begin 2x+3y=-5 \ x-3y=38 end right. $$

В уравнениях этой системы коэффициенты при y являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной 3x=33. Заменим одно из уравнений системы, например первое, уравнением 3x=33. Получим систему
$$ left< begin 3x=33 \ x-3y=38 end right. $$

Из уравнения 3x=33 находим, что x=11. Подставив это значение x в уравнение ( x-3y=38 ) получим уравнение с переменной y: ( 11-3y=38 ). Решим это уравнение:
( -3y=27 Rightarrow y=-9 )

Таким образом мы нашли решение системмы уравнений способом сложения: ( x=11; y=-9 ) или ( (11; -9) )

Воспользовавшись тем, что в уравнениях системы коэффициенты при y являются противоположными числами, мы свели ее решение к решению равносильной системы (сумировав обе части каждого из уравнений исходной симтемы), в которой одно из уравнений содержит только одну переменную.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Калькулятор Уравнений. Решение Уравнений Онлайн

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

🎥 Видео

Математика без Ху!ни. Уравнение плоскости.Скачать

Как решать кубические уравнения Решите уравнение 3 степени 9 класс Разложить на множители ДелениеСкачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

№5 Линейное уравнение 2-3(2х+2)=5-4х Простое уравнение со скобками 6кл 7кл 8кл 9кл 11кл ОГЭ ЕГЭСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Решите уравнение ★ x^6-2x^5-x^4+3x^3+x^2-2x-1=0Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Составляем уравнение прямой по точкамСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Задача про соотношение сторон. Геометрия 7 класс.Скачать

№2 Линейное уравнение 2+3х=-2х-13 Как решать простое уравнение Решите уравнение 5кл 6кл 7кл ОГЭ ЕГЭСкачать

Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать