С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
- Предупреждение
- Точка пересечения прямых в пространстве − теория, примеры и решения
- 1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
- 2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
- 3. Точка пересечения прямых в пространстве, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
- Даны две прямые установить пересекаются они скрещиваются или параллельны
- Взаимное расположение двух прямых в пространстве. Признак скрещивающихся прямых. Угол между скрещивающимися прямыми
- Взаимное расположение двух прямых в пространстве
- Признак скрещивающихся прямых
- Угол между скрещивающимися прямыми
- 5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых
- Задачи с решениями
- Взаимное расположение двух прямых в пространстве. Признак скрещивающихся прямых. Угол между скрещивающимися прямыми
- Взаимное расположение двух прямых в пространстве
- Признак скрещивающихся прямых
- Угол между скрещивающимися прямыми
- 💥 Видео
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Точка пересечения прямых в пространстве − теория, примеры и решения
- Содержание
- 1. Точка пересечения прямых, заданных в каноническом виде.
- 2. Точка пересечения прямых, заданных в параметрическом виде.
- 3. Точка пересечения прямых, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
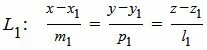 , , | (1) |
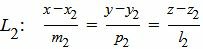 , , | (2) |
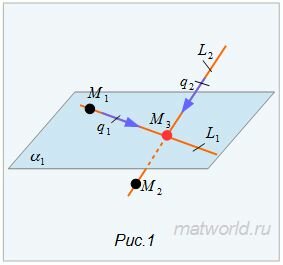
Найти точку пересечения прямых L1 и L2 (Рис.1).
 |
Запишем уравнение (1) в виде системы двух линейных уравнений:
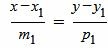 , , | (3) |
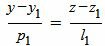 | (4) |
Сделаем перекрестное умножение в уравнениях (3) и (4):
| p1(x−x1)=m1(y−y1) |
| l1(y−y1)=p1(z−z1) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p1x−m1y=p1x1−m1y1, | (5) |
| l1y−p1z=l1y1−p1z1. | (6) |
Аналогичным образом преобразуем уравнение (2):
Запишем уравнение (2) в виде системы двух линейных уравнений:
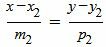 , , | (7) |
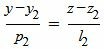 | (8) |
Сделаем перекрестное умножение в уравнениях (7) и (8):
| p2(x−x2)=m2(y−y2) |
| l2(y−y2)=p2(z−z2) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p2x−m2y=p2x2−m2y2, | (9) |
| l2y−p2z=l2y2−p2z2. | (10) |
Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:
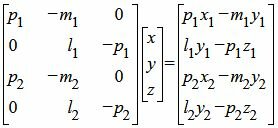 | (11) |
Как решить систему линейных уравнений (11)(или (5), (6), (9), (10)) посмотрите на странице Метод Гаусса онлайн. Если система линейных уравнениий (11) несовместна, то прямые L1 и L2 не пересекаются. Если система (11) имеет множество решений, то прямые L1 и L2 совпадают. Единственное решение системы линейных уравнений (11) указывает на то, что это решение определяет координаты точки пересечения прямых L1 и L2 .
2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
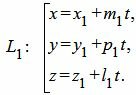 | (12) |
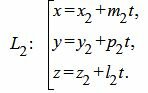 | (13) |
Задачу нахождения нахождения точки пересечения прямых L1 и L2 можно решить разными методами.
Метод 1. Приведем уравнения прямых L1 и L2 к каноническому виду.
Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:
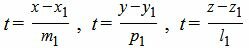 | (14) |
Так как левые части уравнений (14) равны, то можем записать:
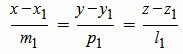 | (15) |
Аналогичным образом приведем уравнение прямой L2 к каноническому виду:
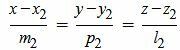 | (16) |
Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямых L1 и L2 решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:
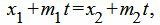 | (17) |
 | (18) |
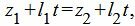 | (19) |
Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).
3. Точка пересечения прямых в пространстве, заданных в разных видах.
Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.
4. Примеры нахождения точки пересечения прямых в пространстве.
Пример 1. Найти точку пересечения прямых L1 и L2:
 | (20) |
 | (21) |
Представим уравнение (20) в виде двух уравнений:
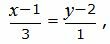 | (22) |
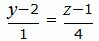 | (23) |
Сделаем перекрестное умножение в уравнениях (22) и (23):
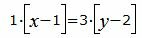 |
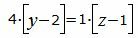 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
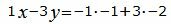 |
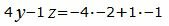 |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
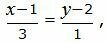 | (26) |
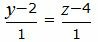 | (27) |
Сделаем перекрестное умножение в уравнениях (7) и (8)
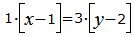 |
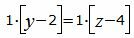 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
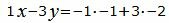 |
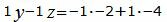 |
Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
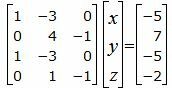 | (30) |
Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
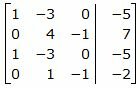 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1:
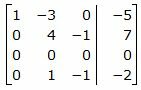 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:
 |
Сделаем перестановку строк 3 и 4.
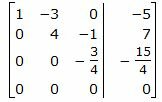 |
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:
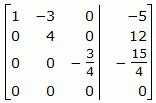 |
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:
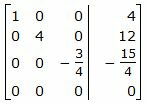 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
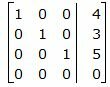 |
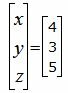 |
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Пример 2. Найти точку пересечения прямых L1 и L2:
 | (31) |
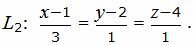 | (32) |
Приведем параметрическое уравнение прямой L1 к каноническому виду. Выразим параметр t через остальные переменные:
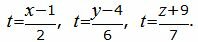 |
Из равентсв выше получим каноническое уравнение прямой:
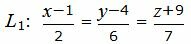 | (33) |
Представим уравнение (33) в виде двух уравнений:
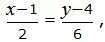 | (34) |
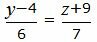 | (35) |
Сделаем перекрестное умножение в уравнениях (34 и (35):
 |
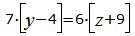 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
 |
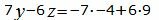 |
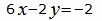 | (36) |
 . . | (37) |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
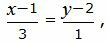 | (38) |
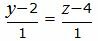 | (39) |
Сделаем перекрестное умножение в уравнениях (38) и (39)
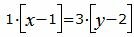 |
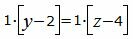 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
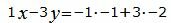 |
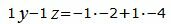 |
Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
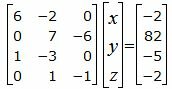 | (42) |
Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:
 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:
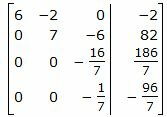 |
Исключим элементы 3-го столбца матрицы ниже элементаa33. Для этого сложим строку 4 со строкой 3, умноженной на -1/16:
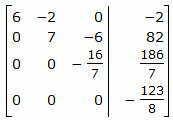 |
Из расширенной матрицы восстановим последнюю систему линейных уравнений:
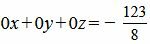 | (43) |
Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L1 и L2 не пересекаются. То есть они или параллельны, или скрещиваются.
Прямая L1 имеет направляющий вектор q1=, а прямая L2 имеет направляющий вектор q2=. Эти векторы не коллинеарны. Следовательно прямые L1 и L2 скрещиваются .
Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Даны две прямые установить пересекаются они скрещиваются или параллельны
Установить, пересекаются, параллельны или совпадают данные пары прямых; в случае пересечения прямых найти координаты точки их пересечения:
а) Найдем угловые коэффициенты прямых. Первое уравнение имеет вид 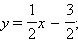
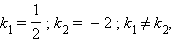
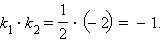
Отсюда получим
б) Умножим первое уравнение на (-2) и получим Это уравнение совпадает с уравнением второй прямой, т. е. прямые совпадают.
в) Умножим первое уравнение на (-3) и получим Второе уравнение имеет вид Коэффициенты при одинаковых переменных равно, но свободные члены при этом различны. Следовательно (см теорему 11.14) прямые параллельны.
Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Взаимное расположение двух прямых в пространстве.
Признак скрещивающихся прямых.
Угол между скрещивающимися прямыми
 Взаимное расположение двух прямых в пространстве Взаимное расположение двух прямых в пространстве |
 Признак скрещивающихся прямых Признак скрещивающихся прямых |
 Угол между скрещивающимися прямыми Угол между скрещивающимися прямыми |
Видео:10 класс - Геометрия - Скрещивающиеся прямыеСкачать

Взаимное расположение двух прямых в пространстве
Все возможные случаи взаимного расположения двух прямых в пространстве представлены в следующей таблице.
| Фигура | Рисунок | Определение |
| Две пересекающиеся прямые |  | Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку. |
| Две параллельные прямые | 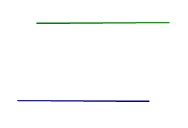 | Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек |
| Две скрещивающиеся прямые | 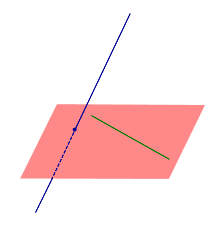 | Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые. |
| Две пересекающиеся прямые |
 |
Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.

Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек

Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.
С перечисленными в предыдущей таблице случаями взаимного расположения двух прямых в пространстве близко связаны утверждения, представленные в следующей таблице.
| Фигура | Рисунок | Тип утверждения и формулировка |
| Две различные точки | 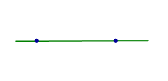 | Аксиома о прямой линии, заданной двумя точками Через две различные точки проходит одна и только одна прямая линия. |
| Прямая линия и точка, не лежащая на этой прямой | 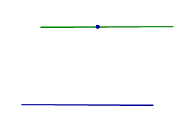 | Аксиома о параллельных прямых Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой. |
| Две пересекающиеся прямые | 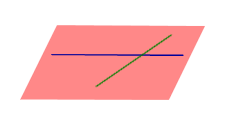 | Теорема о плоскости, определяемой двумя пересекающимися прямыми Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые. |
| Две параллельные прямые | 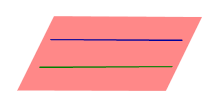 | Теорема о плоскости, определяемой двумя параллельными прямыми Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые. |
| Две различные точки |
 |
Аксиома о прямой линии, заданной двумя точками
Через две различные точки проходит одна и только одна прямая линия.

Аксиома о параллельных прямых
Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.

Теорема о плоскости, определяемой двумя пересекающимися прямыми
Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Теорема о плоскости, определяемой двумя параллельными прямыми
Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.
Видео:7. Скрещивающиеся прямыеСкачать

Признак скрещивающихся прямых
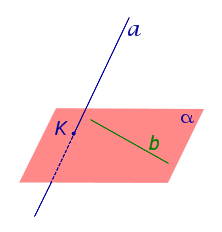
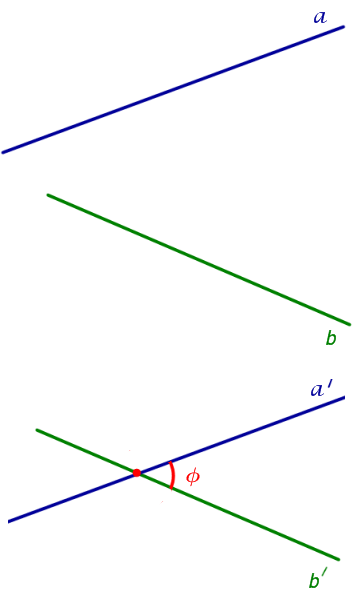
Признак скрещивающихся прямых . Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).
Доказательство . Напомним, что две прямые называют скрещивающимися, если не существует плоскости, содержащей обе эти прямые, и будем доказывать признак скрещивающихся прямых методом «От противного».
Для этого предположим, что прямая a , пересекающая плоскость в точке K , и прямая b , лежащая в плоскости α (рис. 1), не являются скрещивающимися. Из этого предположения следует, что существует плоскость, содержащая обе эти прямые. Обозначим эту плоскость буквой β и докажем, что плоскость β совпадает с плоскостью α . Действительно, поскольку обе плоскости α и β проходят через прямую b и точку K , не лежащую на этой прямой, то они совпадают. Следовательно, прямая a лежит в плоскости прямая a лежит в плоскости . Мы получили противоречие с тем, что по условию прямая a пересекает плоскость прямая a пересекает плоскость , а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.
Видео:15. Взаимное расположение прямых в пространствеСкачать

Угол между скрещивающимися прямыми
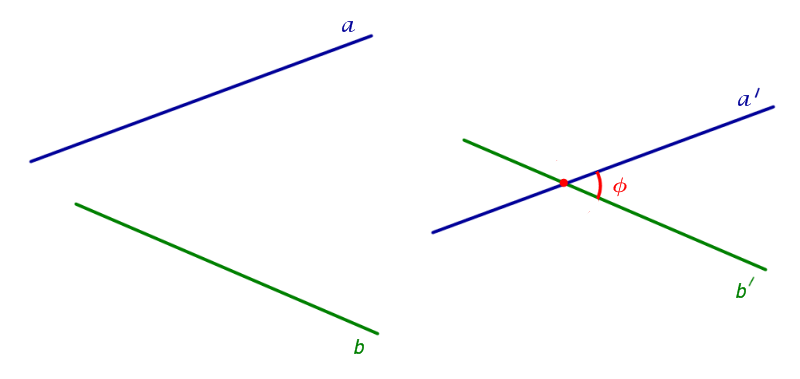
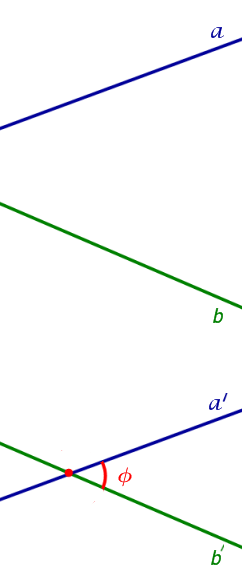
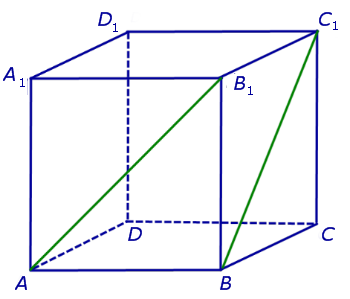
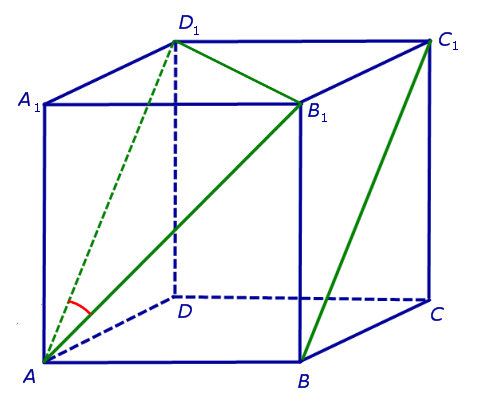
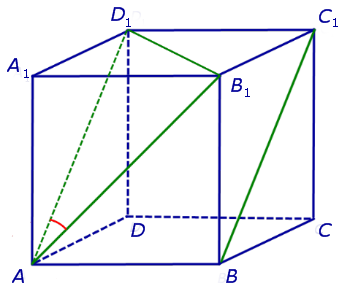
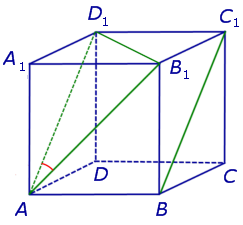
На рисунке 2 изображены скрещивающиеся прямые a и b . Прямая a’ параллельна прямой a , прямая b’ параллельна прямой b. Прямые a’ и b’ пересекаются. Угол φ и является углом между скрещивающимися прямыми a и b .
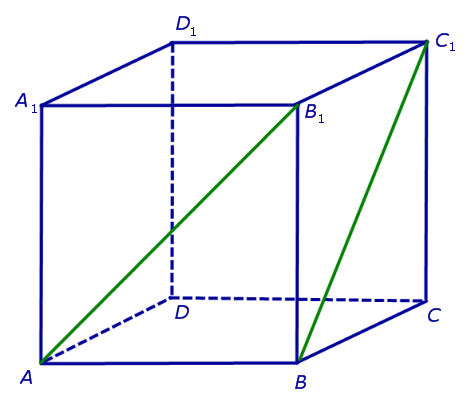
Для того, чтобы найти угол между прямыми AB1 и BC1 , проведем в кубе диагональ боковой грани AD1 и диагональ верхнего основания D1B1 (рис. 4).
Замечание . Для более глубокого усвоения понятия «Скрещивающиеся прямые» рекомендуем ознакомиться с разделами нашего сайта «Свойства скрещивающихся прямых» и «Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости».
Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых
Видеоурок: Параллельные прямые, перпендикулярные к плоскости
Лекция: Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых

Если на плоскости имеются несколько прямых, то они либо рано или поздно пересекутся произвольно, либо под прямым углом, или же будут параллельными. Давайте же разберемся с каждым случаем.
Пересекающимися можно назвать те прямые, у которых будет хотя бы одна точка пересечения.
Вы спросите, почему хотя бы одна, не может же прямая пересечь другую прямую две или три раза. Вы правы! Но прямые могут полностью совпасть друг с другом. В таком случае общих точек будет бесконечное множество.

Параллельными можно назвать те прямые, которые никогда не пересекутся, даже на бесконечности.

Примеры параллельных прямых в жизни: два противоположных края экрана монитора, линии в тетрадях, а также многие другие части вещей, имеющих квадратную, прямоугольную и другие формы.
Когда хотят показать на письме, что одна прямая параллельная второй, то используют следующее обозначение a||b. Данная запись говорит, что прямая а параллельна прямой b.
При изучении данной темы важно понять еще одно утверждение: через некоторую точку на плоскости, которая не принадлежит данной прямой, можно провести единственную параллельную прямую. Но обратите внимание, снова поправка – на плоскости. Если рассматривать трехмерное пространство, то можно провести бесконечное множество прямых, которые не будут пересекаться, но будут скрещивающимися.
Утверждение, которое было описано выше, называется аксиомой о параллельности прямых.

Прямые можно назвать только в том случае перпендикулярными, если они пересекаются под углом, равным 90 градусов.
В пространстве через некоторую точку на прямой можно провести бесконечное множество перпендикулярных прямых. Однако, если речь идет о плоскости, то через одну точку на прямой можно провести единственную перпендикулярную прямую.

У любых скрещивающихся прямых есть вертикальные углы и смежные.
Если у углов, которые образованы двумя скрещивающимися прямыми, одна сторона общая, то они называются смежными:
Смежные углы в сумме дают 180 градусов.
Если же углы, образованные двумя скрещивающимися прямыми, не имеют общей стороны, то они называются вертикальными:
Вертикальные углы всегда равны.
Если же некоторая прямая пересекает две других прямых, то она называется секущей.
Частным случаем является секущая двух параллельных прямых:
 Задачи с решениями
Задачи с решениями 

Установить, пересекаются, параллельны или совпадают данные пары прямых; в случае пересечения прямых найти координаты точки их пересечения:
а) Найдем угловые коэффициенты прямых. Первое уравнение имеет вид 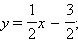
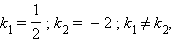
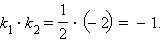
Отсюда получим
б) Умножим первое уравнение на (-2) и получим Это уравнение совпадает с уравнением второй прямой, т. е. прямые совпадают.
в) Умножим первое уравнение на (-3) и получим Второе уравнение имеет вид Коэффициенты при одинаковых переменных равно, но свободные члены при этом различны. Следовательно (см теорему 11.14) прямые параллельны.
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Взаимное расположение двух прямых в пространстве.
Признак скрещивающихся прямых.
Угол между скрещивающимися прямыми
 Взаимное расположение двух прямых в пространстве Взаимное расположение двух прямых в пространстве |
 Признак скрещивающихся прямых Признак скрещивающихся прямых |
 Угол между скрещивающимися прямыми Угол между скрещивающимися прямыми |
Видео:Следы прямой Взаимное положение двух прямыхСкачать

Взаимное расположение двух прямых в пространстве
Все возможные случаи взаимного расположения двух прямых в пространстве представлены в следующей таблице.
| Фигура | Рисунок | Определение |
| Две пересекающиеся прямые |  | Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку. |
| Две параллельные прямые |  | Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек |
| Две скрещивающиеся прямые |  | Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые. |
| Две пересекающиеся прямые |
 |
Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.

Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек

Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.
С перечисленными в предыдущей таблице случаями взаимного расположения двух прямых в пространстве близко связаны утверждения, представленные в следующей таблице.
| Фигура | Рисунок | Тип утверждения и формулировка |
| Две различные точки |  | Аксиома о прямой линии, заданной двумя точками Через две различные точки проходит одна и только одна прямая линия. |
| Прямая линия и точка, не лежащая на этой прямой |  | Аксиома о параллельных прямых Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой. |
| Две пересекающиеся прямые |  | Теорема о плоскости, определяемой двумя пересекающимися прямыми Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые. |
| Две параллельные прямые |  | Теорема о плоскости, определяемой двумя параллельными прямыми Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые. |
| Две различные точки |
 |
Аксиома о прямой линии, заданной двумя точками
Через две различные точки проходит одна и только одна прямая линия.

Аксиома о параллельных прямых
Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.

Теорема о плоскости, определяемой двумя пересекающимися прямыми
Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Теорема о плоскости, определяемой двумя параллельными прямыми
Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Признак скрещивающихся прямых
Признак скрещивающихся прямых . Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).
Доказательство . Напомним, что две прямые называют скрещивающимися, если не существует плоскости, содержащей обе эти прямые, и будем доказывать признак скрещивающихся прямых методом «От противного».
Для этого предположим, что прямая a , пересекающая плоскость в точке K , и прямая b , лежащая в плоскости α (рис. 1), не являются скрещивающимися. Из этого предположения следует, что существует плоскость, содержащая обе эти прямые. Обозначим эту плоскость буквой β и докажем, что плоскость β совпадает с плоскостью α . Действительно, поскольку обе плоскости α и β проходят через прямую b и точку K , не лежащую на этой прямой, то они совпадают. Следовательно, прямая a лежит в плоскости прямая a лежит в плоскости . Мы получили противоречие с тем, что по условию прямая a пересекает плоскость прямая a пересекает плоскость , а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.
Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Угол между скрещивающимися прямыми
На рисунке 2 изображены скрещивающиеся прямые a и b . Прямая a’ параллельна прямой a , прямая b’ параллельна прямой b. Прямые a’ и b’ пересекаются. Угол φ и является углом между скрещивающимися прямыми a и b .
Для того, чтобы найти угол между прямыми AB1 и BC1 , проведем в кубе диагональ боковой грани AD1 и диагональ верхнего основания D1B1 (рис. 4).
Замечание . Для более глубокого усвоения понятия «Скрещивающиеся прямые» рекомендуем ознакомиться с разделами нашего сайта «Свойства скрещивающихся прямых» и «Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости».
💥 Видео
Взаимное расположение прямых на плоскости. 7 класс.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Лекция №4 Чертеж прямой. Следы прямой. Прямые общего и частного положения. Взаимное положение прямыхСкачать

Параллельность прямых. Практическая часть. 10 класс.Скачать

Геометрия 10 класс (Урок№5 - Взаимное расположение прямых в пространстве.)Скачать

17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

✓ Расстояние между скрещивающимися прямыми | ЕГЭ-2018. Задание 13. Математика | Борис ТрушинСкачать

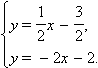
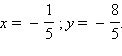





 Задачи с решениями
Задачи с решениями 
