Стороны треугольника заданы уравнениями:
Найти координаты вершин треугольника.
Координаты вершины A найдем, решая систему, составленную из уравнений сторон AB и AC:
Систему двух линейных уравнений с двумя неизвестными решаем способами, известными из элементарной алгебры, и получаем
Вершина A имеет координаты
Координаты вершины B найдем, решая систему из уравнений сторон AB и BC:
получаем 
.
Координаты вершины C получим, решая систему из уравнений сторон BC и AC:
Вершина C имеет координаты 
.
Видео:Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать
Образцы выполнения некоторых заданий
Рассмотрим решения некоторых практических упражнений.
Задание 2(е)
На плоскости даны точки А(11; -5), В(6;7), С(-10; -5). Найти уравнение биссектрисы угла А.
Решение задания 2(е)
Найдем направляющий вектор 
биссектрисы как сумму ортов векторов 
и 
,
или (умножая на 
)
.
; 
;
; 
.
.
Таким образом, в качестве направляющего вектора биссектрисы угла А можно взять вектор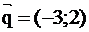 
и уравнение биссектрисы будет иметь вид
.
Задание 3
Дана точка (0;2) пересечения медиан треугольника и уравнения двух его сторон 5х – 4у + 15 = 0 и 4х + у – 9 = 0. Найти координаты вершин треугольника и уравнение третьей стороны.
Решение Координаты одной вершины найдем как координаты точки пересечения данных сторон, для чего решим систему уравнений
Получаем 
или 
Точка Оц пересечения медиан треугольника называется его центром. Отметим одно свойство центра треугольника, которое используем для нахождения координат остальных вершин:
; 
,
где хц, уц – координаты центра треугольника;
хi, yi – координаты i-ой вершины треугольника,
Для доказательства этих формул рассмотрим треугольник А1А2А3, где Аi(xi;yi), i = 1-3 (см.рис.2.1).
Рис.2.1. Вспомогательный чертеж к заданию 3
Пусть В середина стороны А1А2. Тогда А3В – медиана треугольника А1А2А3. По известному из элементарной геометрии свойству медиан треугольника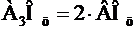 
.
Тогда координаты точки В найдем по формулам
и 
,
а координаты центра Оц из векторного соотношения 
, которое в координатной форме записывается так
, 
.
Отсюда, выражая хц и уц через xi, yi, получим требуемые формулы.
Вернемся к решению задания 3. Используя доказанные формулы, полагая в них х1 = 1 и у1 = 5, хц = 0 и уц = 2, получим два уравнения, которым должны удовлетворять координаты остальных двух вершин
; 
,
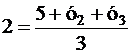
Еще два уравнения получим, если потребуем, чтобы искомые точки, вершины треугольника, принадлежали заданным сторонам, т.е. их координаты удовлетворяли уравнениям этих сторон
Итак, для определения четырех неизвестных х2, у2, х3, у3, мы имеем четыре независимых (!) условия (уравнения)
Решив эту систему, получим х2 = -3, у2 = 0, х2= 2, у3 = 1.
Наконец, уравнение третьей стороны запишем как уравнение прямой, проходящей через две заданные точки (-3;0) и (2;1)
или 
.
Итак, уравнение третьей стороны x – 5у + 3 = 0, а вершины треугольника имеют координаты (1;5), (-3;0), (2;1).
Задание 7
Составить уравнение линии, для каждой точки М которой, отношение расстояний до точки F( 
) и до прямой 
равно 
.
Привести уравнение линии к каноническому виду, определить тип линии и построить линию на чертеже. Показать на чертеже фокусы, директрисы, асимптоты (если они имеются у построенной линии).
Замечание. Отметим, что в заданиях этого модуля 
; 
; 
.
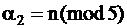
Пусть n = 101. Тогда:
, т.к. 
;
, т.к. 
;
, т.к. 
.
Итак, для n = 101 первая часть задания 7 принимает вид:
Составить уравнение линии, для каждой точки М которой, отношение расстояния до точки F(-4;1) и до прямой x = 1
равно 
.
Решение задания 7 (для n = 101).
Пусть М(х;у) произвольная точка искомой линии, r – расстояние от М до F и d – расстояние от точки М до прямой x = 1. Тогда
и 
.
По условию 
, т.е. d = 2r.
— уравнение искомой линии.
Упростим уравнение линии и приведем его к каноническому виду. Для этого возведем обе части уравнения в квадрат и выполним следующие преобразования уравнения
х 2 – 2х +1 = 4х 2 + 32х + 64 + 4(у – 1) 2 ,
3х 2 + 34х + 4(у – 1) 2 + 63 = 0,
,
.
Последнее уравнение – это каноническое уравнение эллипса с полуосями 
и 
( 
), центр которого находится в точке с координатами 
. Координаты вершин эллипса
и 
, т.е. (-9;1), 
, 
,
. Построим эллипс на чертеже (см.рис.2.2).
Рис.2.2. Эллипс с уравнением 
Фокусы эллипса имеют координаты 
, где 
.
.
Итак, координаты фокусов F1(-4;1), F2( 
;1).
Директрисы эллипса имеют уравнения 
, где е – эксцентриситет эллипса
.
Уравнения директрис 
, т.е.
D2: 
.
Отметим фокусы и директрисы эллипса на рис.2.2.
Обратите внимание на совпадение фокуса F1 с точкой, данной в условии задания 7, на совпадение директрисы D1 с прямой х = 1 из условия этого задания, и совпадение эксцентриситета е с параметром е в условии. По этому поводу см. теоретическое упражнение 18.
В пространстве даны точки А(-2; -4;1), В(3;1; -1), С(5;1;1),
S(1;-4;0). Найти координаты центра и радиус вписанной в пирамиду SABC сферы (условие сформулировано для n = 101).
Решение задания 4(м)
Пусть точка О(x0;y0;z0) – центр сферы, вписанной в пирамиду SABC. Найдем точку О как точку, равноудаленную от граней пирамиды. Для этого найдем уравнения всех граней и расстояния от точки О до этих граней (уравнения некоторых граней находятся в предшествующих пункту М пунктах задания 4).
Грань АВС. Уравнение грани
или 5х – 7у – 5z – 13 = 0.
Точки О и S лежат по одну сторону от грани АВС, поэтому отклонения этих точек от грани АВС имеют одинаковые знаки. Отклонение 
(S) точки S от грани АВС равно
> 0.
.
Аналогично все делается для граней ABS, BCS, CAS.
Грань ABS имеет уравнение 5х + у + 15z – 1 = 0 и
.
Грань BCS имеет уравнение 5х – 3у – 5z – 17 = 0 и
.
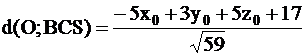
Наконец, грань CAS имеет уравнение 5х – 7у + 15z + 33 = 0 и
.
Так как О – центр сферы, вписанной в пирамиду SABC, то
d(O; ABC) = d(O; ABS) = d(O; BCS) = d(O; CAS) = r,
где r – радиус вписанной сферы.
Тогда координаты точки О должны удовлетворять системе
В отличие от других заданий этого модуля, коэффициенты и решение этой системы найдем приближенно, с помощью микрокалькулятора или ЭВМ. Получим систему
и уравнение вписанной сферы
.
1. Общее уравнение прямой на плоскости. Нормальный вектор прямой. Угол между прямыми. Условия параллельности и перпендикулярности.
2. Уравнение прямой с угловым коэффициентом. Угол между прямыми. Условия параллельности и перпендикулярности.
3. Каноническое и параметрическое уравнения прямой на плоскости. Направляющий вектор прямой. Угол между прямыми. Условия параллельности и перпендикулярности.
4. Уравнение прямой, проходящей через две заданные точки.
5. Уравнения прямых, проходящих через данную точку параллельно и перпендикулярно данной прямой (3 случая задания данной прямой: общим уравнением, каноническим уравнением, уравнением с угловым коэффициентом).
6. Общее уравнение плоскости в пространстве, нормальный вектор плоскости. Угол между плоскостями. Условие параллельности и перпендикулярности.
7. Уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой.
8. Общее, каноническое и параметрическое уравнения прямой в пространстве. Угол между прямыми. Условия параллельности и перпендикулярности.
9. Угол между прямой и плоскостью в пространстве. Условие параллельности и перпендикулярности прямой и плоскости.
10. Уравнение плоскости, проходящей через данную точку, перпендикулярно данной прямой. Уравнение прямой, проходящей через данную точку, перпендикулярно данной плоскости.
11. Расстояние от точки до: прямой на плоскости; прямой в пространстве; плоскости в пространстве.
12. Уравнение линии на плоскости. Общее уравнение кривой второго порядка.
13. Каноническое и параметрическое уравнения окружности.
14. Эллипс (фокусы и директрисы, фокальные радиусы точки, эксцентриситет). Каноническое и параметрическое уравнения эллипса.
15. Гипербола (фокусы, директрисы и асимптоты, фокальные радиусы точки, эксцентриситет). Каноническое и параметрическое уравнения гиперболы.
16. Парабола (фокус и директриса, фокальный радиус точки, эксцентриситет). Каноническое уравнение параболы.
17. Приведение общего уравнения кривой второго порядка к каноническому виду.
18. Полярные координаты на плоскости. Уравнение линии в полярных координатах.
19. Уравнение поверхности в пространстве. Общее уравнение поверхностей второго порядка.
20. Основные типы поверхностей второго порядка и их канонические уравнения.
1. Бугров Н.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1980. 176 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1: Учебное пособие для студентов втузов. – 3-е изд., перераб. и доп. – М.: Высшая школа, 1980. 320 с.
3. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1981. 232 с.
4. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1980. 240 с.
5. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа/Под ред. А.В. Ефимова, Б.П. Демидович. – М.: Наука, 1981, 464 с.
6. Высшая математика. Методические указания и контрольные задания/Под ред. Ю.С. Арутюнова. – М.: Высшая школа, 1985.
7. Гусак А.А. Пособие к решению задач по высшей математике. – Изд. 3-е. – Минск: Изд-во БГУ, 1973. 532 с.
8. Кузнецов А.А. Сборник заданий по высшей математике (типовые расчеты): Учеб. пособие для втузов. – М.: Высшая школа, 1983. 175 с.
9. Погорелов А.В.Аналитическая геометрия.– М.:Наука, 1968. 176с
Видео:Уравнения стороны треугольника и медианыСкачать
Задача 41259 Найти уравнение сторон треугольника.
Условие
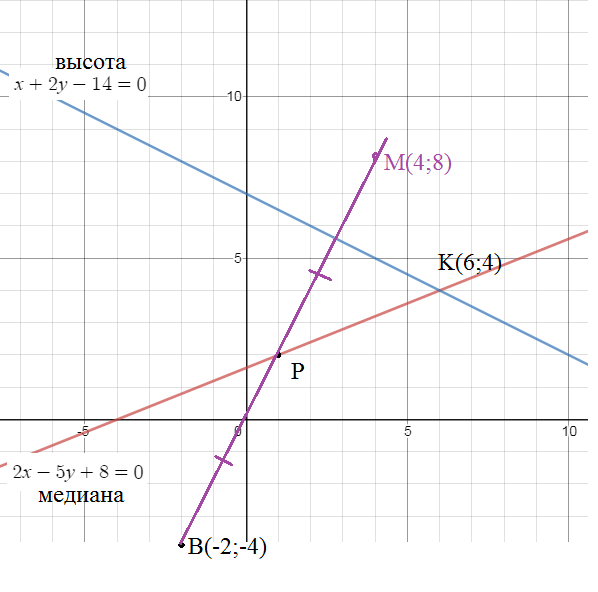
Найти уравнение сторон треугольника, если известны одна из вершин В(-2;-4) и уравнение медианы 2х-5у+8=0 и высоты х+2у-14=0 проведеденных из этой вершины
Все решения
Найдем координаты точки пересечения медианы и высоты:
<2x-5y+8=0
<x+2y-14=0
Назовем ее точка К
Скорее всего дана точка В и два уравнения медианы и высоты,
проведенных из других вершин треугольника
Составим уравнение прямой ВК, как прямой проходящей через две точки:
х+2=y+4
[b]x-y-2=0 [/b]- уравнение ВК
высота x+2y-14=0 и ВК не перпендикулярны,так как произведение угловых коэффициентов взаимно перпендикулярных прямых должно быть равно (-1).
Значит высота перпендикулярна стороне ВМ.
Координату точки М требуется найти
Уравнение стороны ВМ, как прямой, перпендикулярной x+2y-14=0
и проходящей через точку В легко написать.
Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)
Значит, угловой коэффициент стороны ВМ
k_(BM)=2
Общий вид такой прямой
y=2x+b
Так как ВМ проходит через точку В, подставим ее координаты в уравнение
y=2x+b
и найдем b
уравнение BM: [b]y=2x[/b]
Найдем координаты точки пересечения ВМ и медианы.
Решаем систему уравнений:
<2х–5у+8=0
<y=2x
Пусть это точка Р(1;2)
Уравнение КМ, как уравнение прямой проходящей через две точки:
[m]frac<x-x_><x_-x_>=frac<y-y_><y_-y_>[/m]
[b]2х+у-8=0[/b] — уравнение МК
О т в е т. x-y-2=0; y=2x; 2х+у-8=0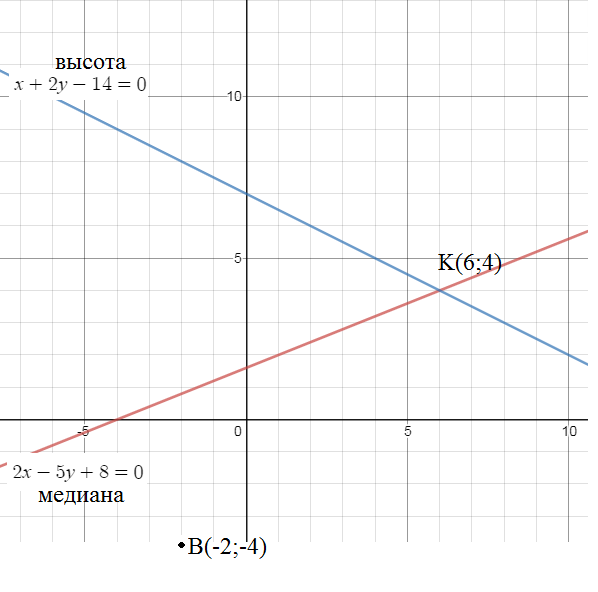 
🌟 Видео
№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать
Вычисляем угол через координаты вершинСкачать
Вычисляем высоту через координаты вершин 1Скачать
Вычисление медианы, высоты и угла по координатам вершинСкачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
найти уравнения биссектрис углов между прямымиСкачать
найти уравнение высоты треугольникаСкачать
Даны уравнения высот треуг. у=2х; у+3х+5=0 и вершина А(8; 1) Составить урав-я сторон треуг. пример 1Скачать
Аналитическая геометрия, 6 урок, Уравнение прямойСкачать
№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать
Уравнение прямой и треугольник. Задача про высотуСкачать
Математика без Ху!ни. Уравнение плоскости.Скачать
Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать
найти косинус угла С треугольника ,если даны координаты вершинСкачать
Математика без Ху!ни. Смешанное произведение векторовСкачать
Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать
№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать
Аналитическая геометрия на плоскости. Решение задачСкачать
