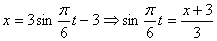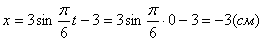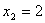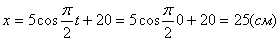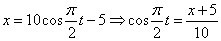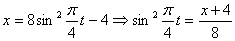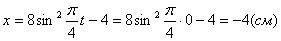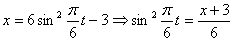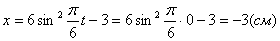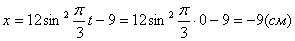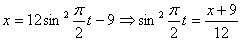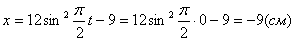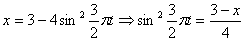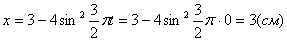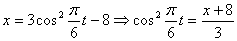Глава 7. Кинематика точки.
7.2. Скорость точки в прямоугольной системе координат.
7.2.1. Дано уравнение движения точки r = t 2 i + 2 tj + 3k. Определить модуль скорости точки в момент времени t = 2 с. (Ответ 4,47)
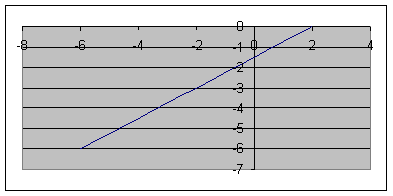
7.2.2. Дан график скорости движения точки v = f(t). Определить пройденный путь в момент времени t = 5 с. (Ответ 7,5)
7.2.3. Дан график скорости движения точки v = f(t). Определить пройденный путь в момент времени t = 60 с. (Ответ 750)
7.2.4. Даны уравнения движения точки х = t 2 , у = sin πt, z = cos πt. Определить модуль скорости точки в момент времени t = 1 с. (Ответ 3,72)
7.2.5. Скорость движения точки v = 2ti + 3j. Определить угол в градусах между вектором скорости и осью Ох в момент времени t = 4 с. (Ответ 20,6)
7.2.6. Положение линейки АВ определяется углом φ = 0,5 t. Определить в см/с проекцию скорости точки М на ось Ох в момент времени t = 2 с, если расстояние ВМ = 0,2 м. (Ответ -8,41)
7.2.7. Определить скорость точки В в момент времени t = 6 с, если расстояние ОА = 0,1 м, а угол φ = 6 t. (Ответ 0,595)
7.2.8. Положение кривошипа определяется углом φ = 0,5 t. Определить скорость ползуна В в момент времени t = 4 с, если ОА = AВ = 1,5 м. (Ответ -1,36)
7.2.9. Проекция скорости точки vx = 2 cos πt. Определить координату х точки в момент времени t = 1 с, если при to = 0 координата xо = 0. (Ответ 0)
7.2.10. Дано уравнение движения точки х = sin πt. Определить скорость в ближайший после начала движения момент времени t, когда координата х = 0,5 м. (Ответ 2,72)
Видео:Уравнение движенияСкачать
Даны уравнения движения точки x t 2 y sin p t z cos p t
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ
1.1. Даны уравнения движения точки.
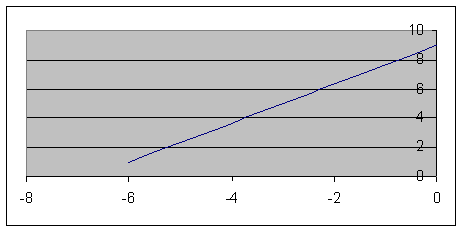
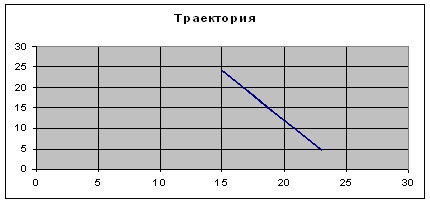
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории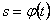 
, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: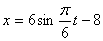 
, 
.
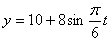
Решение: 1. Для получения уравнения траектория вида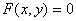 
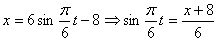
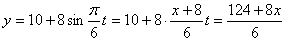
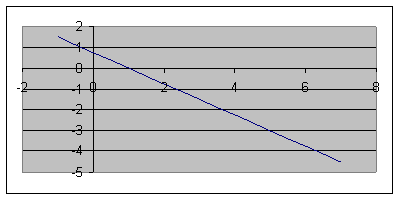
исключим из уравнений движения время t :
.
Строим уравнение траектории:
2. Для определения положения точки в начальный момент времени необходимо подставить значение 
в уравнения движения:
.
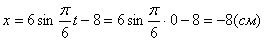
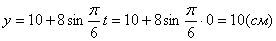
Точка при занимает положение 
.
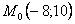
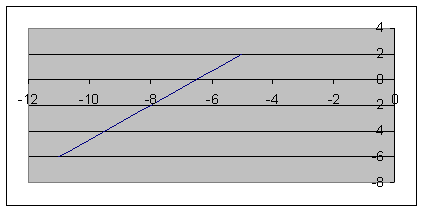
3. Так как x может принимать значения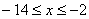 
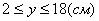
, а y 
, Пересечение с осями нет.
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при 
,
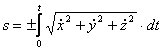
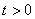
видим, что с выходом из начального положения координата х увеличивается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
.
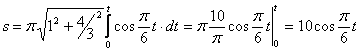
1.2. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории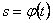 
, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: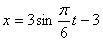 
, 
.
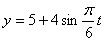
Решение: 1. Для получения уравнения траектория вида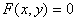 
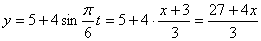
исключим из уравнений движения время t :
.
Строим уравнение траектории:
2. Для определения положения точки в начальный момент времени необходимо подставить значение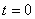 
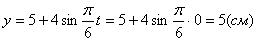
в уравнения движения:
.
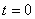
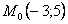
Точка при занимает положение 
.
3. Так как x может принимать значения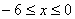 
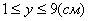
, а y 
, Пересечение с осью OX в точке (0;9).
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при 
,
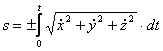
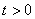
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
.
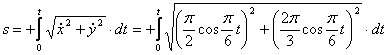
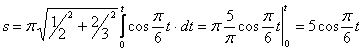
1.3. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории 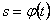, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: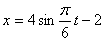 
, 
.
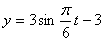
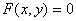
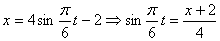
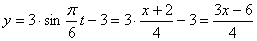
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :
.
Строим уравнение траектории:
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:
.
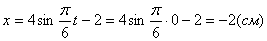
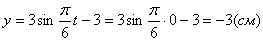
Точка при занимает положение 
.
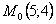
3. Так как x может принимать значения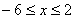 
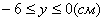
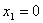
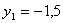
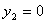
, а y 
, траектория пересекает ось ОХ при 
, 
и ось OY 
и 
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при ,
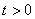
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
.
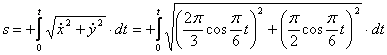
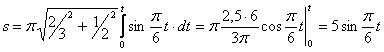
1.4. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории 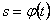, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: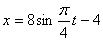 
, 
.
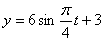
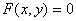
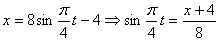
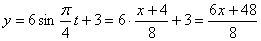
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :
.
Строим уравнение траектории:
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:
.
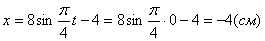
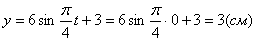
Точка при занимает положение 
.
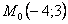
3. Так как x может принимать значения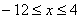 
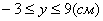
, а y 
, Пересечение с осью OX в точке (0;3,375), а с осью OY (0;-4,5).
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при ,
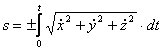
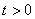
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
.
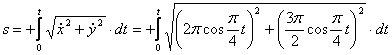
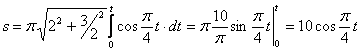
1.5. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории 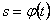, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: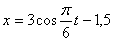 
, 
.
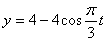
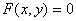
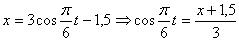
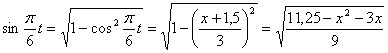
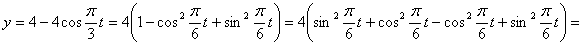
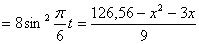
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :
,
.
Строим уравнение траектории:
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:
.
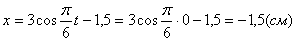
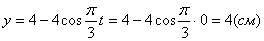
Точка при занимает положение 
.
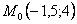
3. Так как x может принимать значения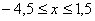 
, а y 
, Пересечение с осью OX в точке (0;-0,75) и пересечение с осью OY (-1;0).
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при ,
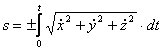
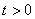
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
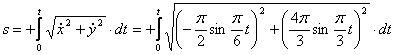
1.6. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории 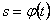, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: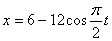 
, 
.
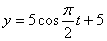
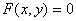
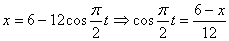
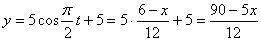
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :
.
Строим уравнение траектории:
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:
.
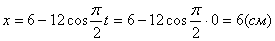
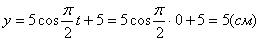
Точка при занимает положение 
.
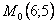
3. Так как x может принимать значения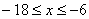 
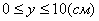
, а y 
, Пересечение с осями нет.
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при ,
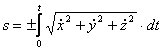
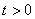
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
.
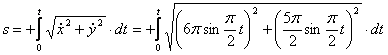
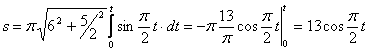
1.7. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории 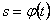, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: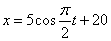 
, 
.
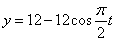
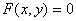
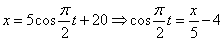
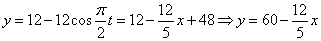
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :
.
Строим уравнение траектории:
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:
.
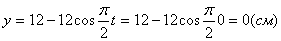
Точка при занимает положение 
.
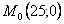
3. Так как x может принимать значения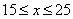 
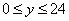
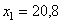
, а y 
, 
, 
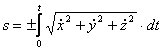
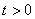
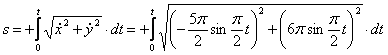
4. Для определения закона движения точки по траектории воспользуемся формулой , при , видим, что с выходом из начального положения координата х увеличивается, а координата y уменьшается. Это направление примем за положительное, тогда 
,
откуда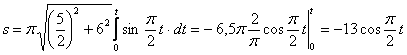 
.
1.8. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории 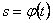, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: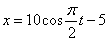 
, 
.
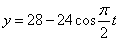
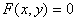
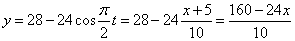
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :
.
Строим уравнение траектории:
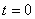
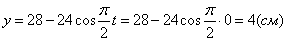
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:
.
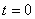
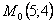
Точка при занимает положение 
.
3. Так как x может принимать значения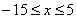 
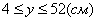
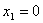
, а y 
, траектория пересекает ось ОХ при 
, 
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при ,
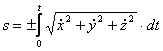
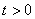
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
.
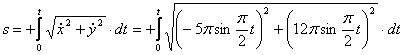
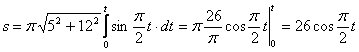
1.9. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории 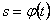, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: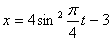 
, 
.
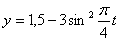
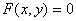
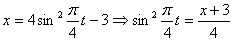
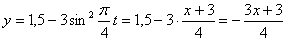
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :
.
Строим уравнение траектории:
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:
.
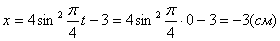
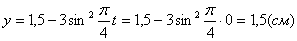
Точка при занимает положение 
.
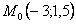
3. Так как x может принимать значения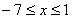 
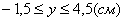
, а y 
, Пересечение с осью OX в точке (0;-0,75) и пересечение с осью OY (-1;0).
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при ,
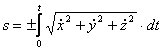
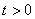
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
.
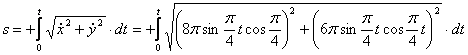
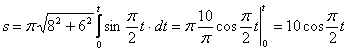
1.10. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории 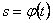, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: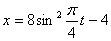 
, 
.
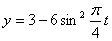
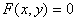
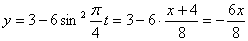
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :
.
Строим уравнение траектории:
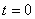
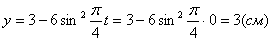
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:
.
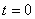
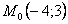
Точка при занимает положение 
.
3. Так как x может принимать значения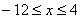 
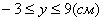
, а y 
, Пересечение с осями в точке (0;0).
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при ,
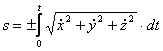
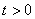
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
.
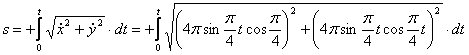
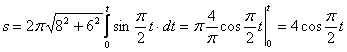
1.11. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории 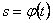, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: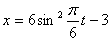 
, 
.
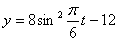
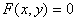
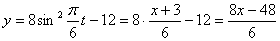
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :
.
Строим уравнение траектории:
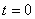
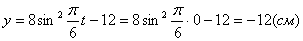
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:
.
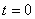
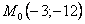
Точка при занимает положение 
.
3. Так как x может принимать значения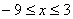 
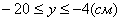
, а y 
, Пересечение с осями в точке (0;0).
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при ,
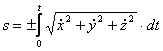
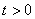
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
.
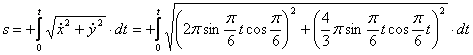
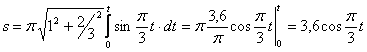
1.12. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории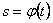 
, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: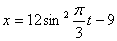 
, 
.
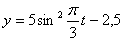
Решение: 1. Для получения уравнения траектория вида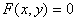 
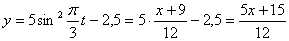
исключим из уравнений движения время t :
.
Строим уравнение траектории:
2. Для определения положения точки в начальный момент времени необходимо подставить значение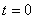 
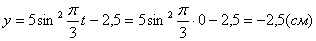
в уравнения движения:
.
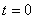
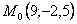
Точка при занимает положение 
.
3. Так как x может принимать значения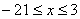 
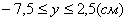
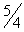
, а y 
, Пересечение с осью OX в точке (0; 
) и пересечение с осью OY (-3;0).
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при 
,
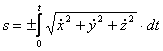
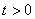
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
.
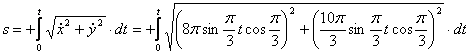
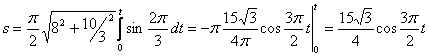
1.13. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории 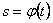, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: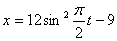 
, 
.
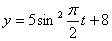
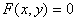
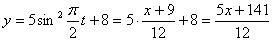
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :
.
Строим уравнение траектории:
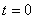
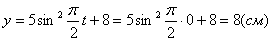
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:
.
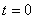
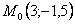
Точка при занимает положение 
.
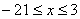
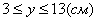
3. Так как x может принимать значения , а y 
, Пересечение с осью OY в точке (0;11,75).
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при ,
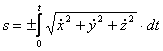
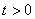
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
.
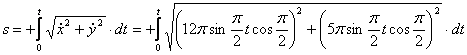
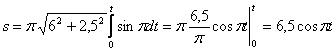
1.14. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории 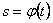, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: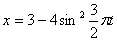 
, 
.
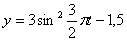
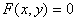
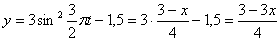
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :
.
Строим уравнение траектории:
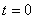
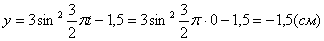
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:
.
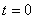
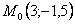
Точка при занимает положение .
3. Так как x может принимать значения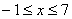 
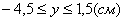
, а y 
, Пересечение с осью OX в точке (0;0,75) и пересечение с осью OY (1;0).
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при ,
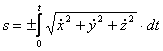
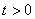
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
.
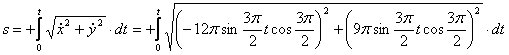
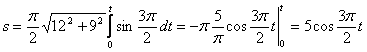
1.15. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории 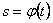, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: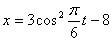 
, 
.
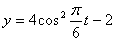
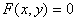
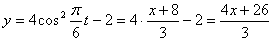
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :
.
Строим уравнение траектории:
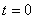
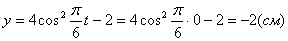
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:
.
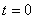
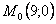
Точка при занимает положение 
.
3. Так как x может принимать значения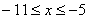 
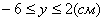
, а y 
, Пересечение с осью OX в точке (0;-6,5).
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при ,
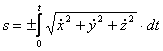
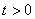
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
.
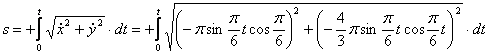
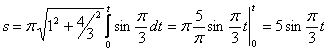
1.16. Даны уравнения движения точки.
1. Определить уравнение траектории и построить ее.
2. Определить начальное положение точки на траектории.
3. Указать моменты времени, когда точка пересекает оси координат.
4. Найти закон движения точки по траектории 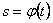, принимая за начало отсчета расстояний начальное положение точки.
5. Построить график движения точки.
Дано: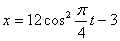 
, 
.
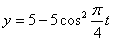
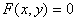
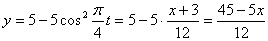
Решение: 1. Для получения уравнения траектория вида исключим из уравнений движения время t :
.
Строим уравнение траектории:
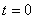
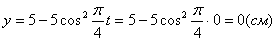
2. Для определения положения точки в начальный момент времени необходимо подставить значение в уравнения движения:
.
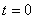
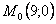
Точка при занимает положение .
3. Так как x может принимать значения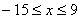 
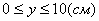
, а y 
, Пересечение с осью OX в точке (0;3,75) и пересечение с осью OY (9;0).
4. Для определения закона движения точки по траектории воспользуемся формулой:
, при ,
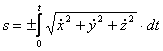
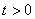
видим, что с выходом из начального положения координата х уменьшается, а координата y увеличивается. Это направление примем за положительное, тогда:
,
.
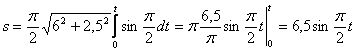
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Видео:Траектория и уравнения движения точки. Задача 1Скачать
Координатный способ задания движения точки
Рассматривается движение точки М в неподвижной системе отсчёта OXYZ (рис. 2.1). Единичные векторы (орты) i, j, k показывают положительные направления отсчёта координат X, Y, Z. Движущаяся точка описывает в пространстве некоторую линию, которую называют траекторией движения точки. По виду траектории все движения точки делятся на прямолинейные и криволинейные. Положение точки М в неподвижной системе отсчёта (НСО) определяется тремя координатами X, Y, Z. При движении точки М её координаты изменяются с течением времени. Следовательно, коорди 
наты X, Y, Z движущейся точки М являются функциями времени t.
Систему трёх уравнений X = f1(t); Y = f2(t); Z = f3(t) называют уравнениями движения точки в пространстве в декартовых координатах.
Пример: X = 10·t 2 + 1; Y = 7·t 3 + t 2 + 1; Z = 10·sin(p·t). Действительно, имея эти уравнения, можно для любого момента времени найти значения соответствующих координат X, Y, Z и по ним определить положение точки в пространстве в этот момент времени.
Движение точки М на плоскости (рис. 2.2) определяется двумя уравнениями: X = f1(t); Y = f2(t). Эти выражения называют уравнениями движения точки на плоскости в декартовой системе отсчёта.
Пример. Заданы уравнения движения точки в плоскости OXY. X = 3·t 2 + t 2 + t; Y = 7·cos(p·t).
Уравнения движения, определяющие координаты точки в любой момент времени, рассматривают как параметрические уравнения траектории точки. При исключении параметра t из уравнений движения получают уравнение траектории точки в координатной форме (Y = f(t)).
Пример. Заданы уравнения: X = 4·t (см); Y = 16·t 2 – 1 (см) движения точки в плоскости OXY. Определить вид траектории движения точки, построить её график и найти положение точки на траектории движения в момент времени t1 = 0,5 с.
Решение. Из уравнения X = 4·t находим t = X/4. Значение времени t подставляем в уравнение Y = 16·t 2 – 1. Получаем
Y = 16·(X/4) 2 – 1 = X 2 – 1.
Выражение Y = X 2 – 1 есть уравнение параболы (y= a·x 2 +b·x+c) с вершиной в точке с координатами (0, – 1). В момент времени t1 = 0,5 с определяем координаты:
Y(t1) = 16·(t1) 2 – 1 = 16·(0,5) 2 – 1 = 3 см >0.
Показываем положение точки на траектории её движения (рис. 2.3).
Пример. Дано: X = 3·sin(p·t), см (1); Y = 3·cos(p·t), см (2); t1 = 0,25 c. Определить вид траектории движения точки и её положение на траектории движения в момент времени t1.
Решение. Уравнения движения точки представим в следующем виде: (X) 2 = (3·sin(p·t)) 2 (1 I ); (Y) 2 = (3·cos(p·t)) 2 (2 I ). Для решения используем тригонометрическую формулу sin 2 (α) + cos 2 (α) = 1.
Складывая левые и правые части уравнений (1 I ) и (2 I ), получим (X) 2 + (Y) 2 = 3 2 ·(sin 2 (p·t) + cos 2 (p·t)) = 3 2 ·1 или (X) 2 + (Y) 2 = 3 2 . Известно, что уравнение (X) 2 + (Y) 2 = R 2 есть уравнение окружности радиусом R с центром в начале координат. Таким образом, точка 
движется по окружности радиусом R = 3 см (рис. 2.4).
Определяем положение точки на траектории движения в момент времени t1.
X(t1) = 3·sin(p·t1) = 3·sin(p·0,25) = 3·0,707 = 2,121 см > 0.
Y(t1) = 3·cos(p·t1) = 3·cos(p·0,25) = 3·0,707 = 2,121 см > 0.
Показываем точку на траектории её движения (см. рис. 2.4).
ВНИМАНИЕ! Если точка не попадает на траекторию её движения, то:
1) неверно определен вид траектории движения;
2) неверно рассчитаны значения координат X(t1), Y(t1).
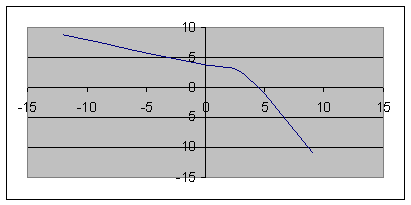
Прямолинейное движение точки М определяется одним уравнением движения X = f(t).
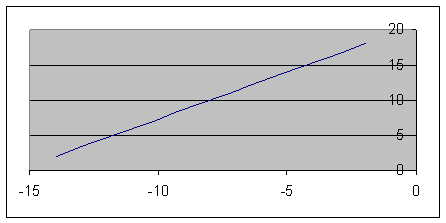
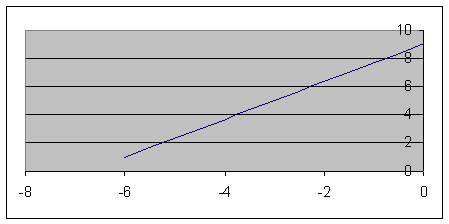
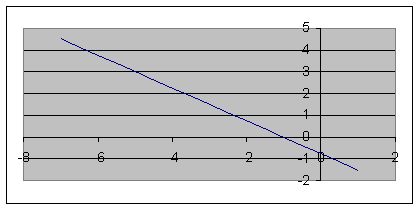
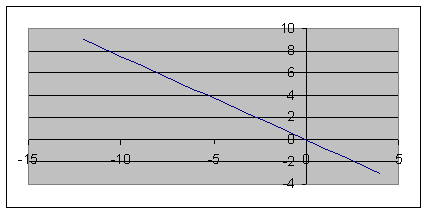
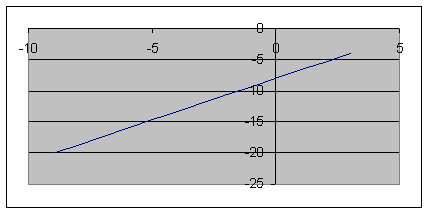
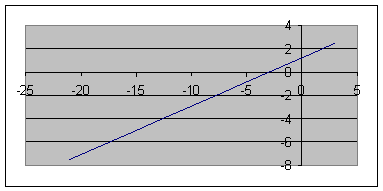
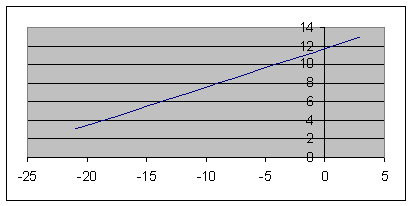
Пример. Дано: X = 10·t 2 + sin(2·p·t) + 3, см (рис. 2.5).
Определить положение точки на траектории движения в начальный момент времени t0 = 0 и в момент времени t1 = 1 c.
Решение.
X(t0) = 10·(t0) 2 + sin(2·p·t0) + 3 = 10·0 2 + sin(2·p·0) + 3 = 3 см > 0.
X(t1) = 10·(t1) 2 + sin(2·p·t1) + 3 = 10·1 2 + sin(2·p·1) + 3 = 13 см > 0.
Значения координат X(t0), X(t1) наносим на рис. 2.5.
📽️ Видео
Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать
Динамика материальной точки в НИСО. Нелинейное дифференциальное уравнение движенияСкачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Теорема об изменении количества движения точкиСкачать
Математика без Ху!ни. Непрерывность функции, точки разрыва.Скачать
Физика - уравнения равноускоренного движенияСкачать
Динамика. Введение, дифференциальные уравнения движения точки, прямая и обратная задачи динамики.Скачать
Составить уравнение прямой, проходящей через две данные точки. Метод координат. Геометрия 9 классСкачать
Кинематика точки Задание К1Скачать
Математический анализ, 5 урок, Непрерывность функцииСкачать
Векторное уравнение движения. Условие столкновения частиц: Иродов 1.5Скачать
Уравнение прямой по двум точкамСкачать
Уравнение равномерного движения. Решение задач по теме.Скачать
Уравнение прямой, проходящей через две точкиСкачать
Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.Скачать
Тригонометрические функции, y=tgx и y=ctgx, их свойства и графики. 10 класс.Скачать
Уравнение плоскости через 2 точки параллельно векторуСкачать
Видеоурок "Уравнение прямой, проходящей через две точки"Скачать
