Стороны треугольника заданы уравнениями:
Найти координаты вершин треугольника.
Координаты вершины A найдем, решая систему, составленную из уравнений сторон AB и AC:
Систему двух линейных уравнений с двумя неизвестными решаем способами, известными из элементарной алгебры, и получаем
Вершина A имеет координаты
Координаты вершины B найдем, решая систему из уравнений сторон AB и BC:
получаем 
.
Координаты вершины C получим, решая систему из уравнений сторон BC и AC:
Вершина C имеет координаты 
.
Видео:Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать
Даны уравнение стороны прямоугольника и координаты двух его вершин
Даны уравнения двух сторон параллелограмма 8х+3у+1=0, 2х+у-1=0 и уравнение одной из его диагоналей 3х+2у+3=0. Определить координаты вершин этого параллелограмма.
Выразим у:
Мы видим, что в уравнениях сторон коэффициенты при х не равны, значит прямые, определяемые этими уравнениями, не параллельны. То есть пересекаются, образуя одну из вершин. Пусть это будет вершина А. И пусть первое уравнение – сторона АВ, второе – А D .
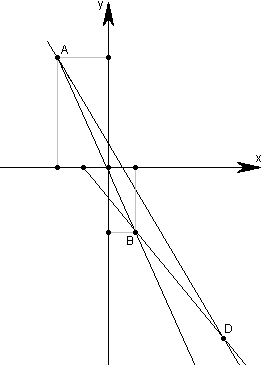
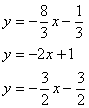
Для нахождения точки А приравняем эти два уравнения:
А(-2;5)
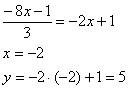
Мы видим, что уравнение 3х+2у+3=0 задает диагональ BD . Поэтому, приравняв сначала 1 и 3, а затем 2 и 3 уравнения, найдем соответственно точки D и В.
Итак В (1;-3) D (5;-9)
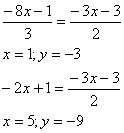
Как известно в параллелограмме противоположные стороны параллельны, то есть коэффициенты k при х равны. Поэтому для сторон ВС и CD остаются неизвестными только свободные члены d . Найдем их, подставив в уравнения прямых их известные точки D и В соответственно:
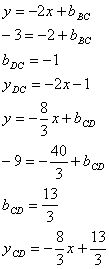
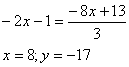
Теперь для нахождения точки С приравняем уравнения сторон BC и CD
С(8;-17)
Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать
Помогите, пожалуйста, решить задачу по геометрии.
1. Даны две противоположные вершины квадрата А (1;3) и С (-1;1). Найти коорди-наты В и D.
2.Две стороны параллелограмма заданы уравнениями у = х — 2 и 5у = х + 6. Его диа-гонали пересекаются в начале координат. Написать уравнения диагоналей.
1) Уравнение диагонали АС:
(у-ус) /(уА-уС) = (х-хС) /(хА-хС)
(у-1)/2 = (х+1)/2
у = х+2
Диагональ BD перпендикулярна АС (угловой коэффициент равен -1) и проходит через середину АС, т. е. через точку О (0;2).
Уравнение диагонали BD
y = 2 — х
Искомые координаты вершин могут быть найдены, например, из условий
АO=OВ и AO=OD
(1-0)^2 + (3-2)^2 = x^2 + (2-x-2)^2
2 = 2*x^2
x = 1; y = 2-1=1 — координаты т. В
x = -1; y = 2+1 = 3 — координаты т. D
2) Одна из вершин параллелограмма — точка пересечения данных прямых. Решение системы линейных уравнений
у = х — 2
х = 5*у — 6
даст точку вершины с координатами А (4; 2).
Начало координат — точка пересечения диагоналей, поэтому противоположная вершина С (-4; -2) — центрально симметрична точке А относительно начала координат.
Собственно, сразу можно было найти уравнение диагонали АС (то же, что и прямой АО) :
у = 2*х/4 = х/2
Для нахождения второй диагонали достаточно найти третью вершину параллелограмма, например, как точку пересечения стороны, задаваемой уравнением
х = 5*у — 6
и стороны, параллельной прямой
у = х — 2
и проходящей через точку С.
уравнение этой стороны будет иметь вид:
у = -2 + х + 4
у = х + 2
Координаты вершины В найдем из решения системы:
х = 5*у — 6
у = х + 2
Вершина В (-1; 1)
Уравнение диагонали BD (то же, что и прямой ОВ)
у = -х
🎬 Видео
Уравнения стороны треугольника и медианыСкачать
Вычисляем угол через координаты вершинСкачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Вычисляем высоту через координаты вершин 1Скачать
найти уравнение высоты треугольникаСкачать
№974. Даны координаты вершин трапеции ABCD: А (-2; -2), В (-3; 1). Напишите уравненияСкачать
Уравнение прямой и треугольник. Задача про высотуСкачать
Вычисление медианы, высоты и угла по координатам вершинСкачать
Даны уравнения высот треуг. у=2х; у+3х+5=0 и вершина А(8; 1) Составить урав-я сторон треуг. пример 1Скачать
найти уравнения биссектрис углов между прямымиСкачать
Задача, которую боятсяСкачать
№ 301-400 - Геометрия 9 класс МерзлякСкачать
№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать
Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать
Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать
Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать
№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать
Составить уравнения сторон треугольника, A(1, 2) и уравнения его высот 2x−3y+1=0 и x+y=0 пример 2Скачать
