Условие
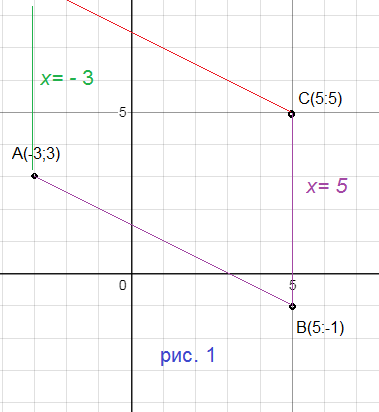
Даны три последовательные вершины параллелограмма А(-3;3), В(5;-1),С(5;5). Не находя координаты вершины D, найти:
1. найти уровень сторон AD
2. уровень высоты опущенной из вершины B на сторону AD
3. найти длину этой высоты
4. уравнение диагонали BD
5. угол между диагоналями параллелограмма
Все решения
Точки В и С имеют одинаковую первую координату, поэтому [i]уравнение прямой[/i] ВС: [red]х=5[/red]
Прямая AD || BC и проходит через точку А, у которой первая координата равна (-3)
Значит, [i]уравнение прямой[/i] АD:[red] x=-3[/red]
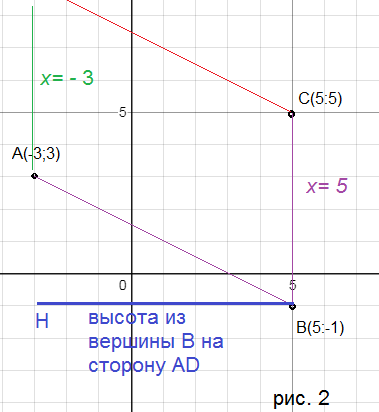
Высота ВН перпендикулярна AD и значит параллельна оси Ох.
Уравнение прямой, параллельной оси Ох и проходящей через точку В (5;-1)
y=-1
Точка Н — точка пересечения AD и BH
Значит, координаты точки H (-3;-1)
3)
[green]|BH|[/green]=[green]|x_(H)-x_(B)|[/green]=| -3 — 5|= |-8| = 8
так как это частный случай формулы
при y_(H)=y_(B)
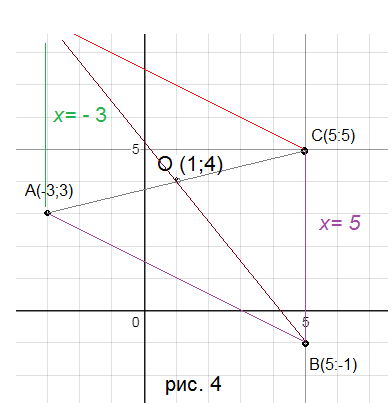
Диагонали параллелограмма в точке пересечения делятся пополам.
Координаты точки О как середины отрезка АС:
x_(O)=[m]frac<x_+x_>=frac=1[/m]
y_(O)=[m]frac<y_+y_>=frac=4[/m]
Уравнение диагонали BD — это и уравнение прямой BO.
Составим уравнение применяя общее уравнение прямой, проходящей через две точки
Пропорция, перемножаем крайние и средние члены пропорции
-5*(х-1)=4*(у-4)
-5х+5=4у-16
[b]5х+4у-21=0[/b] -[i] уравнение диагонали[/i] BD
5)
Угол между диагоналями — это меньший из углов, образованных прямыми BO и AC, значит это угол ВОС
Находим его как угол между векторами
vector и vector
Находим координаты векторов
vector=(5-1;-1-4)=(4;-5)
vector=(5-1;5-4))=(4;1)
Находим скалярное произведение векторов vector и vector
vector*vector=4*4+(-5)*1=11
|vector|=sqrt(4^2+(-5)^2)=sqrt(41)
|vector|=sqrt(4^2+1^2)=sqrt(17)
сos ( ∠ vector, vector)=[m]frac<sqrtcdot sqrt>=frac<sqrt>=frac<11sqrt>[/m] 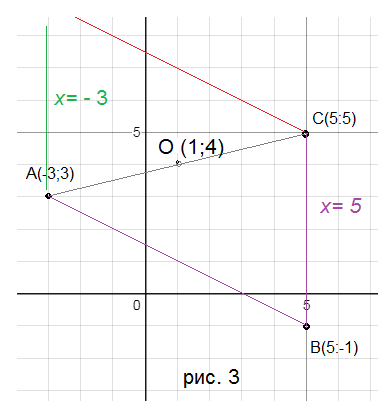
Видео:Уравнения стороны треугольника и медианыСкачать

Даны три последовательные вершины параллелограмма не находя вершину д найти уравнение стороны ад
Ответ:
Подразумевая, что задача для 7-ого/8-ого класса попробую решить ее наиболее понятным для Вас и подробным способом:
1) По определению параллелограмма сторона AD будет параллельна стороне BC. Мы знаем, что параллельные прямые имеют одинаковый коэффициент k (то есть у них одинаковый тангенс угла наклона).
Воспользуемся этим и зададим уравнение прямой BC.
Это проще всего сделать по формуле:
Однако Вам может быть этот способ непривычен.
Тогда составляете систему из двух уравнений, как Вас учили и приходите к тому же самому выводу.
Обратимся теперь к уравнению . Наша прямая проходит через точку A(3; -2). Тогда . Коэффициент мы нашли.
Подставим эти данные в уравнение и получим . Тогда искомое уравнение .
2) Прямая BK по определению высоты перпендикулярна стороне AD. Мы знаем, что в этом случае выполняется свойство . Тогда . Прямая проходит через точку B(1; -1). Тогда коэффициент будет равен , а все уравнение имеет вид .
3) Длина высоты BK может быть получена, например путем решения системы из уравнений, записанных в пунктах 1 и 2. Но ответ будет кривой. Подобную операцию вы всегда сможете сделать сами, а я позволю себе отойти немного в сторону.
Тогда . Так считать намного проще.
4) Точку D здесь использовать не запрещается. D(2, 4). Откуда уравнение будет .
Видео:Найдите вершину A параллелограмма ABCD, если B(3; −4; 7), C(−5; 3; −2) и D(1; 2; −3)Скачать

Даны три последовательные вершины параллелограмма А(1 2) В(-2
Даны три последовательные вершины параллелограмма А(1;2), В(-2;1),С(-4;-5). Не находя координаты вершины D, найти:
уравнение стороны AD;
уравнение высоты BK, опущенной из вершины В на сторону AD;
длину высоты BK;
уравнение диагонали BD;
тангенс угла между диагоналями параллелограмма.
Записать общие уравнения найденных прямых. Построить чертеж.
) Найдем уравнение прямой BC по формуле уравнения прямой, проходящей через две точки А1 и А2:
x-x1x2-x1 = y-y1y2-y1.
x+2-4+2 = y-1-5-1⇒x+22 = y-16⇒3x+6=y-1⇒y=3x+7.
Получили уравнение вида y=kx+b – уравнение с угловым коэффициентом, k=3.
Так как противоположные стороны параллелограмма параллельны, то искомое уравнение прямой AD будем искать как уравнение прямой, проходящей через точку A параллельно прямой BC. Угловые коэффициенты у параллельных прямых одинаковые.
Уравнение прямой, проходящей через данную точку Mx0;y0 в данном направлении, имеет вид:
y-y0=kx-x0.
Тогда уравнение стороны AD имеет вид:
y-2=3x-1⇒3x-y-1=0.
2) Составим уравнение высоты BK, проведенной из вершины B на сторону AD как уравнение прямой, проходящей через точку B перпендикулярно прямой AD.
Из условие перпендикулярности двух прямых: k=-13.
y-1=-13x+2⇒3y-3=-x-2⇒x+3y-1=0.
3) Найдем длину высоты BK по формуле длины перпендикуляра, опущенного из точки B на прямую AD:
d=Ax0+By0+CA2+B2, где A=3, B=-1.
d=3∙-2-1-132+-12=810.
4) Найдем уравнение диагонали BD как уравнение прямой, проходящей через точки B и E, где E – середина отрезка AC.
Если A(x1, y1), C(x2, y2), то координаты точки Ex0;y0 – середины отрезка AC, определяются формулами:
x0=x1+x22; y0=y1+y22.
x0=1-42=-32; y0=2-52=-32.
x+2-32+2 = y-1-32-1⇒x+212 = y-1-52⇒-5x+2=y-1⇒5x+y+9=0.
5) Найдем уравнение диагонали AC как уравнение прямой, проходящей через две данные точки:
x-1-4-1 = y-2-5-2⇒x-15 = y-27⇒7x-7=5y-10⇒7x-5y+3=0,
уравнение с угловым коэффициентом имеет вид y=75x+35, угловой коэффициент k1 прямой AC равен 75.
Уравнение диагонали BD имеет вид 5x+y+9=0, уравнение с угловым коэффициентом имеет вид: y=-5x-9, k2=-5.
Тангенс угла φ между прямыми с угловыми коэффициентами k1 и k2 определяется формулой:
tgφ=k2-k11+k1k2.
Следовательно,
tgφ=-5-751+75∙-5=3256=1615⇒φ≈470.
Построим чертеж:
-3238595250
Ответ. 1) 3x-y-1=0; 2) x+3y-1=0; 3) 810; 4) 5x+y+9=0; 5) 470.
Контрольная работа № 4
Вычислить пределы функций.
а) limx→∞x3-4×2+63×3+10×2+4x=∞∞=limx→∞x31-4x+6x33x31+103x+43×2=limx→∞x33x3=13.
Пределы от функций:-4x, 6×3, 103x и 43×2 равны 0 при x→∞.
б) limx→53×2-14x-5×2-6x+5=00=limx→53x+1x-5x-1x-5=limx→53x+1x-1=164=4;
limx→13×2-14x-5×2-6x+5=limx→13x+1x-1=40=+∞.
в)limx→-23x-6+2×3+8=00=
=limx→-23x-6+23x-62-23x-6+4x+2×2-2x+43x-62-23x-6+4=
=limx→-2x-6+8x+2×2-2x+43x-62-23x-6+4=
=limx→-21×2-2x+43x-62-23x-6+4=
=14+4+4364-23-8+4=112∙4+4+4=1144.
г)limx→01-cos5xxtg2x=limx→02sin25x2xsin2xcos2x=limx→02sin5x25x22∙25×24∙cos2xx∙sin2x2x∙2x=
=limx→02∙25×24∙cos2x2x2=254.
limx→0sin5x25x2=y=5×2=limy→0sinyy=1-первый замечательный предел;
limx→0sin2x2x=y=2x=limy→0sinyy=1-первый замечательный предел.
д)limx→π4tgπ4-xtg2x=0∙∞=y=π4-x⇒x=π4-y;y→0 при x→π4=
=limy→0tgy∙tgπ2-2y=limy→0tgy∙tgπ2-2y=limy→0tgy∙ctg2y=
=limy→0tgytg2y=limy→0tgyy∙ytg2y2y∙2y=limy→0y2y=12.
limx→0tgyy=limx→0tg2y2y=1-следствие из первого замечательного предела.
е) limx→∞13x+213x-15x+7=1∞=limx→∞13x-15+15+213x-15x+7=
=limx→∞1+1713x-15x+7=limx→∞1+1713x-1513x-1517 ∙ 1713x-15 ∙ x+7=
=elimx→∞ 1713x-15 ∙ x+7=e1713;
limx→∞1+1713x-1513x-1517 =y=13x-1517;y→∞ при x→∞=limy→∞1+1yy =e-
второй замечательный предел.
limx→113x+213x-15x+7=15-28=7,58.
Контрольная работа № 5
Производная и дифференциал
1. Найти производные:
а) y=10×5-14×4=10×5-x-44;
y’=10∙5×5-1–4∙x-4-14=50×4+1×5.
б) y=13xsinx=x-13sinx;
y’=-13x-13-1sinx+x-13cosx=-13x3xsinx+13xcosx=
=13xcosx-sinx3x.
в) y=tgxx;
y’=xcos2x-tgx2xx=xcos2x-sinx2xcosxx=2x-sinxcosx2xcos2xx=4x-sin2x4xxcos2x.
г) y=cosx1-sinx;
y’=-sinx1-sinx-cosx∙-cosx1-sinx2=-sinx+sin2x+cos2x1-sinx2=
=1-sinx1-sinx2=11-sinx.
д) y=ln1-ctgx;
y’=1sin2x1-ctgx=1sin2x-sin2x∙cosxsinx=1sin2x-sinx∙cosx=
=22sin2x-sin2x.
е) y=e-x+10lnx
y’=-e-x+10lnxln10x.
ж) y=arctg1+x1-x
y’=11+1+x1-x2∙1-x+1+x1-x2=21+1+x21-x21-x2=
=21-x2+1+x2=21-2x+x2+1+2x+x2=22×2+2=1×2+1.
з) y=sin23xcos32x;
y’=2sin3x∙cos3x∙3cos32x+sin23x3cos22x∙-sin2x∙2=
=3sin6xcos32x-6sin23xcos22x∙sin2x.
и) y=arcsinex+arccos12x=arcsinex+arccos2-x;
y’=11-e2xex-11-2-2×2-xln2∙-1=ex1-e2x+ln22x1-2-2x=
=ex1-e2x+ln222x-1.
к) y=tg3lnx;
y’=1cos23lnx∙3lnxln3x=3lnxln3xcos23lnx.
л) y=xx+1x-2;
y’=x+1x-2+x2x+1x-2∙12xx-2-12xx+1x-22=
=x+1x-2+x-2x+1∙xx-2-x-14x-22=
=x+1x-2-x-2x+1∙3x4x-22.
м) y=arctgx2-lnsinx;
y’=11+x4∙2x-cosxsinx=2×1+x4-ctgx.
2. Найти dydx
а) xy=lnex+y-2-функция выражена неявно.
y+xy’=ex+y∙y’ex+y-2; yex+y-2+xy’ex+y-2=ex+y∙y’;
yex+y-2=ex+y-xex+y-2y’;y’=yex+y-2ex+y-xex+y-2.
dydx=y’=yex+y-2ex+y-xex+y-2.
б) tgy-1=x+y2-функция выражена неявно.
y’cos2y-1=1+2yy’; y’cos2y-1-2yy’=1;
1-2ycos2y-1cos2y-1y’=1;y’=cos2y-11-2ycos2y-1;
dydx=y’=cos2y-11-2ycos2y-1.
в) x=arctgty=t2+1.
Используем формулу:
dydx=y’tx’t=2t2t2+111+t2=tt2+1.
3. Найти d2ydx2:
y=x3x-1.
dydx=y’=3x2x-1-x3x-12=x23x-3-xx-12=2×3-3x2x-12.
d2ydx2=y”=6×2-6xx-12-2x-12×3-3x2x-14=
=x-16xx-12-22×3-3x2x-14=
=6xx2-2x+1-4×3+6x2x-13=6×3-12×2+6x-4×3+6x2x-13=
=2×3-6×2+6xx-13=2xx2-3x+3x-13.
🎬 Видео
№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Задача по аналитической геометрииСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Вычисление медианы, высоты и угла по координатам вершинСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Уравнение прямой и треугольник. Задача про высотуСкачать

найти уравнение высоты треугольникаСкачать

Аналитическая геометрия на плоскости. Решение задачСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Уравнение плоскости через 3 точкиСкачать

Уравнение окружности (1)Скачать

8 класс, 4 урок, ПараллелограммСкачать

Уравнения прямой на плоскости | Векторная алгебраСкачать