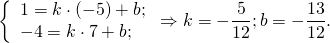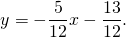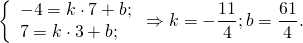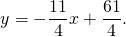Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
Видео:№768. Точки М и N — середины сторон АВ и АС треугольника ABC. Выразите векторыСкачать
Даны середины сторон треугольника составить уравнения сторон этого треугольника
Как известно общий вид уравнения прямой в плоскости – у = kx + b
Из этого уравнения следует, что для того, чтобы найти уравнение прямых содержащих стороны, необходимо знать:
Коэффициент k равный тангенсу угла между прямой и положительным направлением оси О х
Число b – свободный член или координата у в тот момент, когда прямая пересекает ось Оу
Для нахождения этих параметров определим координаты вершин треугольника:
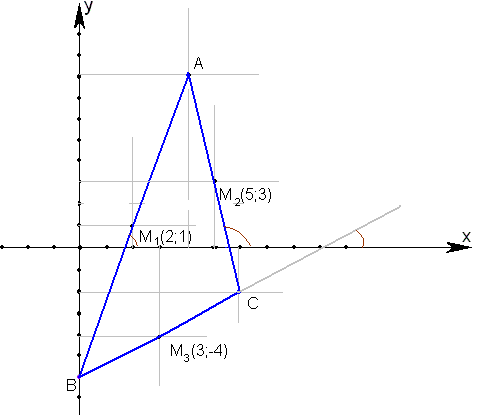
Пусть точка М 1 – середина стороны АВ, М2 – АС и М3 – ВС, тогда по формуле середины отрезка составляем уравнения
откуда определяем координаты вершин А (4;8) В( 0;-6) и С (6;-2)
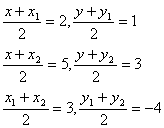
Соединим вершины и выделим углы, тангенсы которых нам необходимо найти.
Введем следующие обозначения:
Прямая, содержащая сторону 1) АВ – у 1 = k 1 x + b 1
Составим два уравнения соответственно для точек А и точки В
Составим два уравнения соответственно для точек А и точки C
Составим два уравнения соответственно для точек C и точки В
Видео:Уравнения стороны треугольника и медианыСкачать
Задача 26413 4.1.25) Даны середины сторон.
Условие
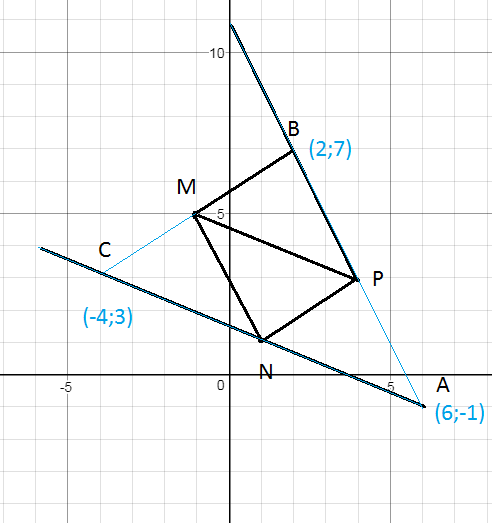
4.1.25) Даны середины сторон треугольника M (-1; 5), N( 1; 1), P(4; 3).
Найти координаты его вершин.
Решение
Уравнение прямой MN:
(х–x_(M))/(x_(N)–x_(M))=(y–y_(M))/(y_(N)–y_(M))
MN- средняя линия треугольника, параллельна стороне.
Пусть это сторона АВ. Тогда уравнение прямой АВ имеет вид
у=-2х+b
Для нахождения b подставляем координаты точки P(3;4)
3=-2*4+b
b=11
y= — 2x +11
Аналогично находим уравнение прямой
MP:
(x+1)/(4+1)=(y-5)/(3-5) ⇒ y=(-2/5)x+(23/5)
Уравнение прямой AС имеет вид у=(-2/5)х+p
Подставляем координаты точки N
1=(-2/5)+p
p=7/5
Находим точку пересечения прямых АВ и AС
Решаем систему
<y= — 2x +11
<у=(-2/5)x+(7/5)
Уравнение прямой ВС имеет вид у=(2/3)х+q
Подставляем координаты точки M
5=(2/3)*(-1)+q
q=17/3
Находим точку пересечения прямых АВ и ВС
Решаем систему
<y= — 2x +11
<у=(2/3)x+(17/3)
C(-4;3)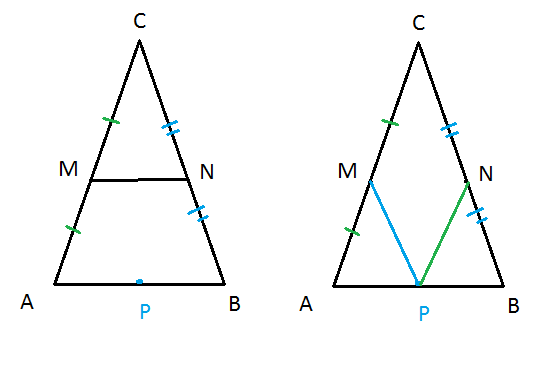 
💡 Видео
№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать
№163. Докажите, что середины сторон равнобедренного треугольника являются вершинами другого равнобедСкачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Вычисляем высоту через координаты вершин 1Скачать
В треугольнике отмечены середины M и N сторон BC и AC ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать
Координаты середины отрезкаСкачать
найти уравнения биссектрис углов между прямымиСкачать
Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать
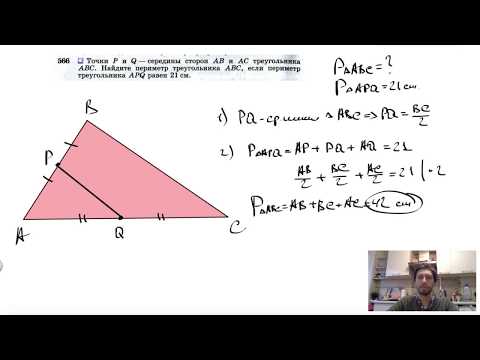
№566. Точки Р и Q — середины сторон АВ и АС треугольника ABC. Найдите периметр треугольникаСкачать
ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать
Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать
Найдите третью сторону треугольникаСкачать
Вычисление медианы, высоты и угла по координатам вершинСкачать
Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать
7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать
Задача про соотношение сторон. Геометрия 7 класс.Скачать
Координаты середины отрезка. Практическая часть. 11 класс.Скачать
Нахождение стороны прямоугольного треугольникаСкачать
