 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 |
1. Даны результаты прямых измерений некоторых физиичес-ких величин и уравнение их связи с другой физической величиной.
2. Найти значение этой величины и оценить его погрешность.
Окончание табл. З.10
Полученные в процессе выполнения расчетно-графических работ навыки и знания обработки данных измерений какой-либо величины позволяют студенту научиться анализировать производственный процесс и принимать правильные решения на последующие действия.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Брянский, справочник метролога / , . – М.: Издательство стандартов. 1991. – 79 с.
2. Кушнир, / , . – Л.: Энергия, 1975. – 368 с.
3. Тейлор, Дж. Введение в теорию ошибок / Дж. Тейлор. – М.: Мир, 1985. – 272 с.
4. Сквайрс, Дж. Практическая физика / Дж. Сквайрс. – М.: Мир, 1971. – 248 с.
5. Худсон, Д. Статистика для физиков / Д. Худсон. – М.: Мир, 1970. – 298 с.
6. Кунце, физических измерений / . – М.: Мир, 1989. – 216 с.
7. Тойберт, П. Оценка точности результатов измерений / П. Тойберт. – М.: Энергоатомиздат, 1988. – 88 с.
8. Крылова, стандартизации, сертификации, метрологии / . – М.: ЮНИТИ, 2001. – 711 с.
9. Сертификация: учеб. пособие / [и др.]. 1999. – 89 с.
10. Метрология, стандартизация и сертификация: учеб. пособие / [и др.]. 2002. – 278 с.
11. Артемьев, пособие для работников метрологических служб: в 2-х кн. Кн. 1 / , . – М.: Изд-во стандартов, 1990. – 582 с.
12. Кузнецов, распределения погрешностей измерений с учетом времени эксплуатации измерительных приборов / , . – Измерительная техника. – 1992. – № 7.
13. Кузнецов, метрологии / , . – М.: ИПК Изд-во стандартов, 1995. – 278 с.
14. Маркин, по метрологии / . – М.: Изд-во стандартов, 1994. – 188 с.
15. Савчук, результатов измерений. Физическая лаборатория. В 2-х. Ч1: учеб. пособие для студентов вузов / . – Одесса: ОНПУ, 2002.
1. Виды измерений. Классификация погрешностей…..……
2. Обработка прямых измерений…………………….………
2.1. Инструментальная погрешность………….…………
2.2. Случайная погрешность……. ………………………
3. Обработка косвенных измерений……..…………… ….…
4. Правила округления приближенных чисел……..… …
4.1. Округление погрешности действительного значений…………………………………………………………….
4.2. Запись чисел, считанных со шкалы прибора….……
4.4. Округление при вычислениях………………….……
5. Примеры обработки результатов измерений…………
5.1. Примеры обработки прямых измерений…… ………
5.2. Примеры объединения результатов прямых измерений………………………………………………… ……….
5.3. Примеры обработки результатов косвенных измерений………………………………………………… ……….
6. Вероятностные свойства серии наблюдений…… ………
6.1. Определение основных понятий…………… ………
6.2. Нормальное распределение………………… ………
7. Краткие теоретические сведения по определению абсолютной, относительной и приведенной погрешностей измерения………………………………………………… …….
8. Пример выполнения задания № 1…………..…… ………
9. Пример выполнения задания № 2……………….… …….
Список использованной литературы.………………. ……..
Николай Иванович Привалов
Александр Александрович Шеин
Надежда Васильевна Бережная
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ И
ОПРЕДЕЛЕНИЕ погрешностЕЙ измерений
Темплан 2011 г., поз. № 6К.
Подписано в печать г. Формат 60×84 1/16.
Бумага листовая. Печать офсетная.
Усл. печ. л. 3,95. Уч.-изд. л. 3,64
Тираж 100 экз. Заказ №
Волгоградский государственный технический университет
Видео:Урок 3. Погрешность прямых измеренийСкачать

Примеры решения типовых задач
Примеры выполнения практических заданий
Пример 1.При проведении измерительного эксперимента получены следующие значения величины: 11,65; 11,41; 11,57; 11,60; 11,50; 11,55; 11,58; 11,58; 11,61; 11,63. Требуется проанализировать полученные результаты наблюдений в целях выявления грубых погрешностей, используя критерий Диксона.
1. Располагаем результаты наблюдений в вариационный возрастающий ряд:
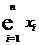
5. Находим среднеквадратическое отклонение среднего арифметического результата наблюдения по формуле
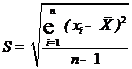
Разность хi –  | Квадрат разности | 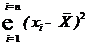 |
х1—  =9,39-9,44=-0,05 =9,39-9,44=-0,05 | 0,0025 | 0,0118 |
х2—  =9,40-9,44=-0,04 =9,40-9,44=-0,04 | 0,0016 | |
х3—  =9,41-9,44=-0,03 =9,41-9,44=-0,03 | 0,0009 | |
х4—  =9,42-9,44=-0,02 =9,42-9,44=-0,02 | 0,0004 | |
х5—  =9,43-9,44=-0,01 =9,43-9,44=-0,01 | 0,0001 | |
х6—  =9,46-9,44=0,02 =9,46-9,44=0,02 | 0,0004 | |
х7—  =9,47-9,44=0,03 =9,47-9,44=0,03 | 0,0009 | |
х8—  =9,49-9,44=0,05 =9,49-9,44=0,05 | 0,0025 | |
х9—  =9,49-9,44=0,05 =9,49-9,44=0,05 | 0,0025 |
Определяем число степеней свободы f=n-1=9-1=8
Рассчитываем стандартное отклонение:

6. Подставляем полученные расчетные данные в основную формулу (14):
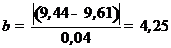
7. Находим табличное значение критерия Романовского 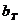
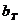
8. Вывод: рассчитанное значение 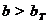
Ответ:Так как 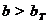
Пример 3. Некоторую физическую величину измерили двумя независимыми способами. По первому способу получили результаты:38.20,38.00,37.66; по второму – 37.70,37.65,37.55. Значимо ли различаются результаты данных измерений?
1. По формуле (6) рассчитаем среднее арифметическое значение для каждого способа:
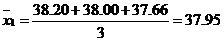
2. Рассчитаем дисперсии 
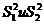
3. Проведем сравнение точности обоих методов, используя F-распределение:
Fэксп =
Полученные значения Fэксп, сопоставляем с табличным (таблица 6, приложения 3) значением F распределения при р=0.95 и числах степеней свободы f 1 =2 и f 2 =2.
Так как F табл= 19.00> F эксп=12.78, то расхождение между дисперсиями незначимо и, следовательно, способ измерения физической величины одинаковой точности.
С помощью t-критерия оцениваем расхождение между 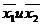
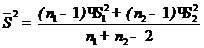
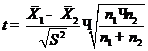
t эксп =
Сопоставляем полученное значение t эксп с табличными t 0.95;4 = 2,776 (при р= 0,95 и f = 3+3-2=4). Так как t эксп =1.96 3 .
1.Среднее арифметическое значение вычисляем по формуле (6):
2.Стандартное отклонение отдельного определения вычисляем по формуле (9):
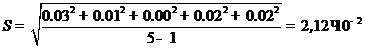
3.Из формулы (15) находим значение величины t:
Из таблицы значений коэффициента Стьюдента (смотри таблицу 1 приложения 3) для f=4 и p=0,95, tр,f=2,78, что больше рассчитанного из формулы (15) 
Ответ. Следовательно, средняя величина 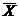
Пример 6. При определении коэффициента теплопроводности 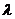
1. По формуле (6) находим среднее арифметическое значение:
2.Стандартное отклонение единичного результата вычисляем по формуле (9):
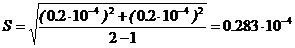
По таблице 1 приложения 3 находим для р=0.95 и f=2-1=1 tр,f=12.7 и по формуле (15) вычисляем точность метода:
3. Определяем относительную точность измерения по формуле (22):
Если необходимо получить D=5%, то
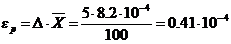
Если принять n=4, то t=2.90. Исходя из данных таблице 1 (см. приложение 3) для р=0.95 и f=4–1=3 tр,f=3.18, что не обеспечивает точности 5%. Если принять n=5, то t=3.24. По таблице 1 (см. приложение 3) для р=0.95 и f=5–1=4 tр,f=2.78, что меньше рассчитанного t=3.24. Следовательно, при n=5 величина t=3.24 дает большую вероятность, чем 0.95.
Ответ. Для достижения относительной погрешности 5% необходимо провести 5 измерений. Так как n 0.50, то выбрать другой закон распределения и снова применить к нему критерий согласия Пирсона. Если при исследовании гипотез о трех различных распределениях (нормальном, логарифмическом и распределении Вейбулла) вероятность несогласования р>0.50, то выбрать лучшее по вероятности распределения.
4. Найти доверительный интервал для математического ожидания M(X)=m и среднего квадратичного отклонения s(X)=s, если задан уровень значимости q, полученной в пункте 3 при выборе распределения величины Х.
1. Исследуем данную выборку на однородность. Для этого все результаты измерений расположим в порядке возрастания. Результат запишем в виде табл. 1.
По условию требуется проверить, не содержит ли данная выборка грубых ошибок на уровне значимости 0.05, то есть из выборки следует исключить те хi, которые с вероятностью 1–q=0.95.
Найдем критическое значение числа
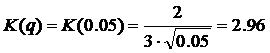
с которым будем сравнивать максимальное отклонение t(xi). Нанесем на ось все значения из табл. 6.1.
Табл. 6.1. Экспериментальные значения величины Х
| I | xi | i | xi | i | xi | i | xi |
| 117.17 118.40 118.49 118.73 118.88 119.00 119.00 119.01 119.18 119.22 119.31 119.34 119.35 119.36 119.37 119.37 119.39 119.42 119.43 119.43 119.54 119.55 119.55 119.56 119.56 | 119.57 119.58 119.59 119.61 119.62 119.65 119.72 119.75 119.76 119.83 119.85 119.85 119.90 119.91 119.91 119.92 119.92 119.95 119.95 119.96 119.99 120.02 120.03 120.06 120.06 | 120.06 120.07 120.10 120.13 120.16 120.16 120.17 120.20 120.25 120.31 120.45 120.50 120.51 120.52 120.53 120.57 120.59 120.62 120.63 120.71 120.76 120.80 120.82 120.84 120.86 | 120.87 120.89 120.90 120.90 121.03 121.07 121.11 121.11 121.19 121.25 121.31 121.35 121.39 121.46 121.47 121.64 121.66 121.68 121.76 121.84 121.92 122.21 122.21 |
Рис. 6.1. Распределение случайной величины
Как можно видеть из рис. 6.1, наиболее густо точки расположены в интервале [119, 122]. Значение x1=117.17 резко отличается от интервала [119, 122], что может служить косвенным подтверждением того, что величина x1 является грубой ошибкой. Остальные значения xi не вызывают особых подозрений, поэтому мы исследуем дополнительно крайние точки x1, x2, x97 и x98.
Временно отбросив указанные значения, подсчитаем среднее арифметическое значение и эмпирический стандарт:
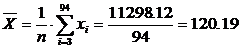
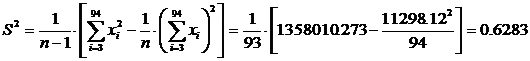
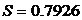
Исследуем сначала x1=117.17, применив к нему наш критерий. Оказалось, что 
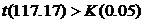
Применим t-критерий к значению x2=118.40. Расчет значения t-критерия дает следующую величину 
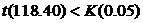
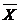
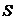
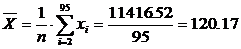

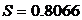
Вычислим 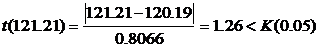
Для полученной выборки находим
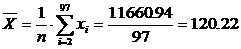
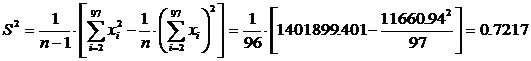
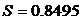
2. Сгруппируем данные табл. 6.1 по интервалам с шагом, вычисленным по соотношению
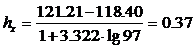
Начальная точка равна 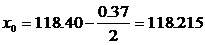
Найдем границы интервалов 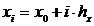
По данным табл. 6.2 построим гистограмму. Для этого отложим на оси х интервалы длиной 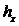
Табл. 6.2. Расчет высоты прямоугольников для построения гистограммы
| I | Интервал xi | Число попаданий в i-ый интервал | 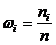 | 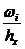 |
| 118.215 118.585 118.955 119.325 119.695 120.065 120.435 120.805 121.175 121.545 121.915 122.285 | 0.0206 0.0206 0.0619 0.2062 0.2062 0.0928 0.1237 0.1134 0.0722 0.0515 0.0309 | 0.0557 0.0557 0.1673 0.5573 0.5573 0.2508 0.3343 0.3065 0.1951 0.1392 0.0835 |
3. Предположим, что случайная величина распределена по нормальному закону распределения с параметрами 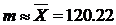

Результаты вычислений занесем в табл. 6.3.
Для заполнения табл. 6.3 в столбец 2 занесем из табл. 6.2 концы интервалов xi; затем заполняем столбец 3 по формуле 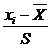
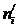

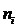
Для расчета критерия Пирсона объединим первые и последние два интервала. Используя данные табл. 6.3, рассчитаем критерий согласия Пирсона 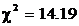
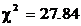
Составим уравнение прямой, проходящей через точки с этими координатами: 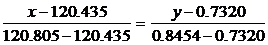
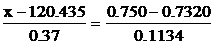
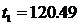
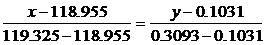
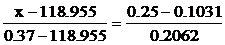
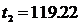
Затем найдем оценки параметров 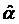
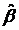
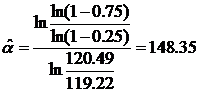
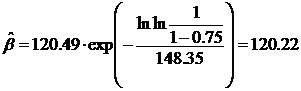
Таким образом, предполагаемая функция плотности вероятности имеет вид

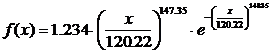
Проверим, насколько это распределение Вейбулла согласуется с истинным распределением, используя критерий согласия Пирсона. Для расчета критерия Пирсона объединим первый и второй интервалы и восьмой–одиннадцатый интервалы. Результаты вычислений заносим в табл. 6.4: 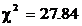
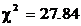
Выдвинем гипотезу о логарифмически нормальном распределении. Оценим параметры этого распределения по формулам (58) и (59). Находим, что
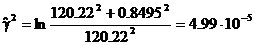
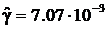
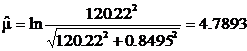
Тогда предполагаемая функция вероятностей имеет вид
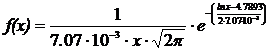
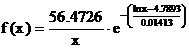
Сделаем проверку гипотезы о логарифмически нормальном распределении по критерию согласия Пирсона (табл. 4 приложения 3).
Как можно видеть, значение критерия 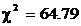
Табл. 6.5. Проверка гипотезы о логарифмически нормальном распределении величины Х
| i | xi | 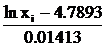 | 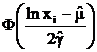 | pi | 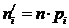 | 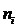 |
| 118.215 118.585 118.955 119.325 119.695 120.065 120.435 120.805 121.175 121.545 121.915 122.285 | – –0.9674 –0.7467 –0.5272 –0.3081 –0.0896 0.1281 0.3452 0.5616 0.7774 0.9925 + | –0.5000 –0.3336 –0.2721 –0.2009 –0.1209 –0.0357 0.0510 0.1350 0.2128 0.2815 0.3395 0.5000 | 0.1664 0.0615 0.0712 0.0800 0.0852 0.0867 0.0840 0.0778 0.0687 0.0580 0.1605 | 16.1408 5.9655 6.9064 7.7600 8.2644 8.4099 8.1480 7.5466 6.6639 5.6260 15.5685 | ||
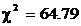 |
Исходя из приведенного расчета видно, что наиболее удачно приведенное распределение описывает нормальное распределение величины Х. Таким образом, окончательное уравнение имеет вид
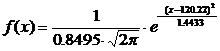
4. Поскольку распределение величины Х не является нормальным, но число опытов достаточно велико (n=97>30), мы воспользуемся приближенными формулами (73) и (74).
При подборе распределения величины Х значение рÎ[0.95, 0.975]. Исходя из этого, принимаем, что величина q=0.05. По табл. 7 приложения 3 значение аргумента 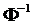
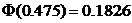
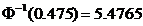

и с вероятностью »0.95 имеем 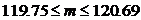
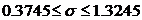
Пример 8
С помощью тестера (мультиметра), работающего в режиме измерения переменного напряжения, получено значение Uизм=120 В. Диапазон измерений прибора от 0 до 50 В. В паспорте указано, что при работе в этом диапазоне относительная погрешность 
1. Результат измерения обычно записывается в форме: Хд=Хизм+ 
Uд= Uизм+ 

где Uизм – измеренное значение (120 В); 

2. Абсолютная погрешность определяется из формулы:
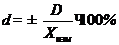
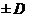
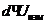
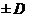
Ответ:Результат измерения записывается в виде U = (120,0 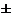

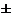
Пример 9
Для выполнения измерений применялось средство измерения с классом точности 2,5, со шкалой, проградуированной от 0 до 5 и ценой деления 0,2. Было получено значение величины A=3. Записать результат измерения.
1. Результат измерения записывается обычно в форме
Ад=Аизм 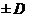

где Аизм – измеренное значение величины, 

Для решения задачи вспомним обозначение погрешностей через класс точности измерительного прибора.
2. Если класс точности обозначим 2,5, это означает, что приведенная погрешность 
Воспользуемся формулой приведенной погрешности:

где Ан – ширина диапазона измерений.
Из этой формулы следует, что
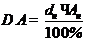
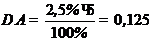
Относительная погрешность измерения рассчитывается по формуле:
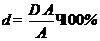

Ответ: Результат измерения запишем Ад=(3,000 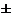

Число знаков после запятой в записи результата и погрешности должно быть одинаково.
Пример 10
Для выполнения измерений применялось средство измерения с классом точности 
Решение задачи осуществляется аналогично примеру 9.
1. Если класс точности обозначается 

Ответ: Результат измерения запишется как А=4,0 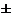

Пример 11
Для выполнения измерений применялось средство измерения с классом точности 2,5/1,0, со шкалой, проградуированной от 0 до 10 и ценой деления 0,2. Было получено значение величины A=6. Записать результат измерения.
1. Если класс точности обозначается 2,5/1,0, это значит, что указаны приведенные погрешности в конце и в начале диапазона измерений соответственно: 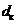
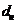
Для расчета относительной погрешности результата измерения 

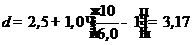
2. Рассчитываем абсолютную погрешность измерения
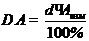

Ответ: Результат измерения запишется как А=6,00 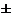

Если будем иметь данное не об одном, а о нескольких результатах наблюдения одной и той же величины, полученных с использованием одного и того же средства измерения, то следует с начала определить среднее арифметическое значение, которое и будет приниматься за измеренное значение.
Пример 12
Необходимо определить степень согласованности мнения пяти экспертов. Результаты мнения экспертов представлены следующим образом.
| №1 | — | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 |
| №2 | — | Q3 | Q1 | Q2 | Q5 | Q6 | Q7 | Q4 |
| №3 | — | Q1 | Q2 | Q5 | Q3 | Q6 | Q4 | Q7 |
| №4 | — | Q1 | Q3 | Q2 | Q5 | Q4 | Q6 | Q7 |
| №5 | — | Q3 | Q1 | Q5 | Q2 | Q6 | Q4 | Q7 |
Для решения используем формулу:
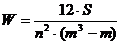
W – коэффициент конкордации;
S – сумма квадратов отклонений всех оценок рангов каждого объекта экспертизы от среднего значения;
n – число экспертов;
m – число объектов экспертизы.
0 2
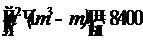
Ответ: Мнения экспертов достаточно согласованы.
Пример 13
Необходимо определить степень согласованности мнения девяти экспертов.
Результаты мнения экспертов представлены следующим образом.
Видео:Погрешности измеренияСкачать

Решение задач по метрологии
 Ответы на вопросы по заказу заданий по метрологии:
Ответы на вопросы по заказу заданий по метрологии:

- Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

- Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.

- Доработка бесплатна. Срок выполнения от 1 до 2 дней.

- Оценка стоимости бесплатна.

- Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

- Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.

- Присылайте в любое время! Я стараюсь быть всегда онлайн.
Содержание:
Основные термины, используемые в метрологии
Метрология — это наука об измерениях, методах и средствах обеспечения их единства и методах достижения необходимой точности.
Основные области метрологии включают в себя:
- общая теория измерений;
- единицы физических величин и их системы;
- методы и измерительные приборы;
- методы определения точности измерений;
- основы обеспечения единства измерений и единообразия средств измерений;
- эталонные и эталонные измерительные приборы;
- методы передачи размеров единиц от стандартных и примерных измерительных приборов к рабочим измерительным приборам.
Физическая величина — это свойство, которое присуще качественному отношению ко многим физическим объектам, но в количественном отношении индивидуально для каждого объекта. Измерение — это эмпирическое определение значения физической величины с использованием доступных технических средств, то есть процесс экспериментального сравнения данной физической величины с физической величиной с таким же названием, значение которой принимается за единицу.
Возможно, вас также заинтересует эта ссылка:
Единицей физической величины является физическая величина, которой по определению присваивается числовое значение, равное единице. Единство измерений — это состояние измерений, при котором их результаты выражены в юридических единицах, а ошибки измерений известны с заданной вероятностью.
Измерительные приборы — это технические средства, используемые для измерения и имеющие нормированные метрологические свойства. Измерительные приборы подразделяются на меры, измерительные приборы, измерительные преобразователи, измерительные приборы и вспомогательные измерительные приборы.
Мера — это измерительный инструмент, предназначенный для воспроизведения физических величин заданного размера.
Измерительное устройство — это измерительное устройство, предназначенное для формирования сигнала измерительной информации в форме, доступной для непосредственного наблюдения наблюдателем. Измерительные приборы могут быть: аналоговые, цифровые, индикационные и регистрирующие.
Измерительный преобразователь — это измерительный инструмент, предназначенный для генерации сигнала измерительной информации, удобный для передачи, дальнейшего преобразования, обработки и хранения, но не поддающийся непосредственному восприятию наблюдателем. Существуют различные типы преобразователей:
- — первичная — первая в измерительной цепи, измеренная величина подается на нее напрямую;
- — передача — служит для дистанционной передачи сигнала измерительной информации;
- — используется для изменения измеренного значения указанное количество раз.
Вспомогательные измерительные приборы — это измерительные приборы величин, которые влияют на метрологические свойства другого измерительного прибора при его применении. Измерительная установка представляет собой комбинацию функционально интегрированных измерительных приборов и вспомогательных устройств, предназначенных для генерации информационных сигналов измерений в форме, удобной для непосредственного наблюдения наблюдателем и расположенной в одном месте.
Измерительная система представляет собой комбинацию измерительных приборов и вспомогательных устройств, соединенных между собой каналами связи, предназначенную для генерирования измерительных информационных сигналов, удобных для прямой автоматической обработки, передачи и использования в системах автоматического управления.
1) Измерение — это измерительный инструмент для воспроизведения физической величины заданного размера. Меры: эталонные стандарты и рабочие.
Возможно, вас также заинтересует эта ссылка:
Основные единицы системы Cи:
- 1 л- [м] — длинный.
- 2 Т- [с] — время.
- 3 М- [кг] масс.
- 4 I- [A] ток.
- 5 т — температура [K].
- 6 J- [кг] — интенсивность света.
- 7 Н- [г / моль] — количество вещества.
2) Измерительный преобразователь — это измерительное устройство, предназначенное для преобразования одной физической величины в другую, которое используется для дальнейшего преобразования или передачи без непосредственного восприятия наблюдателя. Типы: электромеханический, термоэлектрический, выпрямительный, электромагнитный и др. 3) Измерительное устройство — это устройство, предназначенное для преобразования одной физической величины в другую в форме, удобной для непосредственного восприятия наблюдателя. Типы: электромеханический, электронный, цифровой. 4) Измерительные установки — это набор мер, собранных в одном месте или расположенных на одной панели. 5) Измерительные и информационные системы — это набор измерительных приборов и вспомогательных устройств, соединенных каналами связи.
Измеренное значение — это значение физической величины, полученное непосредственно из эксперимента в соответствии с показаниями устройства.
Результатом измерения является значение физической величины, полученное математической обработкой измеренных значений физической величины из известных функциональных соотношений. Принцип измерения — это совокупность физических явлений, лежащих в основе измерения физической величины. Метод измерения — это совокупность способов использования принципов и средств измерения.
Возможно, вас также заинтересует эта ссылка:
Решение задач. Теория погрешностей
Задача 1
Были произведены измерения некоторой физической величины. Было сделано 10 измерений. Определите доверительный интервал для оценки с надежностью Р истинного значения измеряемой величины, если известно, что результаты наблюдения подчиняются нормальному закону. Исходные данные представим в таблице 1. Таблица 1. Исходные данные
Определяем среднее арифметическое значение результатов измерения:
Определяем среднее квадратическое отклонение. Расчеты представим в виде таблицы 2.
Оценка среднего квадратического отклонения:
Число наблюдений 


Доверительная граница составит:
Доверительный интервал:
Т.е. с вероятностью 95% истинное значение величины находится в промежутке от 11,712 до 11,984
Возможно, вас также заинтересует эта ссылка:
Задача 2.
При проведении измерений различных физических величин были получены результаты (таблица 3). При помощи критерия Романовского проверить, являются ли указанные значения грубой погрешностью. Таблица 3. Исходные данные
Уровень значимости
Определяем среднее арифметическое значение результатов измерения:
Определяем среднее квадратическое отклонение. Расчеты представим в виде таблицы 4.
Оценка среднего квадратического отклонения:
По критерию Романовского при уровне значимости 

Вычисляем для наибольшего и наименьшего значения:
Следовательно, максимальное значение является грубым промахом, его нужно отбросить.
Возможно, вас также заинтересует эта ссылка:
Задача 3.
Определить, присутствует ли систематическая погрешность в ряду результатов наблюдений на заданном уровне значимости. Использовать критерий Аббе.
Определяем среднее арифметическое значение результатов измерения:
Представим результаты расчетов в виде таблицы 6.
Определяем дисперсию двумя способами:
По таблице критерия Аббе для всех уровней значимости при 

Средства измерений
Задача 4.
Для прибора с заданным классом точности рассчитать зависимость абсолютных погрешностей от результата измерений. Результаты представить в виде графика. Исходные данные Класс точности прибора — 0,4 Результаты измерения: 0; 100; 200; 400; 500; 600; 800; 1000 Ом
По способу маркировки класса точности средства измерения определяем, что его относительная погрешность 
где 
Расчетные данные представим в виде таблицы 7. Таблица 7. Результаты расчетов.
На рисунке 1 представим зависимость абсолютной погрешности от результата измерения.
Задача 5.
Для прибора указанного класса точности рассчитать значения абсолютных, относительных и приведенных погрешностей. Исходные данные Класс точности — 0,15 Результат измерения — 2В Диапазон — 0. 10В
По способу задания класса точности прибора определяем, что приведенная погрешность
=0,15%
Тогда абсолютная погрешность будет определяться: 
Возможно, вас также заинтересует эта ссылка:
Задача 6.
Для цифрового измерительного прибора рассчитать зависимость абсолютных и относительных основных погрешностей от результата измерений, результаты представить в виде таблицы и Исходные данные: Класс точности 0,25/0,1 диапазон -100. +100°С
Результаты измерений: 0; 10; 20; 40; 50; 60; 80; 100 °С
1. Определим относительную погрешность по формуле:


Результаты расчетов сведем в таблицу 8 Таблица 8. Результаты расчетов
Основы взаимозаменяемости
Задача 7.
Размеры деталей, которые изготовлены в цехах завода согласно заданным на чертеже номинальным размерам и предельным отклонениям были измерены. Из партии деталей измерили три штуки. Определить:
-годны ли измеренные детали; -для негодных деталей, если такие окажутся, установить вид брака: исправимы или неисправимый. -построить схему расположения полей допусков заданных размеров с указанием на ней предельных отклонений, предельных и действительных размеров.
Номинальный размер отверстия 



Определим наибольший предельный размер отверстия:
Наименьший предельный размер отверстия:
Определим годность измеренных деталей:
Условие годности выражается зависимостью:
Условие не выполняется, значит деталь является браком, брак является не исправимым, так как действительный размер отверстия превышает максимальный предельный размер отверстия -размер 18,043мм
Деталь является годной, так как действительный размер равен максимальному предельному значению -размер 18,000мм
Деталь является годной, так как действительный размер равен минимальному предельному значению отверстия
На рисунке 4 представим схему расположения поля допуска отверстия
Задача 8.
По известным номинальным размерам сопряжений и обозначению посадок изобразить схему расположения полей допусков посадок. В заданных соединениях определить:
-систему посадки; -предельные отклонения отверстия и вала; -допуски отверстия, вала и посадки; -предельные и средние зазоры и натяги; -предельные размеры вала и отверстия.
Номинальный диаметр сопряжения — 
Дана посадка
Данная посадка в системе отверстия, так как отверстие 


Определяем предельные размеры отверстия:
Вал
Определяем величину основного отклонения 

Определим предельные размеры вала:
Посадка 
На рисунке 5 представим схему расположения полей допусков посадки
Задача 9.
Для заданного эскиза вала известны номинальные размеры посадочных поверхностей под подшипники качения и предельные отклонения размеров. Вал будет вращаться в подшипниках качения класса точности 0.
Назначить: допуски круглости и продольного сечения посадочных поверхностей под подшипники качения;
-допуски перпендикулярности или торцового биения заплечиков подшипников качения. -допуск круглости и профиля продольного сечения посадочной поверхности под муфту и зубчатое колесо, учитывая, что степень точности зубчатого колеса по ГОСТ 1643-81-7D -величину шероховатости поверхностей, к которым устанавливаются допуски формы и взаимного расположения. Вычертить эскиз вала и проставить на нем допуски формы, взаимного расположения, шероховатость.
Размеры шпоночных пазов по ГОСТ 23360-78 Подшипник — шариковый радиально-упорный, класс точности — 0 Степень точности зубчатого колеса —7D.
Позиция 1. Допуск цилиндричности шейки вала под подшипники 
Позиция 3. Допуск соосности поверхности под подшипник качения принимаем 4мкм на 10мм ширины подшипника, ширина подшипника 14мм, тогда

Позиция 6. Допуск перпендикулярности заплечика вала принимаем 5мкм
Позиция 7. Допуск перпендикулярности торца под зубчатое колесо: Определяем необходимость назначения: 

Позиция 2. Допуск цилиндричности шейки вала под зубчатое колесо 
Позиция 4. Допуск соосности поверхности под зубчатое колесо, учитывая степень точности зубчатого колеса 7, принимаем
Позиция 5. Допуск соосности поверхности (выходной конец вала), учитывая степень точности изготовления 6, принимаем
Позиция 8. Допуск параллельности шпоночного паза, принимаем равным 

Для ступени вала под зубчатое колесо 
Допуск симметричности шпоночного паза, принимаем равным 

Для ступени вала под зубчатое колесо 
Назначаем шероховатость на поверхности вала, — шероховатость шеек вала под подшипники определяем по ГОСТ 3325-85 в зависимости от диаметра и степени точности подшипника. Для шейки вала
Шероховатость опорных торцев заплечиков вала составит 
-для поверхности 
Округляем полученное значение до стандартного:
На рисунке 6 представим эскиз вала.
Возможно, вас также заинтересует эта ссылка:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
🌟 Видео
Физические величины. Измерение физических величин | Физика 7 класс #3 | ИнфоурокСкачать

Виды измерений. Прямые, косвенные и совместные измерения. Часть 1.Скачать

Урок 4 (осн). Измерение физических величин. Цена деления шкалы измерительного прибораСкачать

01. Обработка результатов прямых измеренийСкачать

Точность и погрешность измеренийСкачать

Физика 7 класс (Урок№2 - Физические величины и их измерение. Измерение и точность измерения.)Скачать

Митин И. В. - Обработка результатов физического эксперимента - Измерение и Погрешность измеренийСкачать

Обработка результатов измерений. 2. Характеристики погрешностейСкачать

Урок 2. Точность физических величинСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Физические величиы Измерение физических величин Точность и погрешность измеренийСкачать

Физика-7. Фильм №79. - "Прямые и косвенные измерения физических величин"Скачать

Практика 10 Обработка результатов измеренийСкачать

Оценка неопределенности результатов измеренийСкачать


























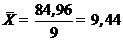

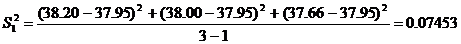
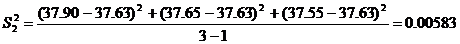
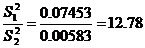
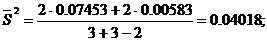
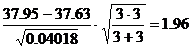
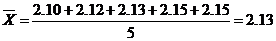
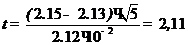
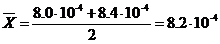

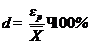
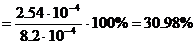
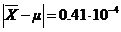

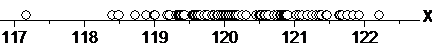
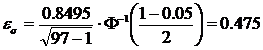
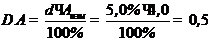

 Ответы на вопросы по заказу заданий по метрологии:
Ответы на вопросы по заказу заданий по метрологии:


























 =0,15%
=0,15%




































