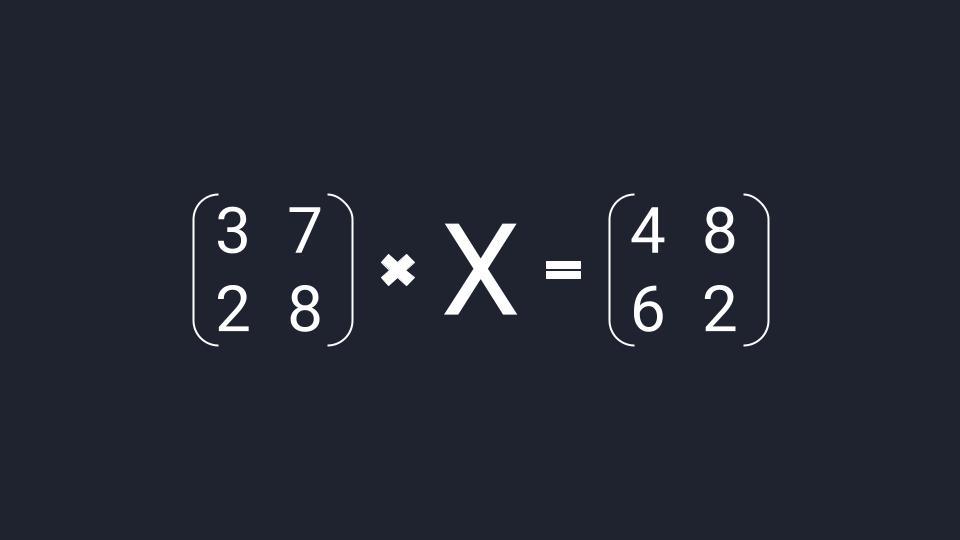Даны матрицы методами матричного исчисления найти неизвестную матрицу из уравнения (2 видео)

Решение матричных уравнений

Финальная глава саги.

Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».

Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.

Краткое содержание прошлых частей:

Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.

И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.

❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.

Содержание

Что такое матричное уравнение
Шаг 1. Упрощаем уравнение
Шаг 2. Вводим единичную матрицу
Шаг 3. Находим обратную матрицу
Шаг 4. Вычисляем неизвестную матрицу
Шаг 5. Проверяем уравнение
Ну и что
Онлайн калькулятор. Решение систем линейных уравнений. Матричный метод. Метод обратной матрицы.
Решить систему линейных уравнений матричным методом
Ввод данных в калькулятор для решения систем линейных уравнений матричным методом
Дополнительные возможности калькулятора для решения систем линейных уравнений матричным методом
Решение матричных уравнений: теория и примеры
Решение матричных уравнений: как это делается
Решение матричных уравнений: примеры
🌟 Видео

Видео:Матричное уравнениеСкачать

Что такое матричное уравнение

Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.

Видео:Решение матричных уравненийСкачать

Шаг 1. Упрощаем уравнение

Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.

Приводим матричное уравнение к упрощённому виду

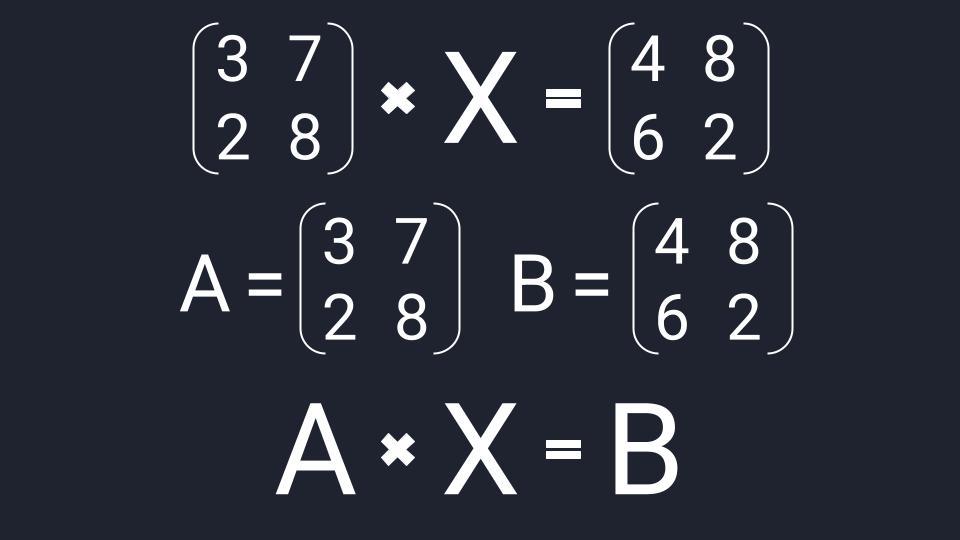
Видео:Матричный метод решения систем уравненийСкачать

Шаг 2. Вводим единичную матрицу

В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу.

Можно представить, что есть число 100 — это «сто в первой степени», 100 1

И есть число 0,01 — это «сто в минус первой степени», 100 -1

При перемножении этих двух чисел получится единица:
100 1 × 100 -1 = 100 × 0,01 = 1.

Вот такое, только в мире матриц.

Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А -1 . Неизвестную матрицу Х оставляем без изменений и переписываем уравнение:

А -1 × А × Х = А -1 × В

Добавляем единичную матрицу и упрощаем запись:

А -1 × А = E — единичная матрица

E × Х = А -1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем

Х = А -1 × В — новая запись уравнения

После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.

💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A -1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто.

Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Шаг 3. Находим обратную матрицу

Вспоминаем формулу и порядок расчёта обратной матрицы:

Делим единицу на определитель матрицы A.
Считаем транспонированную матрицу алгебраических дополнений.
Перемножаем значения и получаем нужную матрицу.

Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Третье действие: получаем обратную матрицу

Видео:Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Шаг 4. Вычисляем неизвестную матрицу

Нам остаётся посчитать матрицу X: умножаем обратную матрицу А -1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Решаем матричное уравнение и находим неизвестную матрицу X. Мы получили кратные числа и внесли дробь в матрицу

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Шаг 5. Проверяем уравнение

Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.

👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Проверяем ответ и получаем матрицу B — наши расчёты верны

Видео:§29 Решение матричного уравненияСкачать

Ну и что

Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:

Видео:Матричные уравнения Полный разбор трех типов матричных уравненийСкачать

Онлайн калькулятор. Решение систем линейных уравнений. Матричный метод. Метод обратной матрицы.

Используя этот онлайн калькулятор для решения систем линейных уравнений (СЛУ) матричным методом (методом обратной матрицы), вы сможете очень просто и быстро найти решение системы.

Воспользовавшись онлайн калькулятором для решения систем линейных уравнений матричным методом (методом обратной матрицы), вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на решения систем линейных уравнений, а также закрепить пройденный материал.

Видео:Решение системы уравнений методом обратной матрицы.Скачать

Решить систему линейных уравнений матричным методом

Изменить названия переменных в системе

Заполните систему линейных уравнений:

Ввод данных в калькулятор для решения систем линейных уравнений матричным методом

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Для изменения в уравнении знаков с «+» на «-» вводите отрицательные числа.
Если в уравнение отсутствует какая-то переменная, то в соответствующем поле ввода калькулятора введите ноль.
Если в уравнение перед переменной отсутствуют числа, то в соответствующем поле ввода калькулятора введите единицу.

Например, линейное уравнение x ₁ — 7 x ₂ — x ₄ = 2

будет вводится в калькулятор следующим образом:

Дополнительные возможности калькулятора для решения систем линейных уравнений матричным методом

Между полями для ввода можно перемещаться нажимая клавиши «влево», «вправо», «вверх» и «вниз» на клавиатуре.
Вместо x ₁, x ₂, . вы можете ввести свои названия переменных.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Видео:Обратная матрицаСкачать

Решение матричных уравнений: теория и примеры

Видео:§28 Матричные уравненияСкачать

Решение матричных уравнений: как это делается

Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,

где x — неизвестное.

А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.

Итак, матричным уравнением называется уравнение вида

где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.

Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу слева:

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому

Так как E — единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :

Как решить матричное уравнение во втором случае? Если дано уравнение

то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:

Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X . То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A .

Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение матричных уравнений: примеры

Пример 1. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :

Наконец, находим неизвестную матрицу:

Пример 2. Решить матричное уравнение

Пример 3. Решить матричное уравнение

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:

До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.

Пример 4. Решить матричное уравнение

Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:

Находим неизвестную матрицу:

Пример 5. Решить матричное уравнение

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:

Пример 6. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :